Categorie: Matematica
Tags: forme indeterminate funzione infinito limite zero
Scritto da: Vincenzo Zappalà
Commenti:40
3. Zero e infinito: le cose si complicano **
Proviamo ad affrontare operazioni un po’ più difficili, addirittura la moltiplicazione, la divisione e l’elevamento a potenza! No, non ridete. Quando si maneggiano numeri “strani” come infinito e zero le cose non sono mai semplici e regalano molte sorprese. Anzi ci porteranno davanti a un muro che ci obbligherà ad accettare un nuovo approccio.
Quanto vale 0∙0? Direi che non ci sono problemi ad arrivarci con facilità. La moltiplicazione è un’operazione che ci dice solo di addizionare un fattore a se stesso tante volte quanto indica l’altro fattore. Prendiamo allora 0 e addizioniamolo a se stesso … 0 volte. Ma che vuole dire tutto ciò? Semplicemente prendere zero e non fargli niente! Per cui
0 ∙ 0 = 0
Calcoliamo adesso l’espressione ∞ ∙ ∞.
Analogamente a prima, dobbiamo addizionare infinito a se stesso per infinite volte. Ossia: ∞ + ∞ + ∞ + ∞ + ecc., ecc, per un numero infinito di volte. No, non possiamo esagerare. Sappiamo già il risultato dato che la somma di due infiniti è ancora infinito. Oltre l’infinito non vi è nient'altro che infinito, se no che infinito sarebbe! Sommare 10, 50, 1000000 volte l’infinito continua a essere infinito. Ne deriviamo che:
∞ ∙ ∞ = ∞
Come casi generali di quanto detto sopra, potremmo scrivere che :
qualsiasi numero moltiplicato per zero dà come risultato zero. Beh, quasi sempre, teniamolo ben presente. Vale però anche ∞ ∙ 2 = ∞, ∞ ∙ 57 = ∞, ecc., ecc. In parole matematiche: qualsiasi numero moltiplicato per infinito deve dare infinito, tranne che ... Ci arriveremo fra pochissimo.
Prima di continuare con le moltiplicazioni è utile passare alle divisioni: fidatevi.
Proviamo con 0/0.
Sembra semplice ma non lo è. Sì, è vero, avevamo detto la volta scorsa che qualsiasi numero diviso per zero deve dare infinito. Ma non se il numero è proprio zero (ricordate che avevamo escluso questa possibilità). D'altra parte sappiamo anche che moltiplicare qualcosa per zero dovrebbe dare zero (ma non 1/0). Paragonare zero con se stesso è un bel problema e non si può certo concludere che faccia 1. Vi ricordate il discorso sui treni su due linee ferroviarie che vanno a diversa velocità? Ebbene, il ragionamento si ripete. Quali dei due arriva prima nel punto in cui le rotaie si incontrano (nel punto all’infinito)? Se vediamo i treni dal nostro punto di osservazione saremmo sicuri che il più veloce arriva prima dell’altro (uno sparisce all’orizzonte e l’altro no). Potremmo concludere che uno zero è più zero dell’altro, dato che viene raggiunto prima. Cosa vuol dire tutto ciò? Che se il treno più veloce è quello al numeratore la relazione 0/0 diventa uguale a zero, dato che quello al denominatore è già un numero piccolo, ma non piccolo come quello superiore. E come se la relazione diventasse 0/0.000000000001 che è , comunque, uguale a 0.
Se, invece, il treno più veloce fosse al denominatore, le cose si invertirebbero e otterremmo qualcosa del tipo 0.00000000000001/0 = ∞. Insomma, la soluzione non si può ottenere con le solite operazioni. Bisogna anche conoscere la velocità del treno! In altre parole, quale dei due treni si avvicina più velocemente allo zero. Al “limite” (mai vocabolo è stato scelto meglio!), potrebbero anche avere la stessa velocità e il risultato sarebbe uno. Non preoccupatevi, torneremo presto su questo concetto.
Cosa siamo costretti a dire? Ormai lo sappiamo (purtroppo): zero diviso zero ha una soluzione indeterminata. In altre parole, più esatte, possiamo anche dire che la forma 0/0 è indeterminata.
Le cose migliorano se facciamo ∞/∞ ? Nemmeno per sogno. Potrei dirvi che paragonare due infiniti pone lo stesso problema visto prima. Chi è più infinito dell’altro? Impariamo, però, a usare la poca matematica che abbiamo già imparato. Quante vale 1/∞? Beh, lo sappiamo già: è uguale a 0. Possiamo allora sostituire 1/∞ con 0. Su questo fatto non abbiamo dubbi. Scriviamo, allora:
∞/∞ = ∞ ∙ 1/∞ = ∞ ∙ 0
Beh, non abbiamo ottenuto molto di meglio, a prima vista. Tuttavia, possiamo continuare, dato che sappiamo anche (ma è la stessa cosa) che 1/0 = ∞. Sostituiamo ancora nella relazione di prima e troviamo:
∞/∞ = ∞ ∙ 0 = (1/0) ∙ 0 = 0/0.
Siamo ritornati al caso precedente, ossia alla forma 0/0. Ma questa è una forma indeterminata e di conseguenza lo è anche la forma ∞/∞.
E’ immediato dire che anche il prodotto tra zero e infinito è indeterminato. Infatti, guardando qualche riga sopra, abbiamo proprio scritto che ∞ ∙ 0 = 0/0. Accidenti, le cose diventano pesanti… Dobbiamo confessare che anche ∞ ∙ 0 è una forma indeterminata. Non ce ne va più bene una che sia una! Ecco perché prima avevo titubato a dire che qualsiasi numero moltiplicato zero dà come risultato zero. Qualsiasi numero tranne infinito! Idem per qualsiasi numero moltiplicato infinito: dà infinito solo se non è zero! E casi così ce ne sono parecchi...
Possiamo rifarci un po’, moltiplicando o dividendo un numero n qualsiasi per zero e infinito. Sì, sì, per loro è tutto facile, ma questo lo sapevamo già. Infatti:
n ∙ 0 = 0 e n ∙ ∞ = ∞.
Non avrei nemmeno bisogno di spiegarlo, ma è come se sommassi n volte 0 e ∞. Le loro somme valgono 0 e ∞, rispettivamente (andate a vedere cosa avevamo concluso nelle addizioni).
Continuiamo: n/0 = ∞ e n/∞ = 0. Anche questo lo avevamo già stabilito fin dall’inizio dell’articolo scorso e ribadito poco fa. Meno male, qualcosa sta funzionando.
Concludiamo con qualche altra divisione:
0/∞ e ∞/0. Non dovreste avere problemi a trovare da soli la soluzione, anche in modo “matematico” e non concettuale. Ormai sapete come fare: basta sostituire ∞ con 1/0 e la prima espressione si trasforma in 0 ∙ 0 che sappiamo essere uguale a 0. Nella seconda sostituiamo 0 con 1/∞ e troviamo ∞ ∙ ∞ = ∞. Tutto bene, insomma; le soluzioni sono alla nostra portata.
Probabilmente vi sto riempiendo la testa di zeri e di infiniti. E’ meglio fermarsi un attimo e ricapitolare quanto abbiamo trovato nella moltiplicazione e nella divisione (se dimentico qualcosa fatemelo presente…).
1/∞ = 0
1/0 = ∞
0 ∙ 0 = 0
∞ ∙ ∞ = ∞
0/∞ = 0
∞/0 = ∞
0/0 indeterminata
∞/∞ indeterminata
∞ ∙ 0 indeterminata
n ∙ 0 = 0
n ∙ ∞ = ∞
n/∞ = 0
∞/n = ∞
0/n = 0
n/0 = ∞
E se volessimo passare a espressioni esponenziali, del tipo ab ? Proviamoci, cercando di ricordare le proprietà delle potenze… (per adesso prendiamole per buone, tra un paio di articoli ci torneremo sopra). In particolare, ricordiamo che elevare a potenza vuol solo dire moltiplicare la base a per se stessa tante volte quante dice l’esponente b. Se a fosse uguale a 3 e b uguale a 5 (ossia 35) significherebbe fare 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 .
Vi dico subito che le cose si complicano un po’. Potrei darvi i risultati senza tante spiegazioni. Ma andrei contro il senso di tutti questi discorsi che cominciano a sembrare privi di senso (meno male che la MQ ci ha abituati alle cose illogiche…). Proviamo e poi magari mi chiederete ulteriori chiarimenti senza alcun timore.
Cominciamo con 00 . La soluzione sembrerebbe banale dato che sappiamo che un numero elevato a zero fa sempre uno. Perché? Beh, questa è una specie di convenzione che si è scelta non avendo praticamente senso concreto moltiplicare un numero per se stesso zero volte. Si scrive perciò n0 = 1. Tuttavia, sappiamo anche che 0 moltiplicato per se stesso n volte fa sempre zero, ossia 05 = 0 ∙ 0 ∙ 0 ∙ 0 ∙ 0 = 0. Siamo di fronte a un dilemma.
0 è un numero, ma a seconda che lo consideriamo tale nella base o nell’esponente il risultato è diverso. Potremmo concludere facilmente che la forma è indeterminata perché non sappiamo proprio come trattarla. (Attenzione, non confondiamola con 0 ∙ 0. In questo caso è come dire 02 e questa vale senz’altro 0). Potremmo, però, anche arrivarci in modo puramente matematico.
Seguitemi attentamente… dire 0 vuole anche dire 1 – 1: non vi sono dubbi. La relazione diventa allora 0(1-1) . Una proprietà delle potenze ci dice però che a(b-c) = ab/ac. Vi sembra una cosa strana e nuova? No, no. Pensate al rapporto a6/a2. E’ vero o no che si può semplificare dividendo sopra e sotto per a2? Direi proprio di sì e il risultato diventa a4. In altre parole, non ho fatto altro che fare a6/a2 = a(6-2) = a4. Torniamo allora alla nostra relazione 00.
00 = 0(1-1) = 01/01 = 0/0
Fermi tutti! Questa è una relazione che conosciamo molto bene e sappiamo che è indeterminata. Lo sarà, quindi, anche 00.
E se facessimo ∞0 ? Le cose cambierebbero di poco, dato che potremmo usare lo stesso sistema:
∞0 = ∞(1-1) = ∞1/∞1 = ∞/∞
Ma anche questa la conosciamo bene ed è una forma indeterminata.
Più semplici e immediate sono invece le soluzioni delle relazioni 0∞ e ∞∞. In questo caso l’elevazione a potenza ci dice solo che dobbiamo prendere 0 e moltiplicarlo per se stesso infinite volte. Nessun problema. Sappiamo benissimo che moltiplicare zero per se stesso, quante volte vogliamo, resta sempre 0. Così come moltiplicare infinito per se stesso infinite volte vale sempre infinito.
Non vi sono nemmeno problemi a fare ∞n e n∞ (con n maggiore di 1… vedremo tra poco perché…).
Entrambi danno ∞. E’ ovvio: moltiplicare infinito n volte per se stesso è ovviamente infinito. Moltiplicare un numero n, maggiore di 1, infinite volte per se stesso non può che essere infinito.
Tuttavia, nel secondo caso, se il numero n è più piccolo di 1, le cose cambiano … Accidenti questo non ce lo saremmo aspettati. Proviamo a vedere perché.
Se n è più piccolo di uno, può esprimersi sempre come una frazione del tipo m/M, dove M > m. Riscriviamo allora la nostra relazione n∞ come (m/M)∞ = m∞/M∞. Questa forma sembrerebbe dirci che siamo ricaduti nel caso ∞/∞. E qui casca l’asino! Ossia, caschiamo tutti veramente!
Devo ammettere di avere lasciato questo caso per ultimo proprio perché ci mette veramente di fronte a un problema che abbiamo finora solo sfiorato, senza avere il coraggio di affrontarlo, tentando di risolvere (o non risolvere) le varie espressioni con le operazioni della matematica più elementare, alla portata di tutti. Adesso, non possiamo più nascondere la polvere sotto al tappeto e dire che la forma è indeterminata.
Ripensiamo ai treni che viaggiano a velocità diverse verso il punto all’infinito. Ebbene, se la base della potenza è più grande di un'altra, vuol dire che il treno fa prima ad arrivare all’infinito e quindi M∞ arriva a infinito prima di m∞. Dobbiamo accettare il fatto (già accennato) che l’infinito al denominatore è più infinito di quello al numeratore e quindi il risultato vale 0, come se fossimo nel caso 1000000000000/∞, già trattato precedentemente.
No, non possiamo più accontentarci di parlare di treni più o meno veloci. Dobbiamo veramente imparare qualche nuova operazione per lavorare a nostro agio con 0 e ∞. Anche perché l’ultimo caso trattato ci porta a una situazione estremamente ambigua che forse vi è sfuggita. La ribadisco:
n∞ ha una doppia soluzione. Se n > 1 vale ∞; se n < 1 vale 0.
E se n fosse proprio 1. Non potremmo rispondere e saremmo veramente imbarazzati. Non ci resta che concludere che anche 1∞ è una forma indeterminata, proprio perché è al bordo (al limite…) di due soluzioni opposte.
Sono senza parole, scusate…
Ricapitoliamo gli ultimi risultati e poi passiamo alla discussione finale.
00 indeterminata
∞0 indeterminata
0∞ = 0
∞∞ = ∞
0n = 0
n0 = 1
∞n = ∞
n∞ = ∞ ( se n > 1)
n∞ = 0 ( se n < 1)
1∞ indeterminata
Abbiamo tentato di andare avanti con le operazioni più semplici, ma, alla fine ci siamo trovati di fronte a un muro.
Che dirvi? Mi ero illuso, inutilmente, di trattare due numeri speciali come ∞ e 0 al pari di due numeri qualsiasi. A volte ci sono riuscito, a volte ho usato la frase (anzi la scappatoia) “forma indeterminata”, ma alla fine la situazione “un numero elevato a infinito” mi ha bloccato la strada e mi ha convinto di avere sbagliato tutto.
No, non mi picchiate. In realtà l’ho fatto apposta! Lavorando in questo modo abbiamo sentito un po’ alla volta la necessità di introdurre un nuovo tipo di operazione. Un’operazione che diventa essenziale quando si parla di infinito e di zero, ma che è utilissima e fondamentale anche in altri casi meno eclatanti.
Se vi avessi introdotto subito questa operazione, qualcuno avrebbe potuto dite: “Le solite farneticazioni matematiche. Sempre a cercare di rendere difficili le cose semplici. A cosa potrà mai servire introdurre una nuova operazione? Solo a complicare le cose e a divertirsi con i numeri, senza un bisogno veramente pratico”. Ebbene, ho provato a camminare lungo le rotaie con le normali operazioni che tutti conoscono e vi ho mostrato che ci scontriamo con difficoltà insuperabili. E’ quindi necessario fare un passo in più. Necessario proprio per rendere concrete soluzioni che non riusciamo a trovare.
Questa nuova operazione non è altro che il passaggio al limite. ossia avvicinarsi a un valore numerico, compresi zero e infinito, studiando il modo con cui lo fa. Chiamatela pure “velocità con cui il treno viaggia sulle rotaie”, l’ importante è che ci servirà a stabilire una gerarchia tra gli zeri e gli infiniti. Anche loro non sono tutti uguali! Invece di usare la frase “uguale a”, impareremo a usare la più generale frase “tende a”.
Prima, però, è opportuno saltare di palo in frasca e iniziare a parlare di funzioni matematiche. Perché? Proprio adesso che si poteva iniziare a risolvere le forme indeterminate? Ebbene sì. Le funzioni matematiche sono proprio quelle cose che ci permettono di sapere con che velocità ci stiamo avvicinando a certi valori numerici. Sono proprio i treni che potremo prendere di volta in volta.
Solo conoscendo loro potremo risolvere le forme indeterminate. O, in altre parole, loro sono i casi pratici che portano alle situazioni indeterminate (ma anche determinate) che abbiamo visto in questi tre articoli introduttivi. Parlare di funzioni, vuol dire dare una veste pratica e concreta alle formule matematiche. Oltretutto ci permettono di vedere continuamente un’espressione matematica sotto la sua veste geometrica, molto più comprensibile e immediata.
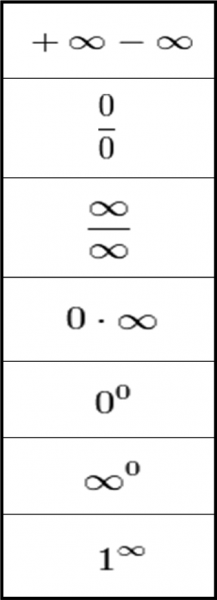
Concludo con una tabella riepilogativa dei “magnifici sette”, ossia i sette casi che abbiano definito come indeterminati. Li risolveremo tutti, anche se qualcuno ha poco interesse pratico (soprattutto nella fisica) e necessita di funzioni veramente astruse e ben poco note.
Vi consiglio di rileggere questi primi tre capitoli con attenzione. Cercate di capire i concetti affrontati. E’ inutile cercare di imparare a memoria i risultati. Sono serviti solo ad arrivare al nocciolo del problema. Potete sempre riferirvi alla tabella finale. Se avete digerito la logica dei vari passaggi, potrete sempre ricavarveli da soli. Questa è la VERA matematica. La memoria serve a poco… per la tabellina pitagorica e poco di più. Se le si dà la mano e si capisce il suo metodo di ragionare, la memoria è quasi inutile. Ogni soluzione è sempre deducibile attraverso i concetti base. Cercate di seguire questa strada e vedrete che farete vostra la sua bellezza sintetica e la sua logica quasi artistica.
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica
40 commenti
Enzo, non riesco a capire perché 1 elevato alla infinito sia indeterminato, ragionandoci sopra la mia testa bacata mi dice che dovrebbe essere sempre 1......cosa mi manca per capire il perché, invece, sia indeterminato?
Grazie per l'articolo!
caro Andrea,
rileggi bene quanto scritto a riguardo. Esso deve essere considerato indeterminato perché si è visto che per n>1 si ottiene un certo risultato, mentre per n < 1 il risultato va verso l'opposto. In questo caso, non si può dire niente di cosa faccia quando n è proprio al limite dei due casi (non è né maggiore né minor di 1, ma è proprio 1). E' una forma indeterminata perché n** infinito ha valori diversi a seconda se n> 1 o n<1. Non sappiamo cosa concludere per n=1... Tutto lì... Comunque, la forma (1** infinito) è una forma che non troveremo mai, dato che abbisogna di funzioni troppo complicate per noi...
ottimo articolo, i limiti e le derivazioni mi sono sempre piaciuti
Strabiliante leggerti Enzo, la matematica scorre come un romanzo qualunque.
Grazie Enzo.
A proposito non è che ti richiamano ad insegnare visto i personaggi (Professori) che spesso si ritrovano oggi i nostri ragazzi. Farebbero bene , mas noi non ti vogliamo perdere.
ti prego Mario... se continui così quasi quasi ci credo!!!
un articolo veramente bello, e' stata una trattazione molto "sensibile" nei confronti di chi non ha molte basi matematiche...
ho capito quasi tutto pure io!
un dubbio che mi e' rimasto e' lo stesso di andrea: 1 alla n = indeterminato. Ho capito il concetto che 1 in tal caso londevo considerare come spartiacqua tra il caso di n<1 e n>1 pero' sinceramente da ignorante non mi sarei fatto problemi a determinare il risultato uguale a 1, mi sarebbe bastato considerarlo come elemento perfettamente a meta' tra il tendere a zero e il tendere all'infinito, in pratica come l'inizio della discesa verso il basso o l'inizio della salita verso l'alto.
MI sarebbe venutk quasi da paragonarlo all'orizzonte degli eventi ma mi rimetto alla potenza della matematica in merito e lo prendo come postulato!
ciao ragazzi.
Anche io non riesco a capirlo questo 1 all' infinito.
nella mia testolina mi viene da pensare che 1 lo posso moltiplicare quante volte mi pare per se stesso e farà sempre 1.
3 elevato alla 5 è : 3x3x3x3x3
1 alla inf. io lo vedo come:
1x1x1x1x1x1.....cioè se continuo in eterno non vedo come io possa trovare un risultato diverso da 1.
Non mi entra in testa questa cosa.
Ciao a tutti.
Grazie Enzo, stimoli sempre il pensiero!
cari amici,
l'ovvietà del risultato (apparente) introduce perfettamente nella necessità di utilizzare un'operazione di tipo diverso. Dobbiamo pensare che, malgrado abbiamo fatto di tutto, l'infinito resta un punto veramente speciale e pieno di sorprese. Ce lo dice proprio il fatto che se n è minore di uno, n**inf va a zero e non a infinito. Mentre se n è maggiore di zero si va tranquillamente verso la "logica", ossia infinito. Cosa capita quando si è vicini a n = uno? Se ci avviciniamo venendo da n<1 continuiamo, comunque, a vedere lo zero, che possiamo immaginare come un buco profondissimo. Come avvicinarsi a una scogliera profonda. Chiudiamo gli occhi e portiamoci a n appena più grande di 1, Riaprendoli ci troviamo immediatamente in un deserto senza fine. Come abbiamo fatto a passare da una voragine a un deserto piatto e senza limiti? Deve essere successo qualcosa quando n = 1. Per scoprirlo dobbiamo proprio prendere una macchina speciale e avvicinarsi lentissimamente sia dalla sua sinistra che dalla sua destra. Alla fine, scopriremo cosa capita realmente, ma non possiamo certo dirlo senza agire in questo modo. Risulta quasi banale il bisogno di introdurre il limite e non solo il limite da una sola parte, ma sia da destra che da sinistra. L'infinito, con tutti i suoi problemi, mi è servito per far capire la necessità di questa nuova operazione. Vedremo tra poco, che per i punti qualsiasi sembra veramente inutile, ma per certi punti è invece essenziale!!! Potrei dirvi che n**inf è un qualcosa che ha un punto di discontinuità al variare di n? Forse è troppo presto, ma...
Abbiate fede. Il prossimo articolo torna a quanto di più banale ci possa essere... tanto ormai il problema che troveremo si è già fatto sentire. Ormai abbiamo le spalle robuste!!!
Comunque, grazie per riflettere e pensare a cose che normalmente non interessano a nessuno!!! Mi raccomando, divulgate anche voi!!!!
Io ci ho ragionato sopra un po' e sono giunto alla conclusione che 1*inf é indeterminato perché non sappiamo quanto valga in termini assoluti l'inf. Possiamo solo quantificare un "tende a", e questo valore non é detto che corrisponda a un numero intero......sbaglio?
caro Andrea...
temo che non sia proprio giusto quello che pensi (devo ammettere che non l'ho capito molto bene...). Hai ragione a dire che infinito resta un concetto vago, ma il vero problema è che abbiamo cercato finora di dargli un valore ben determinato. In realtà, esso indica solo un qualcosa che non si raggiunge mai, un simbolo per riassumere un'idea, anche se reale. Può darsi che diciamo la stessa cosa... non so. Possiamo, per adesso, solo dire che quando ci si avvicina a questo concetto non tutte le operazioni possono essere fattibili. Il concetto di limite (che devo ancora introdurre... attenzione!) servirà proprio a trattare un concetto vago e non quantificabile come fosse qualcosa che acquista un senso logico. Le forme indeterminate, come 1 ** inf (che è la meno comprensibile), avranno proprio bisogno dei limiti per essere risolte.
Stai rischiando di correre troppo avanti e non aspettare che le cose vengano spiegate un po' alla volta. Per adesso, ti consiglio di considerare le forme indeterminate come incidenti di percorso, come muri che non riusciamo ancora a superare. Non cercare di capirne la vera essenza che avrà bisogno di altri concetti come la funzione e, appunto, il limite. Tra un po' vedrai che torneremo su tutte le forme in cui compaiono 0 e infinito e le tratteremo in modo più matematico e meno empirico. I primi tre capitoli li ho solo introdotti per acquistare un po' di dimestichezza con certi problemi di linguaggio non ancora matematico, ma solo fisico...
Il vero problema è che se n < 1 l'espressione può essere scritta come (1/m)**inf, dove m=1/n. ma m elevato infinito vale infinito e, quindi, 1/infinito vale 0, senza problemi. Se invece n>1 hai una forma n**inf. che vale sicuramente infinito. Pur andando vicinissimo a 1, da un lato ottieni zero e dall'altro infinito. Il punto 1.000000 ...... 00000, comunque tu riesca a scriverlo, o cade da una parte o cade dall'altra. Non è proprio possibile dire quello che potrebbe valere in un punto 1 che non potrebbe mai essere esatto fino all'ultima cifra decimale. L'uno perfetto non è materialmente possibile e quindi abbiamo sempre o un valore zero o infinito pur andandogli vicinissimo da un lato o dal'altro. Niente da fare: abbiamo proprio bisogno di cambiare approccio e introdurre il limite.... ma non ci siamo ancora arrivati...
Abbi pazienza....
Credo di avere capito, dobbiamo insomma evitare di ragionare in termini di "assoluto" e affrontare di petto il concetto di "valore il piú possibile approssimato a quello che vogliamo rappresentare"......mi puzza un po' di MQ
Ok cerco di non correre troppo, e chiedo scusa....ma quando mi fisso su una cosa che non comprendo, questa diventa un assillo per me 
nessuna scusa Andrea,
quando si ha voglia di ragionare si è sempre nel giusto!!!! Spero solo di rispondere ai tuoi dubbi quanto prima, ma non posso infilare lezioni troppo ravvicinate...
grazie mille per l'ultima spiegazione chiarissima! ho capito anche io ora!
Ciao ragazzi.
Ho letto che esistono casi in cui 1^inf=1.
Peccato che ho lascito le membra sul pc quando è entrato Nepero.
Bisogna aspettare i limiti notevoli da quanto ho capito e dovrebbe entrare in questo discorso il numero "e" , o lameno è cià che mi pare di aver capito.
Quanto è brutto essere ignoranti e non sapere le cose. :/
Ciao.
Andrea.
Io invece andrea lo trovo bellissimo!
Ogni giorno é una sorpresa e imparo qualcosa di nuovo...Beata ignoranza, se sapessimo gia tutto sai che noia? Penso che anche vivere avrebbe poco senso 
(ok basta con il filosofico, che oggi non piove e non siamo davanti a una bottiglia di vino eheheh). Nepero l'ho incontrato di recente mentre facevo ricerche su 1*inf....ma mi pare che al momento sia decisamente un passo piú lungo della gamba....e forse anche di tutte e due le gambe assieme 
cari amici,
Nepero e soprattutto il numero "e" lo troveremo di sicuro...ah se lo troveremo!!!! Non sperate di lasciarlo indietro. Però diamo tempo al tempo... e anche la motivazione di 1^inf sarà compresa (è proprio un caso particolare, però che con la fisica ha poco da spartire)...
Ciao Enzo,
per le operazioni di moltiplicazione è tutto piuttosto chiaro, non sono affatto diverse dalle addizioni, su questo non ho avuto alcun problema.
Per le operazioni di divisione tra 0 e ∞ vorrei essere sicura di aver capito bene prima di passare alle potenze:
· se abbiamo un’ operazione dove al numeratore abbiamo 1 o n il risultato di questa è l’inverso dl denominatore; (n/0= ∞ ; 1/∞=0)
· se abbiamo un’ operazione dove al numeratore abbiamo 0 o infinito il risultato di questa è uguale al numeratore.(0/n=0 ; ∞/n=∞)
Spero di non aver semplificato troppo ma avendo in mente questo concetto riesco facilmente a risolvere le operazioni . Però per le forme indeterminate sono ancora costretta ad impararle a memoria perché non riesco a capirle. 0/0, ∞/∞, 0*∞ sono forme indeterminate perché moltiplicare o dividere tra di loro queste due grandezze non ha senso oppure perché il punto zero è solo relativo e non è uguale a ∞?
Aiuto
Giorgia
Dunque Giorgia. Il fatto che n/inf sia zero e che n/0 = inf, deriva dal discorso fatto all'inizio. A parità di numero al numeratore (finito) più aumenta il denominatore più il rapporto diventa piccolo, ossia tende a zero. Mentre più il denominatore diventa piccolo e più il rapporto diventa grande e quindi il risultato tende a diventare infinito.
Quindi è facile dire che n/inf = 0 e che n/0 = inf
Se il numero (finito ) è al denominatore succede il contrario. Più il numeratore cresce e più il rapporto diventa grande e quindi si ottiene inf. Più il numeratore diventa piccolo e più il rapporto diventa piccolo e quindi il risultato tende a diventare zero.
Quindi 0/n = 0 e inf/n = 0
La tua regoletta funziona, ma la motivazione deve essere compresa caso per caso, facendo -se necessario- proprio dei casi pratici. Metti n = 5 e poi comincia a scendere col denominatore , prima 1, poi, 0.00001 e poi 0.0000000001 e ti accorgerai che il risultato diventa sempre più grande. E così in tutti i casi.
Compreso questo punto, il resto viene di conseguenza. Se questi risultati valgono per qualsiasi numero finito devono valere anche per n = 1 e infatti:
1/inf = 0
1/inf = inf
0/1 = 0
inf/1 = inf
Se invece provi a prendere due numeri piccolissimi, uno lo metti al numeratore e uno al denominatore continui ad avere un numero abbastanza grande. Per esempio
0.000001/0.000002 = 1/2, ma anche 0.00000000001/0.00000000002 = 1/2. Ossia, anche se i numeri diventano piccolissimi il loro rapporto rimane lo stesso e potrebbe anche rimanere così per sempre. Come facciamo per decidere? Dobbiamo vedere se aumenta di più al passare del tempo (o di quello che preferisci) quello di sotto o quello di sopra. Se aumenta di più quello di sopra prima o poi il risultato del rapporto diventa molto grande e tende, quindi, a infinito. Se aumenta di più quello di sotto il risultato del rapporto diventa sempre più piccolo, ossia tende a zero. In entrambi i casi, però i due numeri sopra e sotto tendono a diventare sempre più piccoli (ossia tendono a zero entrambi), ma uno vince rispetto all'altro.
Non potendo saperlo dalla semplice scrittura 0/0 dobbiamo limitarci a dire che è una forma indeterminata.
Se è indeterminata la forma 0/0 deve esserlo anche la inf/inf. Ci puoi arrivare con lo stesso ragionamento di prima (invertendo le condizioni) oppure dicendo semplicemente che, sapendo che 1/inf = 0 e 1/0 =inf, cose che sappiamo già da prima). facendo un po' di sostituzioni ottieni proprio che
inf/inf = 0/0 (basta dire che il num. può essere scritto come 1/inf e così anche il den. ). Ma dato che 0/0 era indeterminata lo deve essere anche inf/inf che è esattamente la stessa cosa.
tale e quale per 0 per inf.; basta dire che inf = 1/0 e sostituire. Si ottiene subito:
0 per inf = 0/0 , ma questa sappiamo già che è indeterminata!
Spero di averti chiarito i dubbi e si non aver fatto più confusione. Prima di andare avanti vorrei che tutti gli interessati abbiano risolto i dubbi....
????
Quindi anche chi non è mai intervenuto, ma ha dei dubbi si faccia vivo!!! Senza paura se no c'è il rischio che poi le cose si complichino...
OK
Grazie Enzo, sei stato chiarissimo
non è poi così difficile...
Ho fatto vari esempi come mi hai suggerito :
Se nell'operazione n/0=inf sostituiamo con numeri reali abbiamo 5/0.000001= 5.000.000 . Effettivamente basta porsi la domanda "Quante volte il denominatore sta nel numeratore?". Ovviamente più il denominatore è piccolo, più grande sarà il risultato e quindi tendente all'infinito... (non riporto tutti gli esempi per motivi si spazio e per non annoiare)
Tante volte ci si spaventa subito quando si incontrano strani simboli...
Grazie mille
Giorgia
ps: penso comunque che avrò ancora bisogno di aiuto per il passo successivo, adesso farò mie queste informazioni e poi passerò al livello successivo...
Ottimo Giorgia!!!! :-
Aspetto le tue domande....
Ciao Enzo,
ho affrontato il passo delle espressioni esponenziali e mi è tutto chiaro (stranamente). L'unico dubbio che ho riguarda l'operazione di 1 elevato ad infinito. Mi faresti un esempio numerico per aiutarmi a capire? Tu dici che è indeterminata perchè è al limite di due soluzioni ma per me 1 moltiplicato infinite volte per se stesso fa sempre 1.
Grazie
Giorgia
cara Giorgia,
prova a leggere la risposta che ho dato ad Andrea, che aveva il tuo stesso dubbio. A lui è servita... Se non basta, torniamoci su...
Ok Enzo,
adesso ho capito...
Grazie mille
Volevo intervenire però e per fortuna ho letto l'articolo quando erano stati scritti un mare di commenti ed un mare semplici ed esaurienti risposte. Quindi fino a qui ho capito.
Grazie
ottimo Gianluca!!!!
Sig. Vincenzo, io non pongo nessuna domanda
, in quanto a furia di leggere e rileggere l'articolo, diciamo che per una volta ho quasi capito qualcosa....... comunque aspetto con ansia il prossimo articolo e poi spero di fare anch'io domande sensate 
......
P.s.: quando ha introdotto il termine " tende a ", si riferiva per caso agli asintoti di una funzione???
caro Antonio (mi raccomando il TU),
il termine tende a non si riferisce solo agli asintoti, ma alla definizione stessa di limite di una funzione. Proprio quella che darò tra poco... Si può tendere a infinito anche senza che vi sia un asintoto... pensa alla retta...Non corriamo, comunque....
Ti ringrazio per il "tu"
....
Grande Enzo, ti stimo molto
grazie iotutto!!!
Il paradosso dell’eternità della vita: “Se anziché contare il tempo che ho in anni, mesi e giorni, io lo conto in miliardesimi di miliardesimi di miliardesimi di secondo, risulta che ho un numero di istanti di vita così grande da tendere a infinito; e poiché non ho alcuna predisposizione a schiattare (quest’anno ho fatto anche l'antinfluenzale) posso ritenere di essere pressoché immortale ?! Con sommo gaudio.”
E' un fesseria, o effettivamente un paradosso
Ciao Elio e benvenuto!
Ciò che dici mi ha fatto tornare in mente questo racconto di Mauritius, spero che ti piaccia...
"Cristalli di tempo"
caro Elio,
tu dici: se aumento il numero di intervalli faccio tendere il loro numero a infinito. Sì, ma, contemporaneamente, fai anche tendere l'intervallo di tempo a zero. Se non fosse zero, il numero non sarebbe infinito... ma allora ottien una forma zero per infinito... Mi spiace, ma dobbiamo far buon viso a cattivo gioco...iol tempo, per adesso, non si riesce a fregare...
errore gravissimo il tuo!! non si può usare la regola della divisione di potenze quando la base è zero !
se tu scrivi :
00 = 0(1-1) = 01/01 = 0/0
allora varrebbe pure : 0 = 0^3 = 0(6-3) = 0^6/0^3= 0/0
cosa palesemente falsa !
riscrivo perchè ha perso la formattazione:
errore gravissimo il tuo!! non si può usare la regola della divisione di potenze quando la base è zero !
se tu scrivi :
0^0 = 0^(1-1) = 0^1/0^1 = 0/0
allora varrebbe pure : 0 = 0^3 = 0(6-3) = 0^6/0^3= 0/0
cosa palesemente falsa !
caro Pino,
ma l'hai letto l'articolo ???? Temo di no...
Ciao Enzo, scusa innanzitutto se ho letto l'articolo dopo 10 anni dalla sua uscita.
Ciò premesso, da appassionato incompetente quale io sono, non sono d'accordo che l'1 perfetto non è materialmente possibile: esso esiste benissimo come esistono tutti gli altri numeri naturali, ciò sul piano prettamente matematico; ho visto che tu dici testualmente che l'1 perfetto non è materialmente possibile, laddove forse intendi nel mondo della fisica, ma sul piano matematico, a mio modestissimo avviso, le cose dovrebbero stare così:
1) 1^°° = 1 x 1 x 1......infinite volte=1 (quindi nessuna forma indeterminata)
2) lim n^°° per n-->1 questo sì che è una forma indeterminata, che dà come risultato zero oppure infinito a seconda che si tenda a 1 rispettivamente da valori (positivi) inferiori o superiori a 1 (ovviamente nel caso di numeri negativi si guarderà al valore assoluto per decidere se il risultato sarà zero oppure - infinito).
Che ti sembra?
Marco
caro Marco,
non devi mischiare un valore ben determinato con un valore espresso come limite. 1^inf può giustamente essere scritto come 1 x 1 x 1x 1... e valere sempre uno. Ma se facessi lo stesso con il numero 2? 2 x 2x 2 x2 x... varrebbe infinito, così come per tutti gli altri numeri. Già questa situazione rende il numero 1 molto speciale. Moltiplicarlo infinite volte per se stesso non cambia il risultato: 1^2 = 1^5 = 1^n = 1. Non è quindi così ovvio accettare il risultato. Se poi aggiungiamo che 0.99999 ^ inf = zero e 1.0000001 ^ inf = inf, la peculiarità di 1 è manifesta. Non per niente tu dici che basta passare al limite e sono pienamente d'accordo, ma ciò rende 1^inf una forma indeterminata, perché tutto dipende da come ci si arriva. Quindi, del tutto simile a inf/inf e 0/0.
Spero di essere stato chiaro...
Chiarissimo Enzo, grazie.
E pensandoci bene, circa i numeri 0 e 1:
sono gli unici numeri che rispettivamente moltiplicato per infinito il primo ed elevato ad infinito il secondo costituiscono forme indeterminate
e al tempo stesso sono gli unici ad avere in comune il fatto che moltiplicati per se stessi danno sempre se stessi (0 x 0 = 0, 1 x 1 = 1).
Che coincidenza strana e... che bella.
Marco
grazie a te Marco!