Categorie: Fisica classica Meccanica quantistica
Tags: elettrone fotone meccanica quantistica particelle scattering Compton urto a due dimensioni
Scritto da: Vincenzo Zappalà
Commenti:15
9. Dal biliardo all’effetto Compton (seconda parte) ***
Questo articolo è stato inserito nell'approfondimento "Effetti e principi della Meccanica Quantistica", del quale si consiglia la lettura.
QUI e QUI trovate una trattazione molto semplice (e divertente) dell'effetto Compton, particolarmente adatta a ragazzi e neofiti di tutte le età.
Continuiamo a giocare a biliardo (in modo più realistico), preparando il terreno a delle palle molto particolari e a effetti quantistici come quello fotoelettrico e quello Compton. Chissà quanti giocatori di biliardo, vedendo schizzare le due sfere in direzioni diverse, pensano che la stessa cosa stia capitando nel microcosmo delle particelle? Fatemi sperare che qualcuno lo faccia… Se no, pazienza: lo faremo noi!
QUI la prima parte dell'articolo dedicato all'effetto Compton
Mettiamo le mani avanti sui vettori
Una prefazione a questo articolo. Come vedrete esso non è certamente facile e ho pensato parecchio se scriverlo in questo modo o limitarmi alla parte quantistica. Oltretutto non sarebbe nemmeno stato difficile renderla abbastanza semplice e intuitiva. Tuttavia, le leggi di conservazione dell’energia e della quantità di moto sono troppo importanti nello stabilire un contatto diretto e apparentemente logico tra il mondo fisico che ci circonda e quello un po’ pazzo e assurdo della MQ. In altre parole, anche Alice usa -spesso- un linguaggio che riusciamo a comprendere. Un’occasione ghiotta che sicuramente non potevate perdervi.
Il problema è che il gioco del biliardo giocato su una sola dimensione (come fatto precedentemente) riesce a essere descritto abbastanza bene con espressioni matematiche di “basso” livello (somme e moltiplicazioni e poco altro). La situazione si complica abbastanza quando l’urto non è centrale e il moto delle due palle dopo l’urto segue direzioni diverse. Siamo nel caso della descrizione a due dimensioni. Essa è sicuramente la più interessante per i giocatori del tavolo verde, ma anche per le particelle del microcosmo. Potevo far trenta e non fare trentuno? Ho deciso quindi di affrontarla, anche se non si riesce ad arrivare alla soluzione del problema in quanto sarebbe necessario introdurre un parametro supplementare che complicherebbe davvero troppo le formule.
Tuttavia, l’importante per il mondo di Alice non è tanto arrivare a una soluzione, quanto impostare nel modo corretto le equazioni che derivano dalle due leggi di conservazione. E a questo punto “dovevo” arrivare.
Qual è la vera difficoltà della trattazione che ho deciso di proporvi? Presto detto: l’introduzione dei vettori e della loro scomposizione nelle due componenti lungo gli assi x e y. Questo comporta un po’ di geometria e una buona dose di trigonometria spicciola. Qualcosa in più di quanto fatto nella serie dedicata alla matematica. Nel libro “La Fisica addormentata nel Bosco” è spiegato ampiamente cosa sono i vettori e come ci si deve comportare per calcolarne le componenti e determinare il vettore somma e differenza. Non posso ripetere qui tutti i concetti relativi, ma almeno accennare alla problematica e permettervi di utilizzarla con un minimo di fatica mentale.
Il vero punto chiave da capire è che energia cinetica e quantità di moto sono grandezze decisamente differenti da un punto di vista fisico. La prima è un numero, uno “scalare”, che si calcola conoscendo solo il valore del modulo della velocità (oltre alla massa, ovviamente), dove per modulo si intende il valore numerico associato a un vettore (fatemi dire la sua intensità). La quantità di moto è invece un vettore vero e proprio, dato che tale è la velocità. Esso è quindi identificato non solo dal suo modulo, ma anche da una direzione e da un verso. In altre parole, una certa velocità di modulo v, può essere disegnata comunque nel piano del foglio, girandola e spostandola come si vuole. Il suo valore numerico rimane sempre lo stesso, ma il vettore cambia continuamente. Vediamo quanto detto nella Fig. 3. I vettori v, v1 e v2 sono diversi, pur avendo lo stesso modulo v.
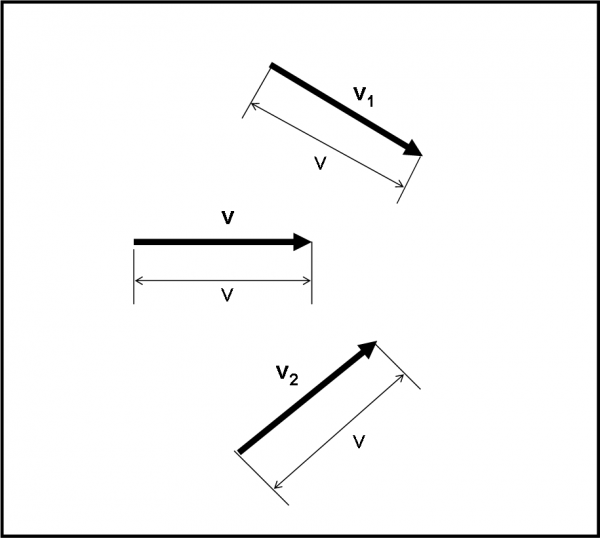
Perché nell’articolo precedente non avevo fatto distinzione tra vettore e modulo? Presto detto: l’urto avveniva lungo una sola direzione e nella stessa direzione potevano muoversi le due sfere. Sommare o sottrarre due vettori che stanno sulla stessa retta porta automaticamente alla somma o alla differenza dei moduli dei vettori. Era, quindi, del tutto inutile introdurre un concetto supplementare. Andando, adesso, nel piano della figura, non posso più tralasciare il concetto di velocità intesa come vettore. Per distinguere subito i vettori dai numeri, i primi saranno i soli a essere scritti in grassetto.
Sommiamo i vettori e calcoliamo le componenti
Affrontiamo, quindi, il problema della somma di due vettori e di come si utilizzano le loro componenti per avere espressioni composte da numeri. A seguito di un urto non frontale (ossia tale che la direzione della prima palla non passi per il centro della seconda) le due sfere seguono percorsi diversi. Facciamo subito una semplificazione, che -comunque- tale non è dato che si può sempre cambiare il sistema di riferimento in cui si descrive l’urto. Immaginiamo che la seconda sfera sia immobile e che si muova solo la prima. Dopo un urto non frontale (e ci torneremo sopra tra poco) le due sfere si muovono entrambe seguendo percorsi diversi. In altre parole, un vettore velocità (e quantità di moto), diretto lungo un asse, si divide in due vettori che formano un certo angolo fra di loro. La conservazione della quantità di moto assume, allora, una forma ben più generale, ossia:
m1v1 + m2v2 = m1v1’ + m2v2’
che, con l’ipotesi della seconda sfera immobile (v2 = 0), diventa:
m1v1 = m1v1’ + m2v2’
Notate i termini in grassetto, che indicano chiaramente che stiamo lavorando con vettori su un piano. La relazione precedente ci dice che un vettore diretto lungo una certa direzione (prima dell’urto) è uguale alla somma di due vettori diretti in direzioni diverse tra di loro e diverse dalla direzione della prima palla. L’uguaglianza è permessa dalla conservazione della quantità di moto. In realtà, i vettori velocità sono moltiplicati per un numero (la massa), ma questo non cambia la situazione, dato che un vettore moltiplicato per uno scalare rimane un vettore che ha la stessa direzione di quello precedente e anche lo stesso verso (la massa è sempre positiva). Ciò che cambia è solo il modulo, ossia la parte numerica, che non pone alcun problema.
La relazione (1), può essere sintetizzata da:
r = r1 + r2
Potremmo dire che vale anche r = r1 + r2, come fatto la volta scorsa lavorando su una sola dimensione? Ossia, potremmo passare da una somma di due vettori alla somma dei loro moduli? Assolutamente NO. Il vettore somma di due vettori NON ha come modulo la somma dei moduli dei due vettori. Questo capita solo se i vettori giacciono tutti su una stessa retta. Ora non più. Dobbiamo, perciò, imparare a sommare due vettori e a determinare il modulo del vettore somma. Solo così potremo scrivere una relazione vettoriale attraverso qualcosa di numerico che esprima la conservazione della quantità di moto in maniera “calcolabile”.
Limitiamoci qui a ricordare soltanto la regola del parallelogramma, ossia il metodo rapido, geometrico e veloce per determinare la somma di due vettori e il valore del modulo del vettore somma. Lo vediamo in Fig. 4.
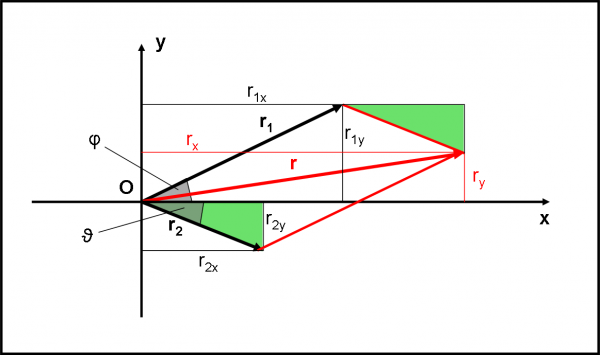
La somma dei vettori r1 e r2 si ottiene costruendo il parallelogrammo rosso. Il vettore rosso è proprio il vettore somma. Il suo modulo si ottiene considerando le componenti r1x, r1y e r2x, r2y dei due moduli r1 e r2 . Risulta:
rx = r1x + r2x
ry = r1y + r2y …. (2)
e, infine:
r = (rx2 + ry2)1/2
il modulo del vettore somma è dato, quindi, dalla radice quadrata dei quadrati delle sue componenti x e y, che si ricavano dai moduli dei due vettori iniziali attraverso la (2). Ribadisco ancora che non vale, quindi, la semplice relazione r = r1 + r2, che ha senso soltanto quando i due vettori giacciono sulla stessa retta.
La (2) si ricava facilmente considerando l’uguaglianza dei triangoli verdi. Rifletteteci sopra e riuscirete a dimostrarlo da soli.
La relazione (2) si esprime molto meglio attraverso le funzioni trigonometriche seno e coseno. In particolare, si ha che:
r1x = r1 cos φ
r1y = r1 sen φ
r2x = r2 cos ϑ
r2y = - r2 sen ϑ
Da cui segue:
rx = r1 cos φ + r2 cos ϑ
ry = r1 sen φ - r2 sen ϑ …. (2)
Sì, lo ammetto, questa parte è sicuramente un po’ impegnativa (ma potete riuscire a seguirla, ne sono sicuro). Tuttavia, spiegarla meglio vorrebbe dire allargare il discorso in modo notevole. Sono sicuro che, andando a rileggere con attenzione la definizione delle funzioni trigonometriche, le formule precedenti risulteranno più che comprensibili. Al limite, vedremo di aggiungere un’appendice…
La conservazione della quantità di moto si fa in due
Adesso, però, torniamo alle nostre palle di biliardo. Cosa c’entra con loro tutto il discorso fatto sulla somma e sulle componenti dei vettori? Moltissimo. La conservazione della quantità di moto espressa da una relazione vettoriale (m1v1 = m1v1’ + m2v2’) può essere scomposta in due relazioni scalari (numeriche) relative alle due componenti dei moduli dei vettori secondo l’asse x e l’asse y, utilizzando le relazioni scritte per r1 e r2.
Una relazione vettoriale porta a due relazioni scalari, che si ottengono separando la componente x da quella y.
Non più due equazioni (le leggi di conservazione), ma tre equazioni: due provenienti dalla conservazione della quantità di moto e una da quella dell’energia cinetica. Purtroppo, però, non bastano per risolvere completamente il problema. Infatti le incognite sono quattro (le componenti delle velocità delle due sfere dopo l’urto v1x’, v2x’, v1y’ e v2y’), mentre le equazioni che le legano sono solo tre. Niente da fare, è necessario sapere qualcosa di più… Tuttavia, noi non siamo veramente interessati a risolvere il problema (non dobbiamo vincere un trofeo di biliardo), ma solo a scrivere le equazioni che stabiliscono il problema.
Scriviamo allora le tre equazioni derivanti dalle leggi di conservazione e ragioniamoci sopra.
Nessun problema per l’energia cinetica
½m1v12 + ½ m2v22 = ½ m1v1’2 + ½m2v2’2
Questa relazione non cambia passando da una rappresentazione a una dimensione a una rappresentazione a due, dato che le velocità compaiono solo con il loro modulo e non ci importa quali siano le loro direzioni e il loro verso.
Per quanto detto all’inizio possiamo eliminare il secondo termine di sinistra, dato che abbiamo assunto la seconda palla ferma (v2 = 0). La relazione diventa
½ m1v12 = ½ m1v1’2 + ½ m2v2’2
La conservazione della quantità di moto è invece data da:
m1v1 + m2v2 = m1v1’ + m2v2’
La relazione vettoriale si trasforma nelle due espressioni numeriche (ossia scalari) delle sue componenti:
m1v1x + m2v2x = m1v1x’ + m2v2x’
m1v1y + m2v2y = m1v1y’ + m2v2y’ …. (3)
Possiamo fare qualche semplificazione. Innanzitutto la velocità v2 è uguale a zero e quindi lo sono anche le sue componenti (v2x = v2y = 0). Inoltre la velocità v1 è diretta proprio lungo l’asse x e quindi la sua componente secondo y è anch’essa uguale a zero (v1y = 0, v1 = v1x).
Le (3) diventano:
m1v1 + 0 = m1v1x’ + m2v2x’
0 + 0 = m1v1y’ + m2v2y’
Le due leggi di conservazione ci danno quindi le tre equazioni (scalari):
½ m1v12 = ½ m1v1’2 + ½ m2v2’2
m1v1 = m1v1x’ + m2v2x’
0 = m1v1y’ + m2v2y’ …. (4)
Non illudiamoci di aver semplificato abbastanza per poter risolvere il problema. Le incognite sono sempre quattro e le equazioni tre. Ormai ci siamo e facciamo l’ultimo passo, di tipo trigonometrico. Le componenti delle due velocità finali possono essere scritte in funzione del modulo delle due velocità post-urto e dell’angolo che esse sottendono rispetto all’asse x (φ e ϑ) attraverso le (2).
Le (4) diventano:
m1v12 = m1v1’2 + m2v2’2
m1v1 = m1v1’cos φ + m2v2’cos ϑ (componente x)
0 = m1v1’sen φ – m2v2’sen ϑ (componente y) …. (5)
Non illudiamoci di avere come incognite soltanto i moduli delle velocità dopo l’urto (v1’ e v2’) e di poter risolvere il problema. Compaiono, infatti, due angoli che sono entrambi sconosciuti.
Su, non arrabbiatevi. L’uso delle funzioni trigonometriche è più che normale nelle equazioni e porta a grandi semplificazioni pratiche e concettuali. Dobbiamo entrare in quest’ottica prima o poi. Basta rifletterci un po’ sopra e i passaggi fatti appariranno veramente banali: basta ricordarsi la definizione di seno e coseno e poco di più…
Le equazioni (5) sono quelle che ci servono per cambiare il tavolo da gioco. Tuttavia, usiamole ancora un attimo per illustrare un caso particolare che è poi quello normale nel gioco del biliardo. In esso le due sfere sono uguali e hanno la stessa massa, ossia m1 = m2 = m. Proviamo a scrivere le nuove relazioni. Anzi, possiamo scriverle per quello che sono, senza passare alle componenti e alle funzioni trigonometriche. Sono o non sono un “buono”?
mv1 = mv1’ + mv2’ (somma vettoriale che vale due relazioni scalari)
mv12 = mv1’2 + mv2’2 (ho eliminato il fattore ½ comune a tutti i fattori)
Beh… “m” è sempre la stessa e si può eliminare tranquillamente:
v1 = v1’ + v2’
v12 = v1’2 + v2’2
Queste due relazioni hanno un significato ben più profondo di quanto possa sembrare a prima vista. La prima ci dice che il vettore v1 è proprio la somma dei vettori v1’ e v2’. In altre parole, ci dice che vale la regola del parallelogramma che abbiamo visto nella Fig. 4. La seconda è ancora più importante, anche se lavora solo sui moduli. La riconoscete? Sicuramente sì. Non è altro che il teorema di Pitagora! Non solo i due vettori v1’ e v2’ danno coma somma il vettore v1, ma i loro moduli soddisfano il teorema di Pitagora, ossia il triangolo OAB è rettangolo (Fig. 5)! Notate che i vettori sono stati scritti in grassetto, mentre i loro moduli no.
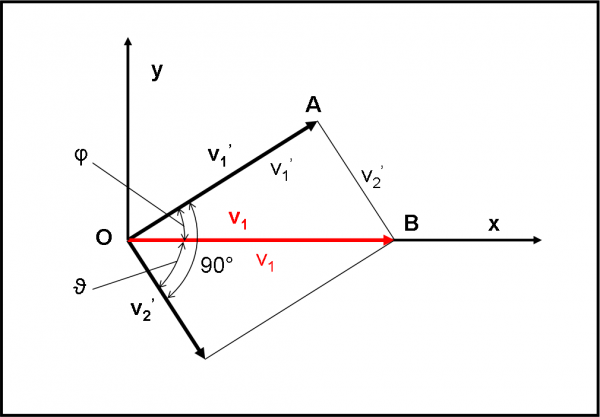
Questo vuole anche dire che la somma di φ e di ϑ vale 90° gradi. Esprimiamo queste considerazioni attraverso poche parole e la Fig. 6. Quando le due sfere si toccano, la seconda si muove lungo la direzione indicata dalla congiungente i centri delle due sfere. La prima è, invece, costretta a muoversi lungo una linea perpendicolare a quella precedente. Ribadiamo, ancora, che questa situazione è valida solo se le masse sono uguali. In caso contrario il triangolo non è più rettangolo e la somma degli angoli non è più 90°. Beh, se non altro abbiamo imparato a colpire la palla ferma e a intuire dove andranno entrambe… Se falliamo come fisici quantistici ci daremo al … biliardo!
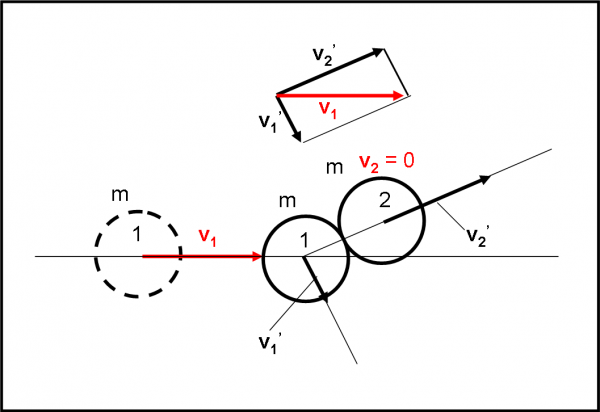
Un biliardo microscopico
Nel tavolo da gioco delle particelle le masse sono qualcosa di ben diverso e non ha nemmeno senso parlare di massa “costante” quando si è nel regime della velocità della luce. Le masse diventano relativistiche e il loro significato ben più complesso, soprattutto per il fotone. Siamo finalmente pronti a fare il viaggio attraverso un microscopio dinamico eccezionale che ci porti nel mondo della meccanica quantistica. Vediamo, un po’ alla volta, come l'urto tra le palle da biliardo descritto dalla (5) si trasformino in qualcosa di ben diverso. Tuttavia, il concetto di base è simile e valgono sempre le stesse leggi di conservazione. Questo è il punto chiave di tutto il discorso fatto fin qui.
Parliamo dell’effetto Compton, ma poi vedremo come esso rientra in un discorso ben più generale che contiene sia l’effetto fotoelettrico che la dispersione della luce nell’atmosfera terrestre che ci fa vedere il cielo blu. Capiremo che, in fondo, è solo una questione di energia che si dà alla palla che comanda il gioco sul tavolo verde.
Diamo risalto a un concetto fondamentale: “Perché questi urti tra particelle acquistano un’importanza così grande nella storia della meccanica quantistica?” Facile rispondere. I giocatori, o meglio le sfere in gioco, sono il fotone e l’elettrone. Se il secondo potevamo anche immaginarcelo come corpo solido e concreto, lo stesso non era certo ovvio per il fotone. La luce era pensata come onda. Il fatto che si comportasse come una particella solida dotata di una certa quantità di moto e di energia implicava una visione a dir poco rivoluzionaria. In altra parole, un’ulteriore prova del comportamento ambiguo delle particelle, a volte onde e a volte corpuscoli come perfettamente evidenziato dall’esperimento delle due fenditure di Feynman, che ormai conosciamo molto bene. Se l’effetto fotoelettrico sembra più vicino a uno sparo che faccia schizzare un frammento da una superficie solida, l’effetto Compton assomiglia molto di più a un colpo del gioco del biliardo: entrambe le sfere proseguono il loro cammino seguendo le regole definite precedentemente nel caso dell’urto a due dimensioni. Facciamoci aiutare dalla Fig. 7 per una visione qualitativa e dalla Fig. 8 per una descrizione più accurata.
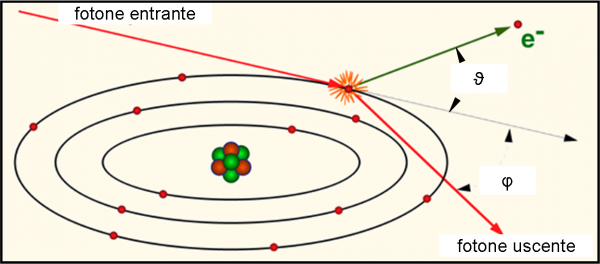
Un’onda luminosa colpisce un atomo e, in particolare, uno dei suoi elettroni più esterni. L’onda, a questo punto, non va più considerata come tale, ma come una piccola sfera dotata di massa e velocità. Essa trasferisce parte della sua energia cinetica all’elettrone, riesce a staccarlo dall’atomo e a smuoverlo dalla sulla sua orbita. Esso diventa libero (e l’atomo si ionizza) e si muove in una certa direzione (come sappiamo bene dalla trattazione di meccanica classica precedente). Anche il fotone, però, continua la sua corsa (diversamente dall’effetto fotoelettrico) anche se con un energia diversa (la velocità è però sempre la stessa, quella della luce). Ciò che cambia in lui è la lunghezza d’onda e la direzione dello spostamento. Perdita di energia vuol dire allungamento della lunghezza d’onda (arrossamento) e spostamento rispetto alla direzione originale vuol dire dispersione o scattering.
Ecco perché l’effetto viene anche chiamato scattering Compton. Cosa si vede in realtà? Si nota un cambiamento della lunghezza d’onda della luce che può essere spiegata solo e soltanto attraverso un urto tra particelle. Uno dei capisaldi della meccanica quantistica! La Fig. 7 ci descrive qualitativamente lo scattering Compton, che dà luogo a uno spostamento dell’elettrone e a un indebolimento energetico del fotone, rivelabile attraverso l’allungamento della lunghezza d’onda.
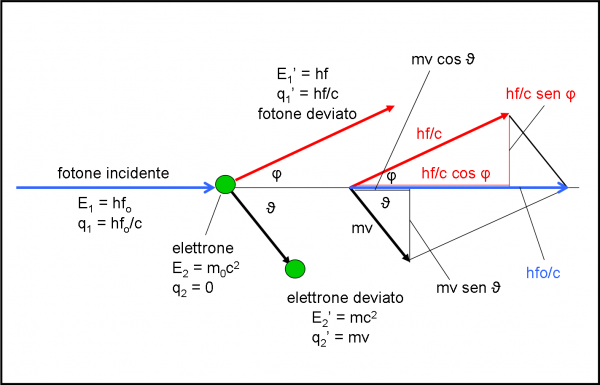
Ci può bastare la Fig. 7, dopo tutte le formule che abbiamo scritto per gli urti? Direi proprio di no e tentiamo allora di riscrivere le stesse formule nel caso dell’effetto Compton, utilizzando la più quantitativa Fig. 8, dove nella parte destra c’è proprio lo schema geometrico che descrive i vettori e le loro componenti. Il fotone prima dell’urto dà luogo a un “vettore” blu, mentre dopo l’urto a uno rosso. Ho scelto questi colori per evidenziare l’allungamento della lunghezza d’onda. C’ho pensato a lungo, ma penso proprio che siate in grado di seguire tutto il ragionamento. Un bel colpo, in quanto riusciamo a descrivere un fenomeno quantistico attraverso le leggi di un biliardo. Niente male!
Riscriviamo, allora, le equazioni (5):
m1v12 = m1v1’2 + m2v2’2
m1v1 = m1v1’cos φ + m2v2’cos ϑ (componente x)
0 = m1v1’sen φ – m2v2’sen ϑ (componente y) …. (6)
Dobbiamo eseguire qualche sostituzione. La velocità del fotone è conosciuta, ma non la sua massa. Anzi, esiste oppure no? Non nel senso che noi diamo normalmente a questa grandezza fisica, ma in termini quantistici sicuramente sì, come ci ha dimostrato Red nei suoi articoli sulla MQ.
Beh, innanzitutto devo inserire nuovamente l’energia della seconda palla, dato che il fatto di stare ferma non annulla la sua energia. Un elettrone ha una sua energia anche da fermo…
Quanto vale? Beh… ce lo dice Einstein: E = moc2, dove mo è la massa a riposo dell’elettrone. Ricordiamo anche che se esso si muove la sua massa relativistica cambia secondo la legge;
m = mo/(1- v2/c2)1/2
Una vecchia formula che già conosciamo bene fin da quando abbiamo parlato di dilatazione del tempo e di accorciamento delle distanze. Non posso andare oltre, se no sarei costretto a scrivere la teoria della relatività, almeno quella ristretta. Prendiamola per buona e se non ci credete prendetevela con Albert.
Qual è l’energia del fotone in termini quantistici? Essa è data dalla frequenza moltiplicata per la costante di Planck, ossia:
E = hfo
Come vedete non compare esattamente la massa, che non esiste, ma l’importante è che si possa scrivere l’energia del fotone. In questo modo possiamo tranquillamente conservare l’energia totale.
La prima equazione della (6) diventa:
hfo + moc2 = hf + mc2 (m è dato dalla formula precedente)
Dove f è la frequenza dopo l’urto. Passiamo, adesso alle due equazioni relative alla conservazione della quantità di moto.
L’energia del fotone è hfo. Se vogliamo la sua quantità di moto basta dividerla per la velocità, ossia c. Abbiamo quindi che la quantità di moto del fotone non è altro che hfo/c (banale!). Quello dell’elettrone è invece dato dal solito prodotto mv, dove però m è la massa relativistica. L’elettrone è proprio una piccola palla di biliardo. Le due equazioni diventano:
hfo/c = hf/c cos φ + mv cos ϑ
0 = hf/c sen φ – mv sen ϑ
Mettendo tutto insieme abbiamo:
hfo + moc2 = hf + mc2
hfo/c = hf/c cos φ + mv cos ϑ
0 = hf/c sen φ – mv sen ϑ
In fondo è cambiato ben poco, come concetto, anche se le grandezze che compaiono sono “leggermente” diverse.
Cosa si osserva in pratica? Non certo lo spostamento delle sferette o cose analoghe al biliardo. Ciò che si osserva è il cambiamento della lunghezza d’onda del fotone (ossia della luce che urta un atomo). Nelle equazioni, la lunghezza d’onda compare attraverso il suo inverso, la frequenza f. Vi evito una serie un po’ noiosa di passaggi matematici (chi vuole provarci può tentare, ma non mi chieda poi di raccontarlo a tutti… mi sembrerebbe eccessivo… almeno per adesso!) e scrivo subito il risultato:
Δλ = λ – λo = λc (1- cos φ)
Dove la quantità:
λc = h/moc
prende il nome di lunghezza d’onda di Compton ed è una costante che vale circa 2,4 · 10-12 m.
Essa permette di calcolare l’arrossamento della luce, ossia la differenza tra lunghezza d’onda dopo l’urto (λ) e quella iniziale (λo).
Ribadisco, che questo risultato osservativo può essere spiegato solo e soltanto attraverso una natura corpuscolare del fotone, ossia attraverso una sua interpretazione quantistica.
Vorrei concludere con un riassunto piuttosto semplificato, ma che può darvi un’idea della differenza tra vari fenomeni di scattering. Consideriamone tre, i più conosciuti.
Questione di energia
Il gioco è sempre lo stesso, con due palle da biliardo formate da un fotone e da un elettrone. Ciò che veramente cambia è l’energia che si trasmette nell’urto.
Il primo scattering è quello di Rayleigh. Esso è quello che comanda la visione azzurra del cielo. Ne avevamo già parlato QUI, ma possiamo ridefinirlo molto semplicemente. I fotoni che colpiscono gli atomi atmosferici vengono deviati, ossia diffusi, e questo capita soprattutto per le lunghezze d’onda più corte come quella del blu. L’energia in gioco è bassa e l’elettrone non è minimamente scalfito dall’urto. E’ il fotone che ne risente, ma solo per il cambiamento della sua direzione. Non perde alcuna energia. Questo effetto è servito ben poco alla meccanica quantistica, dato che la spiegazione può essere data tranquillamente attraverso la natura ondulatoria della luce. I fotoni potevano anche non esistere come particelle.
Se l’energia cresce il fotone scarica tutta la sua violenza sull’elettrone e riesce a staccarlo dalla sua posizione ancorata al nucleo atomico. Del fotone non si ha più memoria (ha dato tutto quello che aveva), ma nasce un elettrone libero che ci mostra l’effetto fotoelettrico. Esso si ottiene per valori di energia del fotone di poco superiori all’energia di legame dell’elettrone con il nucleo.
Per energie ancora superiori il fotone non solo riesce a staccare e a spostare l’elettrone, ma continua la sua corsa anche se molto più stanco e arrossato, allungando la sua lunghezza d’onda. Questo è, ovviamente, l’effetto Compton. L’energia del fotone è molto più grande dell’energia di legame e l’elettrone può essere considerato “libero” fin da subito.
Esiste anche un quarto effetto (di coppia) che nasce per energie ancora superiori, dove l’urto scompagina lo stesso nucleo atomico scagliando all’esterno un elettrone e un positrone, ma non esageriamo…
La faccenda non è veramente così semplice, dato che conta anche il tipo di atomo coinvolto e molte altre cose. Prendetela come una spiegazione molto qualitativa che serve, tuttavia, a farsi un’idea molto generale e intuitiva.
L’effetto Compton è valso anch’esso il Nobel nel 1922.
Beh… se siete riusciti a seguire tutto, senza spaventarvi, siete proprio bravi!
L’effetto inverso
Vale la pena accennare all’effetto Compton inverso. Esso è estremamente importante in quanto si nota benissimo nel rumore cosmico di fondo. Esso avviene quando l’energia del fotone è molto più piccola di quella dell’elettrone. In questo caso è possibile produrre fotoni ad altissima energia. Un esempio è proprio l’interazione tra un raggio cosmico (elettroni a grandissima energia) che si scontra contro i fotoni della radiazione cosmica di fondo. Questo effetto è decisamente impossibile da ottenere in un tavolo da biliardo, dato che implicherebbe che la nostra palla venga accelerata dall’urto contro una palla apparentemente immobile. Tuttavia, lasciamo alla MQ qualche freccia in più nel suo arco.





15 commenti
Ciao Enzo, sull'effetto Compton è l'ultimo articolo? Te lo chiedo così mi leggo di fila i 2 articoli.
Nel caso ve ne fossero altri allora preferirei aspettare, perché tra un pezzo e l'altro potrei scordarmi tutto
vai tranquillo... è l'ultimo
Caro Enzo, , all'apparenza banale: perché l'elettrone prima dell'urto viene considerato "fermo" (q2 = 0)? Fermo rispetto a che cosa?
, all'apparenza banale: perché l'elettrone prima dell'urto viene considerato "fermo" (q2 = 0)? Fermo rispetto a che cosa?
Perdona la domanda
fermo va inteso come "legato" all'atomo di cui fa parte e non libero di muoversi ionizzandolo. In questo senso non ha quantità di moto.
Grazie Enzo, Probabilmente, il paragone con il biliardo mi ha tratto un po' in inganno, facendomi pensare a "fermo" nel senso di "immobile", come la palla sul tavolo verde, cosa che, naturalmente, per un elettrone non ha molto senso.
Probabilmente, il paragone con il biliardo mi ha tratto un po' in inganno, facendomi pensare a "fermo" nel senso di "immobile", come la palla sul tavolo verde, cosa che, naturalmente, per un elettrone non ha molto senso. 

In effetti avevo cominciato a pensarci dopo che ti avevo inviato il commento.
A questo punto, con questa storia della quantità di moto nulla, mi avete fatto venire un'altra domanda: le caratteristiche dell'Effetto Compton possono dipendere dalla temperatura (intendo, dell'atomo/elettrone che viene urtato)? La formuletta della lunghezza d'onda di Compton sembrerebbe dire di no ma mi viene da pensare che comunque un elettrone "caldo" o uno "freddo" reagiscano in maniera diversa all'urto del fotone incidente. Mi chiedo, cioè, se sia solo una questione di maggiore o minore probabilità che lo scattering avvenga o se la temperatura incida anche sulle caratteristiche dello stesso.
L'ho buttata lì, sia chiaro, solo per estendere la discussione...
caro Pier,
sembra che la temperatura o se vuoi l'eccitazione dell'atomo conti ben poco. Ciò che domina è l'energia del fotone, tale da poter considerare l'elettrone completamente libero e slegato rispetto al nucleo.
Ciao Enzo, la prima espressione dovrebbe essere:
m1v1 + m2v2 = m1v1’ + m2v2’
anziché:
m1v1 + m2v2 = m1v1’ + m1v2’
e la seconda diventa:
m1v1 = m1v1’ + m2v2’
ah... se non ci fossi tu... Forse non ero ancora pronto a scrivere questa seconda parte... Se trovi altro dimmelo... ho gli occhi foderati...
questa seconda parte... Se trovi altro dimmelo... ho gli occhi foderati... 
Ciao Enzo, com'è possibile individuare nella CMB i fotoni che hanno subito l'effetto Compton e quelli che hanno subito il Compton inverso?
Inoltre alcuni astronomi "alternativi" hanno tentato di spiegare proprio la CMB con l'effetto Compton, in che modo possiamo categoricamente escludere questa ipotesi?
caro SMA,
la risposta potrebbe trovarsi quasi completamente qui:
http://www.infinitoteatrodelcosmo.it/2014/01/17/le-deformazioni-della-radiazione-di-fondo/
Per ottenere un Compton inverso è necessario che i fotoni della CMB attraversino una zona con elettroni molto energetici e si vedrebbero fotoni molto ringalluzziti. Il viceversa è più difficile, anche perché l'energia dei fotoni non sarebbe sufficiente a staccare elettroni.
Sull'origine del CMB potrei solo dire che certe anisotropie potrebbero anche essere dovute all'effetto Compton, ma non certo tutta la radiazione... ciò che si osserverebbe sarebbe sicuramente diverso come distribuzione e intensità e molte altre cose.. e , in generale, si vedrebbe ben poco (i poveri fotoni perderebbero molta energia e già ne perdono tanta per il lungo viaggio...).
.
Infatti pensavo che questo effetto non potesse spiegare una radiazione uniforme come la CMB, del tutto simile ad un corpo nero.
Eccomi!
Come al solito in super ritardo
Stavolta ammetto di aver fatto veramente fatica a comprendere fino in fondo tutto l'articolo (sempre ammesso che io l'abbia veramente compreso fino in fondo)... forse è anche la stanchezza del novo incarico di lavoro che sto svolgendo da qualche settimana... comunque sia non mi arrendo, pian piano recupererò di nuovo in terreno perso (cioè tutti articoli che hai pubblicato finora).
Niente altro... grazie come sempre!
Alex.
Caro Enzo, ho deciso di rileggere questo articolo alla luce di una recente discussione (quella su vedere l'invisibile).
Ho letto più volte questo articolo, più che altro perché mi sono intestardito sulle operazioni matematiche da eseguire per trovare la relazione:
Δλ = λ - λ0 = λc (1 – cosφ)
Proprio non c'era verso di trovare la soluzione.......
Dopo vari tentativi, però, penso di aver trovato la strada da seguire , per cui riporto per intero passaggi e ragionamento, che personalmente mi serve per come esercizio per irrobustire e verificare le mie poche conoscenze di matematica, dall'altro spero possa servire da spunto a chi magari come me si è posto il medesimo problema (anche per questo riporto tutti i passaggi).
, per cui riporto per intero passaggi e ragionamento, che personalmente mi serve per come esercizio per irrobustire e verificare le mie poche conoscenze di matematica, dall'altro spero possa servire da spunto a chi magari come me si è posto il medesimo problema (anche per questo riporto tutti i passaggi).
Innanzitutto, sono partito da quanto riporti nell'articolo (facilmente deducibile dalla figura 8).
L'energia del sistema prima e dopo l'urto si deve conservare, per cui:
E1 + E2 = E'1 + E'2
hf0 + m0c^2 = hf + mc^2
Anche la quantità di moto di deve conservare, quindi:
Q1 + Q2 = Q'1 + Q'2
hf0/c+ m0 V0 = hf/c + mV
Dato che l'elettrone prima dell'urto, rispetto al fotone, si considera fermo, V0 è uguale a zero, per cui:
hf0/c = hf/c + mV
Trattandosi di vettori:
hf0/c = hf/c cos φ + mV cos ϑ componente x
0 = hf0/c sen φ - mV sen ϑ componente y
Ci sono due angoli, meglio ridurlo a uno, usando le componenti del vettore mV.
mV cos ϑ = hf0/c - hf/c cos φ
mV sen ϑ = hf0/c sen φ
Grazie a Pitagora, la somma dei quadrati delle componenti x ed y del vettore mV, sono uguali al quadrato del modulo di tale vettore (ipotenusa di un triangolo), quindi:
(mv)^2 = (hf0/c - hf/c cos φ ) ^2 + (hf0/c sen φ) ^2
(mv)^2 = (hf0/c)^ 2 + (hf/c)^2 cos^2φ – 2 (hf0/c) (hf/c) cosφ + (hf0/c)^2 sen^2 φ
metto in evidenza (hf/c)^2 ricordando che sin^2(α) + cos^2(α) = 1
(mv)^2 = (hf0/c)^ 2 + (hf/c)^2 (cos^2φ + sen^2 φ ) – 2 (hf0/c) (hf/c) cosφ 2 φ
m^2 v^2 = (hf0/c)^ 2 + (hf/c)^2 – 2 (hf0/c) (hf/c) cosφ
La relazione che lega la massa a riposo dell'elettrone da quella a velocità V, è:
m = m0 /(1 – V^2/c^2) ^ 1/2
per eliminare la radice quadrata è possibile elevare entrambi al quadrato:
m^2 = m0^2 /(1 – V^2/c^2)
m^2 (1 – V^2/c^2) = m0^2
m^2 – m^2V^2/c^2 = m0^2
Dato che:
hf0 + m0c^2 = hf + mc^2
mc^2 = hf0 - hf + m0c^2
si potrebbero usare le due relazioni trovate, ma nella prima la massa compare al quadrato, per cui è possibile elevare al quadrato la seconda:
(mc^2)^2 = (hf0 - hf + m0c^2 )^2
m^2c^4= (hf0)^2 – h^2f0 f + hf0 m0c^2 - h^2f0 f + (hf)^2- hfm0c^2+ hf0 m0c^2 – hfm0c^2 + m0^2c^4
m^2c^4= (hf0)^2 + (hf)^– 2h^2f0 f + 2hf0 m0c^2- 2hfm0c^2 + m0^2c^4
Ora è possibile riprendere la prima relazione trovata:
m^2 – m^2V^2/c^2 = m0^2
moltiplicando entrambi per c^4
m^2c^4 – m^2V^2c^4/c^2 = m0^2c^4
m^2c^4 – m^2V^2c^2 = m0^2c^4
m^2c^4 = m0^2c^4+ m^2V^2c^2
Eguagliando le relazioni :
(hf0)^2 + (hf)^2 – 2h^2f0 f + 2hf0 m0c^2- 2hfm0c^2 + m0^2c^4 = m0^2c^4+ m^2V^2c^2
(hf0)^2 + (hf)^2 – 2h^2f0 f + 2hf0 m0c^2- 2hfm0c^2 = + m^2V^2c^2
Ma m^2V^2 è proprio il quadrato del modulo del vettore mV, che era stato calcolato all'inizio:
m^2 v^2 = (hf0/c)^ 2 + (hf/c)^2 – 2 (hf0/c) (hf/c) cosφ
m^2 v^2 = (hf0)^2/c^ 2 + (hf)^2/c^ 2 – 2 (hf0)/c^ 2 (hf)/c^ 2 cosφ
m^2 v^2 c^ 2 = (hf0)^2+ (hf)^2 – 2 h^2 f0 f cosφ
Per cui:
(hf0)^2 + (hf)^2 – 2h^2f0 f + 2hf0 m0c^2- 2hfm0c^2 = (hf0)^2+ (hf)^2 – 2 h^ 2f0 f cosφ
-2h^2f0 f + 2hf0 m0c^2- 2hfm0c^2 = – 2 h^ 2f0 f cosφ
Dividendo tutto per 2h f0 f
-2h^2f0 f /2h f0 f + 2hf0 m0c^2/2h f0 f - 2hfm0c^2/2h f0 f = – 2 h^ 2f0 f/2h f0 f cosφ
-h + m0c^2/f - m0c^2/ f0 = – h cosφ
m0c^2/f - m0c^2/f0 = – h cosφ + h
m0c^2 (1/f - 1/f0) = h – h cosφ
m0c^2 (1/f - 1/f0) = h (1 – cosφ)
(1/f - 1/f0 ) = h (1 – cosφ) / m0c^2
(1/f - 1/f0 ) = h/m0c^2 (1 – cosφ)
moltiplicando entrambi per c
(c/f - c/f0 ) = hc/m0c^2 (1 – cosφ)
(c/f - c/f0 ) = h/m0c (1 – cosφ)
La lunghezza d'onda luminosa è legata alla frequenza dalla seguente relazione:
λ = c/f
Quindi:
Δλ = λ - λ0 = h/m0c (1 – cosφ)
Ovviamente si può anche calcolare la differenza di frequenza
(1/f - 1/f0 ) = h/m0c^2 (1 – cosφ)
1/(f - f0 ) = 1/m0c^2 h (1 – cosφ)
m0c^2 /(f - f0 ) = h (1 – cosφ)
m0c^2 = h (1 – cosφ) (f - f0 )
m0c^2 /h (1 – cosφ) = f - f0
Δf = f - f0 = m0c^2 /h (1 – cosφ)
In ultimo devo ancora riflettere bene sull'effetto inverso a quello Compton (elettroni altamente energetici e fotoni un po' fiacchi).
Paolo
Paolo... e meno male che hai poche conoscenze di matematica...
Che dire, sono proprio in buone mani! :-P. Sull'inverso non ci sono problemi... te lo assicuro!
Temo di avere "creato" dei mostri!!!!!!
Gulp così mi fai arrossire
In realtà ho solo applicato la matematica che tu hai descritto (e mi mancano ancora parecchi articoli da leggere) e un po' di logica (e poi conoscevo già il risultato da ottenere ).
).
A mio avviso, provare a sviluppare i concetti esposti nei suoi articoli, permette di approfondire e verificare se e cosa si è afferrato e quali sono le lacune rimaste.
A volte ragionandoci sopra tali lacune si colmano e si prende maggior confidenza con gli argomenti trattati.
Personalmente spero che esporre i propri ragionamenti, ma anche i dubbi, possa servire da stimolo anche ad altri per approfondire gli argomenti.
Più di una volta mi è capitato di comprendere meglio quanto descritto nei suoi articoli leggendo i commenti, i dubbi, le riflessioni...
Per esempio, in questo caso sono partito dalle tre equazioni iniziali (conservazione Energia, quantità di moto e rapporto tra massa in movimento e massa a riposo dell'elettrone), per trovare il valore della variazione di frequenza.
h; c; m0 e f0 erano valori noti, per cui il problema era trovare il valore della massa e della velocità dell'elettrone dopo l'urto.
La massa compariva sia legata alla velocità (mv) sia alla velocità della luce (mc).
Dopo due giorni di riflessione e tentativi vari (fogli su fogli di equazioni che non portavano a nulla, condite da qualche errorino ), ho semplicemente cercato di vedere come trovare mV e mC, confrontando le diverse soluzioni che offrivano le tre equazioni iniziali.
), ho semplicemente cercato di vedere come trovare mV e mC, confrontando le diverse soluzioni che offrivano le tre equazioni iniziali.
Paolo