Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Nelle puntate precedenti abbiamo descritto le condizioni in cui dal Sole si può vedere il transito dei satelliti medicei sul disco di Giove. Sono bastati un pizzico di trigonometria -e tanti disegni- per stabilire una regola base, applicabile a tutti i sistemi satellitari del Sistema Solare e non solo. Siamo anche riusciti a rappresentare la situazione sulla sfera celesta giovicentrica e a descrivere istante per istante la posizione dell’osservatore Sole in modo da determinare immediatamente se un evento può o non può capitare. Facendo diventare il Sole la stella che è, abbiamo, inoltre, usato i risultati ottenuti per descrivere le eclissi mutue tra satelliti e Giove, dato che la situazione è perfettamente speculare. Abbiamo, infine, concluso che quando capita un’eclisse, essa può essere vista da una platea estremamente estesa.

Finora si sono considerati i satelliti e il disco di Giove. Abbiamo, sicuramente, giocato facile, dato che i satelliti sono molto vicini a Giove e il disco del pianeta è molto grande. La conclusione è stata che le condizioni di visibilità dei transiti visti dal Sole sono quasi sempre rispettate e, di conseguenza, anche delle eclissi di Sole viste da Giove. Non vi è nemmeno bisogno di fare girare il Sole come un Super Kepler: qualsiasi posizione è utile.

Restringiamo Giove e il concetto non cambia…

E’venuto il momento di complicarci le cose e di fare un passo in più. Normalmente, si cerca di rivestire questo passaggio come un qualcosa di molto più complesso, che solo gli esperti possono risolvere. E, invece, non è vero. La configurazione e il procedimento rimangono gli stessi. Di cosa sto parlando? Beh… dei transiti, visti dal Sole, di un satellite davanti a un altro o, specularmente, di un eclissi di Sole vista da un satellite per colpa di un fratellino.

Cosa cambia realmente rispetto a prima? Pochissimo: invece del disco di Giove, dobbiamo considerare il disco del satellite che subisce il transito o l’eclisse, e, invece della distanza satellite-Giove, la distanza tra i due satelliti. La formuletta ce l’abbiamo già e basta inserire i parametri al suo interno per stabilire le condizioni di visibilità tra satellite e satellite. In altre parole, basta escludere Giove dal gioco. Lui continua a essere presente solo perché i satelliti sono vincolati a girare sul suo piano equatoriale e quindi a rivolvere attorno al Sole. Ne segue, quindi, che l’equatore gioviano rimane il piano di riferimento, tale e quale a prima.

Meglio di tante parole, conviene inserire una banalissima figura che spieghi la situazione. Usiamo la Fig. 20. Nella parte bassa vi sono i soliti due satelliti (1) e (2); il piano equatoriale di Giove, dove stanno i satelliti; la direzione del Sole, la cui declinazione è al massimo l’inclinazione orbitale i; la linea azzurra che è quella che caratterizza l’angolo limite del satellite (1), ossia la declinazione necessaria per essere visto transitare davanti a Giove. Insomma, proprio quello che abbiamo fatto finora e che ci ha portato a tutte le figure dei capitoli precedenti.

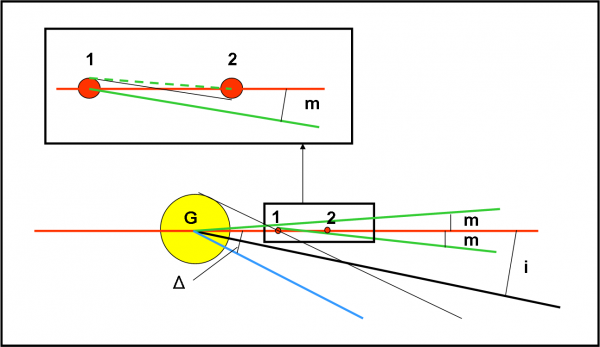
Cosa vogliamo aggiungere, adesso? Le condizioni di visibilità limite affinché il satellite (2) transiti davanti a (1) se visto dal Sole. Come vi dicevo cambia solo il diametro e la distanza… Possiamo già aspettarci il risultato. E’ vero che i satelliti sono più vicini tra loro di quanto non lo siano a Giove (almeno a due a due), ma il loro diametro è ridicolo rispetto a quello del pianeta. Ne consegue che l’angolo limite di visibilità m sarà sicuramente più piccolo di quello trattato finora. E, come conseguenza, sarà più difficile per il nostro Sole (o Super Kepler) riuscire ad assistere all’evento. Abbiamo comunque una sicurezza. Sia come sia quest’angolo limite, vi saranno sempre due punti in cui la visione sarà possibile! Ormai lo sappiamo bene: sono i due nodi tra equatore e orbita di Giove (o del Sole, come preferite). Non abbiamo perciò molta ansia a proseguire, sapendo che ci saranno sempre due configurazioni utili. E’ bello possedere un Super Kepler “naturale” come il Sole: e’ sempre una garanzia di successo.

Torniamo alla Fig. 20 e ingrandiamo nel riquadro la parte che ci interessa, ossia quella che identifica l’angolo m, il nuovo angolo di visibilità limite tra (1) e (2). Ripeto ancora che esso identifica l’angolo limite per assistere dal Sole a un transito di (2) davanti a (1). In altre parole, la declinazione del Sole deve essere inferiore a m per godersi lo spettacolo. E’ così difficile ricavare l’angolo m? No e continuano a essere sufficienti carta e matita e qualche dato che si trova dappertutto.

Eseguo solo una semplificazione (che potremmo anche non fare, ma la trattazione diventerebbe troppo lunga). Quando lavoravamo con i satelliti e Giove era più che sufficiente considerare i satelliti puntiformi rispetto al pianeta. Adesso, la situazione è leggermente diversa, dato che i diametri dei satelliti sono comparabili. Tuttavia, le distanze tra di loro sono sempre grandi rispetto al diametro e quindi gli angoli molto piccoli. Lasciatemi, perciò, continuare a considerare il satellite che deve transitare  davanti all’altro come puntiforme. Ossia, sostituisco la linea verde continua del riquadro con quella verde tratteggiata. E’ una semplificazione che ci permette di non considerare la doppia tangenza tra i due satelliti. Basterebbe cambiare un pochino la formula che ci permette di calcolare m, ma non ne vale la pena. Oltretutto, come si vede chiaramente, il nuovo angolo che trovo è più piccolo di m e quindi non faccio altro che limitare le possibilità di visibilità del transito. Insomma, vi regalo una sicurezza ancora maggiore! Non preoccupatevi, però. Come già detto, gli angoli sono piccoli e sono talmente tanti i parametri che non possiamo considerare (eccentricità dell’orbita gioviana, piani orbitali dei satelliti non perfettamente complanari, ecc.) che questa semplificazione non cambia il risultato concettuale. Tanto, come ormai sappiamo bene, l’importante è dare al computer l’idea di base. Lui sarà capace di tenere in conto tutte le sfumature. Se non fosse così perché avremmo mai dovuto inventarlo? Non certo solo per usare facebook o twitter…

Disegniamo, allora, la Fig. 21 Come vedete è perfettamente identica alla Fig. 4 (seconda parte). Vi è sempre un triangolo rettangolo e il seno dell’angolo m vale sempre il rapporto tra raggio e distanza. Trovate qualche difficoltà supplementare? Direi proprio di no. Non abbiamo fatto altro che sostituire Giove (o la stella) con un satellite e la distanza Giove-satellite (o stella-pianeta) con la distanza satellite-satellite. Elementare, Watson!

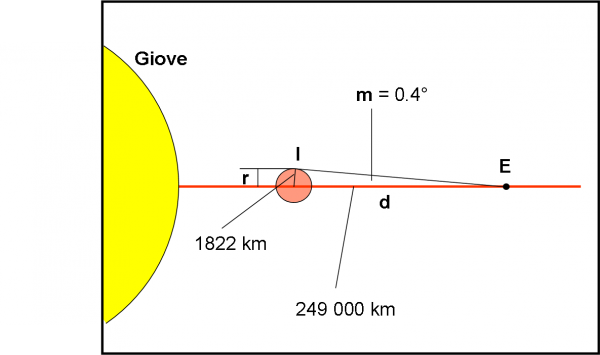
Consideriamo, ad esempio, i primi due satelliti medicei: Io (I) ed Europa (E). Ho considerato loro perché sono i più vicini e quindi danno anche l’angolo m più grande. Se il Sole ha una declinazione satellicentrica (che è però anche Giovicentrica dato che i satelliti risiedono sul piano equatoriale di Giove) inferiore a questo valore “massimo” dell’angolo limite, vi è transito mutuo tra i due satelliti.  Potremmo fare i calcoli per tutte le coppie e per tutte le possibili configurazioni di allineamento (divertitevi…). Nel caso della figura si ottiene un angolo m = 0.4°. Beh… c’era da aspettarselo, dato che le condizioni diventano molto più restrittive.

A questo punto potremmo nuovamente descrivere i paralleli azzurri per ogni coppia di satelliti e via dicendo. Ma, ormai, sappiamo bene come fare (basta seguire le figure del capitolo scorso con i nuovi risultati). Vedremmo che il Sole sta quasi sempre al di sopra dei paralleli azzurri e quindi non riesce ad assistere ai transiti con continuità. Nessun problema, basta aspettare… i nodi non tradiscono mai!

Passiamo subito all’ultima figura che descrive sinteticamente e quantitativamente la visibilità da parte del Sole. Mi riferisco a quella che riporta la declinazione solare giovicentrica in funzione del tempo (Fig. 17, quarta parte). Può bastare ritoccarla un po’ e il gioco è fatto, come mostra la Fig. 22. Il percorso del Sole è sempre lo stesso. Dobbiamo solo aggiungere la fascia verde che indica la zona in cui il Sole vedrebbe almeno un transito (in particolare, quello tra Europa e Io, pari a una declinazione limite di 0.4°). Sicuramente le cose sono cambiate e il Sole entra nella fascia quando arriva piuttosto vicino ai nodi, ossia quando assume una declinazione prossima a zero (equatore visto di taglio).

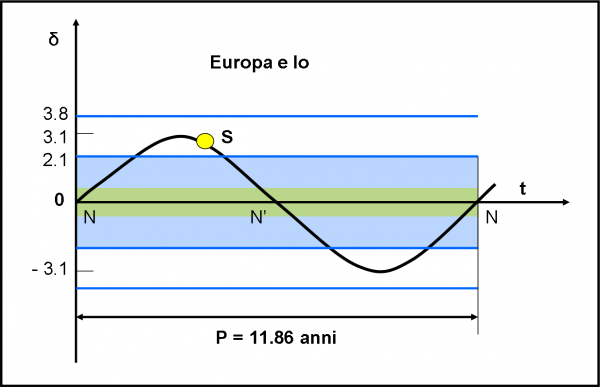
Ricordiamo, ancora, che i nodi dividono a metà il percorso completo del Sole. Dato che il Sole impiega 11.86 anni a girare attorno a Giove (o il viceversa, ma è lo stesso), ne segue che i transiti mutui tra satelliti avvengono circa ogni 11.86/2  = 5.93 anni. Dato che si ha un certo margine prima e dopo i nodi, non è certo sbagliato concludere che avvengono in media ogni sei anni circa.

Finora, abbiamo studiato le varie situazioni guardando le configurazioni in un piano perpendicolare a quello dell’equatore e dell’orbita di Giove. Quando parlavamo di transito di un satellite davanti a Giove, non vi era nemmeno bisogno di vedere le cose “dall’alto” o “dal basso” (avremmo solo capito quanto sarebbe durato il transito). Per i transiti mutui dei satelliti è invece molto più istruttivo, dato che essi orbitano attorno a Giove con periodi diversi tra loro e quindi danno luogo a configurazioni abbastanza variegate. Una precisazione ovvia, ma che non fa mai male. Il Sole si muove lungo la sua traiettoria molto lentamente e quindi una sua posizione favorevole nella Fig. 22 vuole dire regalare un’ampia possibilità ai satelliti per girare attorno a Giove, dato che i loro periodi orbitali vanno da poco più di uno a poco meno di diciassette giorni. In altre parole, il Sole aspetta che i satelliti giochino a nascondino.

Vale, quindi, la pena di mostrare ciò che capita guardando tutto perpendicolarmente all’equatore di Giove, ossia proiettando il tutto su di esso. Vediamo qualche caso, relativo a soli due satelliti, nella Fig. 23. Le due linee verdi delimitano la zona in cui possono avvenire i transiti. Come si nota si possono avere transiti di 1 davanti a 2 (1’ e 2’oppure 1 e 2’) o di 2 davanti a 1 (2 e 1’ oppure 2 e 1).

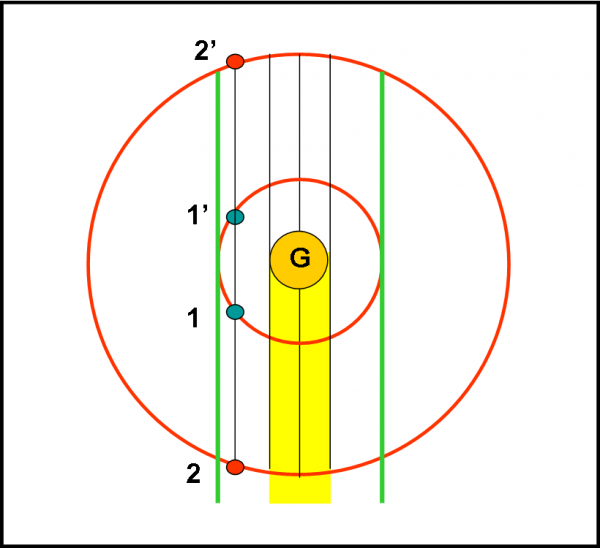
Il successo dei transiti dipende, però, anche dalla configurazione verticale (quella maggiormente utilizzata finora) e dai valori dei periodi di rivoluzione dei satelliti. Insomma, la soluzione esatta ci sarà data nuovamente dal calcolatore. Ma noi sappiamo benissimo cosa succede e questo è l’importante. Se poi vogliamo anche simulare la situazione con un programma “pappa pronta” possiamo anche farlo, dato che ormai abbiamo capito il gioco.

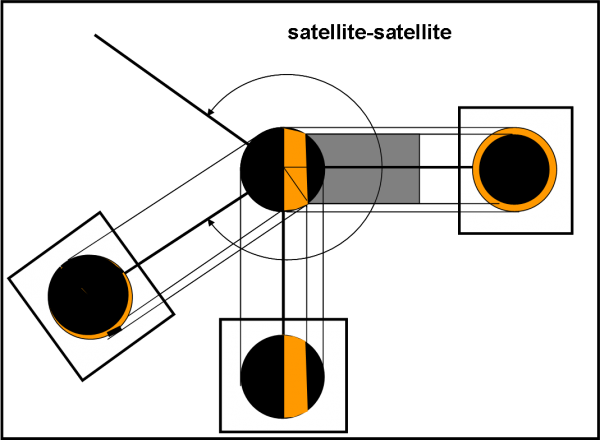
A questo punto, possiamo pure fare accendere la luce al nostro Super Kepler e dare al Sole quello che è del Sole. I vari transiti diventano immediatamente eclissi mutue tra i satelliti. Non ci rimane che calcolare chi li può vedere. Non cambia niente rispetto al problema Giove-satellite. Anzi, gli spettatori possono anche disporsi in posizioni più defilate. Infatti, l’ombra proiettata su un satellite da un  altro non sarà effettivamente un punto, ma un disco piuttosto grande, magari il cilindro d’ombra è perfino superiore al disco colpito. Ne segue che si estende il campo di visibilità, come mostra la Fig. 24, analoga alla Fig. 19 (quarta parte). Si notano eclissi anulari, strisce luminose e magari anche “buio totale”,  dato che il satellite investito dall’ombra è più piccolo del cilindro d’ombra (eclissi totale di Sole). Lascio a voi studiare bene la figura e le altre possibilità. Ormai è un gioco da ragazzi…

Abbiamo risolto tutti i casi di eclissi. Dobbiamo dire grazie al Super Kepler Sole, una sonda perfetta.

L’appetito, però, vien mangiando. E se cambiassimo sonda? Visto che abitiamo sulla Terra, perché non considerare proprio lei come Super Kepler? Otterremo lo stesso risultato? Purtroppo no. Per due motivi: innanzitutto perché la Terra non si può accendere e deve accontentarsi di vedere i transiti (osservatore passivo). Un fenomeno, quello dei transiti, che è del tutto “soggettivo”, dato che nessun altro può vederlo in giro per lo Spazio, tranne casi estremamente particolari. Cosa, però, ancora più importante è che la Terra non gira intorno a Giove, ma intorno al Sole. E questo complica un po’ la situazione. Chiedetelo a Tolomeo e ai suoi epicicli che cercavano di spiegare il movimento di un Giove che doveva assolutamente girare (quasi) attorno alla Terra.

La risolveremo la prossima volta… che sarà anche l’ultima!