Bene, siamo pronti a far cadere la … Luna? Purtroppo, sì e … no. Insomma, mi sono accorto che era meglio affrontare il problema sia arrivando “da fuori” che “da dentro”. Questa puntata racconta il primo metodo…

Una descrizione senza volere sapere il perché

Ancora prima, però, dobbiamo imparare a descrivere un moto a cui sono soggetti moltissimi corpi celesti (la nostra “casa” per prima). Attenzione, però: descriviamo solo il moto senza voler sapere chi o cosa lo causi e perché. Ci limitiamo a fare cinematica, ossia descrizione. Non parliamo ancora di vittime, sicari e mandanti. Facciamo solo una banale descrizione basata sulle definizioni di velocità e accelerazione e sui loro legami con la traiettoria descritta. Lasciamo quindi da parte l’inerzia del corpo e la sua voglia di reagire, di difendersi e di fare vendetta.

Ciò che stiamo guardando dal nostro sistema di riferimento inerziale è solo e soltanto un fenomeno “asettico”, descritto da un punto senza massa. Questo moto è molto simpatico, perché è ripetitivo e continuo e quindi la situazione da studiare è sempre la stessa. Lo possiamo studiare molto semplicemente.

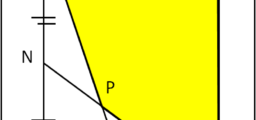
Ciò che osserviamo (Fig. 6) è un punto P che si muove attorno a un punto C mantenendo sempre la stessa distanza R. Beh… non ci vuole molto a capire che stiamo guardando un moto circolare. Non solo, però. Ci accorgiamo anche che la velocità del punto è uniforme. Come possiamo renderci conto di questo fatto? Beh, basta notare che l’angolo (o l’arco) descritto dal raggio R (o dal punto P) è sempre lo stesso per intervalli di tempo costanti.

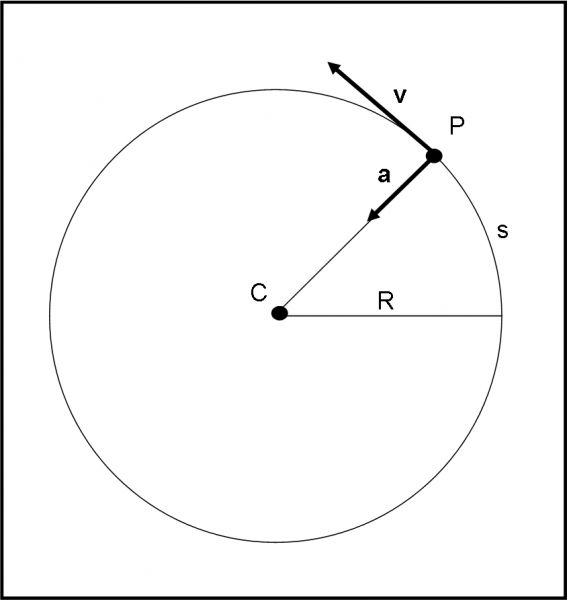
Senza sapere ancora scrivere le formule relative al moto, possiamo già enunciare alcuni dati di fatto che abbiamo imparato a conoscere nei primi due capitoli. La velocità del punto è sempre tangente alla circonferenza. Tuttavia, dato che cambia continuamente direzione deve esistere un’accelerazione centripeta che regoli questo continuo spostamento della direzione. Infine, non deve esistere alcun accelerazione tangenziale dato che il modulo della velocità rimane costante.

Cosa possiamo concludere da queste semplici constatazioni? Che un punto può permettersi di girare in modo indefinito a velocità costante attorno a un altro punto, mantenendo da lui sempre la stessa distanza, solo se esiste in  ogni punto della traiettoria un’accelerazione centripeta, ossia diretta verso il centro del cerchio osculatore, che, però, in questo caso è sempre lo stesso ed è proprio definito, in ogni punto, dal cerchio su cui il punto descrive il moto. Veramente una situazione semplicissima.

Quanto vale la velocità del punto P? Non è certo difficile ricavarla da una semplicissima considerazione. Posso misurare il tempo T che è necessario affinché il punto P compia un giro completo attorno a C. Che percorso descrive il punto P? Beh… è ovvio, la circonferenza, ossia 2πR. Ora basta chiedersi quale tratto ds della circonferenza descrive nell’intervallo di tempo dt, attraverso la proporzione:

2πR : T = ds : dt

Ossia

ds/dt = 2πR/T

Ormai siamo esperti e sappiamo benissimo che scrivere ds/dt vuole dire scrivere il modulo della velocità, costante per definizione, quindi:

v = 2πR/T

A questo punto, non abbiamo nemmeno bisogno di usare triangoli e/o segmenti vari, dato che sappiamo già bene quanto vale l’accelerazione centripeta che fa variare la direzione della velocità punto per punto. L’abbiamo ricavata la volta scorsa in due modi (ho scovato anche un terzo modo che prima o poi vi descriverò!) Essa vale, in modulo:

a_C = v²/R   …. (1)

Dato che la traiettoria è una circonferenza anche l’accelerazione deve essere una costante, come d’altra parte è dimostrato dalla formula precedente che dipende da v (costante) e da R (costante).

Cosa possiamo concludere? Che stiamo guardando un moto estremamente semplice in cui vi è un punto che, per potersi muovere di moto circolare uniforme attorno a un punto C, deve subire costantemente un’accelerazione centripeta che è legata alla velocità v del punto P dalla relazione (1).

Cosa vuol dire tutto ciò? Che, ad esempio, se la velocità aumentasse, dovrebbe aumentare anche l’accelerazione centripeta. O, inversamente, se aumentasse l’accelerazione centripeta dovrebbe aumentare la velocità del punto P. Un perfetto gioco di squadra. Sembra che il  “crimine” nascosto si risolva in una reciproca pacifica convivenza.

Per un osservatore esterno, in un sistema inerziale, la faccenda è di una semplicità incredibile. Basta misurare il periodo di rivoluzione e la distanza tra C e P (costante) è ogni grandezza in gioco è completamente individuata. Attenzione, però, che per poter arrivare a questa conclusione è stato necessario imparare come calcolare l’accelerazione in grado di causare un moto curvilineo.

Purtroppo, questa è una visione molto superficiale, che descrive, ma non si chiede il perché e il come. Non può quindi accorgersi del dramma che si nasconde dietro a una “danza” regolare e senza fine.

Una ragnatela costruita a regola d’arte

Lasciamo quindi da parte la cinematica (ci servirà dopo) che, malgrado sia  un modo apparentemente semplicistico di valutare i fenomeni, è utilissima e fondamentale, e diamo al punto P una sua concretezza fisica. In parole povere, diamogli una massa, ossia un’inerzia tale da farlo muovere di moto rettilineo uniforme rispetto al nostro sistema di riferimento. Il punto di massa m se ne andrebbe per i fatti suoi, ma ecco che cade nella “tela di un ragno”. Parlo di tela di un ragno, ma non deve essere considerata una delle mie solite similitudini “poetiche”. Senza che il nostro corpo di massa m lo sappia, non troppo lontano da lui, vi è un corpo O di massa M ben maggiore, che ha proprio steso la sua rete attorno a lui.

Che tipo di rete è? Una rete “vettoriale”! In particolare, una rete composta da infinite accelerazioni pronte ad agire sul malcapitato che ha la sventura di entrarci dentro. La forza che O esercita si traduce in una rete di sicari in attesa di una vittima.  Che tipo di forza può possedere un corpo di massa M, tale che possa agire anche a distanza, ossia senza nemmeno toccare la vittima? Beh… ha un nome ben conosciuto: gravità. Essa viene definita attraverso una formula che è uno dei capolavori della fisica descritta dall’uomo. Descriviamola a parole e poi attraverso la matematica. Ogni corpo di massa M esercita una forza su un corpo di massa m che è data dal prodotto tra le due masse diviso il quadrato della reciproca distanza.

F = GMm/r²  …. (2)

Ovviamente, per il terzo principio della dinamica, se M esercita una forza su m, anche m deve esercitare una forza uguale contraria su M. La prima agisce su m, la seconda su M. Fate molta attenzione a questa frase, perché verrà utile quando comparirà la forza centrifuga.

Nel nostro caso, però, chi comanda il gioco è M, mentre m subisce. La sua reazione, ossia la sua vendetta, è cosa veramente ridicola… In realtà, la forza è la stessa, ma può fare ben poco su una massa come M. Ricordate cosa abbiamo detto nelle altre puntate? Vediamo, allora, come è stato predisposta la ragnatela di O.

Innanzitutto, dobbiamo tener conto del secondo principio della dinamica, che abbiamo ricavato abbastanza facilmente. Esso dice:

F = m a   …. (3)

La formula è già stata investigata in lungo e in  largo e sappiamo che può esprimersi, tra l’altro, con la frase: l’accelerazione causata da F è “regolata” da m, ossia dalla pigrizia di P a cambiare il proprio movimento. La F che compare nella (2) e nella (3) è la stessa, ossia la forza del “ragno” O. Basta uguagliarle e ricaviamo immediatamente:

GMm/r² = ma

Semplificando la massa m, si ricava immediatamente l’accelerazione che agisce su di lei, ossia il sicario predisposto da O. Si ha che:

a = GM/r²   …. (4)

La costruzione della ragnatela, composta da tutte le accelerazioni che aspettano m al varco, diventa, allora, cosa banale ed è rappresentata in Fig. 7.

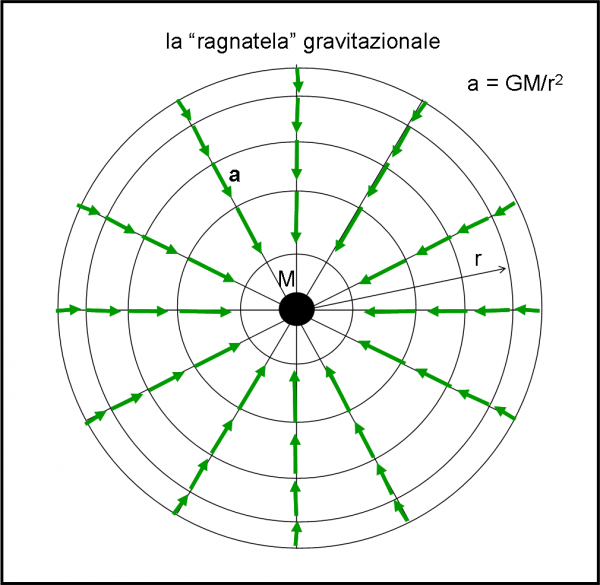
In ogni punto dello spazio attorno al “ragno” O, si può inserire un sicario accelerazione che non aspetta altro che far deviare l’ignaro corpo P. La potenza del sicario dipende solo dalla distanza rispetto al ragno. Più si è lontani dal mandante e meno efficace è l’azione del sicario. Cosa cerca di fare ogni sicario? Solo e soltanto attirare la vittima verso il ragno. L’accelerazione è quindi diretta verso il corpo O. E’ facilissimo disegnare questa ragnatela, che NON dipende da quanto vale la massa m che vi cade dentro e che perde di vigore spostandosi verso l’esterno. A ogni punto si associa un vettore accelerazione a, di modulo (4) e diretto verso O. Esso rappresenta l’azione del sicario, ossia l’operazione di spostarlo verso il centro. La ragnatela prende il nome di campo gravitazionale del corpo O di massa M.

Piuma o macigno per me pari sono

Ribadiamo ancora (è troppo importante) che il valore dell’accelerazione, ossia della capacità di spostare una certo corpo P, di massa m, verso O è INDIPENDENTE dalla massa m. Il che vuole anche dire che qualsiasi corpo capiti nella rete subisce la stessa accelerazione verso O, a parità di distanza da O. Lasciatemi, quindi, enunciare un fatto importantissimo che Galileo Galilei ha cercato di dimostrare in tutti i modi. Se facciamo cadere verso la Terra un macigno di molte tonnellate e una piuma leggerissima, esse sono soggette alla stessa accelerazione e quindi, senza attriti o altre cose del genere, cadono al suolo con la stessa velocità.

Immaginate, infatti, di portare a una certa altezza h sia il macigno che la piuma. Essi hanno velocità ZERO rispetto al suolo perché li teniamo fermi. Poi li lasciamo liberi di subire la forza del ragno O (la Terra). Essendo alla stessa distanza da lui, l’accelerazione, ossia la variazione della loro velocità, è la stessa, indipendentemente dalla massa che hanno. Essi partono con v₀ = 0, al momento t₀ = 0 e quindi, dopo un certo intervallo di tempo, i due corpi acquistano la stessa velocità istantanea v = v₀ + dv = dv, dato che dv è dettato dalla stessa accelerazione (dv/dt = a). I due corpi cadono alla stessa velocità verso il ragno, indipendentemente dalla loro massa. Risultato sicuramente contro intuitivo, ma dimostrabile in modo facilissimo e impeccabile. Se non vi piace… prendetevela con la forza gravitazionale!

Vale la pena chiarire una frase che ho letto spesso in giro e che è fondamentalmente errata. Si dice che la caduta di due gravi  di massa diversa avviene alla stessa velocità, dato che l’accelerazione di gravità è costante (la famosa g). Non è assolutamente vero! Il fatto che g (ossia GM/R²) possa essere considerata costante nelle vicinanze della Terra è un’approssimazione più che plausibile (la distanza dal centro della Terra è praticamente sempre la stessa), ma questa semplificazione fa solo sì che il moto verso il suolo possa considerarsi uniformemente accelerato (ossia ad accelerazione costante), ma non è certo una condizione per ottenere una identica velocità di caduta. Se lasciassimo cadere gli oggetti da un’altezza enormemente più grande, benché l’accelerazione non potrebbe più essere considerata costante, le velocità di caduta dei due corpi di massa diversa sarebbero comunque identiche. E’ bene smentire subito false conclusioni…

Come districarsi nella ragnatela

Torniamo alla ragnatela e vediamo come riesce ad agire su un corpo P che non parte da fermo ma che è -ovviamente- in moto rettilineo uniforme rispetto al nostro sistema inerziale (primo principio della dinamica).

Potremmo scrivere subito le condizioni che permettono al corpo P di seguire perfettamente un moto circolare uniforme attorno a O. Sappiamo, infatti, benissimo di cosa abbiamo bisogno, ricordando la descrizione cinematica. Di solito si fa così e lo farò anch’io, ma prima voglio farvi vedere cosa succede realmente durante l’avvicinamento di P a O. Si capiranno meglio le condizioni favorevoli per ottenere una specie di “stallo”, ossia una parità tra i due corpi in gioco.

Sappiamo che quello di massa minore deve subire la forza di quello più grande (malgrado cerchi di vendicarsi, come vedremo a tempo debito) o -meglio- dei suoi sicari sparsi per lo spazio. Tuttavia, per certi valori della velocità e dell’accelerazione, si potrebbe ottenere una specie di pareggio. Qualcosa di simile a uno stallo nel gioco di scacchi. Magari un giocatore è ridotto al lumicino, mentre l’altro è ancora pieno di pezzi importanti. Sebbene risulti chiara la maggiore “potenza” del secondo, il primo potrebbe trovare una situazione di ripiego, ossia trovare lo stallo. E’ chiaramente in netta inferiorità, ma il suo Re riesce a evitare lo scacco matto e può sopravvivere per sempre, adattandosi alla configurazione raggiunta. La partita, benché “ai punti”, sembrerebbe stravinta dal secondo giocatore, ma DEVE essere, invece,  dichiara “patta”. Non esiste un vincitore ufficiale.

La stessa cosa capita al nostro corpo P. Esso, volente o nolente, subisce l’accelerazione del corpo più massiccio O. Un’accelerazione diretta verso di lui, con lo scopo (non certo misterioso) di far cadere P su O. Tuttavia, malgrado sia in balia di questa accelerazione, la velocità v del corpo P può riuscire ad arrivare a uno stallo. Anzi, se essa fosse sufficientemente alta e diretta nel modo giusto, P potrebbe anche sopravvivere e andarsene per la sua strada, vincendo addirittura la sfida. Una vittoria molto dura, dato che è stato costretto, comunque, a cambiare il suo moto rettilineo uniforme. A noi interessa, soprattutto, la situazione di stallo, ma vale la pena cercare di analizzare anche le altre due (più comuni) soluzioni: quella della fuga e quella della caduta catastrofica.

Vi prego di notare, ancora una volta, che in tutto questo gioco la massa m non compare per niente, dato che la ragnatela non si cura di lei e agisce comunque. Questa è una caratteristica del campo gravitazionale e non certo di tutte le forze della Natura. Ricordiamocelo bene. Tuttavia, non è un risultato veramente strano. In  realtà, la massa m, anche se non si vede, svolge il suo compito, dato che il confronto tra forza gravitazionale e inerzia del corpo continua implacabile. L’accelerazione sicario si è “ridotta” a quella che conosciamo, proprio perché la massa m è scomparsa per dar luogo all’accelerazione di gravità. Anche se non si vede, la massa m esiste e come. Se non avesse massa, il corpo P non subirebbe la gravità di O.

Giochiamo con i vettori

Questo paragrafo può essere saltato da chi vuole andare al sodo e non vuole perdere tempo a cercare di rappresentare il “dramma” che si svolge tra il corpo P e la ragnatela. In altre parole, da chi vuole subito studiare il moto circolare uniforme, ossia la posizione di “stallo”. Chi invece vuole divertirsi con un "filmato" molto grossolano di ciò che capita durante tutto il passaggio del corpo P attraverso la ragnatela di O, alzi le antenne e mi segua!

Immaginiamo un corpo P che viaggia tranquillo lungo la sua traiettoria rettilinea uniforme con una velocità v costante in modulo e direzione. Il corpo O è ancora lontano e non si fa sentire. Tuttavia, posso usare la distanza tra P e O per definire la velocità. Infatti, le distanze tra O e due punti P1 e P2 possono essere considerati dei vettori e la loro differenza (vettoriale) ci fornisce, come al solito, la direzione della velocità. Seguiamo questa prima fase nella Fig. 8.

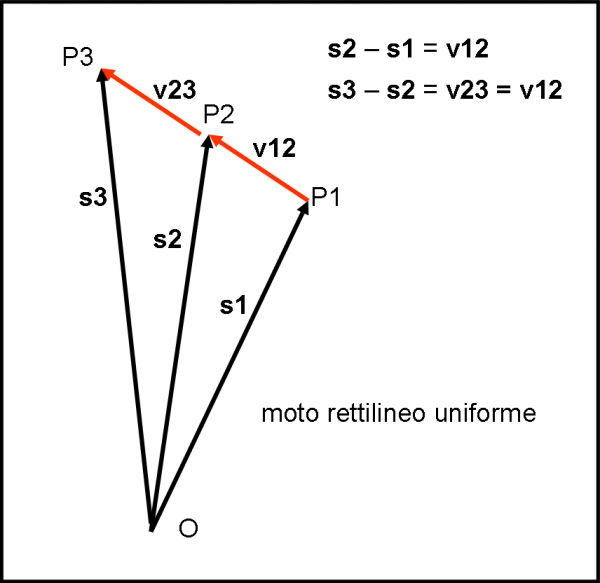
Vale la ovvia relazione:

v12 = ds12/dt = (s2 – s1)/dt

Posso, però, eseguire ancora una semplificazione: prendere dt = 1 (basta scegliere la giusta unità di misura). In questo modo considero lo spostamento dal punto P1 a P2 uguale alla velocità del corpo tra P1 e P2. In altre parole, data la velocità nel tratto P1 - P2, posso disegnare immediatamente la posizione del punto P2. Dato che ripetersi non fa mai male, riscriviamo la relazione che spiega direttamente  la procedura da seguire:

v12 = s2 – s1

O, se preferite:

s2 = s1 + v12

Conoscendo la velocità v12 e la posizione P1 (data da s1), trovo immediatamente la posizione s2 e quindi la posizione P2, attraverso una somma vettoriale.

Come già detto, finché la ragnatela non entra in azione, la semplificazione non crea assolutamente problemi. Dato che la velocità è sempre la stessa, in modulo e direzione, considerare traiettorie rettilinee durante intervalli di tempo, piccoli o grandi che siano, non cambia il risultato. In altre parole, la lunghezza e la direzione dello spostamento del corpo, nell’intervallo  dt = 1, può benissimo essere considerato uguale alla velocità del corpo.

Noi, però, continueremo a usare lo stesso approccio anche quando v comincerà a cambiare, sia in direzione che modulo. Avremo un insieme di tratti rettilinei continui che indicheranno  “approssimativamente” la traiettoria seguita dal corpo P.

Spieghiamo come fare. Il punto P di massa m, entra, finalmente, nella ragnatela. Rappresentiamo il suo limite esterno come un cerchio di raggio R. Prima approssimazione! La ragnatela non comincia a un raggio preciso, ma si estende fino all’infinito, diventando sempre meno attiva. Noi, però, la facciamo entrare in azione in modo improvviso.

Consideriamo la Fig. 9.

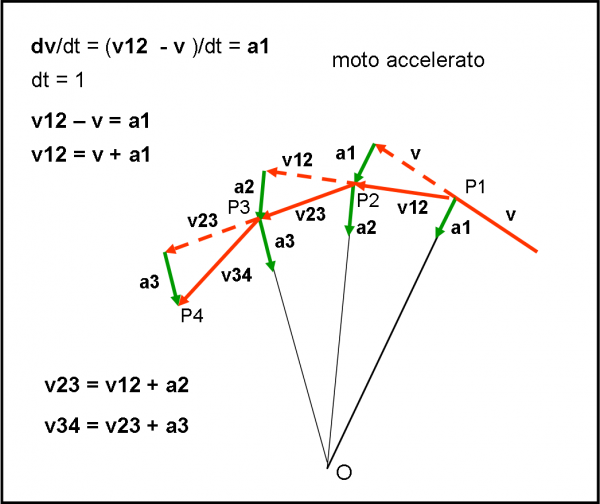
In P1 entra in azione l’accelerazione di gravità a1, che tende ad attirare il corpo P verso O. La velocità v, costante e tranquilla, subisce uno spostamento nel tragitto da P1 a P2 e diventa v12. Questo spostamento è proprio comandato dall’accelerazione subita in P1 che vale:

a1 = dv/dt = (v12 – v)/dt

ma, avendo posto dt = 1, abbiamo anche:

a1 = v12 – v

Conoscendo la v precedente e la a1 (la ragnatela), posso disegnare subito la v12, in direzione, intensità e verso, attraverso la regola del parallelogramma (attenzione: sto sommando o sottraendo dei vettori e non dei moduli!), dato che:

v12 = v + a1

Dato che dt = 1, il tragitto percorso dal corpo P può essere approssimato dalla nuova velocità v12 (come fatto fuori dalla ragnatela) e quindi di determina subito P2.

Occhio, però, che stiamo facendo differenze di vettori e non di moduli di vettori! Il modulo della velocità è uguale al modulo del vettore somma (o differenza) e NON è uguale alla differenza dei moduli dei vettori.

Non è difficile continuare il nostro gioco dinamico. In P2 il corpo subisce una nuova accelerazione  a2 che è maggiore di quella precedente, dato che il corpo si è avvicinato a O: la ragnatela acquista potenza. Come faccio a trovare la nuova velocità v23 e il punto P3? Basta rifare il procedimento di prima, dato che:

v23 = v12 + a2

E via dicendo…

In questo modo  possiamo descrivere la traiettoria del corpo P sotto l’effetto del campo gravitazionale di O, ossia della sua ragnatela. Quello che stiamo eseguendo è comunque solo una specie di gioco, dato che ha un senso compiuto solo finché la velocità resta costante. Quando inizia a variare dovrei considerare dei tratti curvilinei piccolissimi, mentre, invece, continuiamo a usare tratti rettilinei tra i punti raggiunti (prendendoli anche molto grandi). Teniamo quindi ben presente che è un gioco valido in prima approssimazione! Comunque, più si restringe l’intervallo degli spostamenti e più ci si avvicina alla realtà. Nelle figure precedenti ho allungato il vettore accelerazione "a occhio" e senza seguire la formula che ne determina il modulo (GM/r²). Le figure precedenti e soprattutto quelle che seguono vanno, quindi, prese solo come indicative, mi raccomando…

Facciamo tre esempi veramente “brutali”, ma chi vuole può divertirsi a stringere gli intervalli e a variare velocità e accelerazioni a piacere. Notate che ho anche descritto in questo modo così “infantile” anche una traiettorie a spirale attorno al corpo O, come capita attorno ai buchi neri, o attorno a una stella che mangia la materia della compagna. Io, adesso, ve li mostro e poi voi potrete divertirvi a piacere (anche trovare l’effetto fionda…).

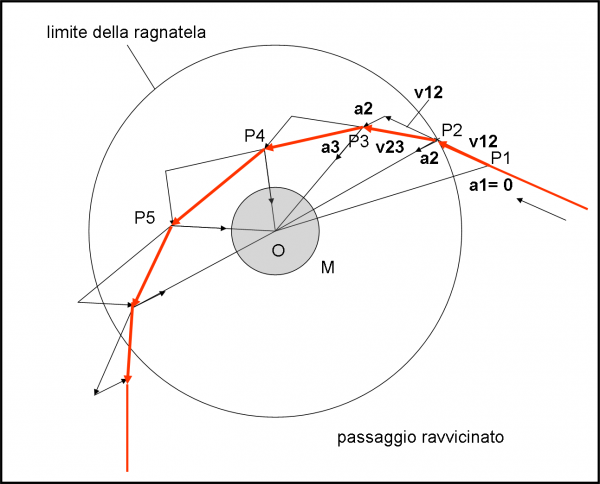
In Fig. 10, la velocità iniziale del corpo ha una direzione e un'intensità tali da superare l’attrazione di O. Alla fine, il corpo P, dopo essere stato costretto a cambiare la traiettoria iniziale, esce dalla ragnatela e può tornare al suo moto rettilineo uniforme, anche se diverso da quello iniziale. Questo è il caso di un passaggio ravvicinato di un asteroide con la Terra. Nessun impatto, ma l’asteroide ha dovuto cambiare drasticamente traiettoria.

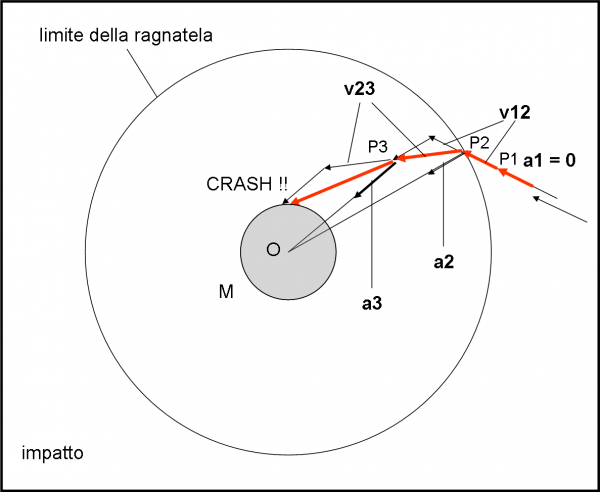
In Fig. 11, la velocità iniziale non riesce a controbattere l’accelerazione di gravità e il corpo non può fare altro che impattare velocemente su di esso.

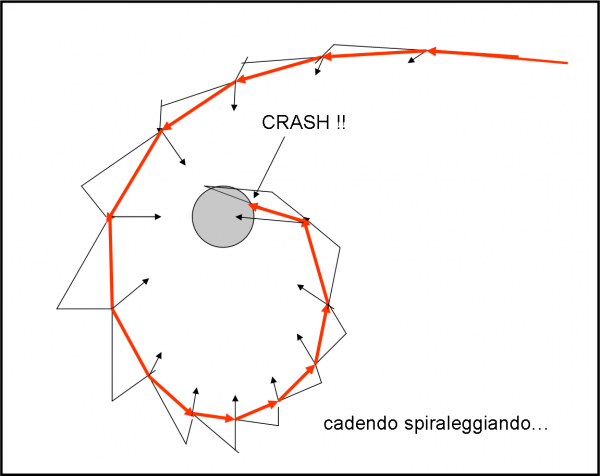
In Fig. 12, il gioco tra velocità iniziale e ragnatela ha uno svolgimento più lungo, una specie di tira e molla. Alla fine, vince l’accelerazione, ma si genera una bellissima traiettoria a spirale. Tenete presente che la distorsione della traiettoria dipende in gran parte dall’approssimazione brutale del metodo usato. Tuttavia, dà già un’idea della situazione piuttosto chiara e … divertente.

Nel fare qualche esercizio, ricordatevi che non basta il modulo della velocità per difendersi dalla gravitazione di O. Conta anche la sua direzione. Se la componente della velocità, nella direzione di O, ha lo stesso verso dell’accelerazione non fa altro che aiutare P a essere mangiato dal “ragno”. Se, invece, il verso è opposto, la lotta è molto più lunga e magari P riesce a vincere.

Se scegliete l’intervallino piccolo piccolo e una velocità abbastanza particolare, tale che diventi, a un certo istante, perfettamente perpendicolare alla congiungente P con O, otterrete anche che l’accelerazione è TUTTA perpendicolare alla velocità. Cambierebbe la direzione della velocità, ma non il modulo. Questa situazione la conosciamo molto bene dalla cinematica del moto circolare uniforme! Il corpo P ha ottenuto lo stallo e si mette in orbita attorno ad O. Ovviamente, lo può fare a qualsiasi distanza da O, sempre che il modulo e direzione della sua velocità siano quelli giusti. Sappiamo, infatti, benissimo come i moduli di velocità e accelerazione devono essere legati tra loro: ce lo dice la (1), ossia:

a_C = v₀²/r

da cui si ricava immediatamente il valore di v₀, capace di mantenere il corpo P in moto circolare uniforme attorno ad O.

v₀ = (a_C r)^1/2

Ma noi conosciamo benissimo il modulo della a_C, dato che si ricava dalla ragnatela, ossia dal campo gravitazionale di O. Esso vale:

a_C = GM/r²

Sostituendo:

v₀ = (GMr/r²)^1/2

E, infine:

v₀ = (GM/r)^1/2    …. (5)

Ho lavorato con i moduli, dato che so benissimo che il vettore è tangente in ogni punto al cerchio di raggio r.

Stallo!

Trascurando del tutto il racconto del dramma, possiamo arrivare subito al caso di stallo, ossia a quando la velocità del corpo che giunge sulla tela del ragno è tale da immetterlo su un’orbita circolare, dove può muoversi di moto circolare uniforme attorno a O. Quali sono le condizioni particolari perché questo succeda? Le formule sono sempre le stesse. La variazione di velocità impartita dall’accelerazione di gravità deve avvenire solo  agendo sulla direzione e non sul modulo. Esattamente quello che avevamo visto trattando il moto circolare uniforme dal punto di vista cinematico. In altre parole, l’accelerazione, dovuta alla ragnatela, deve essere uguale all’accelerazione che si ha in un moto circolare uniforme. Ciò capita per una certa distanza r di P rispetto a O. La prima vale GM/r², la seconda v²/r. Basta uguagliare e si ottiene:

GM/r² = v²/r

Semplificando:

v₀ = (GM/r)^1/2    …. (6)

Ovviamente, la (5) e la (6) sono identiche. La prima l’abbiamo ottenuta seguendo tutto lo svolgimento del crimine, la seconda cercando solo la posizione di “stallo”, di pareggio, di moto circolare uniforme.

Abbiamo comunque ricavato una relazione fondamentale. Affinché un corpo P si metta in orbita attorno a un corpo O di massa M, il modulo della sua velocità deve essere quello dato dalla (5) e la sua direzione deve essere perpendicolare alla direzione di O. In parole più tecniche: in ogni punto della traiettoria il cerchio osculatore deve rimanere sempre lo stesso e coincidere  con il cerchio di raggio R che ha per centro O.

Come vedete la (5) dipende dalla massa del corpo che ha creato la ragnatela, ma anche dalla distanza rispetto a lui. In altre parole, per entrare in orbita circolare (stallo), la velocità deve aumentare se la distanza r diminuisce. Più si va vicini a O e più grande è l’accelerazione che subisce P. Per riuscire a mantenersi in moto circolare uniforme deve aumentare la v₀. Teoricamente, perciò, se non vi fosse atmosfera o cose del genere, un corpo potrebbe ruotare intorno a un altro a qualsiasi distanza dalla massa centrale, sempre che abbia la giusta velocità.

Dall’esterno non è facile

Il moto circolare uniforme è perciò un caso estremamente fortunato per un corpo che arrivi dall’esterno rispetto alla ragnatela. Se la velocità di P fosse troppo alta e diretta in un certo modo, dopo una deviazione più o meno significativa della sua traiettoria, il corpo riuscirebbe a scappare e a tornare a un moto rettilineo uniforme. La velocità, infatti, cambierebbe solo durante l’azione dell’accelerazione di gravità, ma quando quest’ultima diventasse praticamente nulla, l’oggetto P tornerebbe alla sua situazione dominata solo dall’inerzia. Se, invece, la velocità fosse sempre troppo bassa e diretta in un certo modo, non potrebbe che cadere tragicamente su O.

E’ stato confermato ancora una volta il principio fondamentale. Chi comanda il movimento di un corpo è sempre e soltanto la velocità (non per niente è lo spazio percorso nell’unità di tempo). Chi può disturbarla, anche gravemente, è l’accelerazione, la sola che può agire su di lei, allungandola, accorciandola, piegandola. Una lotta tra una caratteristica insita nel corpo e un’azione comandata dal mandante. La vera sfida concettuale è tra le masse, ma la battaglia sul campo vede solo la vittima e il sicario.

Esiste un caso particolarissimo che ormai sappiamo inquadrare molto bene: La velocità del corpo P è ZERO rispetto al corpo O. L’accelerazione (anche se ha un valore costante g) ha gioco facile ad applicargli velocità via via crescenti fino a farla giungere ad O e schiantarsi. Un caso veramente eccezionale e irrealistico. Chi potrebbe mai avere velocità zero al momento dell’ingresso nella ragnatela? Doveva averla anche prima, ma allora non sarebbe mai arrivato fino alla ragnatela. No, un corpo che arriva dal “di fuori” deve comunque lottare e non può cadere come una mela! La Luna, se fosse arrivata da fuori, sarebbe potuta anche cadere, ma solo dopo una dura lotta tra i fili della ragnatela. Tuttavia, sappiamo benissimo che NON è caduta e nemmeno se n’è andata, per cui l’unico caso possibile è che sia riuscita a pareggiare la partita a scacchi, trovando lo stallo. Può anche essere, ma è un caso molto fortunato… forse troppo!

Due considerazioni rapide, rapide:

Dato che raggiungere la velocità necessaria al moto circolare uniforme è un caso fortunato, è molto difficile catturare un corpo vagante attraverso l’accelerazione gravitazionale. Il corpo, normalmente, o cade o fugge. Avremmo avuto bisogno di decine e decine di lune che avessero tentato l’aggancio e, alla fine, magari una ci sarebbe riuscita. Ma, trovare tanti oggetti delle dimensioni della Luna pronti a fare questa gara così vicine alla Terra, non era molto probabile nemmeno quando il Sistema Solare era molto più popolato e disordinato.

Teoricamente, sappiamo che la ragnatela stesa dal corpo O non ha mai fine e può arrivare ovunque nell’Universo. Un corpo P lontanissimo potrebbe, perciò, mettersi in orbita anche a distanza enorme da O. Sarebbe necessaria anche  una velocità v₀ molto bassa. Tuttavia, nello Spazio non esistono solo P e O, ma tantissimi altri corpi con le loro ragnatele. Ne segue che la somma di tutte queste, anche se molto  lontane, bastano e avanzano per trascinare via il corpo P dalla ragnatela di O, quando essa è ormai troppo debole.

Perché il Sole ci è riuscito?

Qualcuno potrebbe dirmi: “Ma come... dici che è praticamente impossibile essere immesso in un’orbita circolare attorno a O, e, invece, vediamo che i pianeti, e non solo, rivolvono tranquillamente attorno al Sole!”. La differenza fondamentale è che i pianeti si sono formati all’interno del disco che circondava la stella Sole, ossia i granelli di polvere che li hanno formati rivolvevano già attorno al Sole fin dalla nascita della stella. La velocità era già quella giusta! Se non fosse stata quella giusta, la polvere se ne sarebbe andata per sempre o sarebbe caduta sul Sole. Insomma, non sarebbe servita a formare i pianeti! In realtà ciò è parzialmente successo:  molta polvere del disco è finita realmente sul Sole o se ne è andata verso altre stelle.

In ogni modo, ovunque nel disco, sarebbe possibile, teoricamente, avere un corpo che gira attorno al Sole. Lo vediamo con gli asteroidi: si frantumano l’uno con l’altro, ma i loro frammenti continuano a stare in orbita, tranne casi particolari, dove subentra il caos dinamico… ma questa è un’altra storia, ben più complicata. Le velocità sono quelle giuste per restare nella ragnatela per tempi anche molto lunghi.

Ben diversa sarebbe la situazione se una stella arrivasse vicino al Sole. Ci sarebbe una lite furibonda, ma alla fine (dato che le velocità relative tra le stelle sono molto alte), se ne andrebbe facilmente per la sua strada. La stessa cosa capita per un meteoroide che si avvicina alla Terra. Tutto dipende dalla componente della velocità nella direzione della Terra, che si può sommare o sottrarre all’azione dell’accelerazione gravitazionale della Terra, aiutando la caduta se il verso è uguale o ostacolandola se il verso è opposto.

Insomma, ragazzi, la Luna non cade perché la sua velocità rispetto alla Terra soddisfa le condizioni di moto circolare uniforme. E’ caduta nella ragnatela e ha ottenuto uno stallo? Insomma, la Luna ha avuto (o forse ancora più la Terra) una fortuna enorme? Tutto è possibile nell’Universo, ma il troppo è troppo. Forse la Luna non è venuta dal “di fuori”, ma è partita dal “di dentro”.

In generale, però, tenete conto che stiamo parlando di velocità relative tra Terra e Luna. Entrambi i corpi ruotano attorno al Sole e quindi posseggono una certa velocità. Tuttavia, possiamo considerare, in prima approssimazione, che questo movimento comune sia rettilineo uniforme. Possiamo, perciò, cambiare tranquillamente il sistema di riferimento inerziale e sceglierne uno che viaggi alla velocità della Terra. Ne segue che la velocità “residua” della Luna è quella del satellite rispetto a noi. La stessa cosa che capita a una pietra lasciata cadere. Essa viaggia alla stessa velocità della Terra e quindi quando la lascio libera può considerarsi a velocità zero rispetto alla Terra e subisce senza pietà la sua accelerazione di gravità senza colpo ferire. Se invece la lancio per aria, prima di cadere descrive una certa traiettoria. Le ho impresso una certa velocità che, finché può, cerca di ribellarsi all’accelerazione di gravità. Questo caso particolare ci conduce a quel genio infinito di Newton e alla scoperta della legge di gravitazione universale. Come sotto prodotto, questo fenomeno ci porta alla formazione “endogena” della Luna, ossia dal “di dentro”, proprio come fosse una pietra lanciata verso lo spazio.

Mi spiace… ma devo fermarmi… la forza centrifuga deve ancora aspettare. Tuttavia, quel giochino di costruzione del moto all’interno della ragnatela  mi piaceva troppo e spero che lo apprezziate anche voi.

Alla prossima, sperando che sia l’ultima, ma temo di no, dato che vorrei fare qualche giretto in … giostra!

P.S.: Prima che qualcuno me lo chieda... Ho sempre parlato di moto circolare uniforme e mai di orbite ellittiche. La legge di gravitazione rimane la stessa e i risultati non cambiano assolutamente. Cambiano, invece, i passaggi matematici e i vettori si ingarbugliano ancora di più. Insomma, vi prego di fidarvi e di non pretendere una trattazione completa. Invece di cinque articoli, o quello che sarà, ne avremmo bisogno di ... 50!