Categorie: Matematica
Tags: cubica flessi ascendenti flessi discendenti flessi obliqui
Scritto da: Vincenzo Zappalà
Commenti:16
30. Esercizi sulle cubiche incomplete **
Per verificare che tutto sia stato compreso, facciamo un paio di esempi pratici: uno con soluzioni reali dell’annullamento della derivata prima e uno con soluzioni immaginarie. Esempi molto utili anche per chiarire meglio le idee sui flessi ascendenti e discendenti.
Il primo esempio deve avere a e c di segno diverso…
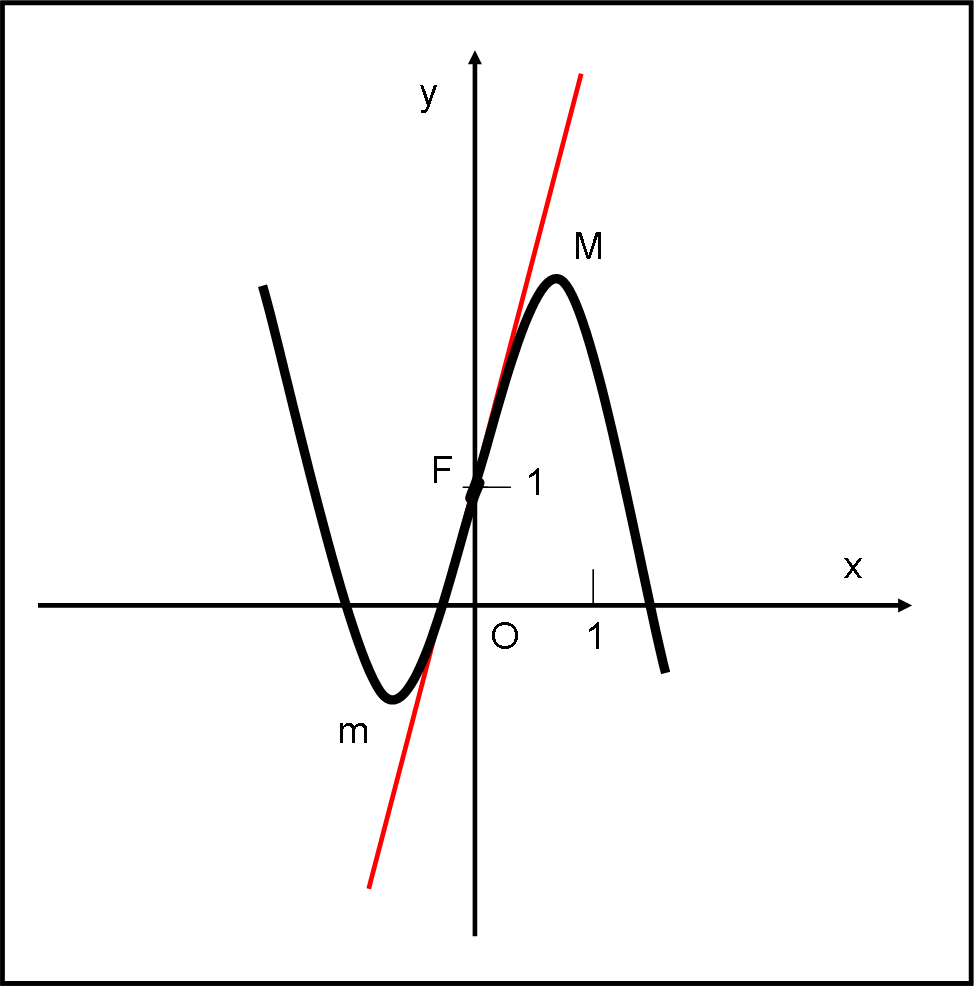
y = - 3x3 +4x + 1
Calcoliamo e annulliamo la derivata prima
y’ = - 9x2 + 4 = 0
9x2 = 4
x2 = 4/9
x1,2 = +/- (4/9)1/2 = +/- 2/3
Controlliamo se la formula generale data precedentemente verifica questo risultato
x1,2 = +/- (- c/3a)1/2 = +/- (- 4/- 9)1/2 = +/- 2/3 perfetto!
Facciamo in fretta a sapere se sono di massimo e/o di minimo dal segno della derivata seconda calcolata per loro.
y” = - 18 x
per x1 = 2/3 si ha
y”(2/3) = - 18(2/3) = - 36/3 = - 12
E’ negativa e quindi è un punto di massimo.
Per x2 = - 2/3 si ha
y”(- 2/3) = -18(- 2/3) = 12
E’ positiva e quindi è un punto di minimo.
Anche questi valori sono soddisfatti dalla formula generale (e ci mancherebbe altro…)
Calcoliamo le ordinate dei punti di minimo e di massimo
y = - 3x3 + 4x + 1
y1 = - 3(2/3)3 + 4 (2/3) + 1 = - 8/9 + 8/3 + 1 = (- 8 + 24 + 9)/9 = 25/9
y2 = - 3 (- 2/3)3 + 4(- 2/3) + 1 = 8/9 – 8/3 + 1 = (8 – 24 + 9)/9 = - 7/9
Ricapitolando:
il punto P(- 2/3, - 7/9) è un punto di minimo
il punto Q(2/3, 25/9) è un punto di massimo.
Troviamo, ora, il punto di flesso obliquo.
Si determina annullando la derivata seconda
y” = -18x = 0
xF = 0
Lo stesso risultato lo abbiamo, ovviamente, anche dalla formula generale, che dà:
xF = - b/3a
b è zero e quindi il punto di flesso (obliquo, dato che non annulla la derivata prima) rimane sull’asse delle y
yF = - 3· 0 + 4 · 0 + 1 = 1
La derivata seconda vale
y” = - 18 x
Il punto di flesso è F(0,1) e possiamo dire subito che per x < 0 la derivata seconda è positiva e quindi la concavità è rivolta verso l’alto, mentre per x > 0 sarà rivolta verso il basso. C’era da aspettarselo perché dalla parte negativa delle x abbiamo un minimo e dalle parte positiva un massimo. Il flesso è, perciò, discendente.
Non ci resta che calcolare la retta tangente al punto di flesso obliquo presente nell’origine.
y – 1 = m (x – 0) = mx + 1
y = mx + 1
per trovare m basta fare la derivata prima della funzione calcolata nel punto di flesso
y’ = - 9 x2 + 4
y’(0) = - 9(0)2 + 4 = 4
La retta tangente nel flesso obliquo ha equazione:
y = 4x + 1
La tangente generica aveva equazione:
y = cx + d
ed è quindi soddisfatta.
Disegniamo subito questo caso particolare nella Fig.1.
Prendiamo adesso un caso particolare, in cui si trovino soluzioni non reali che annullano la derivata prima. In poche parole, a e c devono avere lo stesso segno. Ce la caviamo abbastanza velocemente.
y = 3x3 + 4x + 1
y’ = 9x2 +4
y” = 18x
Annulliamo la derivata prima per trovare (inutilmente) i punti di massimo e minimo.
9x2 + 4 = 0
x2 = - 9/4
x = +/- (-9/4)1/2 IMPOSSIBILE
Passiamo al punto di flesso, annullando la derivata seconda:
18x = 0
xF = 0
yF = 1
La derivata seconda per valori di x < 0 è negativa e quindi la concavità è rivolta verso il basso, mentre è positiva per x > 0 e quindi la concavità è verso l’alto. Il flesso è ascendente.
Quanto vale la tangente alla funzione nel punto di flesso (0,1)?
y – 1 = m(x - 0)
y = mx + 1
m = y’(0) = 9(0)2 + 4 = 4
la tangente vale quindi
y = 4x + 1
E qui non possiamo che stupirci! Ma come, un flesso ascendente e uno discendente hanno la stessa tangente? E’ mai possibile? Non ci resta che disegnare questa funzione nella Fig. 2 e tutto risulta chiaro. Il confronto delle figure ci mostra chiaramente quanto poco conti, nei flessi obliqui, che la funzione sia crescente o decrescente. Quello che conta è che la curva attraversi la tangente arrivando da sotto (ascendente) o da sopra (discendente). Tenete presente che ho disegnato le figure in modo un po’ “rozzo”, ma potete migliorarle trovando i valori di y per vari valori di x.
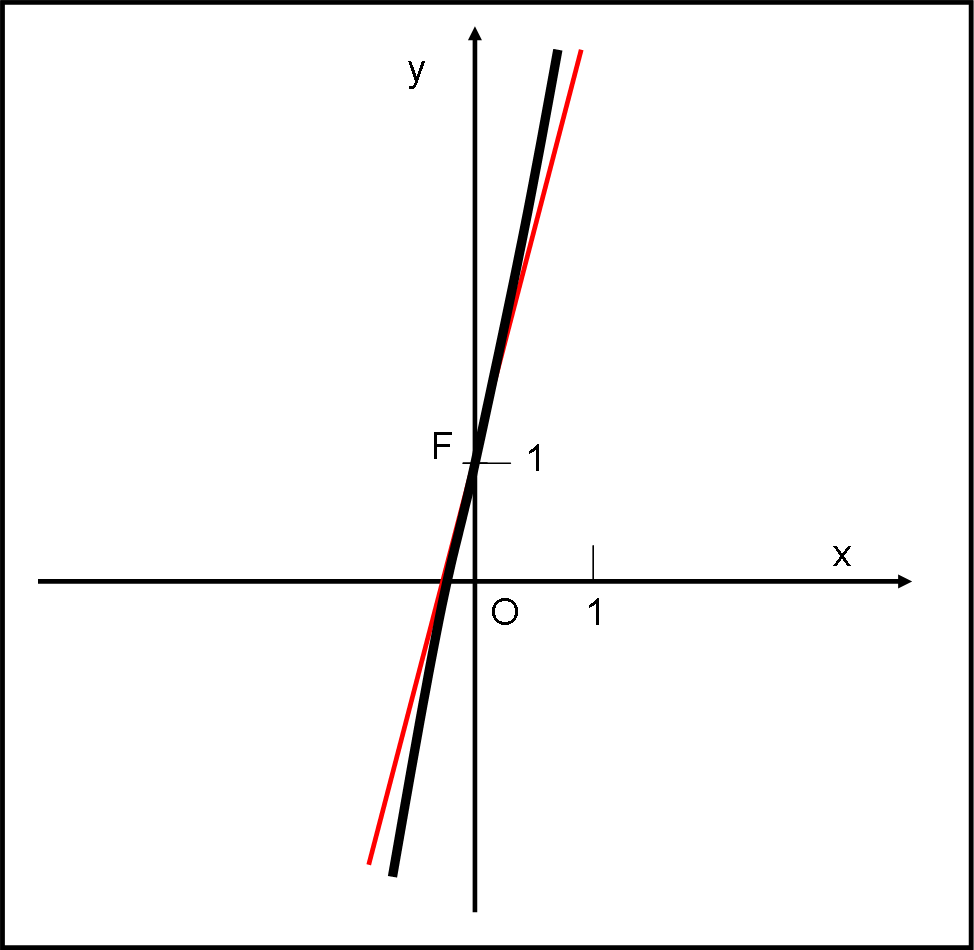
Riassumiamo quanto trovato per i flessi obliqui. Devo ammettere che anche nei libri si fa abbastanza confusione riguardo ai flessi obliqui… e a volte si preferisce escluderli. La cosa migliore è quella di studiare il segno della derivata seconda a sinistra e a destra del punto di flesso. Solo la concavità ci permette di dire con esattezza se il flesso è ascendente o discendente. Per essere ascendente la concavità a sinistra del flesso deve essere verso il basso (derivata seconda negativa) e a destra verso l’alto (derivata seconda positiva). Attenzione, però: bisogna stare abbastanza vicini al flesso per non correre il rischio di allontanarsi troppo e superare qualche massimo o minimo aggiuntivo. Questo rischio vale, ovviamente, per funzioni ben più complesse della cubica.
Quando abbiamo discusso il flesso orizzontale tutto era più facile: si vedeva proprio la funzione salire (o scendere invertendo i segni della derivata seconda). Nel flesso obliquo la faccenda non è così immediata e bisogna attentamente studiare il segno della derivata seconda e non affidarsi ad apparenze visive. Ne’, tantomeno, bisogna fare riferimento soltanto alla retta tangente. Abbiamo appena visto che con una stessa retta tangente possiamo avere sia un flesso ascendente che discendente. La rappresentazione della retta tangente, può però aiutarci graficamente guardando se la curva l’attraversa arrivando da sotto o da sopra. La faccenda, comunque, è stata già discussa quando abbiamo introdotto i flessi obliqui in generale.
Abbiamo fatto due esempi in cui manca il termine in x2. Provate da soli a fare qualche esempio in cui ci sia questo termine e manchi, invece, il termine in x (è forse ancora più facile). La prossima volta descriveremo insieme i casi della cubica completa.
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica




16 commenti
Quando che 'l cubo con le cose apprresso se agguaglia a qualche numero discreto trovan dui altri differenti in esso.
Dapoi terrai questo per consueto che 'l lor produtto sempre sia eguale al terzo cubo delle cose neto; el residuo poi suo generale delli lor laticubi ben sottratti varrà la tua cosa principale... Questi trovai et non con passi tardi nel mille cinquecente, quatro e trenta con fondamenti ben sald' e gagliardi nella città dal mar' intorno centa.
Nicolò Fontana, detto Tartaglia
(1499-1557)
Quant'è bella matematica,
che non sfugge tuttavia,
chi vuol'essern lieto sia,
del doman lei da certezza.
Lorenzo il Magnifico (quasi)
Questi lieti satiretti,
della matematica innamorati,
quindici per caverne e per boschetti
han lui posto cento agguati;
or da Bacco riscaldati....
In attesa di Enzo vi posto un'articolo tanto per http://www.media.inaf.it/2015/09/25/materia-oscura-stealth/
Accidenti, l'oscurità che crea l'oscurità!
Non vorrei che ad Enzo venisse un travaso di bile ....
...per essere precisi: fermioni oscuri confinati in nuclei oscuri da una forza oscura, equivalente oscuro dell'interazione forte... secondo me, Alvy, il Prof. non avrà un travaso di bile ma si limiterà ad una risata oscura
Una via di mezzo tra un travaso di bile ed una risata oscura

Caro Enzo ho provato a studiare approfonditamente la funzione in cui manca solo il coefficiente c (per cui cx=0).
Quindi ho provato a cambiare il segno ad ogni coefficiente, confrontando i risultati, al fine di cercare di identificare quali funzioni svolgono i vari coefficienti.
Ho deciso di separare i tre parti questo lungo post, così è possibile leggere separatamente i diversi risultati ottenuti.
Ho deciso di non utilizzare le formule generali, che rendono tutto più facile (a mio avviso i casi letterari hanno il pregio di fissare regole generali, poi ci vuole un attimo a sostituire un numero al coefficiente ed ottenere rapidamente i risultati), al fine di spiegare passaggio per passaggio il ragionamento che ho provato a fare.
Solo dopo aver svolto i vari calcoli ho costruito delle figure....
Volendo si può saltare tutto il ragionamento matematico e guardare i risultati confrontando le figure realizzate (per me sono state la prova del nove che i risultati ottenuti erano corretti).
Parto, perciò da una funzione iniziale del tipo:
y= ax³ + bx² + d …........ossia
y= 2x³ + 4x² +1 dove a=2; b=4; d=1 e c=0
Calcolo la derivata prima:
y' = 6x² +8x e l'annullo
0 = 6x² +8x
0 = x (6x +8)
la derivata si annulla:
a) se x1=0
b) se (6x +8) = 0
6x =-8
x2= -8/6 = -4/3= -1,33
Se avessi usato direttamente le formule generali letterarie, avrei ottenuto lo stesso risultato:
a) x1= 0
b) x2= -2b/3a -2(4)/3 (2) = -8/6 = -4/3
Dato che esistono due soluzioni reali in cui la derivata prima si annulla, significa che si tratta di un Minimo e un Massimo e nessun Flesso orizzontale.
Per vedere di quali punti si tratta basta vedere cosa accade alla derivata seconda:
y' = 6x² +8x
y'' = 12x +8
Sostituisco ad x l'ascissa del primo punto trovato, ossia x1=0
y'' = 12 (0) +8 = +8
La derivata seconda è positiva quindi si tratta sicuramente di un Minimo.
Sostituisco ad x l'ascissa del secondo punto trovato, ossia x2=-4/3
y'' = 12 (-4/3) +8 = -48/3 +8 = -16 +8 =-8
La derivata seconda è negativa quindi si tratta sicuramente di un Massimo.
Se avessi usato le formule generali per questo tipo di funzioni avrei ottenuto:
y1” = 2b = 2 (4) = +8 (con x1=0)
y2” = -2b = -2 (4) = -8 (con x2=-2b/3a)
Dato che conosco le ascisse di questi due punti di Minimo e Massimo, usando la funzione iniziale è facile ricavare il valore delle y corrispondenti:
y= 2x³ + 4x² +1
y1= 2 (0)³ + 4 (0) +1 = 1 (con x1=0)
Quindi il punto di Minimo ha coordinate Mi (0;1)
Per trovare l'ordinata dell'altro punto uso x2=-4/3
y2= 2 (-4/3)³ + 4 (-4/3)² +1 = 2 (-64/27) + 4 (16/9) +1 = -128/27 + 64/9 +1
y2= -128 + 192 +27/ 27 = 91/27 = 3,37 (con x2=-4/3)
Quindi il punto di Massimo ha coordinate Max (-4/3; 91/27), ossia (-1,33; 3,37)
A questo punto non resta che trovare il punto di Flesso obliquo, ossia il punto che annulla la derivata seconda.
y'' = 12x +8 annullandola si ottiene:
0 = 12x +8
12x = -8
xF = -8/12 = -2/3 = -0,66
Usando la formula generale, y= 2x³ + 4x² +1, per cui b= 4 ed a=2, si ottiene lo stesso risultato:
xF = -b/3a = - (4)/3(2) = -4/6= -2/3
Per vedere se il flesso obliquo è ascendente o discendente basta vedere il comportamento della derivata seconda:
y'' = 12x +8
dato che per valori inferiori a xF la derivata seconda è sempre negativa (concavità rivolta verso il basso), per valori maggiori di xF la derivata seconda diventa positiva (concavità verso l'alto), per esempio se x= -0,65 (che e maggiore di xF = -0,66):
y'' = 12 (-0,65) +8 = -7,8 +8 = +0,2
non può che trattarsi di un Flesso obliquo ascendente
Infatti la derivata seconda passa da valori negativi, prima del punto di Flesso, a valori positivi dopo il flesso, si tratta quindi di un Flesso obliquo ascendente.
Sostituendo nella funzione iniziale il valore di xF ricavo anche l'ordinata del punto di Flesso:
y= 2x³ + 4x² +1
yF= 2 (-2/3)³ + 4(-2/3)² +1 = 2 (-8/27) + 4 (4/9) + 1 = -16/27 + 16/9 +1 =
yF= -16 + 48 +27/27 = 59/27 = 2,185
Da notare che il Punto di Flesso si trova in mezzo ai due punti di Minimo e Massimo, non solo nelle ascisse, ma anche nelle ordinate:
Infatti
xF = -0,66 x(minimo)= 0 x (massimo) =-1,33
ma -0,66 sta proprio a metà tra le due ascisse:
(-1,33 + 0)/2 = -1,33/2 = -0,66
yF = 2,185 y (minimo)= 1 y (massimo) = 3,37
ma 2,185 sta proprio a metà tra le due ordinate:
(3,37 +1)/2 = 4,37/2 = 2,185
Quindi il punto di Flesso obliquo ha coordinate xF = -0,66 e yF = 2,185, ossia
F(-0,66; 2,185)
A questo punto rimane solo da ricavare l'equazione della retta tangente al Punto di Flesso Obliquo:
Partendo dalla relazione che contraddistingue un fascio di rette che passa per un punto, sostituisco a x0 e y0 le rispettive coordinate del punto di Flesso F(-0,66; 2,185):
y -y0 = m (x – x0)
y – (2,185) = m (x – (-0,66))
y = m (x + 0,66) + 2,185
ma m non è altro che la derivata prima della retta tangente al punto di Flesso, quindi:
m = y' = 6x² +8x sostituisco ad x l'ascissa del punto di flesso xF= -0,66
m = 6x² +8x = 6 (-0,66)² + 8 (-0,66) = 6 (0,44)+ 8 (-0,66) = 2,66 – 5,33
m = -2,66
y = m (x + 0,66) + 2,185= -2,66 (x + 0,66) + 2,185 = - 2,66x – 1,77 +2,185
y = -2,66x + 0,41
Questa è l'equazione della retta tangente il punto di flesso.
Dopo tanto calcoli, ho realizzato una figura per rappresentare la Funzione appena descritta.... non ho tracciato la curva, ma ho lasciato i punti che ho calcolato per descriverla, usando intervalli di 0,1 x, così si può vedere come la curva “rallenti” avvicinandosi ai punti di Minimo Massimo e Flesso e più in generale è possibile vedere come si comporta la curva.
http://www.astrobin.com/full/209168/I/
Paolo
PARTE 2
A questo punto vorrei capire meglio quale funzione ha ogni coefficiente, ossia voglio vedere cosa accade cambiando di segno uno o l'altro coefficiente della funzione iniziale y= 2x³ + 4x² +1.
Se cambio di segno il coefficiente a la funzione diventa:
y= -2x³ + 4x² +1
y' = -6x² + 8x che si annulla
0 = -6x² + 8x = x (-6x +
la derivata si annulla:
a) se x1=0
b) se (-6x +8) = 0
8= 6x
x2= +8/6 = +4/3 = 1,33
Per trovare i corrispondenti valori di y, basta inserire x1 o x2 nella funzione iniziale
y= -2x³ + 4x² +1
y1 = -2 (0)³ +4 (0)² +1 = 1 (con x1=0)
y2= -2 (+4/3)³ + 4 (+4/3)² +1 = -2 (64/27) + 4 (16/9) +1 = -128/27 + 64/9 +1
y2= -128 + 192 +27/ 27 = 91/27 = 3,37 (con x2= +4/3)
Per vedere di quali punti si tratta basta vedere cosa accade alla derivata seconda:
y' = -6x² + 8x
y'' = -12x +8
Con x1=0 la derivata seconda diventa:
y'' = -12 (0) +8 = +8
Quindi visto che la derivata seconda è positiva si tratta di un Minimo, esattamente come nel caso iniziale.
Con x2=1,33 la derivata seconda diventa:
y'' = -12 (1,33) +8 = -16 + 8 = -8
Quindi visto che la derivata seconda è negativa si tratta di un Massimo, esattamente come nel caso iniziale.
Ricapitolando si hanno due punti, un Minimo Mi (0; 1) ed un Massimo (1,33; 3,37)
Rispetto al risultato iniziale è cambiato il segno dell'ascissa del Massimo, ossia del secondo Punto che annulla la derivata prima (se prima il Massimo era a sinistra del Minimo ora è alla sua destra).
Ora vediamo cosa succede al Flesso obliquo, per cui annullo la derivata seconda, per trovare l'ascissa del flesso:
y'' = -12x +8
0 = -12x +8
12x = 8
xF=8/12 =+ 2/3 = +0,66
A questa ascissa corrisponde un'ordinata di.
y= -2x³ + 4x² +1.
yF= -2 (2/3)³ + 4(2/3)² +1 = -2 (8/27) + 4 (4/9) + 1 = -16/27 + 16/9 +1 =
yF= -16 + 48 +27/27 = + 59/27 = +2,185
In questo caso le coordinate del punto di Flesso cambiano solo per le ascisse, ma l'ordinata rimane uguale, F(0,66; 2,185)
Per vedere se il flesso obliquo è ascendente o discendente basta vedere il comportamento della derivata seconda:
y'' = -12x +8
dato che per valori inferiori a xF la derivata seconda è sempre positiva (concavità rivolta verso l'alto) e per valori maggiori di xF la derivata seconda diventa negativa (concavità verso il basso), per esempio se x= 0,67 (maggiore di xF=0,66):
y'' = -12 (0,67) +8 = -8,04 +8 = -0,4,
Non può che trattarsi di un Flesso Obliquo Discendente.
Rispetto al caso iniziale, se a cambia segno, il Flesso obliquo è discendente invece che ascendente, ed il punto di Flesso è spostato nelle ascisse.
Infine la retta tangente il punto di flesso dovrà avere come coefficiente angolare, il valore della derivata prima calcolato per il punto di Flesso:
m = y' = -6x² + 8x sostituisco ad x xF
m = -6(2/3)² + 8 (2/3) = -6 (4/9) +16/3 = -24/9 + 16/3 = -24 + 48/9 = + 24/9= +2,66
Il coefficiente angolare ha il medesimo valore, ma il segno è opposto.
Inserendo il coefficiente angolare m nell'equazione del fascio di rette passanti per il punto di Flesso F(0,66; 2,185):
y -y0 = m (x – x0)
y – (2,185) = m (x – 0,66)
y = m (x - 0,66) + 2,185
y = 2,66 (x - 0,66) + 2,185 = 2,66x – 1,77 + 2,185
y = 2,66x + 0,41
Rispetto a prima cambia il segno del coefficiente angolare della retta.
Come mostra la figura cambiando segno ad a è come se la curva si ribaltasse da sinistra a destra, come un'immagine speculare.
http://www.astrobin.com/full/209168/J/
Paolo
PARTE 3 = 0
= 0
A questo punto vorrei vedere cosa accade se invece di a cambio di segno b, per cui la funzione iniziale diventa:
y= 2x³ - 4x² +1
y' = 6x² -8x che si annulla
0 = 6x² -8x = x (6x -8)
la derivata si annulla:
a) se x1=0
b) se (6x -
6x = 8
x2= +8/6 = +4/3 = + 1,33
Per trovare i corrispondenti valori di y, basta inserire x1 o x2 nella funzione iniziale
y= 2x³ - 4x² +1
y1 = 2 (0)³ - 4 (0)² +1 = 1 (con x1=0)
y2= 2 (+4/3)³ - 4 (+4/3)² +1 = 2 (64/27) - 4 (16/9) +1 = 128/27 - 64/9 +1
y2= 128 - 192 +27/ 27 = - 37/27 = -1,37 (con x2= +4/3)
Per vedere di quali punti si tratta basta vedere cosa accade alla derivata seconda:
y' = 6x² -8x
y'' = 12x -8
Con x1=0 la derivata seconda diventa:
y'' = 12 (0) - 8 = -8
Quindi visto che la derivata seconda è negativa si tratta di un Massimo Max(0;1), ossia il contrario di quanto successo nei due casi precedenti.
Con x2=1,33 la derivata seconda diventa:
y'' = 12 (1,33) -8 = 16 -8 = +8
Quindi visto che la derivata seconda è positiva si tratta di un punto Minimo
Min (1,33; -1,37), ossia il contrario di quanto successo nei due casi precedenti.
Cambiando il segno di b si sono invertiti Minimi e Massimi, il Minimo con x=0 è diventato Massimo, pur mantenendo le stesse coordinate; mentre il Massimo è diventato un Minimo, sono cambiate le ordinate rispetto ad entrambi i casi precedenti, ed ora sono negative, mentre l'ascissa cambia di segno solo rispetto al caso iniziale.
Per trovare l'ascissa xF del Flesso obliquo, annullo la derivata seconda:
y'' = 12x - 8
0 = 12x - 8
12x = 8
xF=8/12 =+2/3 = +0,66
Lo stesso risultato di quando è stato cambiato segno ad a, ma il contrario rispetto alla funzione iniziale.
A questa ascissa corrisponde un'ordinata di.
y= 2x³ - 4x² +1
yF= 2 (2/3)³ - 4(2/3)² +1 = 2 (8/27) - 4 (4/9) + 1 = 16/27 - 16/9 +1 =
yF= 16 - 48 +27/27 = -5/27 = -0,185
Quindi le coordinate del punto di Flesso sono F(0,66; -0,185).
Per vedere se il flesso obliquo è ascendente o discendente basta vedere il comportamento della derivata seconda:
y'' = 12x – 8
dato che per valori inferiori a xF la derivata seconda è sempre negativa (concavità rivolta verso il basso), per valori maggiori di xF la derivata seconda diventa positiva (concavità verso l'alto), per esempio se x= 0,67 (maggiore di xF = 0,66) :
y'' = 12 (0,67) -8 = 8,04 - 8 = + 0,4
quindi, non può che trattarsi di un Flesso obliquo Ascendente
Rispetto al caso iniziale, se b cambia segno, il Flesso obliquo rimane Ascendente, ma cambiano le coordinate del Punto di Flesso, prima erano F(-0,66; 2,185) ora sono F(0,66 -0,185), dato che il flesso sta sempre in mezzo tra Minimo e Massimo la curva si è spostata sia verso destra (da -0,66 a + 0,66), sia verso il basso, tanto che Massimi e Minimi si sono invertiti.
Infine la retta tangente il punto di flesso dovrà avere come coefficiente angolare, il valore della derivata prima calcolato per il punto di Flesso:
m = y' = 6x² - 8x sostituisco ad x xF
m = 6 (2/3)² - 8 (2/3) = 6 (4/9) - 16/3 = 24/9 -16/3 = 24 - 48/9 = - 24/9= -2,66
Il coefficiente angolare è lo stesso della funzione iniziale, mentre cambiando segno ad a cambiava anche il segno di m.
Inserendo il coefficiente angolare m nell'equazione del fascio di rette passanti per il punto di Flesso F(0,66; -0,185):
y -y0 = m (x – x0)
y – (-0,185) = m (x – 0,66)
y + 0,185 = m (x – 0,66)
y = m (x - 0,66) - 0,185
y = -2,66 (x - 0,66) - 0,185 = -2,66x + 1,77 - 0,185
y = -2,66x + 1,59
Rispetto alla funzione iniziale la retta tangente il punto di Flesso pur mantenendo lo stesso coefficiente angolare, cambia il valore di n, per cui la retta si posiziona ad un'ordinata maggiore ( +1,59 rispetto a +0,41)
La figura mostra come cambiando il segno di b, la curva si è ribaltata sia da sinistra a destra, sia dall'alto al basso.
http://www.astrobin.com/full/209168/K/
Rimane solo un ultima possibilità, ossia cambiare il segno di d, ossia:
y= 2x³ + 4x² -1
Non c'è molto da dire dato che d è una costante per cui non compare in nessuna derivata (la derivata di una costante è uguale a zero).
y= 2x³ + 4x² -1
y'= 6x² + 8x.............e il nostro -1 è già scomparso
y''= 12x + 8 …...........e non può certo ricomparire dal nulla
A me sembra che l'unica funzione di d sia quella di spostare la curva verso l'alto o verso il basso.
Infatti d incide ogni volta che bisogna ricavare la coordinata y da quella x.
Prendiamo come esempio la funzione iniziale. Il punto di Minimo aveva come coordinate Mi (0;1), ossia per x1=0 si otteneva y =+1, mentre ora per x1=0, si ottiene:
y= 2x³ + 4x² -1 = 2(0)³ + 4(0)² -1 = -1
Ossia lo stesso punto Minimo ha coordinate Mi (0; -1).
Lo stesso discorso vale per il punto Massimo, le cui coordinate nella funzione iniziale erano: Max (-1,33; 3,37), per cui x2= -1,33
y= 2x³ + 4x² -1 = 2(-1,33)³ + 4(-1,33)² -1 = -4,74 + 7,111 -1= +1,37
Il Punto Massimo diventa quindi Max (-1,33; 1,37), ossia è stato spostato verso il basso di 2 unità, ossia da +3,37 a +1,37 (l'ascissa ovviamente è la stessa), dato che è variato il coefficiente d di due unità ossia da +1 a -1.
La stessa sorte capita al punto di Flesso, che prima era F(-0,66; 2,185) e che ora scommetto che la sua ordinata si abbasserà di 2 unità:
y= 2(-0,66)³ + 4(-0,66)² -1 = -0,59 + 1,777 -1 = +0,185
Infatti il punto di Flesso diventa F(-0,66; 0,185 ), e l'ordinata è passata da +2,185 a +0,185!
Il coefficiente angolare m non dipende in alcun modo da d, dato che non è altro che la derivata prima in cui d non compare:
m = y' = 6x² +8x = per cui rimane uguale, ossia m = -2,66
Cambia invece la retta finale, non certo come coefficiente angolare, ma come valore di n (mx +n.... cambia n), per cui cambia l'ordinata in cui la retta attraversa l'asse y:
y -y0 = m (x – x0)
y – (0,185) = m (x – (-0,66))
y = m (x + 0,66) + 0,185
m= -2,66
y = -2,66 (x + 0,66) + 0,185 = -2,66 x - 1,777 + 0,185 =
y = -2,66 x – 1,59
Nella funzione iniziale, invece la retta della tangente al Flesso era: y = -2,66 x + 0,41.
A questo punto a me sembra che la funzione del coefficiente d è solo quella di spostare la curva più in alto o più in basso, ossia agisce solo sulle ordinate, ma non sulle ascisse e ciò non cambia anche considerando la funzione completa con tutti i coefficienti presenti, dato che non può comparire nelle derivate.
La figura mostra chiaramente come cambiando il segno di d, semplicemente la curva iniziale si è spostata verso il basso di 2 unità.
http://www.astrobin.com/full/209168/L/
Spero di non aver detto troppe sciocchezze.... e domani vedrò di leggere il nuovo articoli sulle cubiche complete numeriche
e domani vedrò di leggere il nuovo articoli sulle cubiche complete numeriche
Paolo
Ottimo Paolo,
hai fatto un utile esercizio anche se i risultati finali potevano essere previsti sulla base dell'esponente corrispondente al singolo coefficiente. Se è quello di x, cambiando segno a x e al coefficiente tutto rimane uguale. Se è quello di x2, cambiando segno al coefficiente si cambia di segno dato che il segno di x2 rimane lo stesso... Comunque, ogni esercizio è fondamentale per prendere dimestichezza con i calcoli matematici...
@Paolo:
Complimenti per l'impegno e per la passione che ci metti.
Grazie Diego, ti dirò che trovo affascinante disegnare una curva partendo da una sequenza di numeri (una funzione)...
Paolo
caro Paolo,
anch'io l'ho sempre trovato entusiasmante! Ti fa vedere come un sacco di informazioni "reali" e "visibili" siano compresse in un piccola "frase" matematica. E' come un tema da svolgere... ti danno il titolo e tu puoi andare avanti per ore!
Complimenti ad entrambi, grazie alla frequenrtazione del blog la matematica mi sta diventando sempre più gradevole e a poco a poco comprensibile e capisco la necessità di conoscerla se si vuole capire meglio concetti astratti.


E poi qualcono diceva che l'entusiasmo è il sale della vita e a quanto pare è pure contagioso...