Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Abbiamo già dimostrato che N x N è numerabile ( nella quarta parte,l'albergo di Cantor ). Lo abbiamo fatto però in un modo un po' diverso rispetto al lavoro originale del grande matematico. Non sarei completamente soddisfatto se non lo esponessi, per dovere soprattutto storico,anche se lo giudico abbastanza complesso.

Il metodo diagonale di Cantor

Vogliamo costruire un funzione f: N x N ---> N che sia biunivoca. Nell'articolo precedente abbiamo usato il principio del minimo per ordinare i sottoinsiemi infiniti di N. Poi una volta ordinati è stato semplice metterli in corrispondenza biunivoca con N.  In N x N non abbiamo a disposizione un ordinamento, pertanto cerchiamo di crearne uno. Per contare gli elementi di un insieme, è più facile metterli in ordine. Pensate a quanto sia facile contare le tacche di separazione dei binari della ferrovia, rispetto a quanto sia difficile contare un gruppo di bambini che si muovono in continuazione; se in qualche modo non riusciamo a raggrupparli in delle file, risulta quasi impossibile. Consideriamo le coppie (x,y) che hanno una somma costante uguale ad un certo numero naturale n, cioè x+y=n

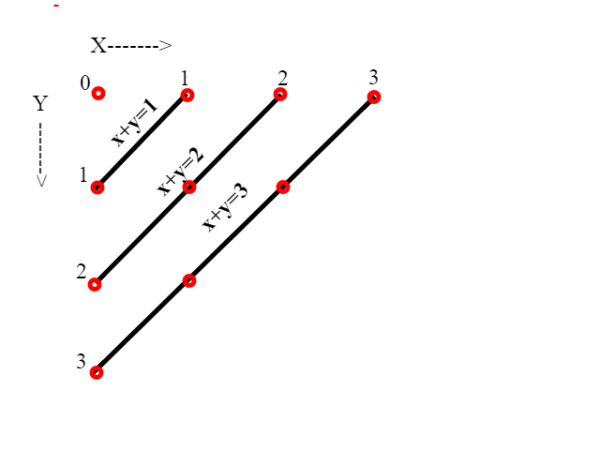
Se n=0 ho solo la coppia (0,0)

Se n=1 ho le due coppie (0,1) e (1,0)

Se n=2 ho tre coppie (0,2),(1,1),(2,0)

Facendo scorrere n da 0 a infinito copro tutte le coppie di N x N; notiamo poi che all'interno del gruppo con x+y=n, metto prima le coppie con x più piccolo. Così facendo sono anche riuscito ad ordinare le coppie.

Per ogni n ho dei gruppi (x,y) con somma uguale a n.

Come creare una corrispondenza biunivoca con N?  Semplicemente contando questi punti. Ricordiamo che contare stabilisce un applicazione biunivoca fra un insieme e N.

Per n=0 (0,0) ne ho solo uno e lo associo a 1.

per n=1  ne ho due  (0,1)  (1,0)

 per n=2 (0,2) (1,0) (2,0)  (n=2) ne ho tre

Per n=3  (0,3) (1,2),(2,1) (3,0)  ne ho quattro.

(notiamo che per ogni n ho n+1 punti (x,y) con somma uguale ad n)

quindi fino alla diagonale n=3 ne ho contati  1+2+3 +4=10. In pratica scorriamo diagonale per diagonale (le diagonali considerate sono quelle nere)  ; se esauriamo completamente le diagonali fino a n, ho 1+2+3+4+...n punti; Ma questa formula altro non è che la somma dei primi n numeri interi; abbiamo visto in vari modi che tale somma è n(n+1)/2.

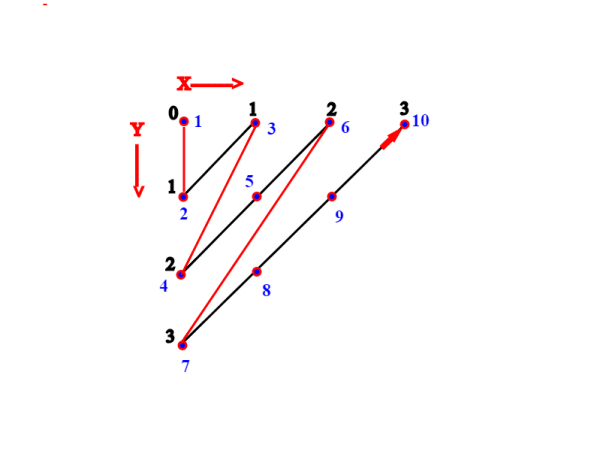
Questo è valido se esaurisco completamente la diagonale , corrispondente ad un certo n. Ma se (x,y) sono generici e voglio avere il valore della funzione, ovvero del conteggio ?

Consideriamo il caso n=3

Ho le coppie: (0,3) (1,2),(2,1) (3,0) con x+y=3 e 0<=x<=3. Supponiamo di voler vedere dove va la coppia (1,2). Considero la diagonale precedente che ho esaurito, quindi sono arrivato a contare fino a 1+2+3=4*3/2=6. Quindi devo sommare 2 per arrivare a (1,2), che occupa la seconda posizione. Quindi (1,2)-->8. Dati (x,y) qualsiasi (ma con il vincolo che la somma sia un certo n), sappiamo dunque che x+y=n per un certo n; ma allora per ottenere i valori successivi prima contiamo i precedenti 1+2+3+...n=n(n+1) /2, poi facciamo variare la x da 0<=x<=n; tenendo conto che n=x+y e n+1=x+y+1

1+2+3+....n=n(n+1)/2=(x+y)(x+y+1)/2

Per contare i punti successivi basta sommare a questa somma x +1  (naturalmente con  0<=x<=n).

Arriviamo allora a scrivere la formula, valida per qualsiasi x,y:

(x,y)---> (x+y) (x+y+1)/2 +x +1

Per come è costruita, la funzione è crescente, parte da 1 e incrementa di 1 ad ogni passo quindi è biunivoca fra N x N -->N+ (copre tutti i numeri naturali maggiori di 0). Ma N+ è anch'esso numerabile (basti pensare all'albero di Hilbert, o al fatto che è un sottoinsieme infinito di un insieme numerabile, quindi è numerabile), quindi N x N è numerabile.

 

Osservazioni su interi e razionali.

Disporre i numeri interi e i razionali sulla retta.

 

 

 

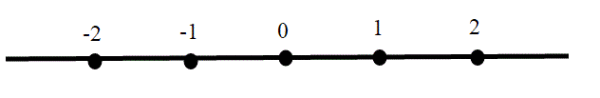
Possiamo disporre i numeri interi su una retta fissando una origine O e stabilendo una unità di misura (un segmento unitario, ad esempio 1 cm), e un verso, che andrà da sinistra verso destra.I punti corrispondenti ai numeri staranno a destra  o sinistra di O a seconda che siano positivi o negativi, e la loro distanza dall'origine sarà un multiplo fra il numero e l'unità di misura fissata. Otteniamo in questo modo una corrispondenza fra i numeri interi e i punti della retta. Per ogni numero intero ne esiste un altro che immediatamente lo precede nella successione ordinata dei numeri interi ed un altro che immediatamente lo segue. Notiamo però  per esempio, che  tra 0 e 2 (in Z) esiste il numero 1, ma tra 0 e 1 non troviamo alcun numero intero.

L'insieme dei razionali è denso.

Facciamo la stessa cosa per i razionali, per disporre un numero razionale m/n sulla retta, dobbiamo dividere l'unità di misura in n parti, e poi prendere m di queste parti, sempre partendo dall'origine , nel verso indicato dal segno del numero.

Ricordiamo che se a/b , m/n sono due razionali, diciamo che a/b<m/n se  a *n < m*b (che equivale a moltiplicare ambo i membri per b*n);

Per i razionali, osserviamo però che fra due numeri ce né sempre un terzo; infatti se a/b < m/n, basta considerare la frazione: (a+m)/(b+n) ;dimostriamo che a/b< (a+m)/(b+n)<m/n:

a/b<m/n, an<mb,  

an+ab<mb+ab (ho sommato ad ambo i membri ab)

a(b+n)<b(a+m) (raccolgo a,b a destra e sinistra

a/b<(a+m)/(b+n) ).

Lo stesso si dimostra per l'altra diseguaglianza.

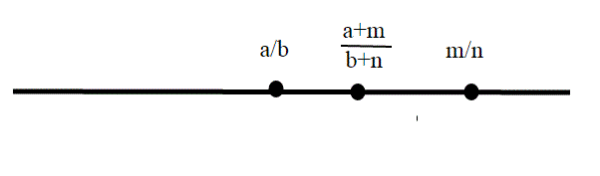
Chiaramente questo calcolo si può iterare; metto al posto di m/n (a+m)/(b+n) e riapplico la formula; trovo un punto ancora più vicino a a/b, e così via. Se all'inizio a/b=1/1000, m/n=2/1000, applicando la formula trovo un punto uguale a 3/1000; riapplicando con m/n=3/1000 trovo 4/1000 e così via.

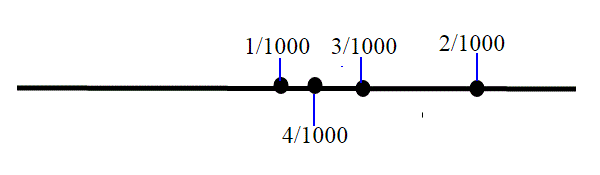
Alla fine trovo infiniti punti che si avvicinano ad a/b. Per esprimere questo fatto, diciamo che Q è denso sulla retta(anche se non copre tutti i punti sulla retta; lo abbiamo dimostrato nell'articolo sugli insiemi con l'irrazionalità di ). 

Questo fatto potrebbe far pensare che i numeri razionali siano molti di più dei relativi; invece vedremo che non è vero.Il fatto che sembrino tanti è per come sono disposti sulla retta; non riusciamo ad ordinarli come gli interi in una successione crescente, come non possiamo farlo per le coppie di numeri interi. Ma sopra  (metodo delle diagonali di Cantor) abbiamo visto come fare per aggirare l'ostacolo.

Z x Z è numerabile

Abbiamo visto nell'articolo precedente che N x N è numerabile. Ma allora anche Z x Z è numerabile, in quanto se possiamo mettere in corrispondenza biunivoca N  con Z  la stessa cosa possiamo fare con le coppie .

Infatti se sappiamo che esiste una funzione biunivoca  f: N--> Z   che a n-->z=f(n), e consideriamo una

F : N x N --> Z x Z così definita: (n,m)-->(f(n),f(m)) allora F è  biunivoca. Infatti se  la coppia  allora  almeno uno dei due elementi della prima coppia è diverso da uno dei due elementi della seconda; supponiamo sia ; essendo f iniettiva   ,  ma allora . La stessa cosa se supponiamo 

( per esempio, la coppia  pur avendo il secondo elemento uguale)

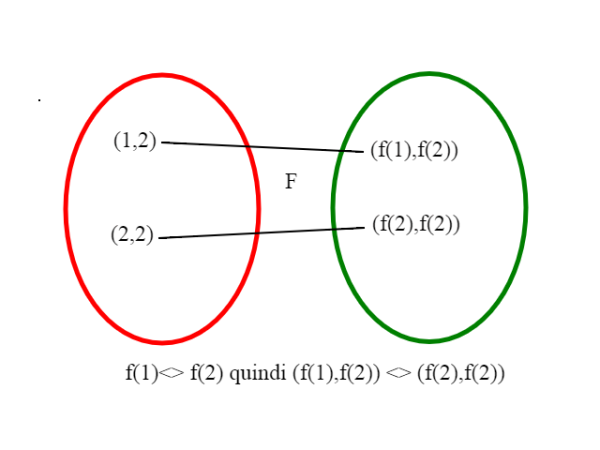
Quindi F è iniettiva.

inoltre dati (x,y) qualsiasi  in Z x Z , essendo f suriettiva  esistono n,m tali che f(n)=x, f(m)=y

quindi F è anche suriettiva.

 

L'insieme Q è numerabile

Consideriamo adesso l'insieme Q dei razionali e costruiamo una funzione in questo modo: dato un numero razionale x (una frazione ridotta ai minimi termini, con numeratore e denominatore primi fra loro) sia x=m/n.

Associamo ad x la coppia (m,n)  : otteniamo un funzione di Q-->Z  x Z

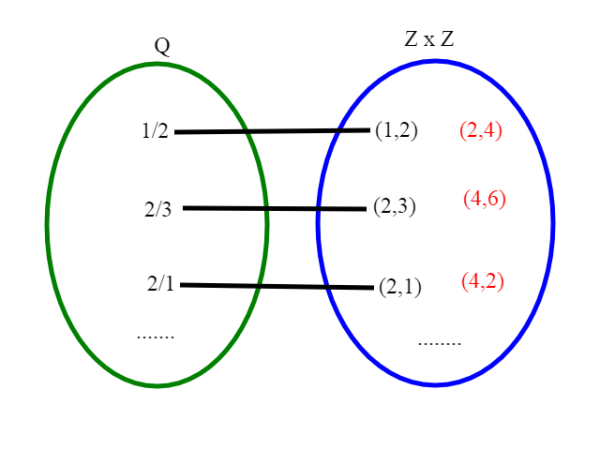
La funzione è iniettiva. Infatti se m1/n1<> m2/n2, le coppie associate sono diverse. Infatti o m1<>m2 oppure n1<>n2.

Non è però suriettiva. Per esempio:

x=1/2-->(1,2)

la coppia (2,4) di Z x Z resta scoperta ; questo perchè 2/4=1/2, ma noi abbiamo scelto una rappresentazione in cui m ed n sono primi fra loro. E così tante altre ancora, tutte le frazioni equivalenti (anche tutte le coppie (m,0 perchè non esiste un x razionale con denominatore uguale a zero).

Chiaramente non copriamo tutto Z x Z, ma abbiamo solo una corrispondenza biunivoca fra Q e un sottoinsieme (infinito) di Z x Z .

Questo però non deve preoccuparci affatto;per quanto visto nell'articolo precedente (che trovate QUI) un sottoinsieme di un insieme infinito è numerabile. Quindi Q è numerabile.

 

Cantor, parte sesta:Il minimo ordine di infinito

Cantor pare quinta,Il principio di induzione

Cantor, parte quarta. L'abergo di Cantor

CANTOR parte Terza, gli insiemi numerabili

CANTOR parte Seconda: Corrispondenze e funzioni

CANTOR parte prima, gli insiemi

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica