Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nell'articolo sugli insiemi abbiamo visto chi è l'insieme prodotto di due insiemi A e B.

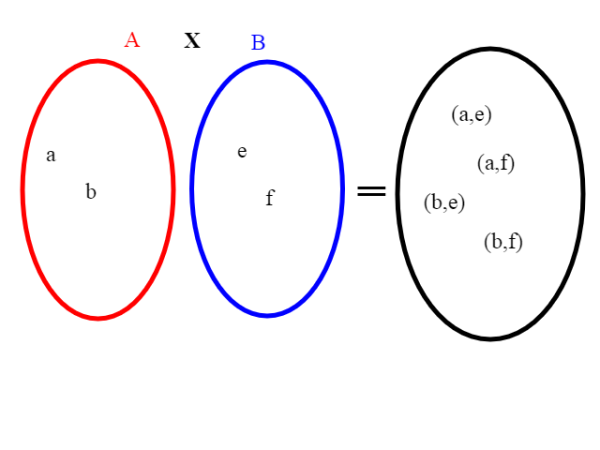
Abbiamo definito l' insieme prodotto di A con B (e lo indichiamo con A x B) l'insieme delle coppie che si ottengono prendendo un elemento da A e uno da B in tutti i modi possibili. Se A e B sono A=(a,b,) e B=(e,f), l'insieme prodotto è costituito dai seguenti elementi:

A X B = ((a,e),(a,f),(b,e),(b,f)). Notiamo che se A ha n elementi e B m elementi l'insieme prodotto ha n *m elementi.

Quindi nel caso di insiemi finiti l'insieme prodotto è più numeroso dei singoli insiemi.Ma nel caso di insiemi infiniti? Vogliamo analizzare la cardinalità dell'insieme N x N, ove N è l'insieme dei numeri naturali.

 

L'Albergo di Hilbert (N)

Riprendiamo un esempio che avevamo espresso nell'articolo precedente.

L'albergo di Hilbert  ha infinite stanze che sono numerate come i numeri naturali(0,1,2,3,...). Le camere occupabili  sono tante e quante i numeri naturali.

L'albergo di Cantor (N x N)

L'albergo di Cantor è molto più grande dell'albergo di Hilbert ; oltre ad avere infinite camere ha anche infiniti piani.

 

	0	1	2	3.
0	(0,0)	(1,0)	(2,0)	(3,0)
1	(0,1)	(1,1)	(1,2)	(1,2)
2	(0,2)	(1,2)	(2,2)	(2,3)

La  camera (1, 2) sarà la camera 1 del piano 2.  Se n, m sono numeri naturali la camera (n,m) sarà la camera n del piano m.

A causa di un principio di incendio, l'albergo di Cantor deve essere evacuato. Si pensa di traferire i clienti nell'albergo di Hilbert.

(Se camere e piani fossero in numero finito, il problema  avrebbe soluzione solo se il prodotto piani x camere dell'albergo di Cantor fosse minore o uguale al numero di camere dell'albergo di Hilbert.)

Ma come è possibile? Le stanze dell'albergo di Cantor  sembrano molte di più di quelle dell'albergo di Hilbert. L'albergatore, che è lontano parente di Cantor, lo chiama  e gli chiede come può fare. Cantor gli dice di trasferire ordinatamente i clienti procedendo per piano, senza mandare tutti i clienti del piano zero dell'albergo di Cantor direttamente nell'albergo di Hilbert, altrimenti lo occuperebbero tutto .  Gli dice: manda i clienti del piano zero ad occupare una camera si e una non dell'albergo di Hilbert. In pratica il piano zero va ad occupare  le camere pari dell'albergo di Hilbert.

Passiamo al piano 1 dell'albergo di Cantor. Ho a disposizione tutti i numeri dispari,  ma occupo lo stesso una camera si e una no, per lasciare spazio ai clienti del piano 2:

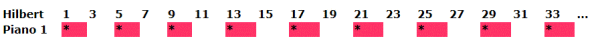
e così via ; lascio sempre libera una camera si e una no:

In questo modo ogni cliente trova prima o poi la sua camera corrispondente .
Da questo segue che l’albergo di Cantor ha lo stesso numero di camere di quello di Hilbert. Ma l'albergo di Cantor non è altro che N x N (insieme prodotto di N). Quindi N x N è numeroso quanto N.

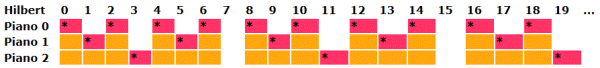
Ma i clienti sono un po' spaventati, c'è rischio che si comportino in modo non ordinato, andando ad occupare le camere in modo casuale.

Allora l'albergatore chiama di nuovo Cantor, e gli chiede: come posso dire al cliente della camera (x,y) , ad esempio camera 3 del piano 2, che camera andrà ad occupare nell'albergo di Hilbert? Cantor gli risponde: digli che vada ad occupare la camera   

partiamo dal piano 0. la formula diventa  che sono proprio i numeri pari.

Piano 1:              

dando ad x i valori 0,1,2,3,4,5.. ottengo la successione 1,5,9,13,17,21,25..

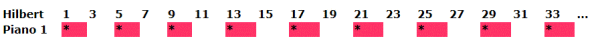
Piano 2:                                        

dando ad x i valori 0,1,2,3,4,5.. ottengo la successione 3,11,19,27,35,43,..

Grazie a questa formula possiamo dare una dimostrazione rigorosa del fatto che  N x N è numerabile.

La funzione f: N x N -->N  (x,y)--->  è biunivoca.

Possiamo limitarci a studiare la funzione  (il -1 serve solo per far saltar fuori lo 0 con x=0, y=0)

La funzione f è suriettiva.

Partiamo dall'osservazione che ogni numero naturale positivo può essere dato dal prodotto di una potenza di 2 con un numero dispari. Infatti un numero o è pari o è dispari; se è pari possiamo senz'altro esprimerlo per una potenza di 2 moltiplicata per un numero dispari ; se è dispari (n=2x+1), ricordando che  ,  moltiplichiamo  il numero stesso e per 1.

La funzione f è iniettiva.

si vede poi  subito  che coppie diverse (x,y) danno valori diversi, quindi è iniettiva;

Quindi essendo iniettiva e suriettiva allora è una corrispondenza biunivoca fra N x N e N

Quindi anche N x N è numerabile.

Articoli precedenti:

CANTOR parte Terza, gli insiemi numerabili

CANTOR parte Seconda: Corrispondenze e funzioni

CANTOR parte prima, gli insiemi

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica