Questo articolo cosituisce un "intermezzo" necessario a fornire strumenti utili per la prosecuzione dello studio degli infiniti di Cantor
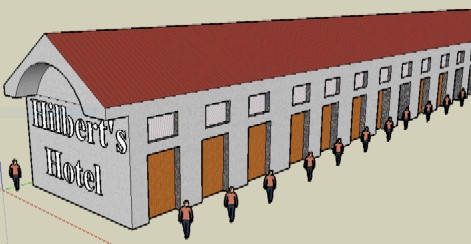
Se le infinite stanze dell'hotel "Hilbert" non sono sufficienti, ci si può trasferire da Cantor...
Affermiamo intanto che un insieme è finito se riusciamo a contare il numero dei suoi elementi. Tale numero è proprio la cardinalità dell'insieme.
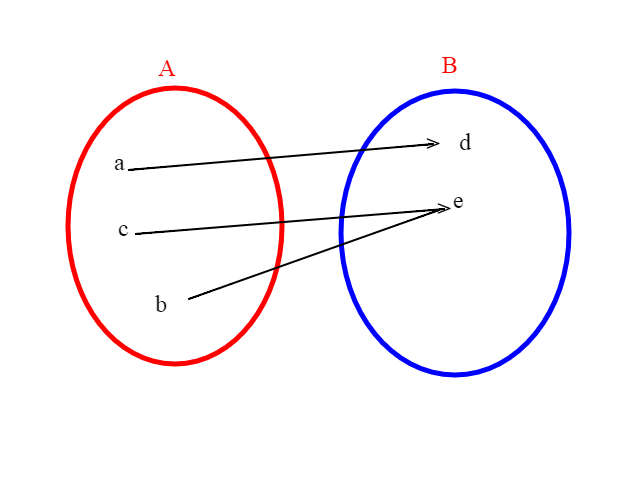
Adesso che abbiamo introdotto il concetto di insieme, vediamo come legare fra loro due insiemi.
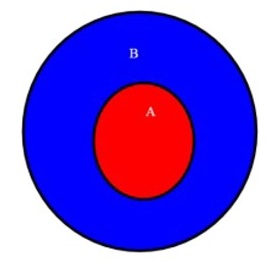
Già nell'antica Grecia era noto il concetto di infinito, Galileo aveva già compreso a quali paradossi può portare, ma la formulazione matematica rigorosa è dei tempi moderni (circa nel 1878) ed è dovuta a Georg Cantor. Il grande matematico David Hilbert disse di lui: « Nessuno riuscirà a cacciarci dal Paradiso che Cantor ha creato per noi. »
Un premio Nobel più che giusto quello di Giorgio Parisi e fa un po' ridere che non molto tempo fa un virologo o immunologo o infettivologo, fate un po' voi, che è sempre presente in TV, lo abbia accusato, in modo più o meno trasparente, di non sapere leggere e interpretare i dati. Penso che oggi tale illustre personaggio televisivo avrebbe voluto mordersi la lingua, anche perché proprio i dati sono fondamentali per gli studi eseguiti da Parisi e che gli hanno valso il Nobel.
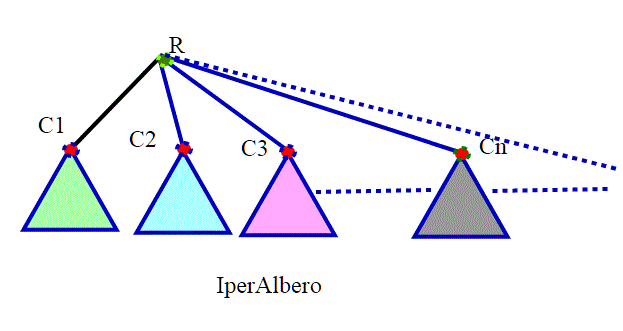
Questa miniserie avrà un seguito, che sarà proprio la "soluzione" del paradosso. Non è un quiz, ma mi piacerebbe molto se qualcuno avesse qualcosa da dire a riguardo, sfruttando soprattutto gli articoli citati alla fine del presente articolo.
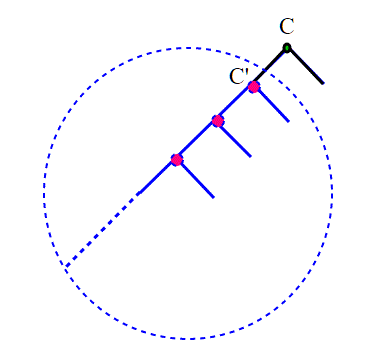
Ormai stiamo spaziando da un argomento all'altro della matematica, anche con piccoli concetti che, pur essendo intuitivi, forse non hanno mai avuto nella nostra esperienza matematica una precisa collocazione. Chiariamo bene prima il concetto di albero, per affrontare poi un simpatico paradosso che può essere denominato come la versione geometrica dell ultra famoso paradosso di […]
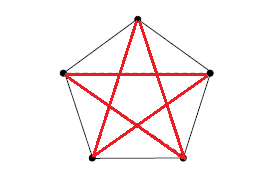
Continuiamo con questi mini-articoli non troppo impegnativi ma che servono anche per distrarci un pò. Proseguiamo verso le teorie di Ramsey con piccoli passi. Passeremo anche attraverso un altro quiz. La matematica discreta è un pò come la teoria degli insiemi; è astratta ma è semplice e affascinante, ed inoltre non richiede prerequisiti matematici profondi […]
Vorrei cambiare un po' metodo di stesura degli articoli, e farne tanti di piccole dimensioni , su cose semplici, ma che magari sfuggono alla conoscenza della maggior parte dei lettori. Non mi sono dimenticato della serie su Poincarè, ma l'articolo che sto preparando sulla connessione fra metrica e curvatura è impegnativo, e richiede molto tempo. Introduco questo […]
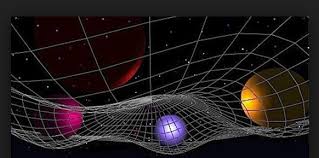
Un articolo un po' più tecnico dei precedenti, che purtroppo presuppone la conoscenza delle derivate. Tuttavia ciò ci permetterà di sfatare definizioni e formalismi tipici della geometria differenziale, quali i tensori metrici e gli elementi di linea infinitesimi. Ricordiamoci che il nostro scopo è quello di capire come vivere all'interno di una varietà dove di euclideo resta ben poco. In ogni caso, però, tramite il piano tangente possiamo ridurci sempre ad esso.
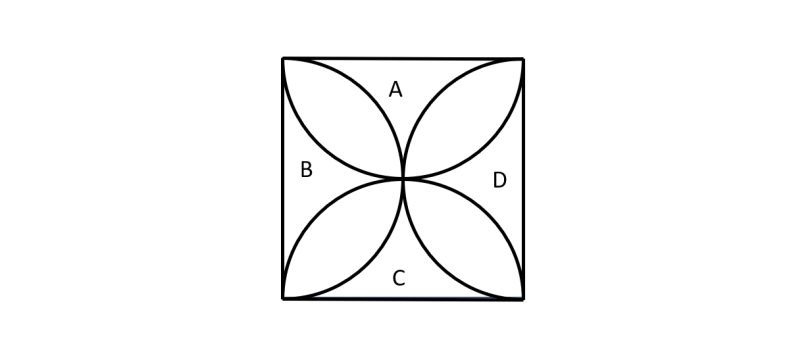
Un semplice problema geometrico ci dà l'occasione di utilizzare un metodo apparentemente più lungo e faticoso, ma di grande interesse per casi molto più complicati. Sconfiniamo nella teoria degli insiemi, ma in modo decisamente elementare.
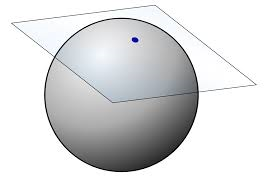
Se vogliamo addentrarci correttamente alla comprensione delle varietà Riemmane, abbiamo bisogno di qualche concetto riguardante argomenti di matematica avanzata, che di solito di studiano nei primi due anni di università . Chiaramente non è nei nostri scopi né nelle nostre possibilità approfondire tali argomenti. Provo perciò a presentarli in modo pratico-intuitivo, sfruttando anche il lavoro fatto da Vincenzo e da Fabrizio. Parleremo di matrici e del loro prodotto, di derivate parziali e equazioni parametriche, nonché di prodotti scalari. Spero che questo sia sufficiente per comprendere uno dei concetti più belli e potenti della matematica che è alla base delle teorie relativistiche e della cosmologia: le varietà Riemmane.
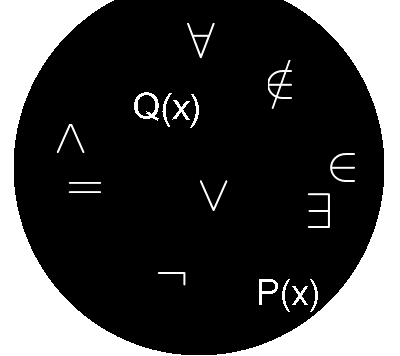
Questo articolo è la continuazione della miniserie riguardante i paradossi insiemistici, che trovate nell'archivio di matematica. Nel primo articolo abbiamo visto come la costruzione assiomatica di Zermelo-Fraenkel permette di eliminare il paradosso di Russel, e anche quello dell'insieme universale (esistenza dell'insieme di tutte le cose). Lascia però degli interrogativi; se l' "insieme" di Russel e l' "insieme universale" non sono insiemi, allora cosa sono?
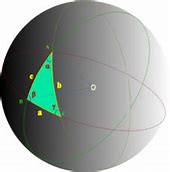
Purtroppo la congettura di Poincarè non è risolvibile con gli strumenti topologici, che sono qualitativi. Abbiamo bisogno di strumenti quantitativi, per risolvere tale congettura. Perciò introduciamo in questo articolo e nel prossimo un breve riassunto sui concetti più importanti della geometria differenziale; le varietà differenziali e quelle dotate di metrica.
Nella serie "MATEMATIZZIAMO IL NASTRO DI MÖBIUS", abbiamo visto come generare delle varietà bidimensionali in modo astratto. Riprendiamo in modo meno formale tale procedimento,estendendolo allo studio delle tri-varietà,ossia le varietà di dimensione tre,che non sono rappresentabili nello spazio tridimensionale.