I grafi completi **
Continuiamo con questi mini-articoli non troppo impegnativi ma che servono anche per distrarci un pò. Proseguiamo verso le teorie di Ramsey con piccoli passi. Passeremo anche attraverso un altro quiz. La matematica discreta è un pò come la teoria degli insiemi; è astratta ma è semplice e affascinante, ed inoltre non richiede prerequisiti matematici profondi di nessun tipo.
Prima di parlare di grafo completo dobbiamo parlare prima di grafo; abbiamo cominciato a farlo qui, dove abbiamo parlato di grafi e di sentieri euleriani. Riprendo un pò quanto scritto in quell'articolo, sulla definizione di grafo.
Cos'è un grafo?
Non daremo certo una definizione formale.
Un grafo, è proprio quello che ci propone intuitivamente la parola "grafo"; un grafo serve per tradurre in ambiente grafico determinati problemi matematici.
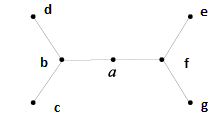
Una rappresentazione di questo tipo prende il nome di grafo. .
I punti a,b,c,d,e,f,g si chiamano vertici o nodi; gli archi che li uniscono sono gli spigoli o lati del grafo. Il grado di un nodo è invece il numero di lati che convergono in un nodo. Notiamo una cosa importante; possiamo percorrere il lato di un nodo in entrambi le direzioni, ossia sia entrando nel nodo che uscendone. Una cosa molto importante in un grafo è la connessione: un grafo è connesso se comunque siano scelti due nodi, esiste un percorso che li unisca. Ci occuperemo principalmente di grafi connessi.
Diremo che un grafo è completo se ogni vertice è collegato a tutti i vertici rimanenti.
Nella figura seguente potete vedere vari esempi di grafi completi.
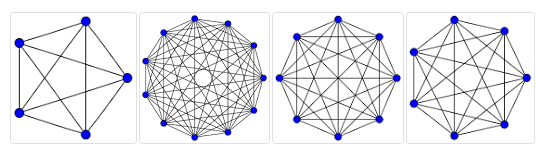
In un grafo completo su n vertici, il numero degli archi è di conseguenza uguale al numero di sottoinsiemi con due elementi dell'insieme dei vertici, quindi ; tale numero è infatti uguale al numero delle combinazioni semplici. I lati sono tanti quanti le possibili coppie di vertici scelti a caso, e senza contare dell'ordine in qui vengono considerati, in quanto restano associati allo stesso lato. Se non ve lo ricordate, un pò di calcolo combinatorio lo abbiamo visto qui.
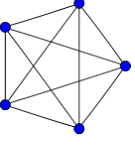
Nella figura seguente potete verificare che i vertici sono 5 e i lati 10; infatti 5*4/2=10
Tanto per formalizzare un po' le cose, chiamiamo un grafo completo con n vertici. Chiamiamo adesso colorazione di un grafo una qualsiasi assegnazione di colori, presi da un certo insieme, ai lati dei grafo che chiamiamo G. Dato un grafo G a cui sia stata assegnata una tale colorazione, diremo che un sottografo di G è monocromatico se, nella colorazione data, i suoi lati hanno tutti lo stesso colore (cosa sia un sottografo di G è abbastanza intuitivo; basta prendere il grafo completo composto da un sottoinsieme di vertici di G).Il problema che ci proponiamo adesso, e che si collega alle teorie di Ramsey, è il seguente: in
esiste sempre, qualsiasi sia la colorazione, un triangolo monocromatico, ovvero un sottografo con tre vertici? La risposta è no basta guardare la figura seguente:
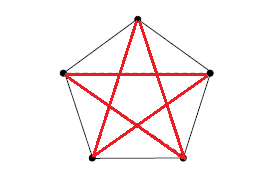
Ci basta infatti solo un controesempio: questa colorazione rosso-nera non contiene nessun triangolo monocromatico. Vi faccio notare che la colorazione è la cosa più semplice che possiamo usare nel caso dei grafi; ma nei problemi reali può essere una qualsiasi altra relazione fra coppie di oggetti.
Bene, abbiamo fatto un altro passo avanti. La prossima volta vi occuperete di .





