Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Vi ripresento sotto mentite spoglie un problema famoso come " Problema dei Ponti di Konigsberg." L'ho voluto esporre in altro modo, riferendolo alla nostra magnifica città Veneta, visto che il problema non dipende nè dalla città, nè dal numero dei ponti . Il quesito infatti è un generico problema topologico, ma molto spesso viene confuso con un problema relativo proprio alla città di Konigsberg. Ma partiamo dall'inizio.

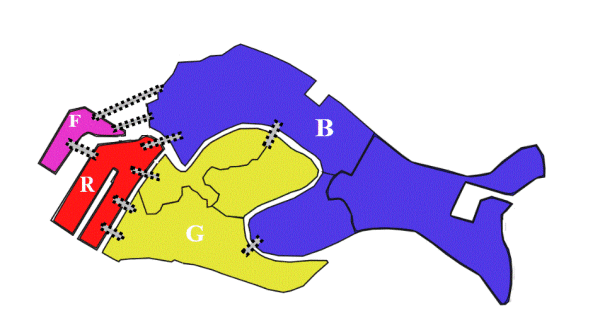Qui potete vedere una classica cartina stilizzata di Venezia( non completa) dove potete notare quattro zone di terraferma (o ridotte tali) . Le zone sono state colorate, ed è stata data ad esse una sigla (F,R,B,G) rappresentante proprio  i colori. Le divisioni all'interno delle zone con lo stesso colore rappresentano i sestieri. Tali zone di terra (o palafitta) sono collegate con dei ponti, le striscioline grige tratteggiate .Ci siamo limitati a 9 ponti, chiaramente per questioni grafiche. Venezia ha infatti 417 ponti. I ponti di Venezia non sono piani, ma vanno su e giù; una guida turistica(magari di una certa età) potrebbe porsi il seguente problema: è possibile far attraversare ai turisti di una comitiva tutti i ponti una volta solo? In fin dei conti , fare due volte un ponte già visto costituisce una fatica inutile. La guida potrebbe scegliere in ampia libertà di partire e arrivare in una zona qualsiasi.

(non è stato detto ma è implicito  che partendo da una qualsiasi delle zone  si può raggiungere una qualsiasi  delle altre con qualche ponte; si dice anche che tutte le zone sono connesse fra loro)

Di sicuro guardando la cartina , è difficile operare soluzioni; cosa posso fare? Provare tutti i percorsi possibili? Sono tanti  e non è un metodo consigliabile, in quanto risolverebbe solo questo problema con nove ponti, e non per esempio quello Ponti di Konigsberg. Mentre il discorso che stiamo per fare sarebbe valido anche per tutti i 417 ponti di Venezia.

La prima cosa da fare è semplificare il problema graficamente; In questo problema non ha alcuna importanza l'esatta posizione delle quattro regioni F,R,B,G; l'unica cosa che conta sono i collegamenti tra queste regioni, rappresentati dai nove ponti. Eliminando quindi tutte le informazioni inutili, si arriva alla seguente rappresentazione simbolica, dove i vertici rappresentano le quattro regioni e gli archi rappresentano i collegamenti tra le varie regioni costituiti dai nove ponti:

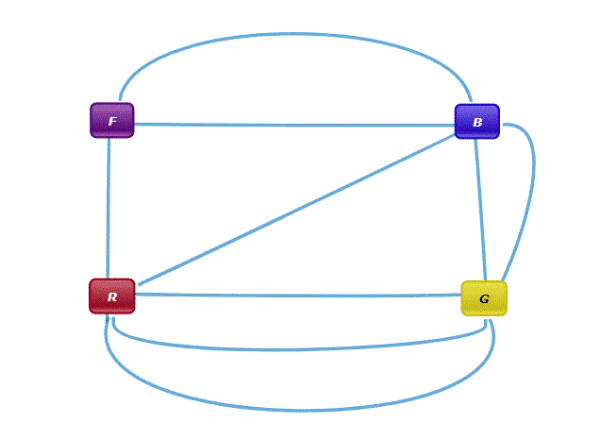
Tale rappresentazione prende il nome di grafo. Questo problema è topologico; non dipende dalle distanze , dalla estensione o dalla forma delle zone o dei ponti, ma solo dai collegamenti fra di esse. Chi ha pazienza potrebbe pensare di partire a turno da una zona, e provare tutti i percorsi  possibili, ma farebbe un lavoro per niente, perchè la guida turistica potrebbe dire; devo aggiungere altri tre ponti, o altri cinque ecc. Dobbiamo trovare un metodo che ci dica in generale se è possibile attraversare tutti i ponti una volta solo. Questo fatto  non è per niente banale; fu risolto per primo da Eulero nel 1736 prima nel caso specifico dei sette Ponti di Konigsberg, poi in modo generico. Per questo l'eventuale percorso che attraversa tutti i ponti una volta solo si chiama Sentiero Euleriano. 

La geniale  soluzione di Eulero è   sorprendentemente semplice.

Visto che siamo passati dai ponti e le zone al grafo, un po' di nomenclatura, quella strettamente necessaria.

I blocchi  F,R,B,G si chiamano vertici o nodi; gli archi che li uniscono sono gli spigoli o lati del grafo. Il grado di un nodo è invece il numero di lati che convergono in un nodo.D'ora in poi userò sempre il termine nodo, che è un alias di vertice, ma che per me è più efficace. Notare una cosa importante; possiamo percorrere il lato di un nodo in entrambi le direzioni, ossia sia entrando nel nodo che uscendone. Così come possiamo farlo per i ponti.Una cosa molto importante in un grafo è la connessione: un grafo è connesso se comunque siano scelti due nodi, esiste un percorso che li unisca. Come detto sopra il problema dei ponti di Venezia viene rappresentato con un grafo connesso. Tutto quello che diremo da qui in avanti si riferisce ad un grafo connesso.

Eulero aveva osservato che l’esistenza o meno del percorso è una proprietà del grafo, e non dipende dalla nostra capacità di trovarlo. Si può aggiungere che è  una proprietà del grado dei nodi.

Nodo di grado pari:

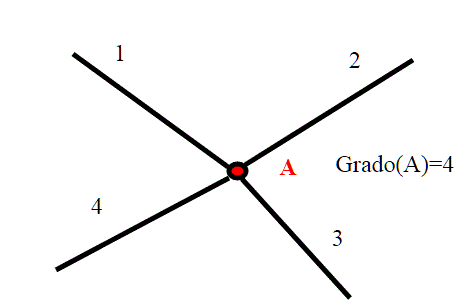
Nodo di grado dispari:

 

 

 

 

 

 

 

 

Notiamo un fatto  importante:  In un grafo la somma del numero dei gradi dei nodi è uguale al doppio del numero dei lati:

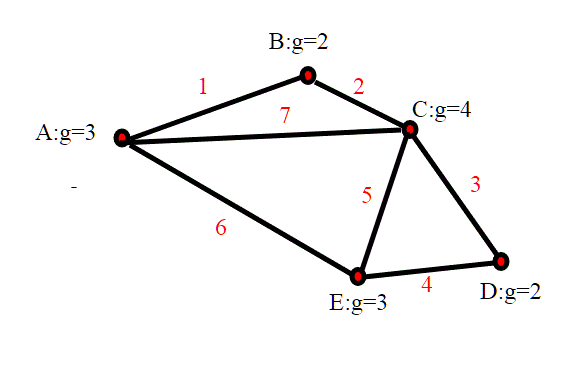
Infatti, ogni lato che unisce due nodi dà un contributo di due alla somma totale dei gradi del grafo.

Questo fatto implica un altro fatto importante: ogni grafo contiene un numero pari di nodi dispari. Infatti essendo la somma dei gradi un numero pari, ed essendo  tali gradi pari o dispari, la somma dei pari dà un numero pari, mentre la somma dei dispari dà pari solo se essi sono in numero pari. Notiamo che i nodi dispari possono essere anche zero.

 

I casi sono due: in un  sentiero Euleriano o si parte da un nodo e si arriva in un altro nodo, oppure si parte e si torna nello stesso nodo.

Il secondo caso è anche indicato come Ciclo Euleriano.

Dopo queste considerazioni preliminari, veniamo alla nostra dimostrazione. Cercheremo una condizione che senz'altro deve verificarsi se il sentiero è Euleriano. In matematica si chiama  condizione necessaria.

Distinguiamo la dimostrazione in due casi:

Caso 1:  Arrivo e partenza distinti.

Immaginiamo che esista un percorso che, partendo da un nodo di un determinato grafo, ne attraversi tutti i lati una e una sola volta. Consideriamo un nodo che non sia quello da cui si parte,nè quello in cui si arriva. Allora ogni volta che si arriva, attraverso un lato qualsiasi, in questo nodo si deve poi uscirne attraverso un lato diverso.

Quindi i lati incidenti a questo nodo possono essere suddivisi in coppie: da un lato si entra e dall'altro si esce. La conseguenza è che il numero di lati incidenti a un qualsiasi nodo diverso da quello iniziale o finale deve essere pari, ossia il nodo deve avere grado pari.

 

 

 

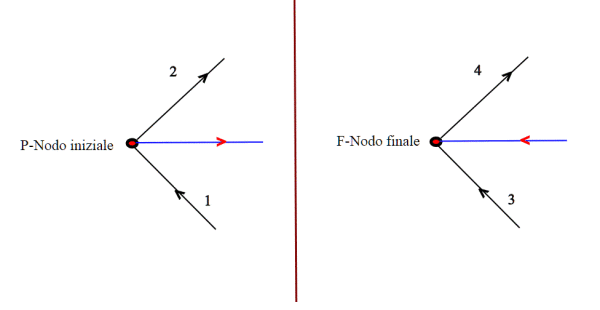
Per quanto riguarda i nodi iniziale e finale,  nel nodo iniziale c'è un lato uscente che non è accoppiato con nessun lato entrante, mentre nel nodo finale c'è un lato entrante che non è accoppiato con nessun lato uscente. Quindi, se i nodi iniziale e finale sono distinti, il numero di lati incidenti a tali nodi deve essere dispari, ovvero il nodo deve avere grado dispari. Inoltre i nodi iniziale e finale sono solo due.

Caso 2:  Arrivo e partenza nello stesso nodo.

Abbiamo visto sopra che i nodi interni, che non siano iniziali o finali, hanno grado pari; sappiamo che un grafo connesso ha un numero pari di nodi dispari. Ma allora anche il punto di partenza-arrivo deve avere grado pari. Non può essere dispari, altrimenti avremmo un numero dispari di nodi dispari.

Riassumendo: se un sentiero è Euleriano, necessariamente i nodi di grado dispari sono o  zero o due. Nel caso siano zero abbiamo un circuito Euleriano, con partenza e arrivo nello stesso nodo.

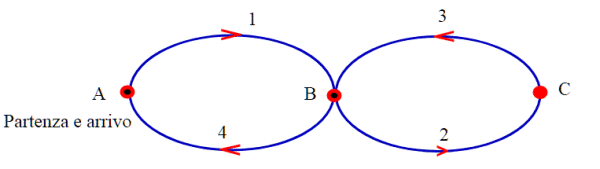
Un sentiero Eureliano con partenza e arrivo nello stesso punto A; notare che i lati  che entrano nei vari nodi sono tutti in numero pari.

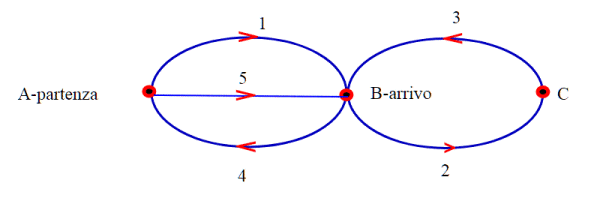
Un sentiero Eureliano con partenza e arrivo in due punti diversi; Notare che i lati che vanno in C sono pari, mentre in A e B sono dispari; altra cosa: il lato che esce da A arriva in B.

Soluzione del nostro problema dei nove ponti.

Quindi affinchè sia possibile percorre i lati una e una volta sola, il grafo deve avere o tutti vertici di grado pari, oppure al massimo due vertici di lato dispari. Torniamo al nostro  grafo dei ponti di Venezia:

il grado di F è 3,  quello di B 5, quello di R 5, quello di G 5;  abbiamo 4 nodi di grado dispari. Il problema quindi non ha soluzione (ci sono più di due nodi di grado dispari), ovvero non esiste un percorso che passi per tutti i ponti una e una sola volta. Nemmeno il Problema dei Ponti di Konigsberg ha soluzione, in quanto i vertici del grafo corrispondente hanno tutti grado dispari.

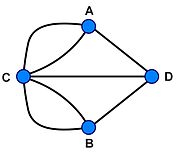
Successivamente, Eulero dimostrò che questa condizione, oltre che ad essere necessaria, è anche sufficiente.Ovvero,se in un grafo, in cui tutti i nodi siano raggiungibili, i nodi con ordine dispari sono al massimo 2, allora il grafo è un sentiero Euleriano.   Tale dimostrazione potrebbe essere il seguito di questo articolo.Concludiamo con le parole di Eulero, così come le ha scritte personalmente:

"Un qualsiasi grafo è percorribile se e solo se ha tutti i nodi di grado pari, o due di essi sono di grado dispari; per percorrere un grafo "possibile" con due nodi di grado dispari, è necessario partire da uno di essi, e si terminerà sull'altro nodo dispari."