Una soluzione... ma ne esistono sicuramente molte altre, anche non geometriche. Potete anche proporle, ma -mi raccomando- con le giuste figure e con tutti i passaggi perfettamente spiegati.


Una soluzione... ma ne esistono sicuramente molte altre, anche non geometriche. Potete anche proporle, ma -mi raccomando- con le giuste figure e con tutti i passaggi perfettamente spiegati.

Estate o non estate è ora di salire un po' di livello, visto che rispondono solo i più esperti. Prendetevi tutto il tempo necessario...
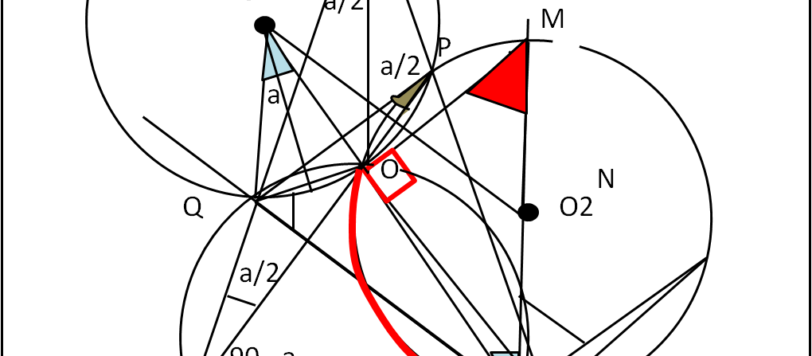
Riporto una soluzione, ma, come discusso nei commenti, ve ne sono sicuramente altre, forse più veloci...

Avevamo già trattato i solidi a n dimensioni, ma c'eravamo dimenticati di Eulero... rimediamo subito!
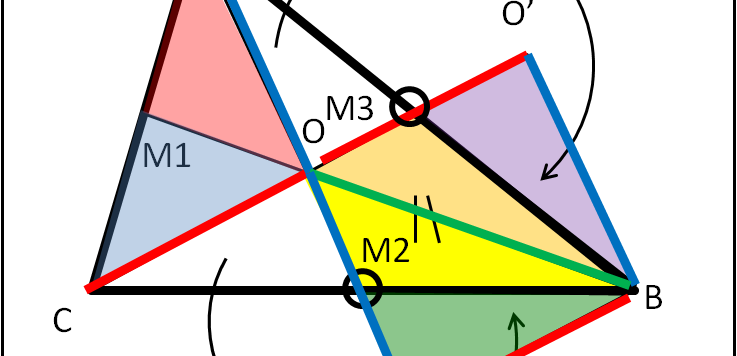
Se Pitagora ed Euclide lo sapessero si morderebbero le mani. Solo dieci anni fa è stata scoperta una proprietà delle mediane di un triangolo qualsiasi che a loro era incredibilmente sfuggita...

Uno stupefacente teorema dovuto a un matematico cecoslovacco (Karel Petr) permette di costruire un poligono regolare partendo da un poligono qualsiasi. Chi vuole divertirsi ha pane per i suoi denti...

Un quiz che serve per introdurre un paio di teoremi poco conosciuti. Sempre che non siate voi a introdurli fin dall'inizio...
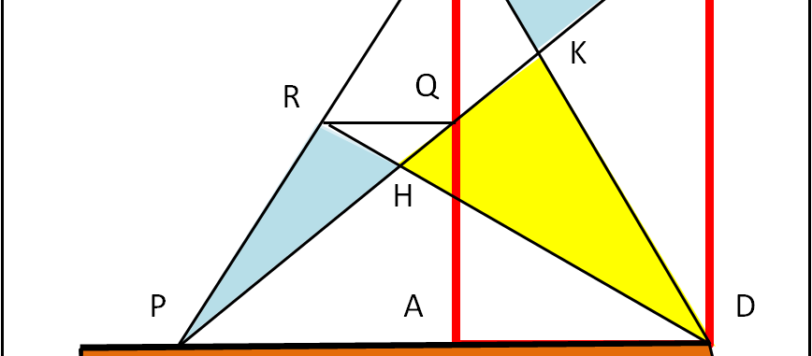
Un'avventura geometrica abbastanza curiosa che potrebbe, però, non essere lontana dalla realtà futura...

Un quiz che ho trovato piuttosto divertente, ma che ho visto essere stato dimostrato in modo un po' troppo laborioso... Tocca a voi!