Una soluzione... ma ne esistono sicuramente molte altre, anche non geometriche. Potete anche proporle, ma -mi raccomando- con le giuste figure e con tutti i passaggi perfettamente spiegati.


Una soluzione... ma ne esistono sicuramente molte altre, anche non geometriche. Potete anche proporle, ma -mi raccomando- con le giuste figure e con tutti i passaggi perfettamente spiegati.

Estate o non estate è ora di salire un po' di livello, visto che rispondono solo i più esperti. Prendetevi tutto il tempo necessario...

L'Universo segue leggi matematiche o siamo noi che abbiamo creato la matematica per descriverle ? La domanda delle domande. Accorgendoci che la spirale aurea non approssima realmente le innumerevoli spirali che ci mostra la Natura, ma che è solo una delle tante di tipo logaritmico che possiamo fare intervenire per una soddisfacente descrizione, utilizziamo la sua costruzione per valutare se un numero è irrazionale oppure no. Meglio che niente...

Avevamo già trattato i solidi a n dimensioni, ma c'eravamo dimenticati di Eulero... rimediamo subito!

Quasi quasi mi vergogno a chiedere all'IA di risolvere questi due facili problemi di matematica. Però, qualcuno di voi potrebbe anche provarci... o con l'IA o con i vecchi e trogloditici sistemi.
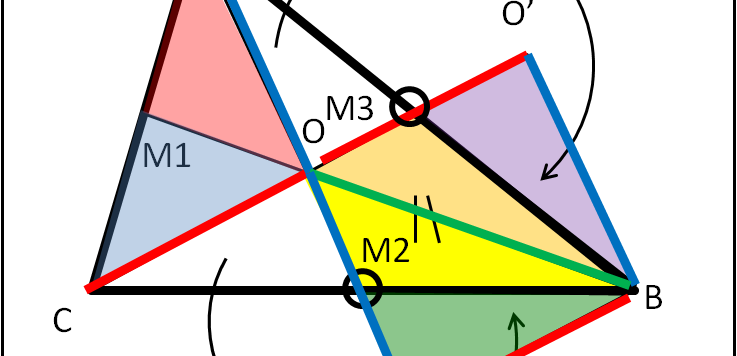
Se Pitagora ed Euclide lo sapessero si morderebbero le mani. Solo dieci anni fa è stata scoperta una proprietà delle mediane di un triangolo qualsiasi che a loro era incredibilmente sfuggita...

Uno stupefacente teorema dovuto a un matematico cecoslovacco (Karel Petr) permette di costruire un poligono regolare partendo da un poligono qualsiasi. Chi vuole divertirsi ha pane per i suoi denti...

In attesa che il prof. torni da una breve vacanza, ripeschiamo qualche "perla" che giace nascosta nei meandri dell'archivio. Questa perla l'abbiamo scelta perché ha attinenza con l'articolo sulle ruote quadrate pubblicato pochi giorni fa. Se, infatti, le ruote quadrate necessitano di strade con curvatura a forma di catenaria, le ruote di Reuleaux funzionano perfettamente anche su strade rettilinee. Scopriamo perché!
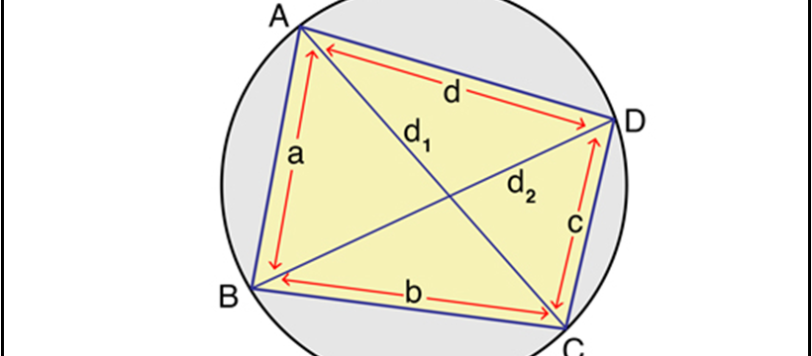
Vi è in geometria una formula non molto nota che consente di calcolare il raggio della circonferenza circoscritta ad un quadrilatero ciclico: la formula di Parameshvara, che prende il nome dal matematico e astronomo indiano Vatasseri Parameshvara Nambudiri (Kerala, India c. 1380–1460). La sua dimostrazione non è particolarmente difficoltosa in quanto si basa essenzialmente su […]

Un quiz che serve per introdurre un paio di teoremi poco conosciuti. Sempre che non siate voi a introdurli fin dall'inizio...