Il titolo vuole praticamente chiederci: "Se l'uomo non avesse inventato la ruota circolare, ma avesse usato solo ruote quadrate, come sarebbe dovuta essere la strada per muoversi nel modo migliore?"

Potrei anche essere ancora più provocatorio... Guardate la figura che segue.

Vi sembra che la strada sia perfettamente liscia o, invece, sembra composta da sassi curvi? Magari le ruote rotonde non erano le uniche a essere usate...

 

In altre parole, vogliamo dimostrare che ogni ruota ha la sua strada ideale. Iniziamo ad affrontare il problema più semplice, ossia quello della ruota quadrata.

Immaginiamo di avere le ruote quadrate e di percorrere una strada perfettamente piana. Non c'è bisogno di fare tanti calcoli per dire che le condizioni di guida sarebbero terrificanti. Una semplice constatazione ci mostra il perché. Ogni punto della ruota toccherebbe la strada, ma la distanza di questi punti dal centro di rotazione della ruota varierebbe da un minimo a un massimo. Come conseguenza il centro della ruota sarebbe costretto a salire e a scendere e quindi l'intera vettura, che è vincolata all'asse delle ruote, lo seguirebbe in questo moto non certo piacevole per il guidatore.

Ciò ci fa capire che la strada non può essere pianeggiante, ma tale che il centro della ruota percorra una traiettoria rettilinea. Questo è il requisito fondamentale che eliminerebbe qualsiasi movimento fastidioso.

Ciò che dobbiamo determinare, perciò, è l'equazione che caratterizza una traiettoria tale da mantenere il centro della ruota in moto rettilineo.

Affinché il centro della ruota (o se preferite l'asse della vettura) si muova orizzontalmente la congiungente centro e punto di contatto sul terreno deve essere perfettamente verticale. Non è difficile spiegare il perché. Immaginiamo un solido qualunque che si muova su un terreno qualunque. Chiamiamo P il punto di contatto tra solido e terreno. Il moto di rotolamento non è altro che una rotazione istantanea di tutto il solido attorno al punto di contatto. Ogni punto del solido , perciò, si muove di moto circolare attorno al punto P, ossia la direzione istantanea del suo moto è perpendicolare alla congiungente con P. Ovviamente, anche il centro della ruota descrive questo moto, ossia la sua direzione deve essere perpendicolare alla congiungente con P. Ne segue che se vogliamo che la sua traiettoria sia orizzontale, l'angolo tra essa e la congiungente con P deve essere sempre 90°, ossia deve essere verticale.

Consideriamo un qualsiasi punto del bordo della ruota. Esso si muove di moto circolare attorno al punto di contatto. Ne segue che la sua velocità attorno a tale punto varia dato che varia la distanza tra il punto al bordo della ruota e il punto di contatto. Quando il punto al bordo viene a coincidere con il punto di contatto la sua velocità deve. perciò, annullarsi. D'altra parte, se non lo facesse, il punto di contatto dovrebbe muoversi con tale velocità e, quindi, vi sarebbe un moto di scivolamento che è escluso dato che siamo in presenza di un moto di puro rotolamento.

Queste osservazioni verranno usate per caratterizzare la curvatura della strada ideale per il tipo di ruota con cui abbiamo a che fare.

Dobbiamo determinare due equazioni che descrivano la forma della ruota e della strada.

Iniziamo con la strada.

La sua forma può essere descritta nel piano x, y (asse passante per il centro della ruota e retta perpendicolare) attraverso delle equazioni parametriche del tipo

x = x(t)

y = y(t)                           .... (a)

Al variare del parametro t (che possiamo proprio considerare il tempo) ogni punto della strada deve soddisfare le due funzioni.

Passiamo alla ruota.

La soluzione migliore è quella di descriverla attraverso le coordinate polari r e θ , dove

r = r(t)

e

θ = θ(t)                               ....(b)

E' stato bello scriverle, ma bisogna anche determinare le equazioni (a) e (b) e lo facciamo sulla base delle osservazioni fatte precedentemente.

N.B.: Non confondiamo le coordinate polari di questa situazione con le solite utilizzate per la circonferenza, dove il raggio è costante ( r cos θ, r sin θ). Queste sono relative sempre agli stessi parametri  r e θ ma r è adesso una variabile.

Dalla (1) segue che il punto di contatto della ruota con il terreno deve avere sempre un valore di y negativo rispetto  al centro della ruota. Tuttavia, sappiamo anche che la y  del punto di contatto deve stare sulla verticale e, quindi, la y del punto di contatto sulla strada deve variare al variare della distanza dal centro della ruota, ossia r.  La y relativa alla strada deve perciò essere posta uguale a - r.

y(t) = - r(t)

In parole semplici, l'andamento della strada deve assecondare la variazione della distanza tra centro della ruota e punto di contatto, variabile con il tempo.

Abbiamo determinato come l'ordinata dei punti della strada si alzi e si abbassi in funzione del tempo, ma adesso dobbiamo anche determinare come vari l'ascissa dei punti della strada. Qui il ragionamento è un po' più sottile, ma cerco di semplificarlo al massimo nel modo più intuitivo possibile.

Ricordiamo  ancora una volta che il moto di puro rotolamento è descrivibile come un moto di traslazione del centro di massa O (centro del quadrato) con una certa velocità orizzontale più un moto rotatorio attorno al centro di massa con velocità angolare dθ/dt.

Al tempo t₁ Il punto O ha velocità diretta verso destra (traslazione). Il punto P si deve muovere anch’esso verso destra, essendo solidale. Tuttavia, in queste condizioni ci  sarebbe solo scivolamento.  Il punto P deve, perciò, ruotare attorno ad O con una velocità uguale e contraria a quella del punto O (Fig. 1).

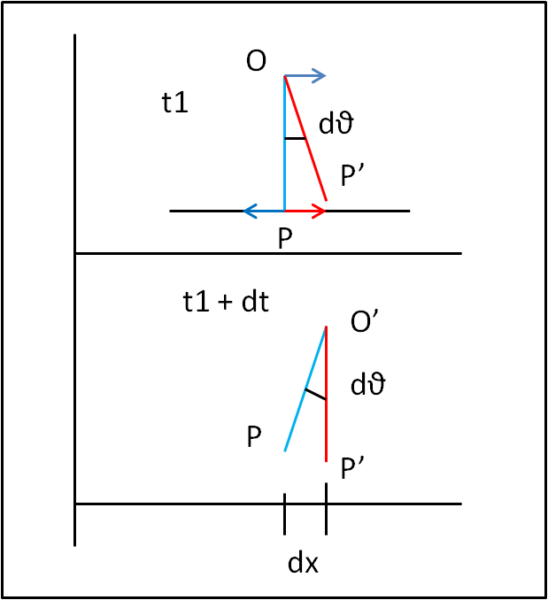
In tal modo si ha che il punto P ha istantaneamente velocità nulla. Al tempo t₂ = t₁ + dt,  O si è spostato in O’ e il nuovo punto di contatto è diventato P’ (deve essere lungo la verticale). Per ottenere lo spostamento PP’ basta moltiplicare r per dθ, dato che stiamo lavorando con variazioni infinitesime.

dx = r dθ

dx/dt = r dθ/dt

Non riusciamo, per adesso, a descrivere l'andamento dell'ascissa della strada, ma possiamo scrivere la sua "velocità", che è esprimibile come r dθ/dt. Ovviamente, l'uguaglianza vale per una variazione piccolissima dell'angolo.

Ribadiamo che r è la distanza tra centro della ruota e punto di contatto istantaneo. Notiamo che nel caso della ruota circolare questa distanza è costante e uguale al raggio, mentre nel caso del quadrato varia da un valore pari a metà del lato a un valore pari alla metà della diagonale.

Abbiamo quindi sistemato le (a), legandole alle equazioni polari della ruota

y = - r

dx/dt = r dθ/dt                                 .... (c)

Passiamo alle (b)

Dobbiamo scrivere le equazioni parametriche della ruota, ossia come variano ascissa e ordinata della ruota rispetto al suo centro in funzione del tempo t.

Per trovare queste relazioni possiamo metterci in condizioni particolari, considerando un quadrato che abbia i suoi vertici in punti semplici. La legge di rotazione non varia certo ingrandendo o diminuendo le dimensioni del quadrato.

Non solo, possiamo anche limitarci alla descrizione di un solo lato del quadrato, dato che la situazione rimane la stessa per ogni lato.

Usiamo la Fig. 2

Consideriamo il segmento verticale, per il quale la x è costante, ad esempio uguale a 1.

Chiamiamo y come parametro t. Possiamo scrivere:

x = 1

y = t

Facciamo variare t (ossia y) da - 1 a + 1 e otteniamo tutti i punti del segmento. Noi siamo interessati ad avere le coordinate polari r e θ. Piuttosto facile, ricordando che

r² = √(x² + y²)

θ = arctan (y/x)

Ossia

θ = arctan (t/1) = arctan t

r = √(1 + t²)

Queste sono le coordinate polari della ruota che devono essere introdotte nella (c) per avere le coordinate x(t) e y(t) della strada.

y = - √(1 + t²)

dθ/dt = d(arctan t)/dt = 1/(1 + t²)

dx/dt = r dθ/dt = √(1 + t²)/(1 + t²) = 1/√(1 + t²)

A questo punto dobbiamo ricordare che la derivata dell'asinh(t) vale proprio 1/√(1 + t²) *

le equazioni parametriche della strada diventano, perciò:

x = asinh t

y = -√(1 + t²)

Beh... non sono proprio immediate, sembrerebbe... E, invece, se eliminiamo il parametro t otteniamo l'equazione cartesiana della strada:

t = sinh(x)

per cui:

y = - √( 1 + sinh²(x))

y = - cosh x

Questa è una famosa curva, estremamente utile, che abbiamo già conosciuto, ossia è  una catenaria.

 

Quindi le strade rettilinee sono adatte solo a ruote circolari? Non proprio... parola di Reuleaux!