Questo articolo è inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

Cos’è una figura ad ampiezza costante? Ho avuto la fortuna di scoprirlo durante un breve stage presso la Facoltà di Matematica e sono rimasta a bocca aperta per tutta la lezione! Non immaginavo davvero che si potessero costruire biciclette con ruote che sembrano triangolari, ma che consentono di procedere come se fossero circolari, senza che il ciclista senta il minimo scossone. Non ci credete? Al termine di questo articolo avrete cambiato idea!

Andiamo per gradi, innanzitutto è necessario dare una definizione:

una FIGURA si definisce ad AMPIEZZA COSTANTE se, tracciate due tangenti alla figura stessa, tra loro parallele, facendo ruotare la figura, questa è sempre a contatto con entrambe.

La più comune figura ad ampiezza costante è il cerchio, e ciò non ci stupisce per niente, infatti:

Sembra impossibile, ma non è l’unica figura che ha questa caratteristica. Un’altra è il TRIANGOLO di REULEAUX: si disegna un triangolo equilatero, dopodiché su ogni lato, puntando il compasso in ogni vertice, si costruisce un arco di cerchio con raggio uguale alla lunghezza del lato.

 

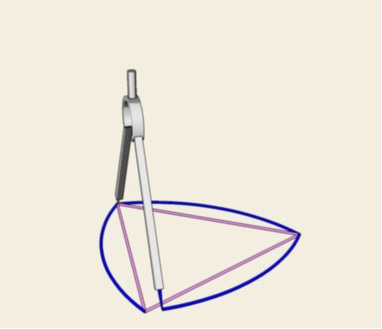
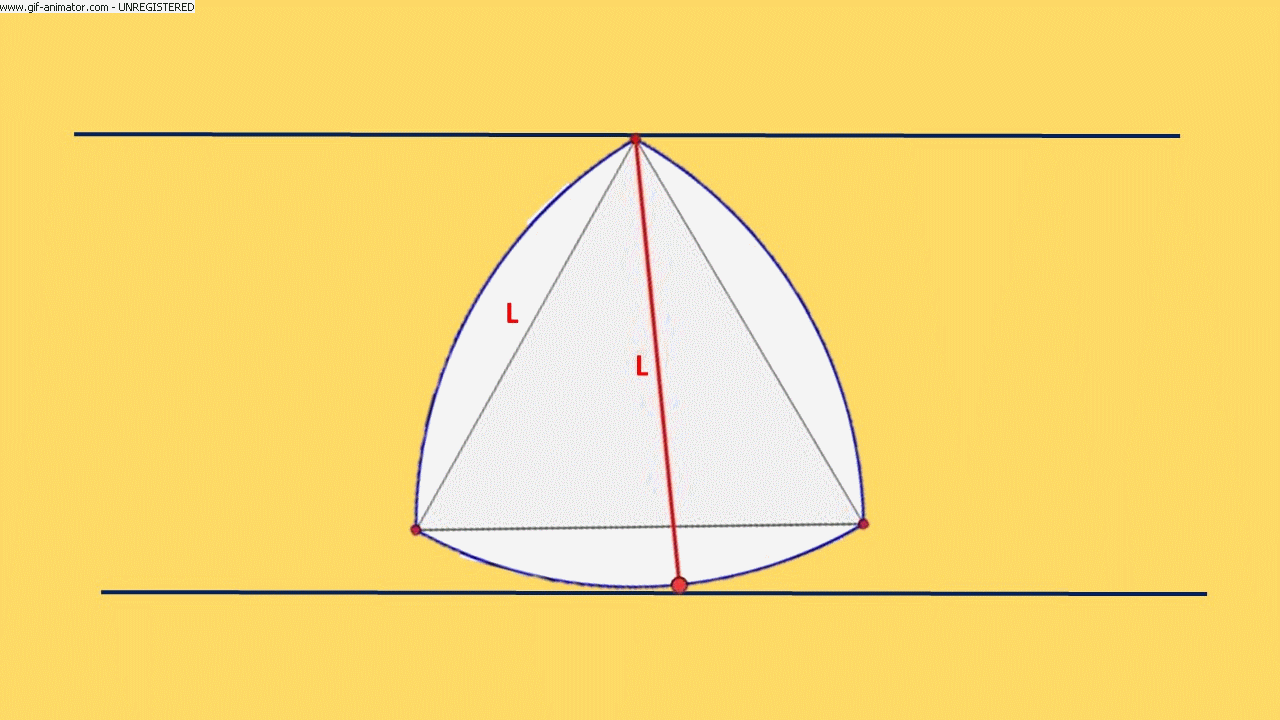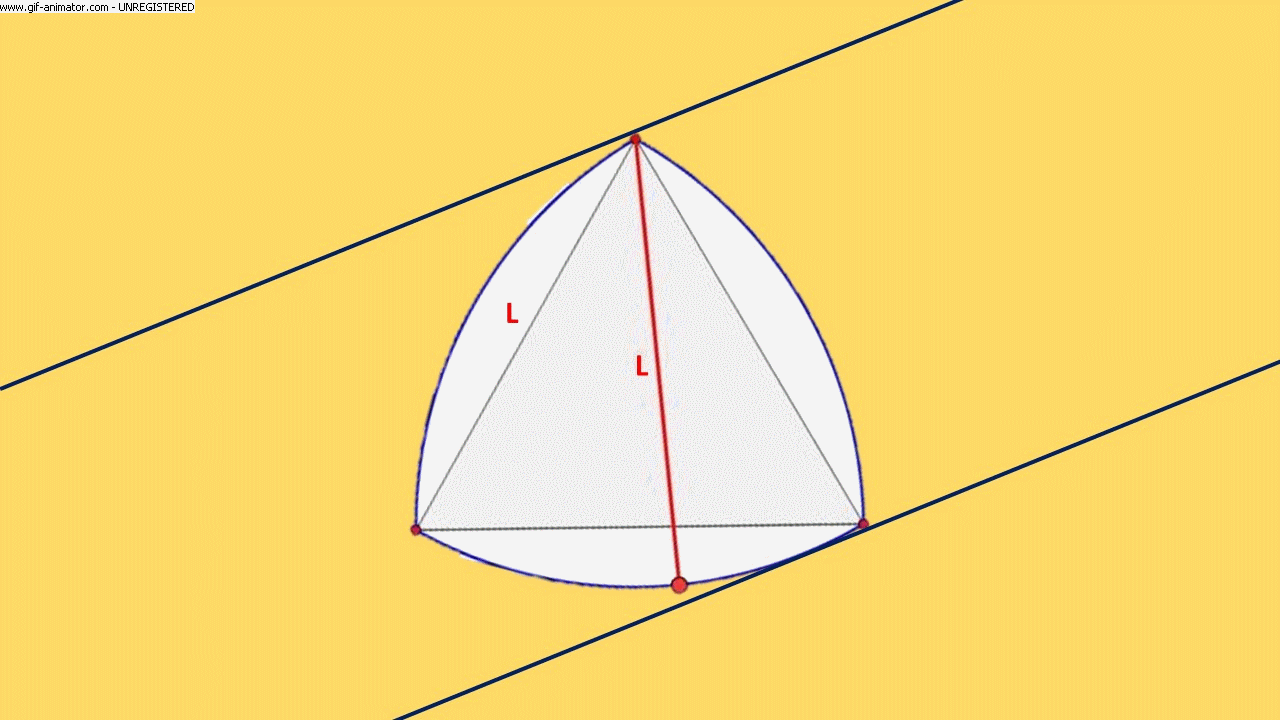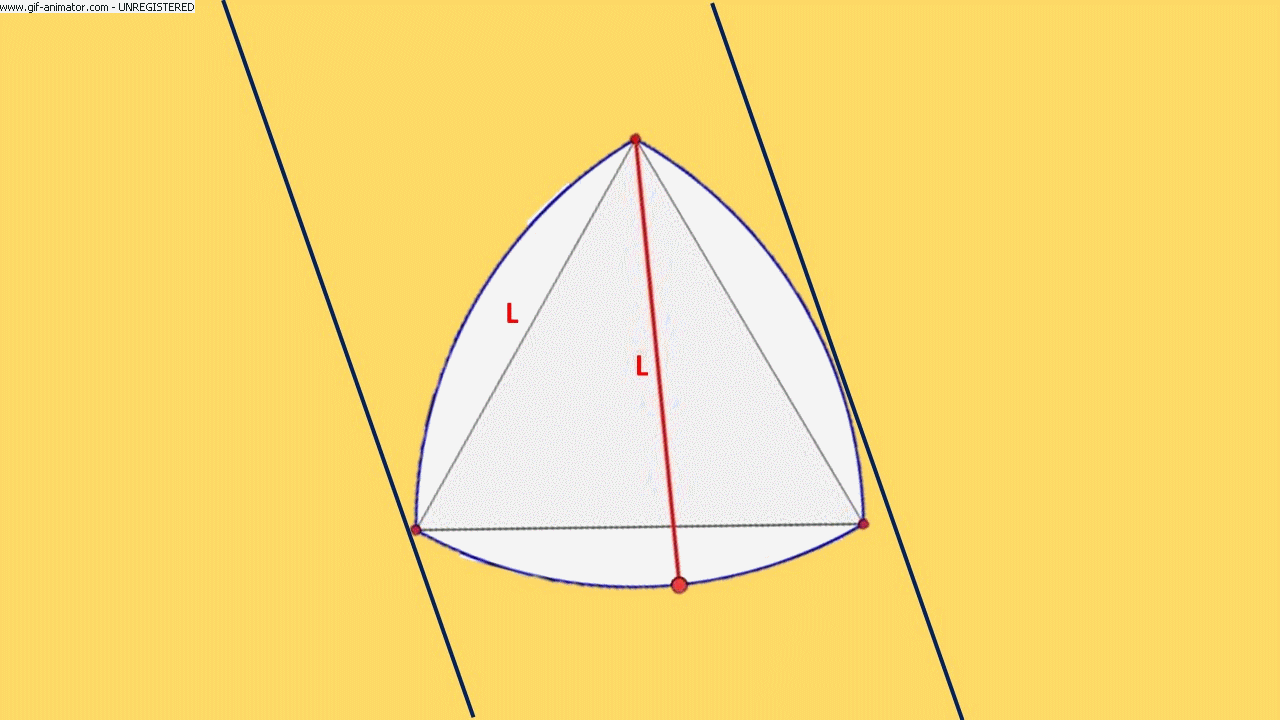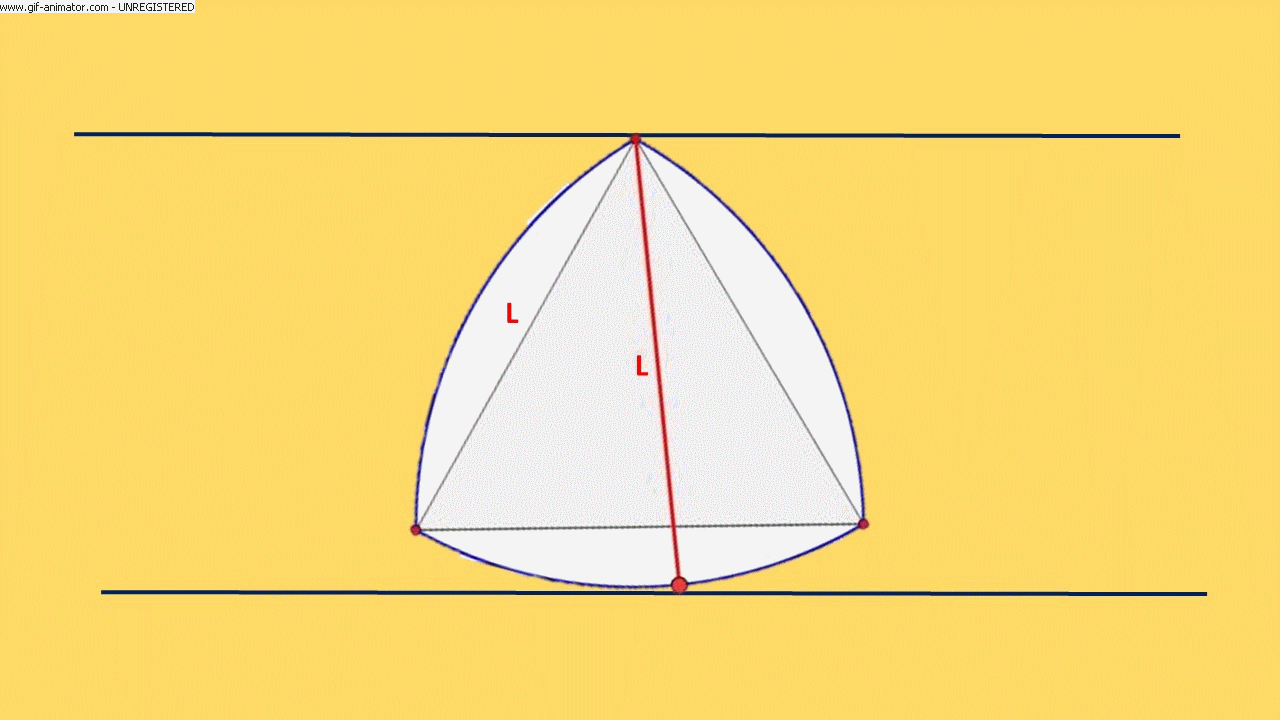
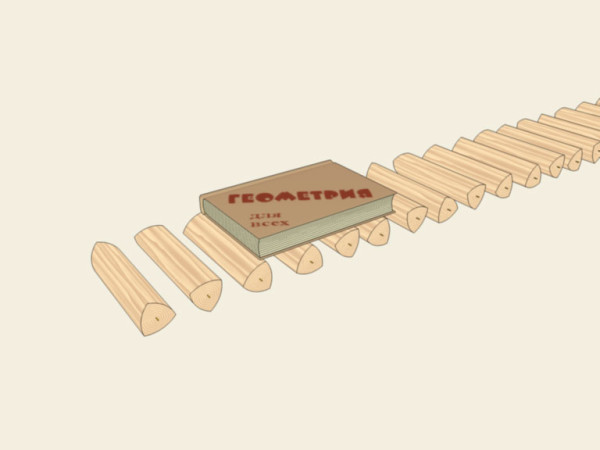
La larghezza è sempre uguale alla lunghezza del lato del triangolo equilatero quindi, se costruiamo dei rulli che hanno per sezione tale curva, e facciamo rotolare un libro su di essi, questo lo farà restando perfettamente orizzontale.

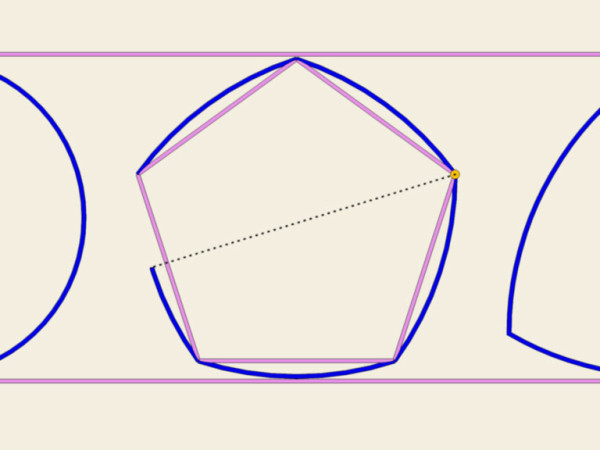
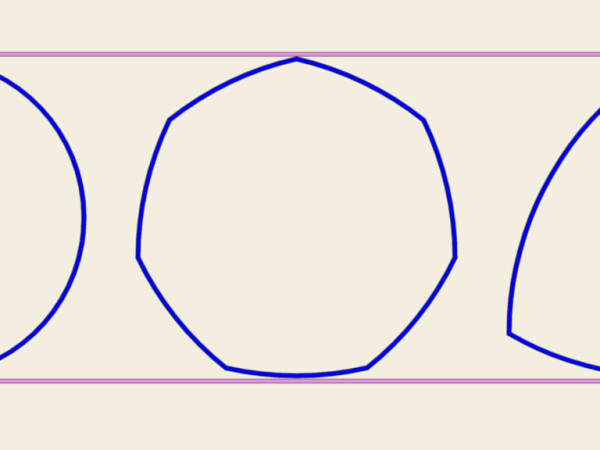
Una simile figura la possiamo costruire non solo partendo da un triangolo equilatero, ma da qualunque altro poligono regolare con numero di lati dispari (pentagono, ettagono, ecc…)

La cosa strabiliante è che, con delle ruote siffatte, si riesce ad andare tranquillamente in bici…

 

...oppure a cimentarsi in altri strambi e fantasiosi utilizzi:

Ditemi se non è una cosa da rimanere a bocca aperta! Sembra magia e, invece è semplicemente geometria!!

A questo punto pensavo che la lezione fosse finita e, invece, stava per iniziare la parte più divertente e stimolante: quella in cui ci è stato spiegato che, con un righello e un compasso, possiamo costruire INFINITE figure ad ampiezza costante!

Infatti è sufficiente tracciare un numero a caso di rette che si intersecano tra di loro e, prendendole due a due, puntare il compasso nell’intersezione e disegnare l’arco di cerchio compreso tra di esse. Il raggio del primo arco di cerchio lo scegliamo a caso, dopodiché, ogni arco successivo lo si inizia dal punto in cui termina il precedente. Vediamo come:

Tra le infinite figure con la stessa ampiezza, il cerchio è quello con area massima, il triangolo di Reuleaux quello con area minima.

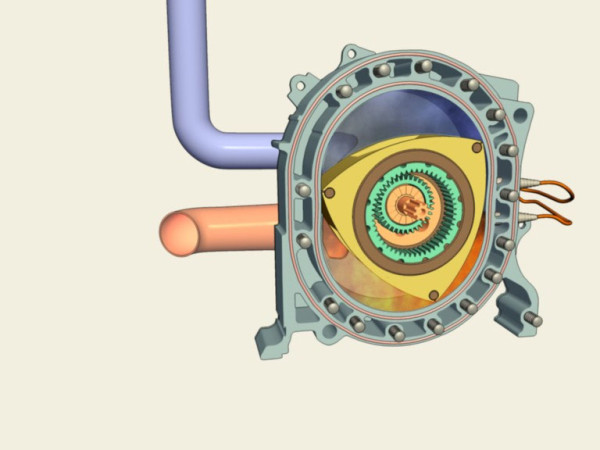
Tutto bello, starete pensando, ma è solo un divertente gioco per bambini… e invece il triangolo di Reuleaux ha impensabili applicazioni tecniche. Per esempio nei motori rotativi, il rotore ha questa forma: tra di esso e le pareti si formano tre camere, ognuna delle quali è a turno una camera di combustione. Viene dunque introdotta la miscela di benzina che, grazie al movimento del rotore, viene compressa e poi, scoppiando, fa girare il rotore. Il motore rotativo non utilizza pistoni: la rotazione è direttamente trasmessa all’asse e non è quindi necessario usare l’albero di trasmissione.

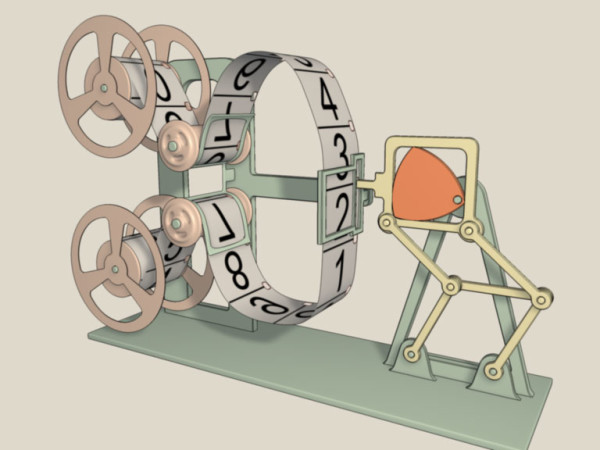
Un’altra sorprendente applicazione si ha nel meccanismo di proiezione di pellicole cinematografiche: al fine di avere sullo schermo delle immagini nette, bisogna che ogni fotogramma rimanga immobile per qualche istante e che il passaggio tra un fotogramma al successivo avvenga in un tempo molto più breve. Tutto questo 18 volte al secondo. Questo problema viene di fatto risolto proprio da un meccanismo che si basa sul triangolo di Reuleaux, inscritto in un quadrato, e su un doppio parallelogramma, che impedisce al quadrato di inclinarsi da un lato.

Infine una curiosità che ci ha raccontato il docente a fine lezione e che ha per protagonista il nostro amico Richard Feynman (sì, proprio lui, l’ideatore della QED, colui che pronunciò quel famoso discorso al Caltech nel 1959, considerato il precursore delle nanotecnologie). Feynman era membro della commissione d’inchiesta che indagò sulle cause della sciagura dello Space Shuttle Challenger nel 1986, che furono individuate negli errori di progettazione degli O-Ring (guarnizioni di gomma circolari usate per sigillare i razzi con il propellente per il lancio). Oltre al fatto che il materiale di cui erano composti perdeva resilienza alle basse temperature (questo il celebre video su YouTube), egli dubitò anche che fossero perfettamente circolari. Per questo, durante gli interrogatori, chiese come era stata verificata la rotondità di queste guarnizioni: alla risposta che erano stati misurati tre diametri e verificato che erano uguali, obiettò che la misurazione dei diametri non fosse sufficiente a stabilire, senza ombra di dubbio, che le guarnizioni fossero perfettamente circolari, perché anche le curve di Reuleaux hanno diametri costanti.

Ops… stavo dimenticando di rispondere alla domanda posta nel titolo… Franz Reuleaux (1829 – 1905) è stato un ingegnere meccanico tedesco che, pur non essendo un inventore come James Watt o un imprenditore come Werner Siemens, né uno scienziato come Faraday, giocò un ruolo cruciale nello sviluppo della meccanica verso la fine del XIX secolo: egli riconobbe l’importanza della scienza e della matematica nello sviluppo di un metodo razionale nella progettazione di macchine.

 

“Le forze della natura che quel progresso ci insegnò a ricercare sono quella meccanica, fisica e chimica; ma il prerequisito per il loro utilizzo era il pieno impiego della matematica e delle scienze naturali” (Franz Reuleaux).

 

 

 

QUI gli altri articoli scritti da Valentina