L'articolo che segue è inserito nella sezione d'archivio dedicata alla Meccanica Quantistica ed è composto dalla raccolta degli articoli che potete trovare QUI

 

Elettrodinamica quantistica: un nome che incute paura solo a pronunciarlo. Tuttavia, vale la pena non farsi spaventare. Con una fatica mentale non eccessiva si riesce a descrivere la maggior parte dei fenomeni dell'ottica di tutti i giorni e si comprende perfettamente come l'interazione tra luce e materia sia, in fondo, riconducibile a pochissime azioni sempre uguali a se stesse che coinvolgono due sole particelle: il fotone e l'elettrone. E' doveroso dire che la prima parte (prima di entrare nello spaziotempo) è decisamente più semplice. Dopo le cose si complicano un poco e l'attenzione deve crescere. Alla fine, però, vi sentirete veramente "sazi" e la meccanica quantistica vi apparirà molto meno incomprensibile anche se, sempre, priva di logica.

Non spaventatevi della sigla e del nome: l'elettrodinamica quantistica, spiegata da Richard Feynman, è accessibile a tutti e permette a tutti di comprendere (senza capire, per definizione) le interazioni che esistono tra elettromagnetismo (ossia  luce) e materia, praticamente tutto ciò che capita attorno a noi.

L’elettrodinamica quantistica (QED) studia sostanzialmente le interazioni tra gli elettroni e il campo elettromagnetico. Essi interagiscono tramite lo scambio di fotoni e di varie particelle virtuali, proprio quelle che nascono attraverso le fluttuazioni quantistiche. In parole più semplici e generali, la QED è la teoria più completa ed esauriente delle interazioni tra luce e materia. Lo scopo di questo lungo articolo (da leggere e da ponderare molto bene) è proprio quello di cercare di descriverla con le parole e i diagrammi più semplici possibili. Spesso definita come “gioiello della fisica”, essa riesce a spiegare una serie infinita di fenomeni e può essere considerata una delle teorie più esatte anche se rimane … incomprensibile.

Inizio questo arduo compito ringraziando colui che ha permesso, anche al mio modesto cervello, di riuscire a capire l’armoniosa semplicità che domina questo argomento, fondamentale per entrare completamente nel mondo della MQ. Mi riferisco, ovviamente a Richard Feynman e al suo corso di lezioni sull’elettrodinamica quantistica. Ringrazio, inoltre, tutti voi che cercherete di seguire il mio umile tentativo di imitare tale maestro. In ogni modo, sappiate che se risulterò comprensibile il merito è solo e soltanto del grande Richard.

Prima di prendere per mano un fotone e seguirlo nella sua vita così avventurosa e, spesso, inaspettata, fatemi sintetizzare un concetto che Feynman amava ripetere spesso e che io ho fatto mio (come spesso leggete nelle mie esternazioni). La maggior parte delle persone si interessa e vuole conoscere le ultime novità, relative ad argomenti che ancora non si conoscono. Poche volte si limita a cercare di sapere quello che si conosce con sufficiente sicurezza. Feynman diceva che la gente preferisce mangiare un cibo mezzo-cotto piuttosto che gustare manicaretti preparati a regola d’arte. Bene, l’elettrodinamica quantistica (QED) è un arrosto cotto al punto giusto, eppure è quasi sconosciuta ai più, che preferiscono cibarsi di teorie aleatorie ancora ben lontane dalla giusta cottura. Vi assicuro che parlare di una cosa ben stabilita come la QED è tutto fuorché noioso e/o difficile e riserva sorprese impreviste.

Il succo di tutto questo ramo della MQ è descrivere i rapporti tra la luce e la materia. Il che può ancora essere sintetizzato nelle interazioni tra fotone ed elettrone. In realtà, questo incontro è il primo e fondamentale abbraccio che avviene tra luce e materia. La QED non si ferma all’esterno del nucleo atomico, ma ha tutte le potenzialità per entravi dentro ed essere applicata a una folla di “particelle” ben diverse dagli elettroni, siano essi quark o gluoni. L’importante è seguire lo stesso "stile" quantico. A noi, comunque, basterà limitarci alla periferia atomica: c’è già abbastanza carne al fuoco e -soprattutto- ben cotta!

Non è male ricordare un altro requisito fondamentale necessario per seguire questi articoli. Un requisito evidenziato perfettamente da Feynman: l’importante è accettare di non capire cosa si sta studiando. Sembra un’assurdità, che però non è più tale entrando nella MQ. Quando Feynman iniziava a spiegare i concetti dell’elettrodinamica quantistica, di cui è stato il vero maestro sia scientifico che divulgativo, diceva chiaramente al suo pubblico che non avrebbe capito assolutamente cosa gli avrebbe spiegato. In effetti, erano le stesse cose che insegnava all’Università. Tuttavia, non vi erano problemi di preparazione e di istruzione, dato che i suoi studenti, per primi, non riuscivano a capire le sue spiegazioni. Erano quindi in buona compagnia. Ai volti dubbiosi e stupiti dell’uditorio, se non peggio, il grande scienziato aggiungeva subito che la ragione di quella incomprensione era una e una sola: lui stesso non capiva niente di quell’argomento!

Come già sappiamo, le motivazioni di questo discorso un po’ insensato sono insite nella MQ. Essa descrive la Natura in un modo del tutto estraneo al senso comune della logica e della razionalità. La meraviglia è che tutti gli esperimenti la confermano. Ne segue che se si vuole accettare la Natura bisogna anche accettare la sua assurdità. Il non capire qualcosa è il primo passo per la conoscenza delle leggi quantistiche che governano l’Universo.

Una strana particella

Vi sembrerà sciocco o inutile, tuttavia fatemi definire cosa intendiamo per fotone. Esso è una particella che trasporta l’informazione luminosa. A ognuna di loro è associata una “nota” o se preferite un codice numerico, che può essere grande o piccolo e che viene chiamato frequenza o colore. Sappiamo bene che per parlare di frequenza bisognerebbe considerare la luce come un’onda, ma per i nostri scopi possiamo benissimo limitarci ad associare a ogni  "tipo" di fotone  un certo numero (frequenza o colore) che lo caratterizzi.

Questo codice o nota si può sentire ogni qual volta un fotone colpisce un rivelatore. Il “tac” corrispondente sarà più o meno "forte" a seconda del codice del fotone. Ricordiamo anche che se un fotone colpisce un rivelatore non può colpirne anche un altro. In poche parole, non possiamo dividere il fotone in modo che metà colpisca un rivelatore e un’altra metà ne colpisca un altro. O tutto o niente. Il fotone è una particella indivisibile.

La luce (e quindi i fotoni) causa un numero incredibile di fenomeni che fanno parte del mondo “normale” e razionale. La luce si scompone in colori; si muove lungo una retta; si piega quando entra nell’acqua; si riflette quando colpisce uno specchio e l’angolo che la retta di arrivo fa con la perpendicolare al piano dello specchio è uguale a quello fatto tra quest’ultima e quella della luce riflessa; una lente concentra la luce; ecc., ecc.

Ebbene, tutti questi fenomeni “logici” e “comuni”, possono essere descritti,  in modo assurdo e non comprensibile, con la MQ, in particolare con l'elettrodinamica quantistica.

Riflettere o non riflettere, questo è il problema

Dedichiamoci a un fenomeno che ha ispirato molti pittori e che ha sempre affascinato le persone più romantiche: la riflessione parziale della luce da parte del mare o di un lago. Se si guarda all’interno dell’acqua si vede ciò che sta sotto la superficie (la luce deve quindi penetrare), ma, nello stesso momento, si vede anche il riflesso di qualche cosa che illumina la superficie (la Luna o il vostro volto o lo stesso Sole). Si può quindi facilmente concludere che parte della luce viene riflessa e parte viene rifratta, ossia penetra nell’acqua, anche se con un percorso "piegato" rispetto a quello con il quale l’aveva colpita.

La stessa cosa capita se accendete una lampada in casa in pieno giorno e guardate il vetro della finestra: vedreste sia ciò che sta succedendo all’esterno, ma anche il riflesso della lampada. Un’ulteriore prova che la luce è capace sia di attraversare il vetro sia di essere riflessa. Questo è un fenomeno che si può facilmente descrivere con l’ottica geometrica e con la fisica classica. Tuttavia, ben più generale (e assurda) è la spiegazione che si può dare attraverso la QED.

Innanzitutto, facciamo una semplificazione, che correggeremo più tardi: assumiamo che la riflessione sia dovuta solo alla superficie dell’acqua o del vetro. In realtà, dovremmo già iniziare a pensare che un pezzo di vetro è un sistema estremamente complesso, in cui una quantità incredibile di elettroni si agitano continuamente. Se vogliamo entrare nel mondo della QED, un pezzo di materia deve essere considerato in questo modo. Quando un fotone entra nel vetro interagisce con gli elettroni e compie una specie di frenetica danza. Tuttavia, il risultato finale è del tutto simile a quello che si ottiene considerando solo ciò che capita sulla superficie. Lo vedremo meglio successivamente.

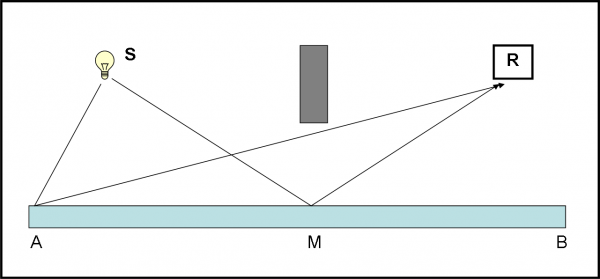
A questo punto siamo pronti a fare un esperimento ideato da Feynman. Ciò che ci occorre è un pezzo di vetro, due rivelatori di fotoni e qualche fotone con lo stesso codice, ossia con la stessa frequenza o colore. Un rivelatore R1 aspetta i fotoni che rimbalzano indietro e l’altro, R2, viene “inserito” dentro al vetro in modo da catturare quelli che entrano. L’esperimento è rappresentato in Fig. 1.

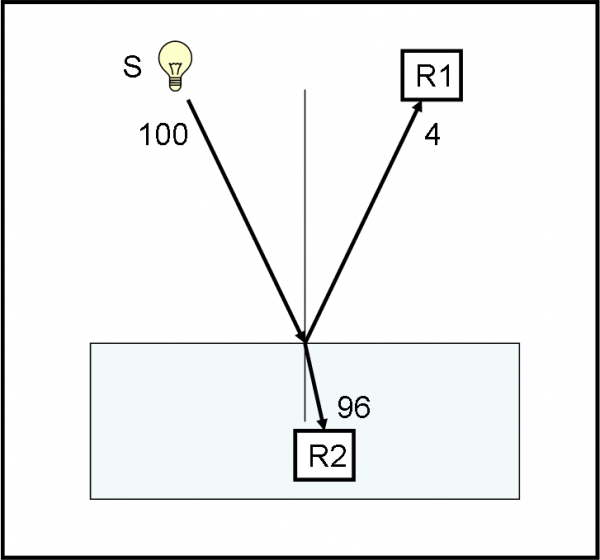
Lanciamo 100 fotoni dalla sorgente S. Poi andiamo a controllare cosa hanno ricevuto i due rivelatori R1 e R2. Il primo solo 4 e il secondo 96. Possiamo facilmente concludere che 96 fotoni sono penetrati nel vetro e 4 sono stati riflessi.

Niente di speciale? Ebbene no. Già questo risultato, dall’apparenza ovvia per quanto sappiamo dall’esperienza di tutti i giorni, impone una domanda imbarazzante: “Come fa un fotone a scegliere se andare in R1 o in R2?” Sembrerebbe una domanda assurda, che non merita una risposta. Ma, riflettendoci sopra, è invece essenziale e molto seria. Potremmo riformularla più correttamente: “Perché qualche fotone (4) finisce in R1 e molti altri (96) finiscono in R2?”.

I fotoni sono per definizione perfettamente uguali e hanno anche lo stesso numero che li identifica (la stessa frequenza). Non ha alcun senso che si comportino in maniera diversa. La QED va a nozze. La domanda è assurda? Perfetto. Si può tranquillamente dare una risposta altrettanto assurda, ma attraverso una teoria ineccepibile. Iniziamo il grande gioco della MQ e seguiamo Alice, ops… i fotoni!

Prima, però, cerchiamo con un ultimo tentativo disperato di azzardare qualche altra teoria che rimetta le cose su un piano normale. La domanda è assurda, ma la risposta potrebbe rimetterla nel senso comune.

Ad esempio, potremmo pensare che il vetro sia formato, per la maggior parte, da buchi (il 96%) che permettono alla luce di infilarsi all’interno. Solo il 4% è solido ed è quello che riflette qualche fotone. La teoria è facilmente distruttibile, soprattutto dopo aver pulito e levigato perfettamente la superficie del vetro. Niente cambia e i fotoni continuano a comportarsi in modo diverso. No, la faccenda non può risolversi con una strana struttura del vetro.

Se la colpa non è del vetro, può darsi che sia dei fotoni. Loro sembrano identici e invece hanno una qualche caratteristica intrinseca diversa. Come fare a provarlo? Facile: basta inserire prima del blocco di vetro, alcuni “filtri” anch’essi formati da superfici riflettenti. Se un fotone è del tipo “che passa”, quelli che arrivano sulla nostra superficie devono essere solo quelli che riescono a entrare. E, invece, capita tutto esattamente come prima. Di 100 fotoni che arrivano, 96 fotoni attraversano il pezzo di vetro, ma 4 continuano a essere riflessi.

La scelta del fotone

Non ci rimane che entrare nel mondo dell’assurdo e dire che è impossibile conoscere cosa decide di fare il singolo fotone. Può “scegliere” di andare dritto o rimbalzare, ma è una decisione tutta sua che non potremmo mai conoscere. Tuttavia, qualcosa può essere conosciuto, ossia la percentuale di fotoni che tornano indietro rispetto a quelli che avanzano.

Non possiamo prevedere quale fotone fa una scelta o l’altra, però possiamo dire che il 4% torna indietro e il 96% va avanti. Vi rendete conto di quello che abbiamo detto? La fisica, quella scienza che descrive e spiega in modo esatto, è costretta a calcolare soltanto la probabilità di un evento. In altre parole, ancora più pesanti, la Natura ci permette solo di calcolare una probabilità. Assurdo, veramente assurdo!

Tuttavia, questo risultato è ancora niente rispetto a quello che ci attende, complicando un poco l’esperimento. Al posto di una sola superficie riflettente, ne prendiamo due. Ciò si ottiene con una lastra di spessore molto piccolo in cui la superficie superiore e quella inferiore siano perfettamente parallele.

Sappiamo già molto bene che alcuni fotoni si riflettono sulla superficie d’entrata, ma altri possono riflettersi su quella di uscita (ricordiamoci che, per il momento, abbiamo considerato che la riflessione avvenga solo su una superficie). Poniamo il rivelatore R2 al di sotto della lastra sottile, come rappresentato in Fig. 2. Facciamo un po’ di conti, accettando l’assurdità che i fotoni possano scegliere e che noi ci si possa limitare solo a un calcolo delle probabilità. Dunque, la prima superficie rifletterebbe solo 4 fotoni e 96 dovrebbero passare (ne abbiamo avuto conferma diretta). I 96 che entrano colpiscono la seconda superficie e dovrebbero subire lo stesso fenomeno. Il 4% dei 96 dovrebbe nuovamente essere riflesso. Senza voler andare troppo nel sottile, i fotoni o sono uno o zero e non frazioni dell’unità: ci dobbiamo aspettare che sul rivelatore R1 arrivino o 7 o 8 fotoni dei 100 inviati.

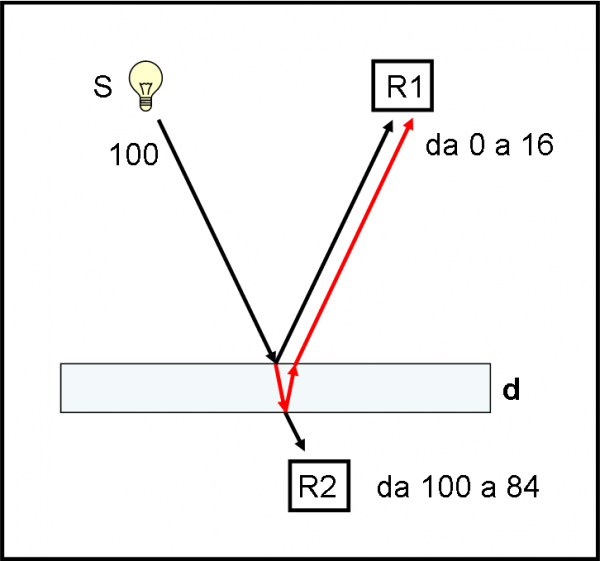
Già in questo modo abbiamo dovuto fare uno sforzo di illogicità, accettando di ragionare solo in termini di probabilità di fronte a un fenomeno fisico che la Scienza dovrebbe poter spiegare e calcolare perfettamente.

No, non saltate sulla sedia, c’era da aspettarselo: i fotoni ricevuti da R1 sono molti di più, ben 16! Ciò è ulteriormente confermato dal fatto che R2 ne riceve solo e soltanto 84. Non si può nemmeno sperare che i fotoni si siano, in qualche modo, moltiplicati. Vi rendete conto che stiamo azzardando sempre più risposte fuori dalla logica comune? Bene, bene… vuol dire che stiamo seguendo Alice.

Tuttavia, quel 16% ci mette veramente in crisi, pur con tutti gli sforzi che stiamo facendo. Non solo dobbiamo continuare a parlare in termini di probabilità, ma dobbiamo anche accettare il fatto che la seconda superficie sembra amplificare l’attesa probabilistica.

Non basta ancora, però. Proviamo a cambiare la lastra di vetro con delle altre del tutto simili come materiale. I numeri sembrano prenderci in giro. A volte in R1 arrivano solo 1 o 2 fotoni in totale. Altre volte non ne arriva nessuno. Mamma mia, non ci capiamo più niente!

Cerchiamo di ragionare e di dare  regolarità ai nostri esperimenti. Sì, in effetti, qualcosa è cambiato da una volta all’altra. Anche se di pochissimo, lo spessore della lastra è variata. Possiamo tentare di concludere che il numero di fotoni riflessi dalle due superfici dipende essenzialmente dalla loro separazione. Piano, piano... va bene accettare tutto, ma cerchiamo di fare un po’ di ordine ed eseguire ulteriori esperimenti mirati allo scopo.

Cominciamo con una lastra sottilissima, il cui spessore possa considerarsi praticamente zero. R1 riceve mediamente soltanto 1 fotone. Aumentando lo spessore, appena appena, ci sentiamo un po’ meglio: R1 riesce a ricevere proprio 8 fotoni, il numero che ci saremmo aspettati all’inizio. La speranza è di breve durata. Se inseriamo una lastra più spessa, dell’ordine di 10^-7 metri, ossia 10^-4 millimetri, o, ancora, un decimo di micron (chiamiamola spessa!), il risultato torna a sbigottirci e i fotoni tornano a essere 16. Un valore massimo però. Aumentando ancora lo spessore il numero inizia a decrescere per tornare nuovamente a 1 o addirittura a zero. Continuando ad allargare la lastra, si ripete il ciclo e via dicendo. Insomma, lo spessore della lastra cambia la probabilità di avere un certo numero di fotoni riflessi e lo fa in modo perfettamente periodico. Anche la probabilità comincia a farci vedere cose assurde.

Possiamo, però, cercare di estrarre una qualcosa di comprensibile o -meglio- di logico in questo fenomeno: andando da un valore minimo a un valore massimo dei fotoni riflessi, il valore medio è proprio quel numero 8 che sarebbe stato plausibile per un ragionamento normale. Beh… è già qualcosa. Tuttavia, il valore 8 si ottiene , in realtà, solo due volte per ogni ciclo, quando lo spessore raggiunge un ben determinato valore o un suo multiplo esatto.

Feynman dice, giustamente, che si comporta come un orologio, dato che le lancette segnano una certa ora solo due volte in 24 ore. Questo risultato ha un certo senso matematico e può essere rappresentato attraverso la Fig. 3, dove in ascissa mettiamo lo spessore della lastra di vetro e in ordinata la percentuale di fotoni  che raggiungono R1. Come, ormai, ci aspettavamo, data la periodicità del risultato, la curva è una sinusoide, composta da una serie ininterrotta di massimi e minimi (vedete come serve lo studio delle funzioni?).

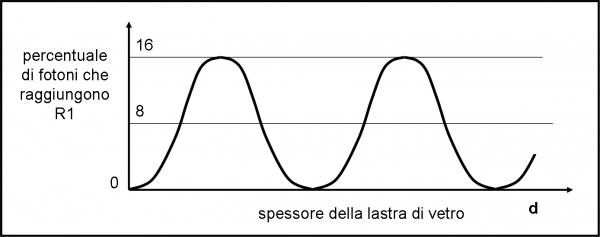
Decidere dopo... ciò che si sta facendo prima

Restiamo però con i piedi per terra (finché ci riusciamo). Stiamo accettando come logico e matematico un qualcosa che è di per sé un fenomeno completamente assurdo. Il numero di fotoni riflessi dovrebbe dipendere dalle caratteristiche intrinseche dei fotoni o, al più, dalla composizione del vetro. Il fatto che, aumentando o diminuendo la distanza tra le superfici parzialmente riflettenti, cambi la capacità delle stesse superfici di riflettere i fotoni, resta una vera assurdità nella logica comune. Ma la cosa è ancora più assurda. La seconda superficie riesce ad annullare ciò che dovrebbe comunque succedere nella prima.

Infatti, se accettiamo che la prima ne rifletta sempre il 4%, l’aggiunta della seconda superficie, qualsiasi sia la distanza dalla prima, potrebbe aumentare oppure no il numero dei fotoni riflessi (e già questo è alquanto strano), ma non certo riuscire ad annullare quelli della prima. Sembrerebbe che i fotoni della prima riflessione non solo scelgano dove andare, ma decidano in base a ciò che capiterà ai loro fratelli nella seconda riflessione. In altre parole, ciò che capita nella seconda superficie sembra influire su ciò che capita nella prima, anche se avviene dopo. Questo fatto è veramente all’altezza del mondo di Alice e scombussola tutte le nostre convinzioni scientifiche di causalità e di freccia del tempo. Pensiamoci bene e ci troveremo veramente molto frastornati.

E’ il momento di inserire il coltello nella piaga ancora più a fondo. Come? Basta aggiungere una terza superficie e vedere i risultati. I numeri cambiano di nuovo e sembra che si debba accettare sempre di più il fatto che, per sapere come comportarsi nella prima superficie, i fotoni debbano sapere come si comportano gli “altri” nel passaggio di tutte le superfici. Un caos terribile, degno di un pazzo. E invece, tutto ciò è esprimibile e spiegabile matematicamente. Questa è la QED e questo vuol dire peché è assolutamente incomprensibile anche per un genio come Feynman!

Fatemi ancora ripetere il concetto di base: “la scelta di un fotone quando incontra la prima superficie dipende da quali saranno le decisioni degli altri fotoni di fronte alle altre superfici”. Una decisione corale che sembra non tener conto del tempo e del suo scorrere.

Attenzione. Uno potrebbe cercare di rispondere a queste assurdità, considerando la luce come onda e scartando l’ipotesi delle particelle. Purtroppo le prove giocano a sfavore di questa scappatoia: se diminuiamo progressivamente l’intensità della luce, ci rendiamo conto che i rivelatori continuano a ricevere segnali della stessa intensità (ossia con lo stesso codice di frequenza se il colore è uno soltanto). Ciò che cambia è il numero di segnali ricevuti nell’unità di tempo. Ciò dimostra, al di fuori di ogni dubbio, che si stanno misurando particelle che o esistono o non esistono. Possono diminuire di numero ma non cambiare la loro caratteristica.

Non pensiate che tra poco capiremo perché capita tutto ciò. Nessuno è in grado di farlo. Tutto ciò che si riesce a fare è calcolare esattamente, attraverso una teoria perfetta, la probabilità che la luce sia più o meno riflessa da una superficie. Nessuno è ancora riuscito a spiegare perché e come un fotone decide di comportarsi. La QED ci permette, però, di calcolare esattamente la probabilità di ottenere un certo risultato a seconda delle condizioni in cui siamo.

Feynman dà particolare risalto all’esempio della riflessione parziale (un perfetto esempio per spiegare come agisce la teoria), ma lo stesso tipo di trattazione e di spiegazione si applica a TUTTI i fenomeni in cui vi è interazione tra luce e materia. Questo fa della QED un gioiello fisico assoluto, assurdo -se volete- ma preziosissimo!

Per potere effettuare il calcolo dell’esatta probabilità (l’unica cosa possibile) è necessario introdurre una semplice freccia, di direzione e lunghezza variabili, e munirsi di un foglio di carta. Se poi riuscissimo a scovare anche un cronometro, non sarebbe male, ma può anche bastare un semplice orologio calibrato adeguatamente. La semplicità delle scoperte eccezionali!

Le frecce si abbracciano

Disegniamo, allora, una freccia e assumiamo che la probabilità che accada un certo evento sia uguale al quadrato della lunghezza della freccia, come mostrato in Fig. 4. Concetto difficile? direi proprio di no e segue una definizione che già avevamo dato nella descrizione del fenomeno della doppia fenditura. Quanto sarà lunga la freccia che indica la probabilità che un fotone si rifletta sulla prima superficie? Sappiamo che la probabilità è del 4%, ossia 0.04. La freccia ha, allora, una lunghezza che è la radice quadrata di 0.04, ossia 0.2. Infatti: 0.2² = 0.04. Matematica veramente elementare, ma che ci regala il mezzo per descrivere come lavora la QED. Sembra impossibile, ma è proprio così.

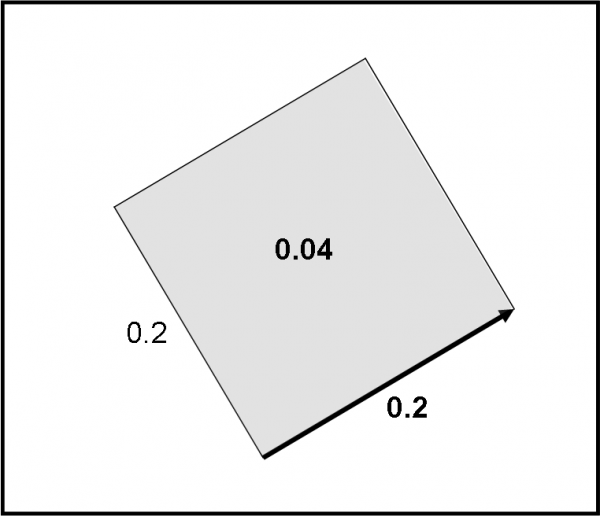
Dedichiamoci, allora, all’esperimento proposto da Feynman attraverso la lastra di vetro sottile.

Ricordiamo che la conclusione è stata che la probabilità finale dei fotoni riflessi varia da 0 a 16%. Come possiamo rappresentarla in termini di “freccia”? Essa dovrebbe variare in modo tale che il suo quadrato passi da 0 a 16, al variare dello spessore della lastra di vetro. Come già detto la volta scorsa, continuiamo ad assumere che la riflessione avvenga o sulla prima superficie o sulla seconda. Ciò vuol dire che esistono due sole possibilità affinché un fotone raggiunga il rivelatore R1: o attraverso la prima o attraverso la seconda superficie. In qualche modo le due probabilità ad esse relative devono “sommarsi”. La cosa più ovvia è, allora, disegnare due frecce, ognuna relativa a una delle due riflessioni e poi cercare di combinarle in modo che il quadrato della freccia finale sia proprio la probabilità finale dei due eventi. Possiamo già estrapolare questo modo di agire, dicendo che se gli eventi fossero tre, dovremmo combinare tre frecce e via dicendo.

Vediamo, allora, come si possono combinare le frecce (ognuna delle quali si porta dietro la sua probabilità, ossia il suo quadrato) in modo da ottenere il risultato voluto, ossia una freccia che abbia per quadrato la probabilità finale.

Non preoccupiamoci: il sistema lo conosciamo ormai molto bene attraverso le grandezze vettoriali. Ricordate come si sommano o si sottraggono i vettori? Beh… andate a ripassarlo, ad esempio, QUI o addirittura nella Fisica addormentata nel Bosco. In definitiva vale la famosa regola del parallelogramma.

Combiniamo, quindi, le nostre frecce-probabilità proprio come si agisce sommando i vettori. Usiamo la Fig. 5 per spiegarci meglio. Vogliamo “combinare” la freccia x con la freccia y. Spostiamo il vettore y, parallelamente a se stesso, senza cambiargli direzione, verso e modulo, fino a che la sua “coda” coincida con la “punta” di x.  A costo di essere noioso, ricordo ancora che ogni freccia è legata alla possibilità che un certo evento possa accadere.

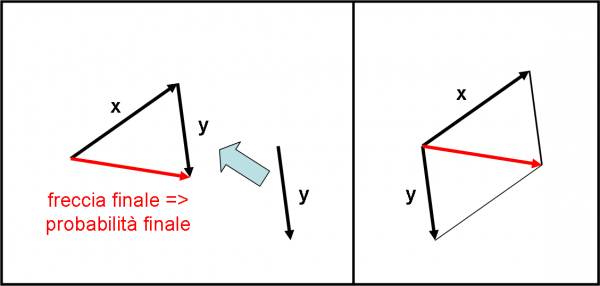
A questo punto non ci rimane che unire la coda della prima freccia con la punta della seconda. La freccia che si ottiene è la combinazione delle due. Avete notato sicuramente  che non abbiamo fatto altro che sommare i vettori x e y. Il vettore finale è la somma vettoriale di x e y.

Feynman fa un bellissimo paragone con la danza. Ogni singola freccia ci indica i passi da fare, volta per volta; la freccia conclusiva indica lo spostamento finale alla fine della danza, ossia il passo che si sarebbe dovuto fare per  raggiungere la posizione finale con un solo spostamento.

La Fig. 6 ci fa vedere una combinazione in cui abbiamo a che fare con un maggior numero di frecce. Il risultato si ottiene seguendo la regola già descritta. Notate, comunque, che non è importante l’ordine con cui si combinano le frecce: la freccia finale è sempre la stessa.

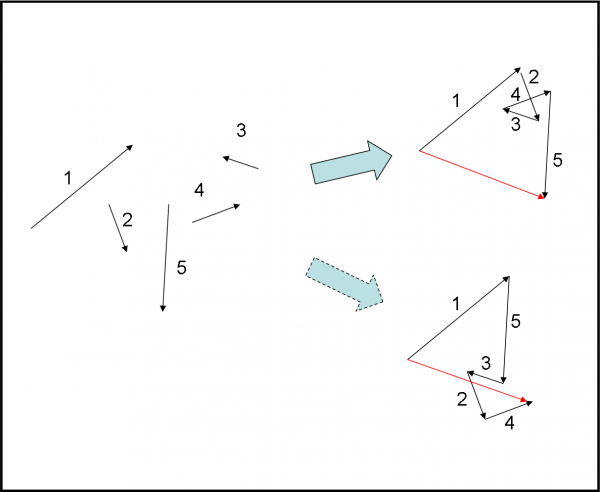
Procuriamoci un cronometro

Tutto molto bello e soprattutto facile… ma come definire la lunghezza delle singole frecce e -soprattutto- la loro direzione? Per entrare nel caso dell’esperimento della lamina di vetro, le singole frecce sono legate alla probabilità, come già detto, della singola riflessione (nella prima e nella seconda superficie) e la freccia finale alla probabilità della doppia riflessione.

Cominciamo con la lunghezza della freccia. Per la prima superficie, sappiamo già cosa rappresenta: un valore tale che il suo quadrato sia 0.04 (4%), ossia 0.2. La seconda superficie, indipendentemente dal risultato finale che abbiamo osservato, DEVE comportarsi nello stesso modo e quindi anche la freccia relativa deve avere una lunghezza uguale a 0.2.

Il vero problema è quindi definire in modo corretto la direzione di ogni freccia. Solo lei “deciderà” cosa si ottiene dopo la combinazione delle frecce, ossia qual è la somma dei vettori. Ricordiamoci, infatti, del moto circolare uniforme. Due frecce aventi uguale lunghezza (velocità tangenziale) danno luogo a una differenza che non è nulla, ma è uguale all’accelerazione centripeta. Questo semplice esempio ci mostra, ancora una volta, che per poter parlare di MQ bisogna avere una grande dimestichezza con la fisica classica. In altre parole (ripetendomi ancora una volta): per essere Picasso non basta disegnare quadrati e triangoli qualsiasi, ma si deve avere una sapiente conoscenza della pittura dei tempi precedenti.

Feynman ci insegna a calcolare la direzione delle frecce attraverso una geniale descrizione che fa uso di un cronometro speciale, la cui lancetta ruota seguendo il movimento del fotone. Nel caso che sia un fotone “rosso”, il cronometro compie circa 1.440.000 giri per ogni metro percorso dal fotone. Non vi sarà sfuggita una “strana” coincidenza: un giro corrisponde a circa 700 nanometri  (1 nanometro = 10^-9 metri) percorsi dal fotone. Guarda caso questo valore è proprio la lunghezza d’onda della luce rossa… Boccaccia mia stai zitta! Avevo promesso di non interagire con la fisica classica e devo mantenere la promessa.

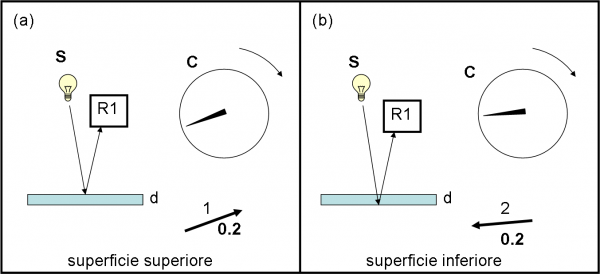
Facciamo partire il cronometro ogni volta che un fotone esce dalla sorgente. Anche se il nostro amico viaggia molto velocemente, il cronometro riesce a stargli dietro e la lancetta gira visibilmente sul quadrante. Schiacciamo con decisione e prontezza il pulsante all’arrivo del fotone in R1 (sempre che sia uno di quelli che arriva su R1, ovviamente). Se il fotone giunge a destinazione riflettendosi sulla prima superficie, dobbiamo considerare come direzione quella della lancetta, ma invertire il verso, come rappresentato in Fig. 7a.

Se, invece, il fotone arriva in R1 riflettendosi sulla seconda superficie, la direzione è sempre quella della lancetta, ma il verso rimane quello che è (Fig. 7b). Ovviamente, il fotone attraversa due volte la lastra molto velocemente (la lastra è stata scelta veramente sottile) e quindi arriva su R1, dopo la riflessione sulla seconda superficie, con una direzione della lancetta ben poco diversa da quella che aveva nel caso del fotone precedente. La lunghezza di entrambe le frecce resta quella che è, ossia 0.2, dato che entrambi gli eventi hanno la probabilità del 4% di avvenire.

In Fig. 8 non ci resta che combinare le frecce con il metodo descritto prima e ricavare la freccia finale, il cui quadrato non è altro che la probabilità finale di avere una riflessione, non importa in quale superficie siano avvenute le riflessioni. E’ facile notare che la freccia rossa finale è estremamente corta e quindi la probabilità che capiti l’evento complessivo è veramente vicina a zero (0.0025).

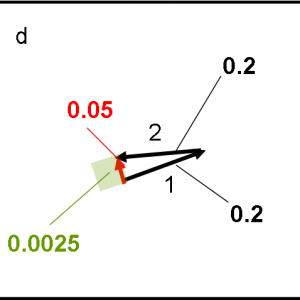
Ridendo e scherzando (e senza aver capito perché) siamo riusciti a calcolare graficamente la probabilità finale di una doppia riflessione. Diventa ovvio dimostrare, in questo modo, che due probabilità possono dare una probabilità finale nettamente più bassa che la “banale” somma delle due. In particolare, più bassa anche di quella della sola prima riflessione (che è del 4%), cosa che continua ad andare al di là della nostra comprensione. Il procedimento, però, funziona, anche aumentando lo spessore d della lastra? Non ci resta che provare.

Le frecce seguono lo spessore e tutto torna

Aumentiamo un po’ lo spessore d portandolo a d1. Il fotone che si riflette nella superficie superiore non cambia assolutamente e la sua freccia resta tale e quale. Il fratellino che si riflette su quella inferiore deve invece percorrere un tragitto più lungo e mentre lo fa il cronometro continua a girare. Quando, finalmente, arriva in R1, la lancetta si è spostata “parecchio” rispetto al caso precedente (Fig. 9a,b).

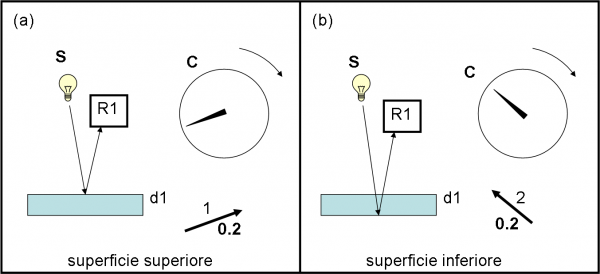
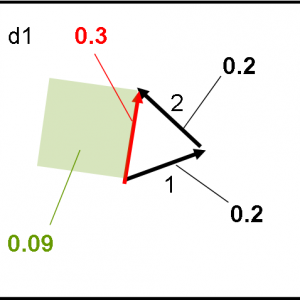
Non ci resta che fare il giochetto che ormai conosciamo bene e che è riportato in Fig. 10. Accidenti! Le cose sembrano proprio funzionare. La freccia finale è diventata più lunga di quelle che l’hanno costruita. La sua lunghezza è, adesso, di 0.3, il che comporta una probabilità finale di 0.09, ossia del 9%. L’aumento dello spessore ha dato molta più possibilità all’evento “riflessione”. Sembra che lo spessore abbia convinto i fotoni a scegliere la strada del “rimbalzo”.

Le cose, però, si fanno ancora più interessanti se aumentiamo ancora lo spessore fino a un certo livello “critico”. Ridisegniamo nuovamente le figure anche se non ce ne sarebbe bisogno. Ma, avevamo promesso di essere elementari e continuiamo in questa direzione. La Fig. 11a,b mostra la situazione del cronometro, della sua lancetta e della freccia relativa. Senza sorprenderci più di tanto (ci siamo abituati alla descrizione senza volere per forza capire), notiamo che la lancetta ha percorso esattamente mezzo giro in più. D’altra parte è logico.

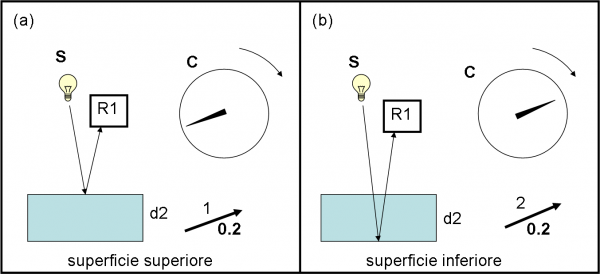
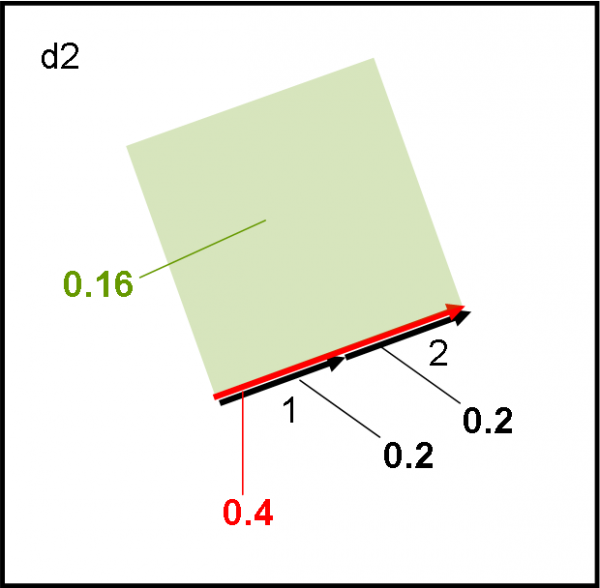
Il tragitto del fotone che rimbalza sulla seconda superficie è aumentato. E’ un gioco da ragazzi disegnare la Fig 12 dove eseguiamo la composizione delle due probabilità. Ci accorgiamo che le due frecce relative vanno nella stessa direzione e che, di conseguenza, la freccia finale ha una lunghezza esattamente uguale al doppio di quella singola. In altre parole, sommiamo proprio i moduli dei due vettori, dato che la direzione è la stessa.

Beh… quante volte abbiamo ottenuto lo stesso risultato sommando velocità o altre grandezze vettoriali? In conclusione abbiamo una freccia finale rossa che ha una lunghezza di 0.4. Il suo quadrato è 0.16, ossia la probabilità che un fotone rimbalzi verso R1 è salita al suo massimo, il 16%. Il metodo funziona perfettamente.

Ricapitoliamo: non sappiamo perché (e preferiamo perfino soprassedere su alcune assurdità sconvolgenti, come quella che sembra dirci che i fotoni che effettuano la prima riflessione decidano di farlo a seconda di come si comporteranno DOPO che i loro amici arrivano sulla seconda superficie) tuttavia, abbiamo escogitato (ops… Feynman ha escogitato…) un metodo di una semplicità disarmante che ci permette di calcolare, comunque, la probabilità finale che un fotone ha di arrivare su R1. Noi l’abbiamo seguito graficamente e senza introdurre la “matematica”, ma esistono formule estremamente complesse che potrebbero definirlo in modo ineccepibile. Ricordiamoci che la QED si basa su una perfetta matematica, ma ha la gentilezza di farsi comprendere anche attraverso operazioni alla portata di tutti.

Potremmo andare avanti aumentando lo spessore, ma il risultato è ormai banale. Se lo spessore raggiunge una certa dimensione la lancetta del cronometro, relativa al fotone che subisce la riflessione inferiore, arriva, nuovamente, ad avere la stessa identica direzione del fotone che è rimbalzato subito. Eseguendo l’inversione della prima freccia, troveremo un risultato ormai ovvio ma pur sempre imbarazzante: la probabilità finale torna a essere zero e avanti così con una periodicità perfetta, così come è perfetta la rotazione della lancetta del cronometro. La Fig. 3 dell’articolo precedente è confermata in pieno!

Alcune considerazioni aggiuntive. Abbiamo visto che le direzioni assunte dalla lancetta nei due casi di riflessione (sulla prima e sulla seconda superficie) anticipano il risultato. Se hanno la stessa direzione e verso, otteniamo una probabilità nulla. Se hanno la stessa direzione, ma verso opposto, otteniamo una massima probabilità (16%). Se le direzioni delle lancette formano un angolo di 90°, l’applicazione del teorema di Pitagora ci dice che la freccia finale è l’ipotenusa di un triangolo isoscele. Ne deriva, subito, che la probabilità finale (quadrato dell’ipotenusa) è il doppio della probabilità di un cateto, ossia di una singola riflessione. Ne segue che  la probabilità finale è data da 2･(0.2)² = 2･0.04 = 0.08, proprio il valore che sarebbe sembrato, a prima vista, il più logico! Lascio a voi la figura che sintetizza questa situazione peculiare che, come già detto, capita due volte a ogni giro della lancetta del cronometro.

Inoltre, teniamo ben presente che la prima freccia rimane sempre la stessa ed è solo la seconda che, pur mantenendo costante la lunghezza, esegue una (o più) rotazioni complete all’aumentare dello spessore.

Fermiamoci un attimo e riassumiamo le idee, dando magari qualche definizione “tecnica”. La lunghezza della freccia viene indicata come ampiezza della probabilità. Una definizione che già conosciamo bene avendone parlato nel caso della doppia fenditura (ricordate). In particolare, segue immediatamente che la probabilità di un evento è uguale al quadrato dell’ampiezza di probabilità. Penso che non sfugga a nessuno l’analogia con un’onda, un’onda di probabilità… come d’altra parte già ci aveva mostrato la Fig. 3. Faccio questa piccola concessione alla fisica, più o meno classica, proprio perché fa già parte della MQ.

Bisogna poi che si sia veramente onesti, così come lo è stato Feynman. In realtà non abbiamo veramente imparato a calcolare la probabilità di un evento (o meglio ancora, l’ampiezza di probabilità di un evento), ma, più giustamente, abbiamo “provato” (con successo) a trovare l’ampiezza di probabilità il cui quadrato sia proprio la probabilità che un evento ha di verificarsi. Tra le due frasi vi è una profonda differenza concettuale.

Coloriamo le frecce

A questo punto, merita tornare sul famoso codice o numero o frequenza che caratterizza un fotone. Esso determina anche il suo colore. Facciamo, allora, un altro semplice esperimento: stendiamo uno strato sottile di olio sul pavimento, magari proprio quello molto sporco -e praticamente nero- della nostra automobile. Illuminiamolo con fotoni che hanno tutti lo stesso codice, ad esempio quello  rosso. Cosa vediamo? Delle zone rosse che si mischiano a zone quasi completamente nere. Come si spiega questo fenomeno, sulla base di quanto abbiamo appena descritto?

Non è certo difficile trovare una descrizione logica a seguito di una spiegazione incomprensibile. Lo strato d’olio si comporta come uno strato di vetro ed è sicuramente lontano dall’avere lo stesso spessore in ogni sua parte. Cosa succede allora? Nelle zone in cui è più sottile (o più spesso), la doppia riflessione può portare al valore zero della probabilità di riflessione e, quindi, nessun fotone torna indietro: l’olio rimane scuro. Dove, invece, lo spessore è più grande (o più piccolo), la doppia riflessione raggiunge la massima probabilità di accadere e quindi un bel numero di fotoni rossi rimbalza facendo assumere all’olio un colore rosso più o meno acceso. Dato che lo spessore cambia in modo abbastanza continuo, si vedranno bande rosse separate da bande nere relativamente più strette.

Analoga situazione capita se usiamo fotoni blu (codice diverso). Si ottengono, per la stessa identica ragione, bande blu separate da bande nere.

Proviamo, adesso, a inviare sullo strato d’olio sia fotoni rossi che blu. Il risultato è un bellissimo spettacolo di bande blu, rosse , quasi nere e altre di colori intermedi. Come mai? Elementare (o quasi)! Il codice del blu è diverso dal codice del rosso: il primo è decisamente maggiore ossia la sua frequenza è maggiore. Ciò vuol dire che la freccia del fotone blu gira più velocemente di quella del fotone rosso. Ammettendo (e non vediamo proprio perché non si debba farlo) che il comportamento della curva di probabilità sia la stessa per entrambi i fotoni, la luce blu riesce a completare il proprio ciclo probabilistico durante una variazione di spessore minore rispetto a quella necessaria al completamento di un ciclo della luce rossa.

Graficamente (e più facilmente) questa situazione è mostrata in Fig. 13 che altro non è che la Fig. 3 in cui sono stati sovrapposti i due tipi di fotone. Per un certo spessore, ad esempio, la probabilità dei fotoni blu di giungere in R1 ha già raggiunto il valore massimo, mentre quella dei rossi è ancora a “mezza strada”. Vi sono molti tipi di combinazione… Può capitare che il blu sia al massimo e il rosso al minimo (vediamo solo luce blu), oppure sia il blu che il rosso arrivano al massimo (mix perfetto dei due colori), oppure è il rosso che raggiunge il massimo mentre il blu è al minimo. Capita, ovviamente, anche che entrambi i colori siano al minimo del ciclo (colore nero, nessuna riflessione).

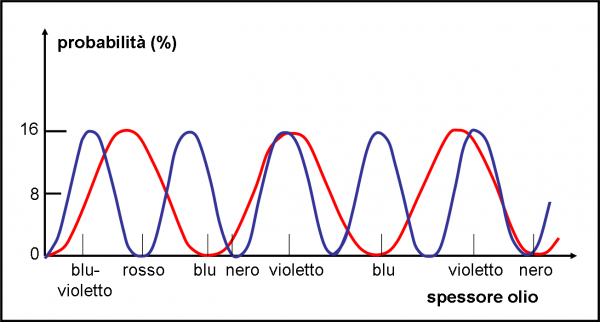
Se poi l’olio è versato sopra uno strato di acqua in movimento, ci dobbiamo aspettare che esso continui a variare localmente il suo spessore, comportando una continua variazione delle bande colorate. Figuriamoci, poi, cosa può succedere se quella che arriva è la luce solare, che contiene tutte le frequenze dell’ottico. Una meraviglia iridescente. Beh… l’aggettivo è scelto bene, dato che il fenomeno si chiama proprio iridescenza.

Avete capito benissimo che questo tipo di risultato potremmo spiegarlo benissimo considerando concetti come lunghezza d'onda, indice di rifrazione, dispersione della luce, cammino ottico, interferenza, e molte altre cose che sono di dominio (quasi) pubblico. Tuttavia, lo scopo della QED è proprio quello di descrivere tutto ciò che la fisica ha già dimostrato, basandosi sul calcolo delle probabilità. Solo così si possono “risolvere” problemi ben più generali e del tutto inaccessibili alla fisica classica.

A questo punto, abbiamo in mano lo strumento per il calcolo della probabilità finale di una certo evento. Per convincerci ancora di più della sua validità, applicheremo le nostre frecce e la loro combinazione ad altri fenomeni, come l’andamento rettilineo della luce, l’uguaglianza degli angoli di incidenza e riflessione, la capacità di concentrare la luce da parte di una lente, e tutto ciò che conosciamo attorno alla luce.

Ricapitoliamo ancora

Cosa abbiamo imparato fino ad adesso? Riassumiamo brevemente i concetti fondamentali. Innanzitutto abbiamo stabilito che la luce viene trasportata da particelle. La prova? Decisiva! Quando la luce di un solo colore (monocromatica) colpisce un rivelatore, si “sentono” nettamente i fotoni che la colpiscono. Inoltre, diminuendo la luminosità, ciò che si ottiene è la riduzione dei segnali che arrivano, ma la loro singola “intensità” non cambia.

Abbiamo poi stabilito, con non poco imbarazzo, che se la luce colpisce una superficie di vetro, alcuni fotoni vengono rimandati indietro, mentre altri (la maggioranza) proseguono all’interno del vetro. Comunque si cerchi di spiegare questo fatto non si riesce a capire perché qualche fotone scelga di rimbalzare e altri no. Soprattutto, non si riesce a stabilire chi di loro prenda una o l’altra decisione.

Se si aggiunge una seconda superficie riflettente, a breve distanza dalla prima, le cose diventano ancora più misteriose. Il numero totale di fotoni che subiscono una riflessione, o sulla prima o sulla seconda, invece di essere il doppio di quelli osservati con una sola superficie possono variare da zero fino a un valore massimo, superiore a ciò che ci si poteva aspettare. Sembra proprio che i fotoni che rimbalzano sulla prima superficie debbano attendere cosa facciano quelli sulla seconda per prendere una decisione. Assurdo, veramente assurdo. Malgrado una situazione di totale incomprensione, siamo riusciti ad affrontare e a descrivere il fenomeno considerando solo la probabilità di rimbalzare dei fotoni e, addirittura, di calcolare il risultato finale con due o più superfici. Ci si è riusciti attraverso delle semplici frecce e un ottimo cronometro ultra rapido. Ovviamente, si sono dovute seguire alcune regole molto precise:

1) La probabilità che accada un evento è data dal quadrato della lunghezza di una freccia che abbiamo chiamato ampiezza di probabilità.

2) Per calcolare la probabilità finale di un evento che ammette più vie alternative, basta disegnare un’ampiezza di probabilità per ogni alternativa (ogni “scelta” ?) e combinarle insieme secondo lo stesso metodo che ci permette di sommare i vettori.

Non dimentichiamo, però, che è necessario anche usare un cronometro che sappia scandire il movimento dei fotoni per determinare la direzione delle frecce. Un cronometro che gira in modo diverso a seconda del codice-colore del fotone. Più lentamente per il rosso e più velocemente per il blu.

Applicheremo, adesso, queste semplici regole ai principali fenomeni naturali che vedono la luce come protagonista. Lo faremo per i più comuni e conosciuti, ma Feynman ci assicura (e non possiamo fare altro che crederci) che il successo è garantito anche per fenomeni molto più complicati, come la diffrazione e anche “peggio”.

Uno specchio tuttofare

Iniziamo proprio con il fenomeno che ci è servito per introdurre le regole enunciate precedentemente, ossia la riflessione della luce. In poche parole, vogliamo descrivere come la luce si riflette su una superficie e perché  l’angolo di incidenza è uguale all’angolo di riflessione.

Ricordiamo brevemente cosa ci dice l’ottica geometrica “normale” e come si rappresenta la riflessione. Si considera una sorgente di luce S, uno specchio e un rivelatore R. Si traccia un bel raggio di luce che arriva sullo specchio in un certo punto M (non è un punto qualsiasi!), si calcola l’angolo tra la superficie e il raggio (o il suo complementare) e lo si riporta tale e quale dall’altra parte del punto. Il nuovo raggio finisce, ovviamente, sul rivelatore R. Lo vediamo nella Fig.14. Quante volte abbiamo disegnato questo semplice e logicissimo schema?

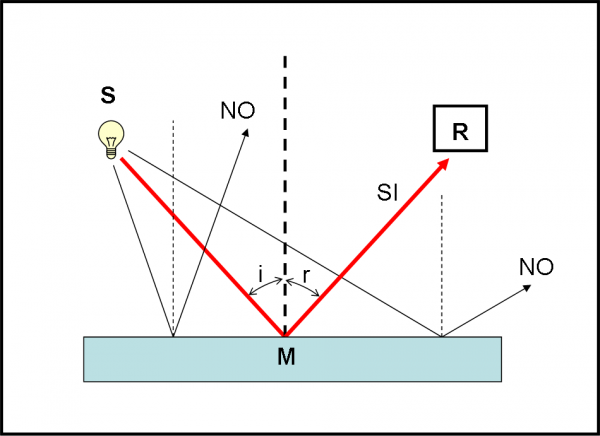
Ebbene, cerchiamo di cambiare un po’ il nostro modo di pensare, come potrebbe fare Alice.

Per quale motivo abbiamo disegnato un solo raggio che lascia la sorgente S? In fondo, sappiamo benissimo che i fotoni possono andare in qualsiasi direzione. Perché scegliere solo la direzione che ci fa comodo? Perché trascurare tutte le altre? Un po’ alla volta questo modo di ragionare così “normale” comincia ad apparirci illogico. E’ come se avessimo fatto una scelta arbitraria che favorisce certi fotoni solo perché sappiamo il risultato finale, senza curarci della realtà dei fatti.

D’altra parte i rivelatori ci hanno dimostrato senza ombra di dubbio che i fotoni sono corpuscoli che sembrano viaggiare in linea retta e che quando arrivano sul rivelatore ci informano attraverso il loro “tac”. Dobbiamo trattarli così e analogamente dobbiamo accettare che essi vadano in ogni direzione. Ciò vuole anche dire che i fotoni che partono da una sorgente possono toccare qualsiasi punto dello specchio e non solo il punto M che ci mostra la riflessione di un SOLO raggio e che si trova per ovvi motivi geometrici proprio alla stessa distanza da S e da R.

Potremmo concludere che sì, è vero che vi sono molti altri raggi, ma nessuno di essi, riflettendosi, può raggiungere il rivelatore R e, di conseguenza, li possiamo tranquillamente trascurare e concludere che vale la pena disegnare solo quello che serve. In altre parole, potremmo concludere che i fotoni che colpiscono lo specchio vicino ai suoi estremi (più vicini a S e a R) non abbiano niente a che fare con quelli che hanno la possibilità di raggiungere R, come sembra indicare perfettamente la Fig. 14.

Se, però, questo ragionamento comincia a sembrarci troppo semplicistico, come se cercasse di mettere la polvere sotto al tappeto, vuol dire che abbiamo buone possibilità di seguire Alice nel suo mondo assurdo. La MQ ci ha ormai segnato e il dubbio che si stia sbagliando a vedere le cose in modo troppo “normale” diventa sempre più forte.

Serviamoci ancora della stessa Fig. 14, ma la ridisegniamo come Fig. 15. Non cambia la situazione, ma cambia il modo di affrontare il problema. La sorgente S “spara” un fotone alla volta, dello stesso codice, per esempio il codice “rosso”. Qualsiasi traiettoria dei fotoni che partono da S è possibile e nessuna va trascurata. In R mettiamo il solito rivelatore di fotoni. Cosa dobbiamo fare per seguire gli insegnamenti della QED? Dobbiamo calcolare la probabilità di arrivare su R di qualsiasi fotone, dopo che ha toccato lo specchio. Nessuno è favorito a priori e lavoriamo in modo del tutto imparziale, come dovrebbe fare qualsiasi VERO arbitro di una partita di calcio.

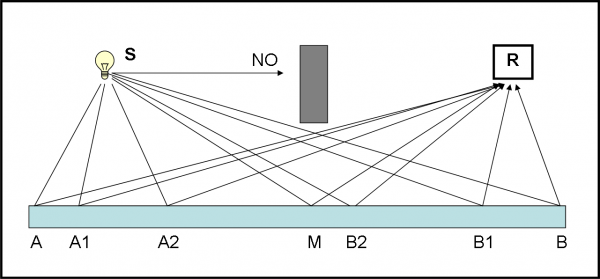
Per evitare che qualche fotone prenda una scorciatoia (i fotoni ne sanno una più del diavolo), mettiamo uno schermo tra sorgente e rivelatore, in modo che i “furbi” che volessero prendere la direzione diretta da S a R vengano bloccati. Liberata la mente da riflessioni troppo comuni e razionali, immergiamoci completamente in quello che ci ha insegnato, finora, la QED. Applichiamo, quindi, le regole che conosciamo.

La probabilità che un certo evento si verifichi è il quadrato della freccia finale che si ottiene combinando assieme tutte le frecce delle varie possibilità che possono portare all’evento finale. Non spaventatevi… è proprio quello che abbiamo fatto usando la lamina di vetro. In quel caso vi erano solo due possibilità per raggiungere R1: o attraverso la riflessione sulla prima superficie o sulla seconda. Ricordatevi che per calcolare la probabilità finale abbiamo proprio combinato due frecce relative a queste due possibilità di azione.

Nel “nuovo” esperimento le cose si complicano non poco (apparentemente), dato che vi sono milioni o miliardi, o il numero che volete, di possibilità per far giungere la luce di S in R. Il tragitto del fotone, infatti, non è assolutamente legato a ciò che noi vogliamo dimostrare (angolo di incidenza uguale all’angolo di riflessione), ma segue tutte le possibili vie che ha a disposizione. Non possiamo certo limitarne le possibilità sapendo qual è il risultato. Vale proprio il contrario: considerando tutte le vie di manovra dobbiamo dimostrare che l’angolo di incidenza è uguale a quello di riflessione. Il discorso è completamente diverso!

Accettiamo, quindi, stringendo i denti e annullando tanti concetti imparati a scuola, che i fotoni possano fare tutti i percorsi possibili, colpendo lo specchio in qualsiasi suo punto e poi giungere, comunque, in R, “fregandosene” bellamente delle regole dettate dal buon senso. Quanto detto è rappresentato nella Fig. 15, dove abbiamo disegnato solo qualche percorso possibile. Non sentiamoci “pazzi” perché stiamo accettando un qualcosa che sappiamo che non “dovrebbe” essere logico. Affidiamoci solo e soltanto alle probabilità.

Per essere ancora più chiari, eseguiamo una semplificazione che non cambia certamente il risultato (lo abbiamo imparato studiando la definizione di limite e cose del genere).  Consideriamo il nostro specchio sotto forma di striscia e dividiamolo in tanti tasselli quadrati tutti uguali tra loro. Accettiamo, inoltre, che per tutti i punti del tassello la luce si comporti in un solo modo, come descritto in Fig. 16. Spieghiamoci meglio. Sappiamo benissimo che ogni punto dello specchio colpito dalla luce dà luogo a una certa freccia probabilistica, ossia dà luogo a un comportamento diverso dai punti adiacenti. Per trattare, però, milioni e milioni di punti, con comportamenti diversi,  dovremmo fare uso, quantomeno, degli integrali. Molto meglio, dividere lo specchio in piccoli tasselli di dimensioni “finite” e assumere che ognuno di essi dia luogo a un certo comportamento.

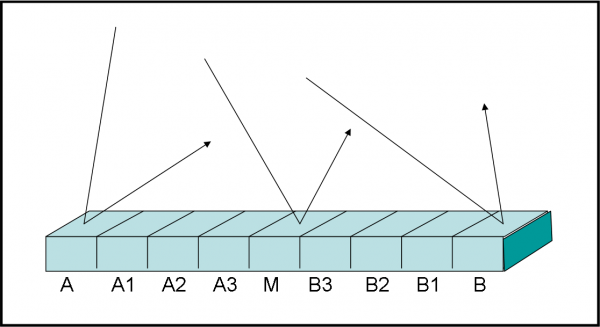
Il risultato che otteniamo è soltanto più approssimato, ma non cambia più di tanto. Sicuramente è più che sufficiente per i nostri scopi. Niente ci vieta, inoltre, di migliorare la rappresentazione, riducendo sempre più le dimensioni dei singoli tasselli, facendoli un po’ alla volta tendere verso dimensioni nulle (e qui saltano fuori i concetti di limite e via dicendo…). Non lo faremo, proprio perché non vogliamo introdurre  formule molto “cattive”, ma perfette, che sono il punto di forza della QED. Accontentiamoci e non ce ne pentiremo!

Fatte queste premesse, possiamo concludere che ogni tassello è caratterizzato da un’unica freccia che ha una certa lunghezza e una certa direzione. Cominciamo con la lunghezza. Nuovamente non facciamo il solito errore a cui ci porta la logica comune. La lunghezza di una freccia indica, in pratica, la probabilità che ha un fotone che arriva su di esso di rimbalzare esattamente sul rivelatore R. Verrebbe da dire che la probabilità è sicuramente massima per il tassello (chiamiamolo pure punto) che sta a metà dello specchio, ossia in M. Ne dovrebbe seguire che la lunghezza di questa freccia debba essere la massima.

Ovviamente, commetteremmo un errore, dato che partiremmo condizionati dal risultato che tutti conoscono nell’esperienza comune. Analogamente, saremmo portati a disegnare una lunghezza piccolissima per le frecce di A e B. No, no… dobbiamo seguire le regole imparate nell’articolo precedente. Un fotone che arriva in un qualsiasi punto ha “praticamente” sempre la stessa probabilità di dirigersi da qualsiasi parte esso voglia. Attenzione: in realtà una leggerissima differenza esiste, ma è talmente insignificante che possiamo trascurarla (parola di Feynman e delle sue formule).

Possiamo perciò considerare costante la lunghezza della freccia relativa a ogni punto (o -meglio- tassello). Il che vuol dire che anche il suo quadrato rimane costante e quindi anche la probabilità del singolo evento. Questo concetto è veramente fondamentale per tutta la MQ: la probabilità relativa a una qualsiasi "scelta" fatta dal fotone è sempre la stessa. Il fotone ha  la stessa probabilità di raggiungere qualsiasi punto ( e anche -come vedremo- di seguire  qualsiasi traiettoria). Tutta la MQ si fonda su questo semplicissimo principio: la realtà si descrive così. Punto e a capo!

La stessa cosa, però, non succede certo per la direzione della freccia. La direzione dipende da quanti giri ha fatto la lancetta del cronometro tra la partenza del fotone da S e il suo arrivo in R. Senza alcun dubbio, i percorsi SR sono ben diversi a seconda del punto in cui il fotone tocca lo specchio. Maggiore o minore è il percorso e maggiore o minore è l’angolo della direzione finale della lancetta rispetto a una certa direzione di riferimento. Ricordiamoci che tutti i fotoni hanno lo stesso codice e quindi il cronometro gira alla stessa velocità per tutti.

Consideriamo la Fig. 17. Due fotoni seguono due percorsi differenti. Il primo tocca lo specchio in A e il secondo in M.  Entrambi devono poi arrivare fino a R. Beh, non c’è QED che tenga: il percorso SAR è sicuramente più lungo di SMR. Percorso più lungo vuole dire posizione diversa della lancetta del cronometro che ha dovuto compiere una frazione di giro in più (o magari anche molti giri completi più una frazione di giro). In altre parole, c'è voluto  più tempo per descrivere il percorso SAR che non quello SMR. La velocità del cronometro è sempre la stessa, ma il percorso ha lunghezza differente.

Introduciamo un nuovo tipo di figura decisamente comoda e comprensibile. Per ogni punto dello specchio colpito, il percorso SR ha lunghezza diversa e di conseguenza varia il “tempo” (giri e frazioni di giro) misurato dal cronometro dalla partenza all’arrivo del fotone corrispondente (la velocità è la stessa) . La Fig. 18a rappresenta schematicamente i percorsi eseguiti dai vari fotoni che abbiamo considerato (forse sarebbe meglio dire il percorso scelto da ogni fotone per arrivare in R), mentre la Fig. 18b descrive proprio la relazione tra posizione del punto colpito e tempo di percorrenza del tragitto relativo. In poche parole, inseriamo come ascissa la distanza di ogni punto dello specchio rispetto ad A (per esempio) e in ordinata il “tempo” impiegato dal fotone che ha colpito lo specchio in quel punto, per andare da S a R.

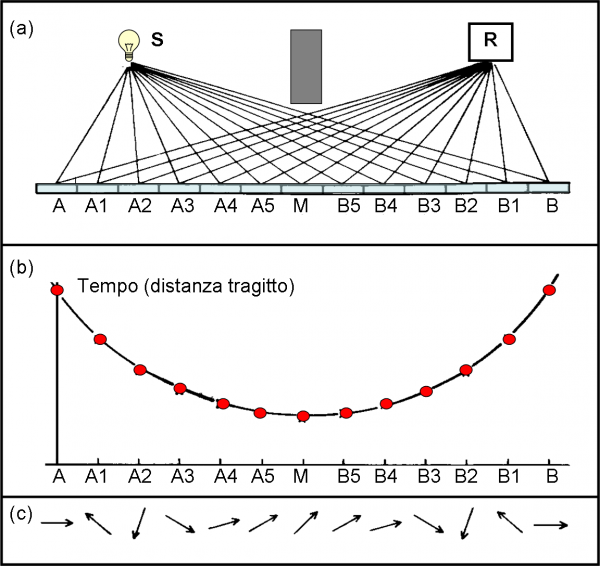
Otteniamo una specie di parabola (unendo i punti vediamo proprio una parabola disegnata a “scatti”, che sarebbe sempre più raffinata aumentando i punti). All’inizio (in A) il tempo è molto lungo. A mano a mano che il punto si avvicina a M il tempo diminuisce. Superato M il tempo ricomincia ad aumentare fino ad arrivare in B, dove è ovviamente uguale a quello di A per come è stato rappresentato lo specchio, la sorgente e il rivelatore.

Possiamo anche vedere (e questo fatto è veramente importante!) che spostandoci anche di poco rispetto ad A il tempo cambia sensibilmente, mentre avvicinandosi a M la variazione decresce sempre di più. L’andamento si ripete andando da M verso B. Conoscere bene le caratteristiche della funzione “parabola”, o quello che è, può servire moltissimo se volessimo scrivere le formule relative (ecco perché è importante lo studio delle funzioni…).

Quanto detto per i tempi si trasferisce immediatamente alla direzione della lancetta del cronometro. Vicini ad A la differenza di direzione della  freccia varia notevolmente da punto a punto, mentre vicini a M la lancetta cambia di poco la direzione, che si mantiene pressoché costante. Poi, ricomincia a variare sempre di più, giungendo in B con la stessa direzione di A, dato che il percorso SAR è uguale, per costruzione, a SBR. Possiamo, perciò disegnare al fondo della Fig. 18 (Fig. 18c) le frecce calcolate punto per punto, con lunghezza costante e direzione più o meno variabile a seconda del tempo impiegato o –meglio ancora- dello spostamento della lancetta.

Ovviamente, abbiamo scelto la direzione della freccia di A qualsiasi (poco importa). Quelle successive hanno però una stretta correlazione con la prima, seguendo quanto detto precedentemente.

Non ci rimane, adesso, che “sommare” tutte le frecce, ossia combinarle con le regole imparate la volta scorsa. Prima di farlo, devo fare un'importante precisazione. Nell’esperimento della lastra di vetro dell’articolo precedente, avevamo invertito il verso della prima freccia e non quello della successiva. La regola non vale più in questo caso, dato che la riflessione avviene nello stesso modo per tutti i percorsi. In altre parole, la freccia gira di 180° o non gira affatto, a seconda del materiale in cui avviene la riflessione. Ricordiamoci, infatti, che stiamo sempre usando la semplificazione che dice di considerare una riflessione come fenomeno che coinvolge solo la superficie. In realtà non è così, ma per essere più esatti dovremmo sapere fare interagire fotoni con materia. E questo lo faremo solo più in là. Accettiamo, quindi, queste rotazioni di mezzo giro che a volte si compiono e a volte no, come un piccolo atto di fede che risolveremo in seguito. Nel caso in esame, abbiamo la riflessione su vetro, provenendo da aria, per tutti percorsi effettuati dalla luce. Non vi è quindi bisogno di introdurre capovolgimenti di verso della freccia.

Un bel "lento" o un bel "tango"?

Torniamo al caso in oggetto e combiniamo le frecce mantenendo per tutte il verso della lancetta. Il risultato è oltremodo simpatico e intrigante, come mostrato in Fig. 19.

Non solo è simpatico, ma anche descrivibile molto bene. Le prime frecce, vicine ad A, cambiano drasticamente direzione e ciò vuol dire che in pratica la loro combinazione fa tanto fumo e poco arrosto: la freccia finale, relativa a loro, rimane piccola. Ricordate l’analogia con la “danza”? Ebbene, vicini ad A è come se ballassimo un lento. Ogni passo avviene in una direzione completamente diversa da quella precedente, ma alla fine si rimane sempre sulla stessa “mattonella”. Le cose invece cambiano drasticamente avvicinandosi a M. I vari passi sono, adesso, tutti diretti verso una direzione quasi costante. La combinazione di queste frecce, così simili, porta a uno spostamento non certo trascurabile. Poi, andando verso B le frecce tornano ad essere caotiche e “inconcludenti”. Ne segue che la freccia finale, dipende essenzialmente dalla direzione, quasi costante, delle frecce vicine al punto medio M. Vi prego di non prendere la figura come una disegno precisissimo: l’ho tracciata un po’ a occhio e con ovvie approssimazioni. Ricordiamoci, comunque, che la lunghezza delle singole frecce deve essere sempre uguale.

Non perdiamo di vista lo scopo di questo bel gioco di frecce e lancette. Ciò che volevamo trovare era proprio la direzione e la lunghezza della freccia finale, il cui quadrato indica proprio la probabilità di avere una riflessione sullo specchio e raggiungere R. Ci siamo riusciti e abbiamo visto che questa probabilità è alta (dipende dalla lunghezza della freccia finale) ed è essenzialmente legata alla somiglianza della direzione delle frecce vicine al punto di mezzo dello specchio. Attenzione: la direzione della freccia finale, in sé, conta poco; quello che conta è la lunghezza della freccia finale o, se preferite, dalla costanza della direzione delle frecce che permette di sommare veramente la loro lunghezza. In altre parole, ciò dimostra che per raggiungere il rivelatore M è molto meglio che il fotoni tocchino lo specchio vicino al punto di mezzo, dove l’angolo di incidenza è quasi uguale all’angolo di riflessione e il “tempo” impiegato è  quello minimo. Questa è la zona dello specchio che dà il massimo contributo alla probabilità totale  che l'evento (riflessione) avvenga.

Se guardiamo bene la Fig. 19, notiamo che il risultato finale non sarebbe cambiato di molto se avessimo eliminato il contributo delle prime frecce a sinistra e delle ultime a destra. In parole povere, chi comanda sono le frecce vicine a M. Questa conclusione può approssimarsi alla visione del mondo normale, dove si dice che i fotoni che partono da S, e si riflettono sullo specchio raggiungendo R, lo fanno colpendo lo specchio nella parte mediana, ossia con un angolo di incidenza uguale all’angolo di riflessione, impiegando il minor tempo possibile per andare da S a R.

Possiamo anche fare un’ulteriore considerazione: le probabilità dei fotoni che colpiscono lo specchio vicini ad A e a B, e poi raggiungono R, sono del tutto simili a quelle della parte mediana dello specchio, ma esse sono talmente “variabili” che le loro probabilità praticamente si annullano a vicenda , quando vengono combinate. Troppa agitazione porta, veramente, a poco o niente. La calma e la costanza delle frecce mediane, invece, premia, dato che le frecce si sommano dando luogo a una probabilità finale decisamente grande.

Solo dopo aver fatto questa riflessione possiamo dire di  escludere tranquillamente le parti laterali dello specchio e ottenere lo stesso risultato! Inoltre, ragionando in termini di probabilità, il fatto che la probabilità di un evento composto da due eventi, possa essere minore o maggiore della probabilità di un singolo evento, diventa un risultato del tutto “normale”. L’esperimento della lastra di vetro della volta scorsa perde molto della sua assurdità, che sembrava mostrare che i primi fotoni decidessero qualcosa solo dopo che i secondi avevano fatto la loro scelta? Sembrerebbe di sì, dato che l’annullamento o la somma delle probabilità dipende solo dalla direzione delle frecce.

No, no, non cerchiamo di riportare Alice nel nostro mondo. Resta sempre il problema di partenza. Perché un fotone decide di andare in una direzione e non in un’altra, di attraversare o non attraversare il vetro? La QED ci permette di ottenere il risultato finale con estrema esattezza, ma non riesce assolutamente a spiegare il perché! Un po’ alla volta, iniziamo a capire che le particelle non possono sempre essere trattate come tali e che a ognuna di esse bisogna collegare o sostituire (o quello che volete) la probabilità e non la certezza di un fenomeno di fisica classica.

Insomma, abbiamo capito benissimo che tracciare la solita retta che parte da S, arriva in M e giunge, infine, in R è solo e soltanto un’approssimazione di un comportamento più complesso descritto dalla QED! Sembrerebbe un’inutile perdita di tempo, dato che si ottiene lo stesso risultato della fisica classica, ma studiando meglio la situazione, vedremo che è in realtà molto più corretto (e utile) accettare che tutta la superficie dello specchio concorre al fenomeno della riflessione. Troppo semplice e parziale limitarci a una sola direzione privilegiata. Entrando nella logica illogica della MQ, cominciano veramente ad apparire troppo limitativi gli espedienti usati nella fisica classica per spiegare certi fenomeni all’apparenza molto, anzi troppo, ovvi.

Fermiamoci a riflettere 

Un consiglio… mentre andiamo avanti con questa descrizione essenzialmente grafica e un po’ empirica, cerchiamo di confrontare certi concetti (espressi in modo diverso) con quelli che avevamo “toccato” spiegando l’esperimento della doppia fenditura. Vi renderete conto che stiamo dicendo le stesse identiche cose… Uno sforzo non trascurabile, senza far uso di formule esatte, ma molto stimolante e fondamentale per capire quanto sia incomprensibile la MQ e quanto sia corretta e precisa nel descrivere la Natura. Invece di sprecare tempo e capacità mentale a immaginarsi stringhe, universi paralleli, buchi neri e buchi bianchi che si accavallano, tempi che rallentano, accelerano e/o invertono la loro freccia, dedichiamoci PRIMA a capire le basi della MQ, ormai perfettamente descrivibili con esempi semplicissimi. Senza di esse qualsiasi sproloquio sulle ultime teorie dell’Universo diventa un falso Picasso…

Non odiatemi per la ripetizione di questo concetto che sembra negare la fantasia e l’immaginazione. Lo faccio sia per voi che per me stesso. La fantasia è meravigliosa solo se poggia su una conoscenza completa di ciò che vogliamo estrapolare e inventare. Altrimenti è solo e soltanto un gesto di arroganza e di superficialità…

Prima di proseguire, vorrei scrivere qualche considerazione aggiuntiva, sperando che chiarisca meglio certe idee e non porti invece a incomprensioni.

Ho detto che il fotone è una particella, basandomi solo e soltanto sul fatto che quando colpisce un  rivelatore dà un chiaro segnale di arrivo. Non solo, però... anche perché diminuendo l’intensità della luce ho notato che il segnale di arrivo resta sempre uguale:  diminuisce solo il numero di segnali nell’unità di tempo.

Con queste prove in mano NON posso che considerare la luce come un’informazione trasportata da una particella.

Tuttavia, uno specchio piano parzialmente riflettente (non c’interessa assolutamente sapere, per adesso, PERCHE’ e nemmeno COME si ottenga uno specchio parzialmente riflettente), ci dimostra che le supposte particelle sembrano decidere dove andare in modo del tutto casuale senza alcuna ragione legata alla fisica che conosciamo. Contando i fotoni che arrivano sul rivelatore possiamo valutare la probabilità che succeda questo evento, ma non chi e perché ha deciso di scegliere quella strada.

Ho  una sola strada davanti: accettare di non capire e cercare di descrivere e calcolare la probabilità, l’unica cosa che riesco a osservare.

Vi sono due modi per descrivere, che però coincidono praticamente, ma non concettualmente. A questo punto, forse, vi ho creato confusione.

La prima descrizione dice che se invio una serie di fotoni verso lo specchio, ognuno segue una sua certa strada (che però non so da chi o da cosa sia stata decisa) per poi giungere sul rivelatore. Cosa ho fatto in pratica? Ho preso molti fotoni che hanno già deciso la traiettoria e ho calcolato la probabilità che qualcuno raggiunga il rivelatore. In questo contesto, la freccia di probabilità che abbiamo costruito può tranquillamente associarsi a ogni singolo fotone o -meglio- alla traiettoria che ha SCELTO. Abbiamo visto che la probabilità finale è dovuta, soprattutto, a fotoni che colpiscono la parte centrale dello specchio, dove le traiettorie sono più corte e più rapide. Cosa succede agli altri fotoni laterali? Malgrado abbiano tutte le possibilità di arrivare sul bersaglio, essi litigano con i vicini di casa e si ANNULLANO. In realtà non si annullano loro, ma le probabilità a loro associate.

Ho scelto questo modo di parlare per rendere meno indolore il passaggio alle assurdità logiche della MQ. Ho potuto farlo, dato che l’applicazione delle regole di combinazione non cambiava il risultato e il concetto in sé. Tuttavia, prima o poi ci saremmo scontrati con una visione completamente differente anche se apparentemente simile.

Ragioniamo, allora, in altro modo. Per far questo, però, dobbiamo dimenticarci che il fotone è una particella, malgrado le sue caratteristiche. Ma non dobbiamo nemmeno pensarla come un’onda “marina”, se no andremmo troppo avanti e la confusione sarebbe ancora maggiore. Consideriamola pure particella, ma accettiamo che non vi è nessuna speranza di sapere la direzione che ha scelto lasciando la sorgente. Essa quindi si scompone, in pratica, in milioni e milioni di possibili traiettorie, tutte altrettanto valide, che portano con sé una certa probabilità (uguale per tutte) di arrivare sul bersaglio. Dato che sono assimilabili a fotoni diversi posso trattare la combinazione delle loro probabilità nello stesso modo precedente. In realtà, però, siamo un passo prima, dato che non vi è ancora nessun fotone che ha preso una decisione. Stiamo perciò calcolando la probabilità che ha un singolo fotone di dare luogo a una certa traiettoria finale. Tutte queste traiettorie virtuali (possiamo chiamarle così)  si comportano come fotoni reali singoli, ma non lo sono ancora. Solo dopo aver calcolato la combinazione delle singole probabilità potremo anche stabilire la traiettoria più probabile del fotone che diventerà uno e uno solo.

Se ci pensate bene, le due visioni sono identiche, perché portano allo stesso risultato, ma, mentre la prima ci fa lavorare con un certo legame con la realtà (e per adesso non comporta problemi), la seconda ci immerge subito nella MQ, ossia ci fa descrivere una particella come un insieme di probabilità, di cui possiamo SOLO calcolare il risultato finale, ma non interpretare fisicamente.

Nel secondo caso, quando le frecce si annullano a vicenda non si sono annullati dei fotoni, ma si sono annullate le probabilità di quelle possibili traiettorie.

Spero proprio che riusciate a vedere la differenza poco pratica ma molto concettuale.

Il vero impatto con l’assurdo avverrà quando arriveremo alla doppia fenditura (non per altro è stata considerata come esperimento magico e fondamentale). Per adesso possiamo continuare a considerare un fascio di fotoni che arrivano in diverse posizioni o un solo fotone con una serie enorme di possibili  traiettorie. Teniamo bene a mente, però, il concetto di fondo che già ci introduce il carattere ondulatorio del fotone…

Fatemi riassumere velocemente quanto abbiamo fatto finora.

Mandando luce e ricevendola su un rivelatore abbiamo scoperto che essa è trasportata da particelle (si sente un “tic” e se diminuisco l’intensità della luce non diminuisco il "tic", ma si riduce solo il numero dei “tic”).

Proviamo a mettere uno specchio parzialmente riflettente tra la sorgente e il rivelatore. Ci accorgiamo che le particelle (fotoni) pur essendo tutte uguali si comportano in modo diverso: la maggior parte attraversa lo specchio e una piccola parte torna indietro. Anche lo specchio non può aiutarci. Non abbiamo nessuna spiegazione fisica per capire questa scelta fatta dal singolo fotone e alziamo bandiera bianca.

L’unica cosa che possiamo fare è studiare la situazione attraverso la probabilità che dimostra il fotone di arrivare sul rivelatore o di proseguire. Per far questo introduciamo una freccia che indica l’ampiezza di probabilità e misuriamo il tempo impiegato per effettuare il percorso dalla sorgente al rivelatore, attraverso un cronometro. La direzione della lancetta di quest’ultimo nel momento di arrivo, ci indica la direzione della freccia.

Proviamo a vedere se questa strategia operativa funziona per una doppia riflessione su una lastra di vetro. Sembra proprio di sì e allora decidiamo di usarla per qualsiasi evento che vede la luce protagonista.

Non sapendo assolutamente dove si dirige il fotone dopo aver lasciato la sorgente, consideriamo tutte le possibili traiettorie che può compiere per arrivare sul rivelatore. Ognuna di esse ha, per definizione la stessa ampiezza di probabilità. Tuttavia, le traiettorie vengono percorse in tempi diversi e quindi le frecce hanno direzioni diverse.

Possiamo facilmente combinare tutte queste frecce e calcolare la probabilità finale del fotone di arrivare al rivelatore. Non basta, però. Riusciamo anche a vedere quali percorsi contribuiscono di più al successo dell’impresa. Dato che le frecce relative a percorsi diversi da quelli più “costruttivi” non danno contributo significativo, possiamo concludere che le traiettorie più costruttive sono quelle scelte preferenzialmente dal fotone.

Questo approccio non solo spiega le osservazioni, ma indica anche che le conclusioni della fisica classica sono solo approssimazioni di quanto realmente succede lavorando con le probabilità.

Le varie traiettorie possibili seguite da un fotone assumono un valore del tutto indipendente una dall'altra e possiamo considerarle come percorse da particelle virtuali, dato che non abbiamo modo di sapere dove realmente si sia diretto il fotone. Esse hanno le loro probabilità che si combinano dandoci la probabilità finale dell'evento e dicendoci quale  percorso è stato probabilmente seguito dal fotone, che riusciamo a rivelare solo alla fine e non durante il viaggio. Guai a cercare di vederlo durante il tragitto: improvvisamente tutte le altre traiettorie scomparirebbero così come tutte le particelle virtuali! ma, questa è un'altra storia (almeno per adesso).

Divertiamoci un po’ con il nostro specchio e le sue frecce vagabonde. Impareremo molte cose interessanti. Molte altre le intuiremo soltanto non potendo scendere troppo nei dettagli. Abbastanza, però, per far venire voglia a qualcuno di procedere da solo.

A che servono i bordi dello specchio?

Innanzitutto, vogliamo dimostrare, in modo assoluto, quanto abbiamo detto un po’ vagamente, ossia che le parti laterali dello specchio non danno praticamente contributo alla riflessione della luce, dato che le frecce si eliminano una con’altra. Non ce ne sarebbe bisogno, dato che è già abbastanza intuitivo, ma prendiamolo come un “gioco” distensivo in vista di qualcosa di un po’ più impegnativo.

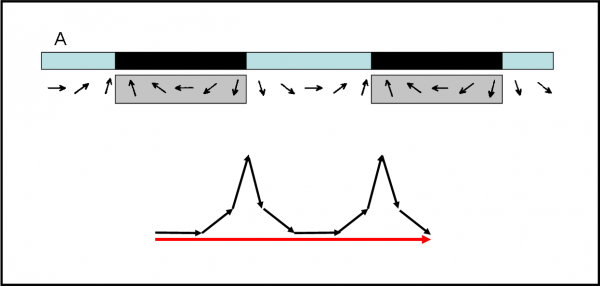
Per giungere a una conclusione veramente efficace, eliminiamo letteralmente (coprendolo con un cartone) tutto lo specchio tranne una zona molto vicina ad A (Fig. 20).

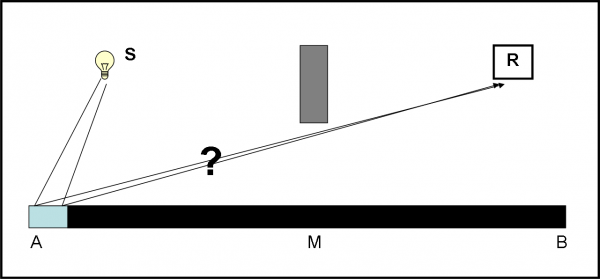
Per essere ancora più precisi diciamo che teniamo quella parte di specchio dove il tempo di arrivo su R varia di molto ma pressoché linearmente con la distanza da A (Fig. 18b). Non ci tragga in inganno la Fig. 18a. La freccia è indicata solo in alcuni punti. Tra uno e l’altro la direzione varia molto, quando si è vicini ad A. Tuttavia, non pensiamo che tra SAR e  SA1R, ad esempio, la freccia abbia solo fatto una frazione di giro. Il cronometro è talmente veloce che ha probabilmente fatto molti giri più una frazione… Basta un piccolo spazio in più da percorrere e la freccia gira molte volte. Vicini ad M, invece, la freccia non è riuscita proprio a girare, dato che i percorsi sono veramente simili tra loro. Per vedere bene la reale situazione bisogna indicare molti più punti lungo lo specchio.

Fatte queste dovute precisazioni, vediamo in dettaglio cosa capita se lasciamo scoperto solo un pezzetto di specchio vicino ad A. Questa volta, possiamo assumere che tra un punto e quello successivo la freccia abbia veramente girato di una frazione di giro in più. E lo ha anche fatto in modo abbastanza uniforme (ecco perché ho detto di rimanere nella zona in cui la parabola coincide praticamente con una retta).

Nella Fig. 21, i punti indicati stanno quindi in un intervallo molto piccolo di specchio, tutti compresi, per esempio, tra A e A1. Nella parte alta vediamo come variano le direzioni delle frecce. Come previsto, la differenza, da punto a punto, rimane, comunque, molto grande dato che il tempo tra partenza e arrivo cambia sempre abbastanza. Aumentando i punti e diminuendo la distanza fra loro è molto più facile, però, seguire come varia veramente la direzione della freccia. Sotto alla parte dello specchio usato, sono state disegnate le frecce relative.

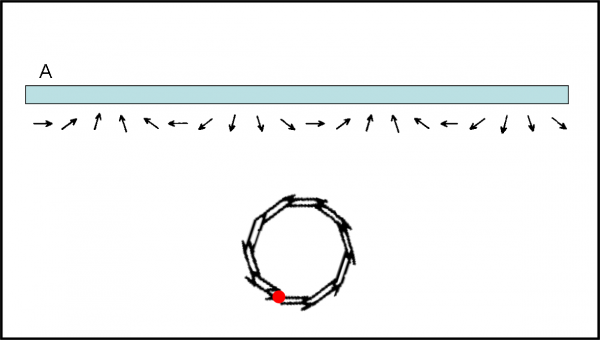
E’ immediato vedere che tra una e l’altra, lo spostamento angolare rimane quasi costante (il tempo -e, quindi, il percorso- varia linearmente). Diventa un gioco da bambini combinare le frecce tutte assieme secondo la ormai famosa regola, come fatto nella parte bassa della figura. Ci dobbiamo stupire se esse girano in tondo per due volte, tornando al punto di partenza? Direi proprio di no, c’era da aspettarselo! Questo simpatico girotondo di frecce cosa ci dice? Che la freccia finale, combinazione di tutte quelle del nostro pezzo di specchio, ha una lunghezza esattamente uguale a ZERO. In altre parole, la probabilità di avere una riflessione della luce in grado di raggiungere R è nulla. Potevamo eliminare questo pezzo di specchio e niente sarebbe cambiato.

Qualcuno mi dirà: “Che scoperta! Era veramente assurdo aspettarsi che la riflessione potesse arrivare in R attraverso uno specchietto posto sotto alla sorgente, con R molto più spostato verso destra. Bastava tracciare poche linee e l’ottica geometrica ce l’avrebbe detto subito”. In effetti, sembrerebbe proprio di aver perso un mucchio di tempo a far girare inutilmente una freccia la cui “somma” ha dato zero. Bastava limitarsi alla zona vicino a M e cercare la traiettoria di minore lunghezza  (quella che il fotone ha percorso in minor tempo) per dire che lì ci sarebbe stata la massima probabilità di riflessione.

Ecco che la logica “normale” cerca di riprendere il sopravvento e ci sta convincendo che non vi è nessun bisogno di parlare “solo” in termini di probabilità. E’ molto meglio tornare alla vecchia e sicura fisica classica e all’ottica geometrica.

Il gioco dei tre… cartoni

Datemi, però, un’altra possibilità, sempre con la parte di specchio che sembra del tutto inutile. Faccio una cosa abbastanza strana, ma molto, molto interessante. La “maschero” ancora di più, ma stando bene attento alle parti che copro con il cartone. La figura è sempre la Fig. 20, ma, questa volta, con alcune zone, del residuo di specchio, rese impossibilitate a riflettere. Vedo già il sorriso di qualcuno: “Povero illuso! Se tutto lo specchietto non era capace di riflettere la luce su R, come puoi pensare minimamente che riesca a farlo lo stesso specchietto mascherato in più parti. Se  tutto non ci riesce, non ci riesce, a maggior ragione, la sua metà o anche meno, anche se mascherata a strisce…”. Io rispondo soltanto: “Vogliamo provare?” e disegno la Fig. 22.

Sono stato, ovviamente, molto attento a quale parte nascondere e quale lasciare libera, ma alla fine ottengo la parte alta della Fig. 22. Coprendo alcune parti dello specchietto, sempre più piccolo, ho eliminato le frecce che corrispondono alle zone ora nascoste. Se queste sono coperte dal cartone, la probabilità di riflettere non può che essere zero: va bene dire assurdità, ma un pezzo di cartone non può riflettere nemmeno nella QED.

Non mi resta allora che prendere le frecce che mi rimangono e combinarle assieme, sempre secondo la celeberrima regola vettoriale. Il risultato è mostrato nella parte bassa della figura. Vi sembra una probabilità nulla? Assolutamente no, anzi è decisamente alta! Quello che uno specchietto messo nella posizione sbagliata non era riuscito a fare, lo fa, ora, coprendone qualche parte. Se non è assurdo questo… Eppure, non ho fatto altro che descrivere il funzionamento (probabilistico) di un reticolo a diffrazione. E dico poco… Tutto ciò solo e soltanto con quelle piccole frecce che sembravano non servire a niente.

Facciamo subito una constatazione che ci serve a “spiegare” anche l’esperimento della doppia riflessione. Nello specchio mascherato di Fig. 22 abbiamo eliminato, in pratica, solo le frecce che puntano verso sinistra e abbiamo tenuto quelle che puntano verso destra. Potevamo fare il viceversa e avremmo ottenuto lo stesso identico risultato. Si può quindi facilmente concludere che lo specchio perde le sue capacità, dando probabilità finale nulla, quando si combinano assieme le frecce che puntano a sinistra e quelle che puntano a destra. L’analogia con la doppia riflessione è perfetta. Se le frecce delle due riflessioni vanno nello stesso verso la probabilità finale si amplifica, ma se vanno in verso opposto la probabilità si annulla del tutto.

Toniamo al nostro personale reticolo di diffrazione e vediamo quale altra cosa sa fare. Innanzitutto dobbiamo ammettere che quello che abbiamo appena descritto è stato costruito su misura per la luce rossa. Se usassimo la luce blu (per la quale il cronometro gira più velocemente) dovremmo modificare le zone di specchio libere di agire. In particolare, dovremmo diminuire la distanza tra le strisce riflettenti, dato che il ciclo probabilistico del blu è più rapido.

Tuttavia, potremmo anche usare il reticolo del rosso, spostando il rivelatore R. La geometria cambia e così pure i percorsi che deve fare la luce. Troveremmo che, per una certa posizione, il reticolo rosso funziona perfettamente anche per il blu, come mostra la Fig. 23.

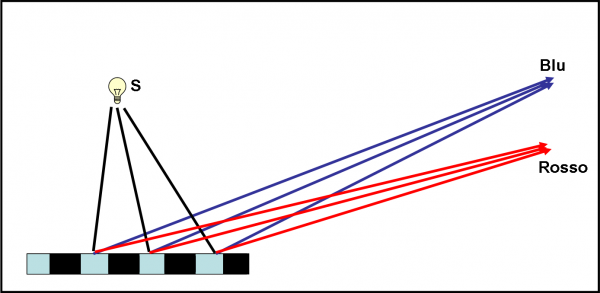
Analogamente, potremmo anche inviare luce bianca, quella solare, e vedremmo che spostando verso l’alto il rivelatore scorgeremmo prima la luce arancione, poi quella gialla per concludere con la verde e la blu. Insomma, proprio i colori dell’arcobaleno. Capite immediatamente che invece di spostare il rivelatore, potremmo benissimo costruire un rivelatore in grado di ricevere tutti i “codici” luminosi. La stessa cosa che fa un prisma a dispersione.

Ha senso, però, anche un’azione leggermente diversa: invece di spostare il rivelatore o allungarlo in qualche modo, possiamo lavorare sullo specchio, eseguendo moltissime scanalature vicinissime una alle altre. Capita che uno specchio del genere può dar luogo a riflessioni multicolori a seconda di dove viene colpito. E’ difficile da costruire? Nemmeno per sogno… pensate a un disco microsolco o a un “compact disc” come quello di Fig. 24.

Se vi dicessi che da questa semplice descrizione si arriva, con qualche difficoltà leggermente superiore, ai raggi laser e agli ologrammi e molto altro, vi stupireste ancora? No, penso proprio di no. Peccato non poter entrare nei dettagli, ma se analizzassimo tutti i fenomeni legati alla luce, non finiremmo mai. Resta il fatto, però, che la QED non ha alcun problema a descriverli tutti.

I reticoli naturali

Anche la Natura, però, ci sa fare e sfrutta lo stesso principio. Pur rischiando di andare un po’ oltre, vale la pena parlare del sale. Sì, proprio il sale da cucina. Sappiamo tutti benissimo che è composto da un mix di atomi di Sodio e di Cloro, legati saldamente tra loro secondo una struttura ben definita. Insomma, è uno dei tanti composti che hanno una struttura “cristallina”. Le distanze tra gli atomi sono quindi ben codificate.

Capita così che gli atomi si comportino come zone riflettenti di uno specchio e formino un reticolo di diffrazione quasi perfetto. In particolare, esso è particolarmente utile per i raggi X, luce che normalmente non si vede e che ha un cronometro che viaggia ben 10 000 volte più veloce di quelli della luce visibile. Possiamo, però, costruire un rivelatore per questi raggi e, attraverso la risposta che viene data spostandolo in posizioni diverse, stabilire la distanza tra gli atomi, ossia il “passo” del reticolo.

Ciò è già stato possibile nel lontano 1914, quando si è studiata per la prima volta la struttura dei cristalli, senza dimenticare che è stata una prova fondamentale per dimostrare che i raggi X fanno parte della radiazione elettromagnetica, ossia della luce. Ciò che avviene è descritto sommariamente in Fig. 25. Dobbiamo ammettere che alla natura piace proprio la QED, anche se la rende un po' più pazza e un po' meno comprensibile.

L’unione fa la forza… ma anche la debolezza

Concludiamo  con una constatazione di grande importanza per tutta la QED e la MQ. Avere dimostrato che qualsiasi parte di uno specchio contribuisce al fenomeno della riflessione ci dice che ogni parte dello specchio ha una sua freccia per qualsiasi evento possa avvenire, ossia qualsiasi possibilità ha una sua (ampiezza di) probabilità di verificarsi. In breve: tutto ciò che può capitare, prima o poi capita…

In altre parole, ancora, la singola freccia di ogni parte dello specchio ha una sua ampiezza di probabilità e quindi una probabilità di avvenire. Queste probabilità sono tutte uguali, perfettamente uguali. Non è quindi la probabilità di un singolo elemento a condizionare il risultato finale, ma la loro combinazione.

Abbandoniamo gli specchi e immergiamoci nella rifrazione. “Immergersi” è proprio il verbo adatto, in quanto studieremo come la luce passa dall’aria all’acqua.

Non aspettatevi niente di straordinario. Ormai la cosa veramente straordinaria l’abbiamo fatta nostra, utilizzando le frecce di probabilità -e la loro combinazione- per calcolare come e dove si ha la massima probabilità di ottenere un certo risultato. Passare dalla riflessione alla rifrazione non ha, quindi, bisogno di leggi diverse e di parametri particolari (come invece avremmo bisogno con l’ottica geometrica). Il succo di tutto è disegnare la direzione della freccia di ogni tragitto del fotone. Ma questo dipende solo e soltanto dalla lunghezza del percorso (o dal tempo impiegato a percorrerlo,  misurato con il cronometro).

L’ampiezza di probabilità (freccia) relativa a ogni tragitto è, infatti, sempre la stessa, ma cambia di più o di meno la direzione della lancetta del cronometro, ossia la direzione delle singole frecce. Il tragitto che viene scelto (ossia che ha maggiore probabilità di verificarsi) è quello intorno al quale la lancetta resta praticamente nella stessa direzione, ossia quello di minima distanza tra sorgente e rilevatore e, ovviamente, anche di minimo tempo di percorrenza. Ma non sempre minimo tempo e minima distanza coincidono.

Queste frasi, ormai banali, ci dicono qualcosa di veramente importante che non deve scapparci e che è l’essenza stessa della MQ. Qualsiasi direzione prenda un fotone uscendo da una sorgente, la “particella”(continuiamo a chiamarla così) ha la stessa probabilità intrinseca di colpire un bersaglio. Insomma, può andare dove vuole e può arrivare comunque a segno. Tuttavia, la direzione dell’ampiezza di probabilità (freccia) varia in funzione del tempo che il fotone impiega per raggiungere la meta. Solo la combinazione delle frecce decide qual è la direzione favorita. In alcuni casi le frecce si arrotolano tra di loro e annullano la loro intrinseca probabilità o, al limite, la diminuiscono. In altri casi le frecce si distendono lungo una direzione quasi costante e la probabilità finale cresce decisamente. Solo studiando questo comportamento si può calcolare quale sia il tragitto più probabile, senza aver bisogno di sapere niente a priori. Nel caso della riflessione è anche il tragitto di minima distanza.

E’ o non è una conquista fantastica? Tutti i fenomeni luminosi vengono trattati con lo stessa identica e banale regola. Basta solo fare attenzione e applicarla correttamente. Ne consegue che dobbiamo continuare a usare sempre e comunque lo stesso tipo di procedimento utilizzato finora: niente di meno e niente di più.

Fatemi fare un esempio di tipo “politico”: due gruppi di persone vogliono unirsi per cercare di governare saggiamente la loro Nazione.

Il primo gruppo ha molta passione e volontà, ma ciascun individuo ha le proprie idee su come ottenere un certo risultato. Possiamo anche dire che ognuna ha una sua validità, ma troppo particolare. Bisognerebbe formulare una linea di condotta unitaria, fatta di piccoli compromessi, ma con una direzione ben precisa nella mente di tutti. Niente da fare. Il loro tempo viene sprecato a discutere e a cercare di distruggere le idee dei compagni piuttosto che unire gli sforzi. Il gruppo lavora moltissimo ma, alla fine, non ottiene niente e si sfalda: il loro partito non nascerà mai.

Il secondo gruppo ha idee altrettanto valide e anche personali, ma mette la singola convinzione in libero confronto con quelle degli altri.  Cerca di estrarre le linee guida più unitarie possibili. Si accettano dei piccoli compromessi, non vince una sola idea, ma una combinazione di molte idee, abbastanza vicine tra loro. Dopo un tempo relativamente breve si forma il partito che riesce facilmente  a convincere la popolazione a votarlo.

Fermi tutti! Non ridete… non è certo un esempio che calza con la politica odierna… è solo un sogno di fantapolitica al servizio di una Nazione, ma penso renda bene l’idea di base. In fondo, in fondo, per avere risultati corretti e condivisibili da tutti, basterebbe che anche le menti e i desideri dell’uomo seguissero le leggi della MQ . Le leggi della MQ sono improntate alla più larga libertà di azione, sapendo, però, che solo l’unità di intenti porta alla soddisfazione vera e completa. Se ogni mente umana seguisse le regole della QED (del buon senso e della ragione?), come fa un cristallo di sale, vivremmo in un mondo libero, felice, aperto e democratico!

Un uomo in mare!

Torniamo alla QED e dimostriamo subito come lo stesso procedimento usato per la riflessione funzioni perfettamente anche per la rifrazione della luce. L’esperimento consiste in un fotone che parte da una sorgente situata nell’aria e deve arrivare a un rivelatore posto in fondo a un lago, a un fiume o a un mare. In parole povere, la luce passa dall’aria all’acqua. Vi prego di non dirmi: “il rivelatore smetterebbe subito di funzionare!” Lasciatemi costruire un rivelatore indistruttibile!

Disegniamo velocemente la Fig. 26. In alto vi è il nostro “lago” o “mare”, con la sorgente S e il rivelatore “subacqueo” R. Come al solito, i tragitti che prende il fotone possono essere qualsiasi. Poi, arrivati sulla superficie dell’acqua, si dirigono tutti verso R. L'evento da studiare è : raggiungere R partendo da S. Bisogna calcolare dove si ha la massima probabilità di riuscita.

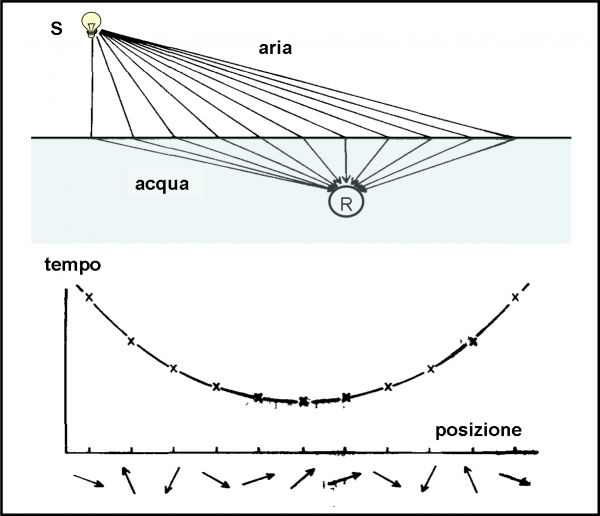
Attenzione, qualcuno potrebbe dirmi: “Perché dobbiamo considerare il cammino del fotone sempre rettilineo? E’ vero che sta andando dove vuole, ma potrebbe anche andarci seguendo linee curve…”. Avrebbe completamente ragione. E non potremmo nemmeno dire che il raggio è perpendicolare a un’onda circolare (è severamente vietato!). Tuttavia, nessuna paura: la QED ci mostrerà tra non molto che è proprio lei che descrive il moto rettilineo. Ne sa veramente una più del diavolo…

Torniamo alla Fig. 26. Sotto alla nuova configurazione, utilizzando sempre solo la luce rossa e il prezioso cronometro, riusciamo facilmente a tracciare la ben nota curva posizione del punto d’incontro con l’acqua in funzione del tempo di percorrenza e, conseguentemente, le ampiezze di probabilità (le frecce) per ogni punto considerato, con la loro direzione. Sembra di ripetere pari pari quanto fatto per la riflessione. Il risultato sembra anche lo stesso. Basta infatti combinare le frecce e otteniamo, in Fig. 27, la freccia finale che indica la probabilità di raggiungere il ricevitore. Ancora una volta, questa è piuttosto alta e il suo massimo contributo l’ottiene dalle frecce vicino al minimo della curva posizione-tempo, dove tra un punto e l’altro la lancetta del cronometro cambia di poco.

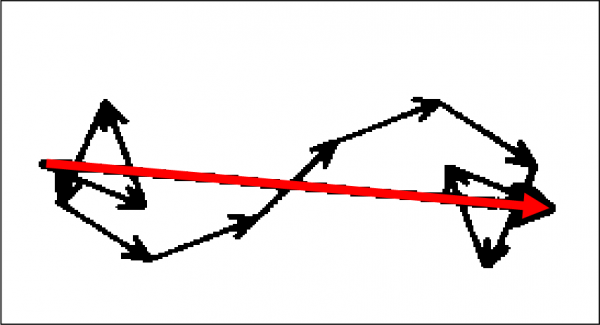
Attenzione, attenzione. Non concludiamo troppo frettolosamente! Finora abbiamo sempre detto che il tragitto percorso nel tempo minore è anche il tragitto di minima distanza. Vale ancora questa relazione? Siamo costretti a dire di NO. Questa uguaglianza vale solo nel caso che la velocità del cronometro sia sempre la stessa. Nella riflessione ciò è vero: l’intero percorso viene effettuato nell’aria, ossia in uno stesso tipo di “materiale” (lo specchio viene solo toccato…). Adesso, invece, il percorso viene effettuato parte nell’aria e parte nell’acqua. Dobbiamo accettare che cambi la velocità del cronometro nel completare il suo ciclo probabilistico. In altre parole, sembra proprio che la velocità della luce sia diversa. Non preoccupatevi. Non ci lasciamo convincere solo dalle parole. Tra non molto, descriveremo anche questo fatto! Per adesso accettiamo che il percorso minore non coincide con il tempo minore. A noi, però, interessa quest’ultimo, perché è proprio lui che comanda la direzione costante della lancetta. Ciò non capita dove il percorso é minimo, ma dove è minimo il tempo di percorrenza (è il cronometro che fa girare la lancetta). Scusate le ripetizioni, ma il concetto è troppo importante per non farlo nostro.

Per comprenderlo ancora meglio, facciamo un esempio veramente “estivo” in Fig. 28: tutti al mare, tutti al mare...  Siamo in una spiaggia famosa e intasata (proprio ciò che io detesto, pazienza…), in cui vigila dalla sua torretta un bagnino B. In mezzo a tanta ressa, ecco che qualcuno o qualcuna (N) si spinge troppo al largo o, magari, ha avuto un crampo. La situazione può diventare tragica e il bagnino si lancia velocemente in acqua per effettuare il salvataggio. Anch’egli, come un fotone, ha davanti a sé molte possibilità.

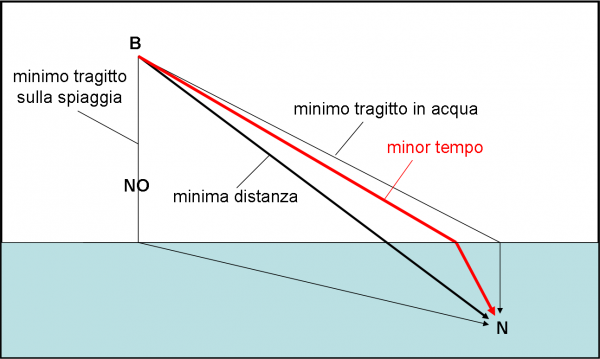
Di certo non sceglie una direzione opposta al mare! Tuttavia, la decisione non è del tutto banale. Anche se lui è un ottimo nuotatore sa benissimo che corre più velocemente di quanto non nuoti. Anch’egli è costretto a rallentare una volta entrato in acqua. Quale percorso dovrebbe scegliere per raggiungere N? Sicuramente non va dritto verso il mare, dato che poi avrebbe un tratto di nuoto eccessivamente lungo. Le scelte si restringono a due possibilità più ragionevoli: o sceglie il percorso di distanza minima, il più corto “in linea d’aria”, ma con un tratto di nuotata abbastanza lungo oppure sceglie di ridurre al minimo il percorso da effettuare in acqua, anche se comporta un tragitto più lungo da fare a piedi (ma correndo va più veloce).

Possiamo già notare che molto dipende dalle capacità del bagnino: se è un gran corridore sceglie la seconda opzione, se , invece, è un fantastico nuotatore può scegliere la via più corta. O, magari, anche dalle condizioni del mare (quanto rallenta il cronometro). In ogni modo, la decisione rimane sempre compresa tra queste due possibilità. L’importante è che impieghi il minor tempo per soccorrere N. Ovviamente non possiamo pretendere che il bagnino si fermi a fare i calcoli e quindi lui sceglierà più rozzamente. Noi, invece, conoscendo le sue potenzialità e avendo misurato i tratti di spiaggia e di acqua, sappiamo calcolare esattamente (con la solita regola probabilistica della QED) il percorso che viene effettuato nel minor tempo possibile (QUI il calcolo del percorso più veloce effettuato con metodi "classici").

Esso sarà quello rosso, una specie di compromesso tra quello con meno acqua e quello di minore distanza. Notate che il tragitto più probabile, deciso dalla QED, ci mostra un fatto non certo sconosciuto: il fotone-bagnino cambia la propria direzione una volta entrato in acqua. Vi dice niente il fenomeno della rifrazione luminosa? La Natura, cari amici, segue le regole della QED e fa piegare il raggio in modo da salvare lo sfortunato bagnante. E tutto ciò, utilizzando solo e soltanto le regole probabilistiche della MQ.

Un piccolo esercizio

Si potrebbe considerare un altro fenomeno molto interessante, di cui avevo già abbondantemente parlato nelle “lezioni” di ottica (QUI). Parlo del “miraggio”. Esso si manifesta, ad esempio, quando si guida lungo una strada in una caldissima giornata di luglio e la strada appare come se fosse bagnata. In realtà, ciò che si vede è il … cielo. Noi pensiamo immediatamente che la strada sia bagnata, dato che “normalmente” si vede il cielo in terra solo quando vi è uno strato d’acqua che lo riflette parzialmente (leghiamo, più o meno inconsciamente, un effetto alla causa più “comune” che può averlo prodotto).

Tuttavia, il cielo si riesce a vedere per terra anche quando la strada NON è bagnata e il fenomeno prende il nome di miraggio. Per risolvere il problema con la MQ, bisogna solo sapere che la luce viaggia più lentamente (il famoso cronometro) dove l’aria è più fredda e che il guidatore si trova in  uno strato d’aria più fredda rispetto a quella vicinissima all’asfalto. Il discorso è esattamente lo stesso del bagnino… e lo lascio a voi. Divertitevi e mettete alla prova le capacità raggiunte nell’applicare la QED a fenomeni spiegabili con l’ottica geometrica.  Per aiutarvi inserisco la Fig. 29 che rappresenta la situazione, con il guidatore posto in G.

Andare dritti conviene

Come vi avevo promesso, affrontiamo, ora, il problema del tragitto rettilineo della luce. Sembrerebbe un “atto di fede” e, invece, la QED non ha problemi a spiegare che è un risultato spiegabilissimo (con le sue regole). In altre parole, dimostriamo perché possiamo tranquillamente utilizzare percorsi rettilinei dei fotoni in qualsiasi mezzo stiano viaggiando.

Cosa ci dice la visione altamente democratica della QED? Un fotone è libero di andare dove vuole e come vuole. La probabilità di ciascuna di queste “scelte” è sempre la stessa. Esso può benissimo muoversi attraverso linee curve e strane quanto volete. Disegniamo la Fig. 30. Consideriamo dapprima le linee continue che uniscono la sorgente S e il rivelatore R. Non abbiamo niente tra di loro, solo un mezzo come l'aria. Come dicevo, tutte e tre le linee hanno la stessa probabilità di essere percorse. Tuttavia, noi siamo interessati a sapere qual è quella che viene veramente scelta. I fotoni sono liberi, ma non … stupidi!

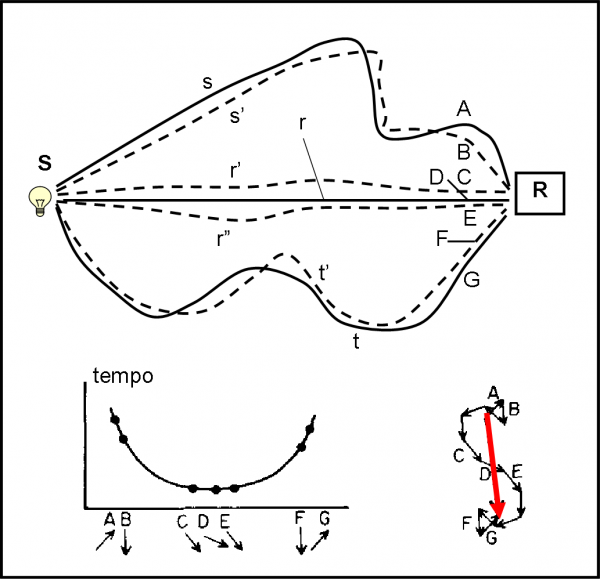
Immaginiamo, quindi, che i tragitti abbiano uno scambio di pensieri e di idee con quelli a loro più vicini. Anzi, è meglio dire che ogni traiettoria possibile tenga sotto controllo quelle vicine. Queste ultime siano rappresentate dalle linee tratteggiate. A questo punto è “ovvio” introdurre la solita regola della combinazione di ampiezze di probabilità. Se è vero che le strane traiettorie s e t hanno vicino  delle altrettanto strane traiettorie s’ e t’ che differiscono di poco da loro, è anche vero che le traiettorie r’ e r’’ differiscono molto meno dalla traiettoria rettilinea r.

Il tempo impiegato a percorrere le varie traiettorie segue perfettamente quanto fatto finora per la riflessione e rifrazione. Se disegniamo il grafico tempo-posizione del percorso otteniamo la solita “parabola” che ben conosciamo. Come posizione, possiamo tranquillamente prendere quella misurata lungo una qualsiasi retta verticale che taglia le linee. Come le altre volte, ciò che conta è, però, che per traiettorie molto elaborate e decisamente più lunghe, una leggerissima variazione comporta, alla fine, una differenza di tempo impiegato significativamente diverso da quello della traiettoria vicina di casa.

Cosa vuol dire questa constatazione? Dovrete ormai saperlo molto bene: la lancetta del cronometro forma un angolo decisamente grande con quella vicina (siamo nella parte alta della parabola). Se invece consideriamo linee che si avvicinano al minimo percorso (quello rettilineo) le differenze in direzione della lancetta si fanno piccolissime, dato che i tempi per effettuare questi tragitti sono praticamente uguali. Non ci resta allora che combinare le frecce relative a tutti i tragitti per  avere la solita conferma: le frecce lontane dal tragitto minimo si attorcigliano e la loro combinazione non porta a niente. Solo quelle vicino alla traiettoria rettilinea si sommano in modo costruttivo. La massima probabilità totale è merito loro, ossia sono proprio loro a descriverla e renderla alta. La probabilità massima si ha scegliendo una traiettoria rettilinea.

E’ importante notare ancora una volta (se ce ne fosse bisogno) che non è la probabilità della singola traiettoria (anche se è quella perfettamente rettilinea) a decidere il percorso di massima probabilità che ha la luce per andare da S a R, ma solo e soltanto l’insieme di molti percorsi talmente simili da far sì che le loro ampiezze si sommino effettivamente, raggiungendo tutte assieme un valore decisamente più alto di quelle frecce che perdono il loro tempo girando in tondo senza concludere niente.

Permettetemi un’analogia un po’ azzardata: è come se il fotone che va in linea retta “odorasse”  le traiettorie vicine (come se fossero percorse anch'esse da fotoni "virtuali") e si muovesse all’interno di una piccola fascia di amici, stando bene attento a non allontanarsi troppo da loro. L’unione fa la forza! Possiamo, perciò, concludere che la luce NON va in linea retta per chissà quale strana legge fisica, ma solo perché è la traiettoria che le permette di combinare nel modo migliore e più redditizio le frecce vicine. E’ lo stesso identico risultato che avevamo trovato per la riflessione!

Vicini amichevoli, ma che non siano pochi

Un’ulteriore constatazione che ci verrà estremamente utile tra poco. Affinché l’unione di frecce con la stessa direzione faccia sentire il suo “peso” probabilistico, e necessario che la traiettoria abbia attorno a sé un numero sufficiente di amici, ossia di frecce da sommare. Se lo specchio, ad esempio, fosse troppo piccolo, la probabilità totale che riesce a formarsi potrebbe non differire molto dalla probabilità finale di un gruppo di traiettorie completamente strambe, ma molto vicine tra loro. Insomma, lo specchio non funzionerebbe molto bene e ben poca luce raggiungerebbe il rivelatore.

Tuttavia, dovremmo cambiare la conclusione che siamo abituati a trarre nella vita normale. Invece di dire: “Lo specchio è troppo piccolo e non riesce a riflettere” si deve dire: “Il fascio di traiettorie che colpisce lo specchio non riesce a costruire una probabilità finale di ampiezza sufficiente a superare quella di altri fasci vicini diretti in direzioni qualsiasi”. Pensateci bene e noterete una differenza sostanziale!

Quello che vale per uno specchio, però, vale anche per il suo esatto contrario (o quasi): un  foro in cui la luce può passare tranquillamente.

Questo facile esperimento, che può diventare veramente importante,  lo studieremo  tra non molto,quando toccheremo -senza nemmeno volerlo- il principio di indeterminazione di Heisenberg. Anzi, ci renderemo conto che lavorando con la QED diventa un’ovvia conclusione, di cui si può anche fare a meno… Si fa per dire, ovviamente…

Una considerazione abbastanza importante. Non è assolutamente vero che i fotoni che rimbalzano sul primo specchio devono sapere cosa fanno quelli del secondo specchio. Basta ragionare in termini di probabilità finale (ossia con le regole della QED) e tutto diventa logico (nella sua illogicità). In parole semplicissime: ciò che noi vediamo come fenomeno fisico non è altro che un gioco eseguito da traiettorie  che camminano vicinissime tra loro. Il fenomeno SEMBRA avvenire in un solo modo, ma è più vero dire che il fenomeno avviene dove la probabilità è massima, seguendo regole perfette e perfettamente descrivibili. Vi stupirete di come sarà semplice descrivere una lente… Cominciamo, però, a vedere come "certe" assurdità stanno scomparendo come neve al Sole.

Un'ulteriore riflessione prima di andare avanti. Non la inserisco per creare confusione, ma solo perché temo che a qualcuno la trattazione della QED potrebbe sembrare qualcosa che poco ha a che vedere con la MQ “classica” che abbiamo imparato a conoscere attraverso vari fenomeni ed esperimenti apparentemente assurdi. Parole come  “collasso d’onda” e cose analoghe sembrano del tutto trascurate. Ci limitiamo a ripetere, quasi con monotonia, la solita regola che cambia di pochissimo di volta in volta. Sì, tutto bellissimo, ma sembra quasi che i misteri affascinanti e assurdi della MQ non esistano più.

La QED è figlia prediletta della MQ

Per richiamare l’attenzione e ricordare che QED e MQ sono la stessa cosa, facciamo un piccolo ragionamento. Ciò che abbiamo imparato è che la direzione presa da un fotone dopo che è partito dalla sorgente può essere qualsiasi. Non solo, però. Esso ha una sua ampiezza di probabilità intrinseca che è la stessa, qualsiasi direzione prenda. Chiamiamolo pure “particella”, ma sappiamo benissimo che può trovarsi dovunque a un certo istante. A parità di tempo anche la lancetta del cronometro è uguale, qualsiasi sia la direzione presa, per definizione.

Abbiamo, però, imparato che la descrizione di un fenomeno, come la riflessione o la rifrazione, avviene quando un certo numero di traiettorie possibili, non troppo piccolo, mantiene una direzione quasi uguale, ossia riesce a combinare efficacemente le singole frecce (i tempi di arrivo in un certo luogo attraverso una cera traiettoria) e acquista un’ampiezza di probabilità più alta di qualsiasi altro gruppo che arrivi sul rivelatore. Questa modalità (traiettoria) diventa la più probabile, ossia quella che “normalmente “avviene. Tuttavia, non dimentichiamoci che le traiettorie percorribili dal fotone arrivano sul rivelatore sempre e comunque con una probabilità uguale a quella di ogni altra sorellina, qualsiasi sia la strada percorsa.

Non confondiamo, quindi, probabilità che si verifichi un certo evento con  probabilità del singolo fotone di partecipare a tale evento in modo costruttivo. Durante il suo viaggio, quindi, qualsiasi direzione del fotone è valida tanto come le altre. Se poi diventa utile per il fenomeno conclusivo è solo una questione di condivisione con altri fratelli di idee simili, sulla scelta del percorso. Tuttavia, il singolo fotone non dirà mai cosa vuole veramente fare fino a che non farà fermare la lancetta del cronometro in un certo luogo. In ogni istante precedente la sua probabilità di essere ovunque è la stessa, piccola, ma reale.

Immaginiamo di seguire come una spia il nostro fotone che sta viaggiando senza comunicare la sua direzione. Non sappiamo dove sia, ovviamente, ma ci affidiamo alla fortuna e al tempo a disposizione: se non va bene con un fotone riproveremo con altro. Finalmente, a un certo momento, gli scattiamo una foto o lo fermiamo con un mano o anche solo lo guardiamo. Cosa abbiamo fatto? Abbiamo stabilito dove si trova esattamente e ovviamente, essendo proprio lì, la sua probabilità di trovarsi in quel luogo diventa il 100%. Non importa come sia disposta la lancetta del cronometro, ciò che conta è che l’ampiezza di probabilità raggiunge il 100%. Immediatamente, tutte le ipotetiche (?) direzioni alternative del fotone cessano di avere validità e scompaiono. Quell’insieme di particelle “virtuali”, ognuna delle quali avrebbe potuto essere quella vera del fotone, spariscono e l’unica particella rimane quella che visto o sentito. L’ho fatta collassare! Vedete come siamo velocemente arrivati a bomba? Visione probabilistica in cui esiste un'ampiezza di probabilità uguale in ogni direzione si trasforma in un qualcosa di veramente concreto che ha l’intera probabilità possibile di esistere lì e solo lì.

Non voglio proseguire in questa direzione perché renderei più complicata una trattazione che deve tener conto di vari principi da un lato e di una semplice regola dall’altro. Affidiamoci a quest’ultima e vedremo che, alla fine, tutto combacerà perfettamente. E salveremo sia le onde (di probabilità) sia le particelle che, da quanto detto, sono la stessa identica cosa. Quando questa perfetta identità ci apparirà chiara e illogicamente logica, potremo dire di aver cominciato a saper descrivere la MQ e a calcolare qualsiasi risultato di qualsiasi fenomeno elettrodinamico e non solo. Scopriremo anche che tanti principi della MQ perdono di valore o -meglio- nascono automaticamente descrivendo la QED.

Se vi dico che Feynman è un  genio assoluto non lo dico tanto per dire! Lo vedremo tra poco quando descriverà con un facilità irrisoria una lente capace di focalizzare la luce di una sorgente in un punto. Sarà un procedimento talmente ovvio da farci pensare che siano le nostre spiegazioni classiche a essere assurde e non il mondo di Alice.

Bando alle ciance e andiamo avanti. Innanzitutto dedichiamoci a scoprire e quantificare meglio le  capacità di un gruppo omogeneo e ben affiatato. Vorremo stabilire dei limiti alla consistenza di un  gruppo affinché sia veramente efficace nel “costruire” e/o definire l’evento di massima probabilità.

Come deve essere un vero “gruppo” quantistico

Per far ciò, non abbiamo bisogno né di specchi né di acqua, ci basta l’aria.  Si abbia la solita sorgente S  e due ricevitori R1 e R2. Vedremo tra poco dove piazzarli. Dato che siamo interessati a studiare il “fascio” di traiettorie che può costruire una probabilità vincente, non ci resta che limitare il gruppo da analizzare. Usiamo uno schermo di cartone o quello che volete (basta che blocchi la luce) con una fenditura al centro, come mostrato in Fig. 31.

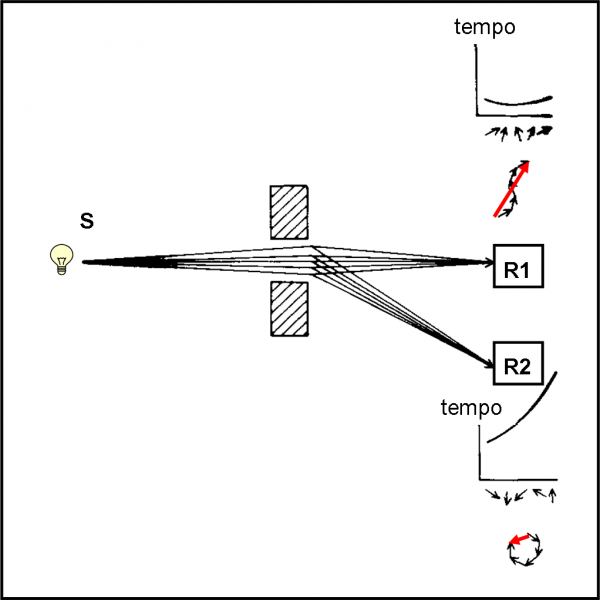
La fenditura non fa altro che limitare le traiettorie  che partendo da S cercano di raggiungere il rivelatore. Poniamo R1 di fronte alla fenditura e R2 in una posizione nettamente più bassa. Ormai sappiamo bene che prima di dire che la luce viaggia da S a R1 con la maggiore probabilità (cosa che l’apparenza del mondo comune sembrerebbe facilmente dimostrare), dobbiamo costruire il grafico che ci indica il percorso effettuato dalle traiettorie che riescono a passare e, con l’aiuto del cronometro, la direzione di ogni singola probabilità. Essendo il tragitto SR1 il più corto e dato che il mezzo da attraversare è sempre lo stesso, sappiamo benissimo che le frecce si sommeranno in modo costruttivo, differendo di pochissimo in quanto a tempi di percorrenza. Prendiamo pure una fenditura abbastanza larga, tanto per cominciare, e poi la stringeremo sempre di più, proprio per capire fino a che punto si può ridurre il gruppo delle traiettorie vincenti.

Per maggiore sicurezza (anche se già ci immaginiamo il risultato) leggiamo anche ciò che dice il rivelatore R2. Il discorso è sempre lo stesso: le frecce intorno alla traiettoria rettilinea SR1 si sommano nella parte centrale e danno una grande probabilità al gruppo corrispondente. Quelle, che invece colpiscono R2 (facendo un percorso un po’ strano ma SEMPRE possibile) litigano fra loro, si annodano e danno un risultato praticamente nullo. In poche parole ben poca luce raggiunge R2, come ci saremmo aspettati vivendo la realtà comune.

Tuttavia. Vediamo che anche buona parte delle traiettorie che arrivano in R1 servono a poco. Beh … lo sapevamo già: quelle più al bordo impiegano troppo tempo rispetto a quelle centrali e le loro frecce non costruiscono niente di buono. A questo punto, niente ci vieta di ridurre un po’ di più la larghezza della fenditura, in modo da fare entrare SOLO le traiettorie utili a costruire la probabilità finale. Il  risultato ci conforta: la probabilità della traiettoria QUASI rettilinea non cambia, e quella rivelata da R2 rimane ben poco significativa.

L’appetito vien mangiando (Fig. 32)… e riduciamo ancora di più la fenditura, che diventa molto piccola e taglia fuori anche molte delle traiettorie che sarebbero potenzialmente utili. Se la fenditura è troppo stretta, le cose si complicano di molto e ci riportano con i piedi per terra e rispolverano l’assurdità apparente della MQ. La luce che raggiunge R1 s’indebolisce. Niente di strano, dato che arrivano meno traiettorie. Tuttavia, anche la probabilità finale si riduce. Anche questo è ovvio, dato che abbiamo meno frecce da combinare assieme.

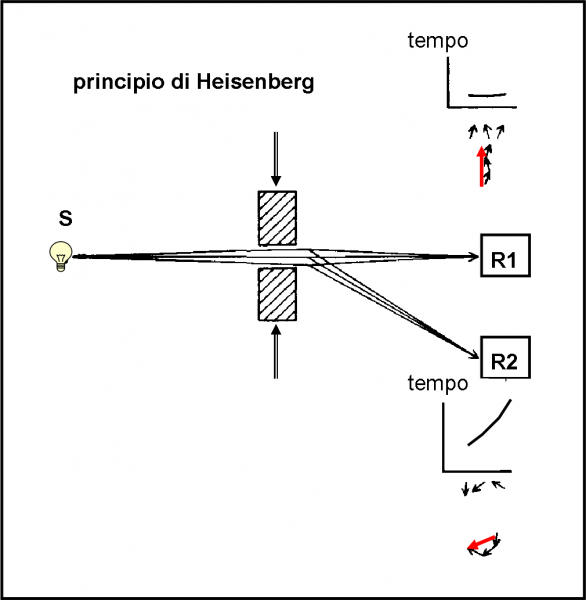
La sorpresa è, invece, che, improvvisamente, anche R2 comincia a rivelare fotoni e la loro probabilità finale diventa comparabile con quella ottenuta in R1. In poche parole, per una fenditura molto stretta la probabilità si sparpaglia su rivelatori posti anche molto distanti tra loro. La spiegazione è ovvia, in termini di QED. Benché i tragitti da S a R2, siano più lunghi di quelli da S a R1, le differenze tra di loro sono sempre meno evidenti e, a causa anche del piccolo numero di frecce da sommare, capita facilmente che la freccia finale abbia la stessa lunghezza.

La combinazione delle frecce relative a R1 e R2 le vediamo nella parte destra della Fig. 32. Ripetiamo ancora. Restringendo la fenditura, diminuisce l’intensità luminosa (ossia il numero di fotoni che arrivano o la probabilità  delle traiettorie ammissibili). Analogamente diminuisce, però, la probabilità finale del percorso considerato ufficiale (rettilineo e  più corto). Diminuisce a tal punto che anche  altri rivelatori, posti un po’ ovunque, possono ora competere con la probabilità, fino a quel punto dominante. Anzi, la loro probabilità aumenta grazie proprio al piccolo numero di frecce da sommare. In pratica, succede che, per una fenditura molto stretta la luce arriva in punti diversi dello schermo finale (ossia in rivelatori diversi) mantenendo una probabilità di accadere praticamente uguale. Non voglio assolutamente sconfinare nella diffrazione e cose del genere (ma è ovvio che la figura di diffrazione dipende dall’ampiezza della fenditura come ci insegna la QED). Diventerebbe un po’ troppo difficile, anche se è tranquillamente alla portata della QED e delle sue leggi. Sappiamo o non sappiamo che riesce a spiegare ogni fenomeno ottico?

C’è bisogno di Heisenberg?

Tuttavia, è giusto e doveroso fare una considerazione della massima importanza. Quando stringiamo la fenditura sempre di più, cosa stiamo facendo? Cerchiamo di determinare sempre meglio qual è la posizione del fotone prima che si diriga verso il rivelatore “prescelto”. Facendo questo, però, ci siamo accorti che diventa sempre più difficile prevedere probabilisticamente quale sarà la direzione scelta. Con la fenditura larga capita, invece, il contrario: non sappiamo molto bene dove passa il fotone all’interno del foro, ma sappiamo molto bene la direzione che prenderà dopo, con grande probabilità, ossia quella del rivelatore R1.

Ma che cosa  abbiamo appena enunciato? Sì, cari amici, nient’altro che il principio di indeterminazione di Heisenberg, uno dei capisaldi della MQ, proprio quello che ci permette di rendere plausibile la nascita dell’Universo e dell’inflazione. Vedete come tutto è strettamente collegato.

Senza i fotoni che scelgono una direzione e sommano le  freccette delle loro probabilità, il principio di Heisenberg rimarrebbe senza descrizione e di conseguenza il nostro Universo potrebbe non nascere o essere nato (che è, infondo, la stessa cosa). Ripeto ancora: il dire che se riesco a determinare con esattezza la posizione non riesco a determinare altrettanto bene la sua direzione (e viceversa) è un’ovvia conseguenza della QED. Il principio di Heisenberg potrebbe non essere nemmeno enunciato, dato che è un passaggio obbligatorio

Bene, ridendo e scherzando abbiamo imparato cosa s’intende per fascio stretto  e, soprattutto, che non bisogna esagerare a renderlo stretto e preciso, dato che subentra il principio di Heisenberg e tutto si complica. Complicazioni che sono perfettamente previste dalla QED.

La lente? Un piccolo e banale trucco probabilistico!

Affrontiamo, adesso, un’applicazione fantastica di tutto ciò che abbiamo imparato finora. Per la prima volta non saremo calcolatori passivi, ma cercheremo di “agire” in modo da ottenere un risultato altamente utile per le osservazioni “normali”. Useremo ciò che conosciamo delle regole della QED per costruire uno strumento fondamentale atto a osservare gli oggetti dell’Universo. Vi rendete conto dell’enorme portata concettuale di questa asserzione? Se solo Galileo Galilei avesse conosciuto la QED, non si sarebbe sorpreso più di tanto delle sue scoperte astronomiche…

Consideriamo la solita sorgente S e un rivelatore che questa volta chiamiamo F. Tra poco vedremo il motivo di questa scelta… I fotoni sono liberi di andare dove vogliono, come al solito, e di raggiungere F con qualsiasi traiettoria. Noi continuiamo a disegnare traiettorie rettilinee per pura semplicità, ben sapendo che lo possiamo fare senza alcun rischio.

Immaginiamo di tracciare una retta verticale “virtuale”  nella Fig. 33, che ci permetta di considerare solo le traiettorie che, arrivate su quella linea, piegano per andare verso F. Una scelta che però non lede minimamente le probabilità intrinseche di ogni singola traiettoria (la freccia è uguale per tutte, disegnate o no). Come rappresentiamo il solito diagramma tempo- posizione? Nel solito, addirittura noioso, metodo. Il tempo decresce andando verso traiettorie rettilinee e le frecce si muovono sempre meno rispetto alla precedente e alla successiva, avvicinandosi alla traiettoria che viene percorsa nel minor tempo possibile.

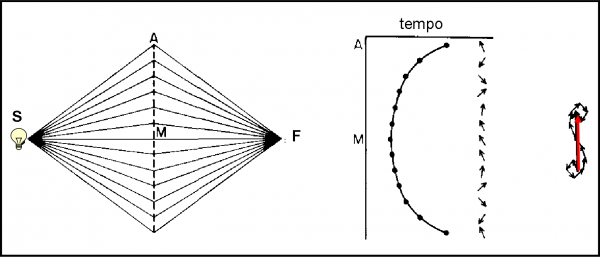
Prendiamo le frecce e componiamole assieme. Ancora una volta il centro della figura è favorito e le traiettorie vicino a quella di minimo percorso e di minor tempo (la rettilinea) hanno la massima probabilità di essere seguite.  Insomma, non abbiamo ottenuto altro che le frecce lontane si annullano e quelle vicine si sommano: una scarsa soddisfazione, senza aver imparato niente di nuovo.

Tuttavia, sappiamo anche che se un fotone attraversa un mezzo diverso, come l’acqua o il vetro, il cronometro gira più lentamente.  Perché allora non intervenire direttamente sulle traiettorie della Fig. 34 e costringerle a impiegare TUTTE lo stesso tempo per arrivare in F? Difficile? Mica tanto, basta inserire per ogni tragitto una parte di vetro da affrontare più lentamente (come il bagnino nell’acqua). Questa percorso in un mezzo diverso deve essere, ovviamente, più lungo per la traiettoria originariamente più veloce e praticamente nullo per quelle ai bordi della retta (A) che già impiegavano un tempo considerevole.

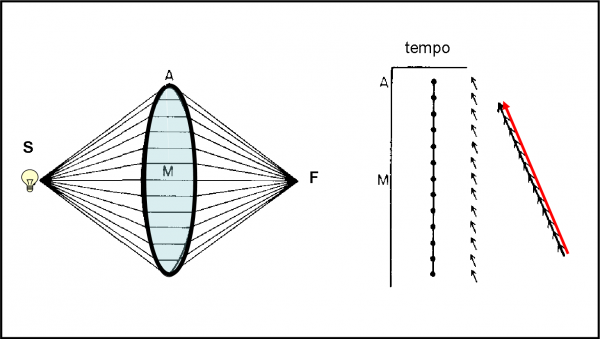
Insomma, inserendo un pezzo di vetro (l’acqua non è facile da maneggiare) possiamo costringere tutte le traiettorie  a essere percorse  nello stesso tempo per raggiungere il punto F. In tale caso come si trasforma la combinazione delle frecce di probabilità?

Facilissimo a dirsi e a calcolarsi: tutte le frecce sono lunghe uguali (per definizione) ma sono anche dirette tutte nella stessa direzione, dato che il tempo finale impiegato per passare da S a F è uguale per tutte (il cronometro, alla fine, ha la lancetta che punta sempre nella stessa direzione). Accidenti! Otteniamo una probabilità altissima, a cui concorrono TUTTE le traiettorie che colpiscono la retta “virtuale”. Questa ormai non ha più senso di essere disegnata: da come abbiamo agito, è stata sostituita da un pezzo di vetro di  spessore variabile, massimo nella direzione orizzontale SF e nullo nelle direzioni dei bordi.

Insomma, abbiamo costruito nientedimeno che una lente convergente, capace di produrre in F una probabilità altissima di ricevere tutta la luce che proviene da S e che incontra la lente. E l’abbiamo costruita fidandoci completamente (e giustamente) delle regole incomprensibili (lo sono ancora tanto?), ma descrivibili della QED.

Viene spontanea una conclusione logicissima in termini di MQ: se aumento la lunghezza della lente (il diametro)  la probabilità che tutta la luce raggiunga il fuoco sale notevolmente. Un modo diverso, apparentemente assurdo, per dirci che è meglio, quando si può, usare una lente il più grande possibile. Qualcosa in più del dire solamente: “Più è grande e più raccoglie luce”.

Geniale, decisamente geniale! La QED, senza alcuno strano artificio ci ha permesso di costruire uno strumento capace di concentrare, in un singolo punto, la luce di una sorgente con una probabilità altissima. Tutte le ricadute sul diametro, su lenti multiple, su fenomeni di aberrazione, su lenti divergenti, su ingrandimenti, ecc., ecc. vengono risolte e descritte continuando a ragionare con le stesse identiche regole. Tutta l’ottica dei telescopi può essere descritta in termini probabilistici, con l’uso di una freccia sempre uguale, un  cronometro preciso e una banale somma di vettori. E poi diciamo che la MQ è assurda! Comincia a sembrare più logica di tutte quelle sigle inutili che accompagnano i telescopi e la loro ottica. Oculari, lenti di Barlow, tipo di combinazione ottica, luminosità , campo di vista, ecc., ecc.? Nessun problema! Basta chiedere alla QED di seguire le sue solite regole che ormai conosciamo quasi perfettamente.

Chi vuole provare può farlo. Le difficoltà non sono poi insormontabili. Un esercizio, comunque, più utile che ipotizzare universi senza capo né coda…

Complichiamo un po' il processo di calcolo

Siamo arrivati a un  punto importante, direi a una svolta. Dopo aver imparato così bene a calcolare la probabilità che un certo evento avvenga, ecco che adesso vi chiederò di dimenticare per un po' la combinazione delle frecce di probabilità e di fare conoscenza con un nuovo tipo di calcolo, relativo a eventi che possono essere scomposti in singoli eventi, anche del tutto indipendenti tra loro.   Le difficoltà aumentano un poco, ma la preparazione che abbiamo dovrebbe essere ormai sufficiente a superarle. Nessuna formula o concetto astruso, ma una serie di trasformazioni che vanno seguite e comprese con particolare attenzione. Questo cambio di rotta impone anche un cambiamento di punto di vista. Finora abbiamo calcolato una probabilità finale considerando e "sommando" le probabilità di ogni strada che può portare all'accadimento di un certo evento. Adesso, invece, dobbiamo, per semplicità, considerare assodata la strada più probabile, che si porta, comunque, dietro il valore della sua probabilità, e calcolare come le probabilità di ogni pezzo di strada (considerato  stabilito) si combinano per determinare la probabilità finale.

Sembra un discorso particolarmente difficile e cercheremo di spiegare tutta la sequela di azioni da fare, con particolare attenzione, arricchendola di dettagli e di esempi. Cercheremo anche di spiegare, molto meglio, in cosa consiste questo cambio di "marcia". Non spaventatevi, però: è solo una questione di tecnica operativa e niente di più

Vedremo che, dopo questa ulteriore fatica, finalmente la parola “elettrodinamica”  acquisterà una sua logica. Ma dobbiamo attendere e avere pazienza…

Ricapitolando...

Abbiamo imparato a calcolare la probabilità di un evento che può verificarsi attraverso varie vie alternative. Come? Tracciando per ogni possibile percorso una freccia (secondo certe regole) e “sommandole” vettorialmente, in modo da ottenere una freccia finale. La freccia è stata chiamata ampiezza di probabilità e il suo quadrato è proprio la probabilità che l’evento si verifichi. Attenzione: abbiamo considerato tutte le vie possibili che un fotone può seguire, partendo da una sorgente S e raggiungendo un rivelatore R. Ripeto ancora: sono traiettorie alternative, indipendenti l’una dall’altra, che, però, finiscono nello stesso punto, o -meglio ancora- che soddisfano l'evento.

In questo modo, abbiamo considerato ogni possibile percorso della luce senza alcun favoritismo o preconcetto sul risultato finale (sia che lo conosciamo o no attraverso la realtà quotidiana). Solo la freccia finale ci dice con quale probabilità l’evento può avvenire e quali sono i percorsi che contribuiscono in modo preponderante alla sua riuscita. Possiamo, allora, concludere che questa è la strada che il fotone percorre con maggiore probabilità.

Abbiamo visto che il percorso che dà la massima probabilità di riuscita è quello di durata minima. Se l’evento avviene con la luce che attraversa solo un mezzo (aria, ad esempio), il percorso di minima durata è anche quello di minima distanza. Nel caso della riflessione semplice, ad esempio, questo percorso è quello di un fotone che rimbalza con un angolo di incidenza uguale all’angolo di riflessione, proprio come ci mostra la realtà di tutti i giorni. In realtà, sarebbe meglio dire che le traiettorie più probabili sono quelle che stanno abbastanza vicine a questa configurazione.

Le cose cambiano un po’ con la rifrazione e il percorso più probabile è sempre quello in cui si impiega il minor tempo, ma non coincide con quello di minima distanza (spaziale), dato che i fotoni devono passare da un mezzo (aria) a un altro (acqua o vetro).

Sfruttando questa caratteristica della luce, siamo anche riusciti a far arrivare su un unico punto, e con la stessa probabilità, tutte le traiettorie che in aria avrebbero impiegato tempi diversi. E’ bastato inserire un pezzo di vetro sagomato (lente) in modo che il tempo finale impiegato da un fotone fosse sempre lo stesso, indipendentemente dal punto del vetro colpito. Il fotone può toccarlo in qualsiasi punto, ma converge sempre sul fuoco contribuendo alla probabilità finale nello stesso identico modo che avrebbe fatto se avesse seguito il percorso più corto. Un risultato che conosciamo molto bene nel mondo comune e che viene usato per la costruzione dei cannocchiali e dei telescopi.

Ci siamo, però, anche accorti che se limitiamo troppo il fascio di traiettorie percorribili, può accadere che traiettorie più dispendiose in termini di tempo e distanza abbiano la stessa probabilità di essere seguite da un fotone, di quelle favorite intuitivamente (minima distanza e tempo). Un risultato contro intuitivo nella vita di tutti i giorni, ma che descrive, senza nemmeno averlo cercato, nientemeno che il principio di indeterminazione di Heisenberg. Non solo però… i più preparati possono vedere in questo risultato il punto di partenza per ottenere il celebre esperimento della doppia fenditura, proprio quello che dà la migliore rappresentazione dell’assurdità e della genialità dell’intera MQ. Potete anche provare a ottenerlo da soli, dato che tra non molto ci arriveremo con grande scioltezza.

A questo punto, possiamo eseguire (quando  diventa utile per non creare troppa confusione) una semplificazione che ormai ci possiamo permettere: consideriamo come traiettoria seguita dalla luce solo quella che dà il massimo contributo alla probabilità che l’evento si verifichi. Questa è, quasi sempre, proprio la traiettoria descritta normalmente dall’ottica geometrica. Non ditemi: “Ma allora perché abbiamo fatto tanta fatica e usato tanti artifici incomprensibili e solo calcolabili e non comprensibili?”. La ragione è una e una sola: trattare TUTTI i fenomeni legati alla luce e alla sua interazione con la materia è possibile solo attraverso una visione puramente probabilistica, perfettamente quantificabile, ossia attraverso la QED. Noi stiamo applicandola a fenomeni semplici e abbastanza intuitivi, ma la sua unicità diventa ben più visibile solo quando le difficoltà aumentano. Senza dimenticare, poi, la strana doppia natura della luce, che solo la MQ e la QED riescono a descrivere senza cadere nella pazzia. Forse, proprio perché sono teorie “pazze” e assurde per definizione…

Semplifichiamo

Torniamo a noi e descriviamo meglio cosa stiamo per iniziare a fare. Vogliamo studiare eventi che possono essere scomposti in due o più eventi. In altre parole, vogliamo calcolare la probabilità finale di un certo evento attraverso le probabilità dei singoli sotto-eventi che lo costituiscono. Tanto per fare un esempio, che tratteremo in dettaglio, pensiamo alla semplice riflessione di uno specchio. Nei capitoli iniziali abbiamo considerato tutte le possibili traiettorie con la loro singola probabilità e poi siamo riusciti a trovare quelle che davano il massimo contributo alla probabilità finale. Adesso, invece, consideriamo la traiettoria come stabilita e vediamo come la probabilità si trasforma ad ogni singolo passo dell’intero fenomeno.

Dobbiamo essere sinceri. Questo procedimento è un po’ più complicato di quelli adottati finora. Complicato, però, non vuol dire maggiore difficoltà concettuale, ma solo possibile confusione nella serie di operazioni da svolgere. Niente di tragico, ma è necessaria molta attenzione e pazienza. Capiremo subito il perché della semplificazione di cui abbiamo appena parlato e che è meglio ribadire ancora per non creare ulteriore confusione.

Quando facciamo partire la luce da una sorgente sappiamo benissimo che essa può andare in ogni direzione e molte traiettorie giungono sullo specchio, ciascuna con la propria freccia. In altre parole, abbiamo una dispersione della luce e non certo un solo raggio luminoso. Tuttavia, solo uno (o meglio solo un certo gruppo abbastanza stretto, ma non troppo) raggiunge il rivelatore dando origine alla massima probabilità.  Possiamo permetterci di disegnare solo quello, come, in fondo, abbiamo fatto all’inizio di tutto con l’esperimento della doppia riflessione? Sì, perché, ripetiamo ancora, ormai sappiamo benissimo come calcolare questa traiettoria. Praticamente è come assumere che ogni fotone che parte dalla sorgente arriva sul rivelatore attraverso un solo percorso, quello più probabile. Ciò è quello che ci direbbe l’ottica geometrica, ma noi sappiamo che è invece un’approssimazione che ormai ci possiamo permettere.

Un dovuto riassunto preparatorio

Luce, fotoni, raggi luminosi. Facciamo, ancora una volta, un po’ di chiarezza sul concetto che stiamo seguendo e che può confondersi con uno molto simile. Quando, normalmente, pensiamo a una sorgente luminosa, non ci è difficile immaginare che la luce vada in ogni direzione. Disegniamo questa configurazione spesso e volentieri attraverso i raggi luminosi. Tuttavia, in questo caso, ogni raggio può essere considerato un fotone singolo, ossia una vera e propria particella. Noi, invece, facciamo una cosa concettualmente molto diversa (e fondamentale per la MQ). Lo possiamo fare, solo perché lavoriamo in termini di probabilità e non di realtà fisica. Quando diciamo che la luce parte da S e che ogni direzione è possibile, intendiamo che un singolo fotone può andare in ogni direzione, dato che non abbiamo modo di sapere la sua traiettoria. Solo alla fine, attraverso il calcolo delle probabilità, e dopo aver stabilito esattamente l'evento che deve compiersi, possiamo dire quale è la più conveniente e probabile. Solo alla fine, ossia solo quando esso si comporta sicuramente come una singola particella, come ci dimostra il “tic” del rivelatore.

La conclusione può essere la stessa (prendere cento fotoni particelle e mandarle in molte direzioni o prendere un solo fotone di carattere ambiguo e tracciare le sue possibili direzioni), ma concettualmente la cosa è ben diversa e porta, alla fine, a una visione completamente diversa della Natura.

Nel primo caso diciamo che abbiamo tanti fotoni, ognuno su una direzione, e questa direzione può essere qualsiasi; nel secondo caso diciamo, invece, che il fotone, pur essendo una singola entità, può trovarsi ovunque! Nel primo caso facciamo fisica classica e leghiamo un’entità con un ben definito percorso, benché possa essere qualsiasi; nel secondo caso facciamo MQ in quanto ammettiamo che l’entità possa trovarsi ovunque, lungo qualsiasi direzione rispetto alla sorgente. Ecco perché mi sono permesso all’inizio di rappresentare questa “ubiquità” con l’idea delle particelle “virtuali”.

Capiamo, allora, anche perché, nel primo caso siamo obbligati, per spiegare certi fenomeni, come l’interferenza, a sostituire il termine particella con il termine onda e accettare una bimodalità inquietante. Una situazione veramente assurda, ma senza via d’uscita, dato che il rivelatore ci dimostra che il fotone è una particella, mentre l’interferenza ci dimostra che deve essere un’onda. Nel secondo caso, basta, invece, un'unica entità, capace di essere ovunque e di cambiare la propria natura al momento opportuno. In questa logica, la MQ è molto meno assurda della realtà!

Tanti passi per un solo risultato

Torniamo a noi con la  Fig. 35 e cominciamo, finalmente, con una descrizione del tutto generale del procedimento, proprio per meglio spiegare le operazioni da svolgere, che chiamiamo prodotto di frecce. Non entro nei dettagli, ma la parola ha un senso profondo perché si riallaccia proprio alla nascita di questa operazione fin dai tempi più antichi.

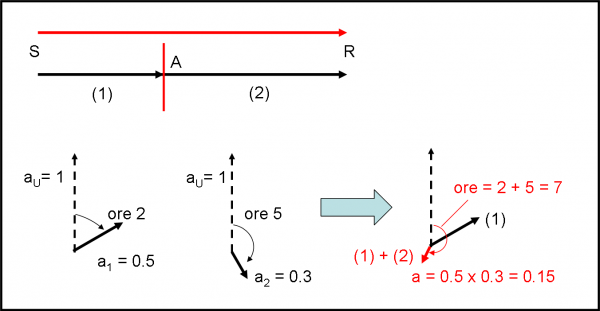
Consideriamo un evento che può essere scomposto in due eventi successivi (il numero, però, può essere qualsiasi). Ognuno di questi eventi ha una sua freccia di probabilità. Come poter passare dalla prima fino a quella conclusiva? Ecco il nostro problema. Disegniamo separatamente i due “passi” dell’evento, (1) e (2). Nel primo, la luce parte da una sorgente S e arriva fino a un certo punto A. Cosa succede durante il tragitto c’interessa poco, per il momento. Di sicuro la luce alla partenza ha una freccia di ampiezza UNITARIA con una direzione qualsiasi.

Scegliamo come direzione di partenza quella verticale, ossia con la lancetta del cronometro che indica mezzanotte. Questa è la posizione di angolo uguale a ZERO. Alla fine del primo tragitto ci dobbiamo aspettare che la freccia sia cambiata. Ha subito, infatti, due trasformazioni: un accorciamento e una rotazione. Questo fatto lo conosciamo benissimo. La freccia si accorcia perché la probabilità di arrivare fino ad A è minore di quella unitaria di  partenza (la luce può essersi riflessa, rifratta o qualsiasi cosa vogliate). La sua direzione è anche variata rispetto alla mezzanotte. Il cronometro, infatti, è partito subito e quando la luce arriva su A, la lancetta ha percorso un certo angolo.

In basso disegniamo la freccia che si ottiene. Ad esempio, essa si è ridotta del 50% (in termini di unità vale, quindi, 0.5) e la sua direzione è quella delle ore 2 (60°).  La luce continua con il secondo passo e va da A a R. Assumiamo, a questo punto, che A sia una nuova sorgente e calcoliamo come la freccia unitaria si trasformi nel secondo passo dell’evento. Ad esempio, la freccia unitaria si è accorciata fino a diventare 0.3. Inoltre, il tempo impiegato per passare da A a R è stato più lungo di quello del primo passo e la lancetta (ossia la direzione della freccia) si è portata da mezzanotte fino alle ore 5. Anche questo risultato è riportato nella parte bassa della figura.

Ciò che vogliamo calcolare adesso, conoscendo le singole trasformazioni della freccia, è la trasformazione finale, ottenuta combinando in qualche modo le due trasformazioni. Questo procedimento non è altro che il prodotto delle frecce, ossia delle ampiezze di probabilità.

La prima freccia ha lunghezza 0.5 alla fine del primo passo. Questa lunghezza si è poi ulteriormente accorciata. Di quanto? Proprio del prodotto tra 0.5 e 0.3, ossia la sua lunghezza finale vale 0.5 x 0.3 = 0.15. Perché posso fare semplicemente il prodotto delle lunghezze? Proprio perché esso mi indica di quanto la lunghezza della prima freccia si è ulteriormente accorciata dopo il secondo passo. Se, infatti, il secondo passo ha ridotto la freccia unitaria fino a 0.3, ha ovviamente ridotto una freccia di ampiezza 0.5 a un’ampiezza di 0.5 x 0.3, ossia 0.15. Guardate che sto dicendo cose veramente elementari. Praticamente sto spiegando il prodotto di due numeri. Il secondo accorciamento che fa passare  da 1 a 0.3, fa passare da 0.5 a 0.15, che è il prodotto dei due accorciamenti.

Ancora più semplice è il calcolo della posizione della lancetta finale. Basta sommare le ore: 2 + 5 = 7. Infatti, la seconda trasformazione ha ruotato la freccia unitaria di 5 ore. Questo vuol dire che se la freccia ottenuta alla fine del primo passo era diretta verso le ore 2, l’orologio ha ancora percorso 5 ore prima di fermarsi definitivamente alle ore 7. Perché tutto questo “pasticcio”? Perché non cercare di semplificare la trattazione parlando solo di ciò che succede, di volta in volta, alla freccia dopo ciascun evento parziale? La ragione è semplice: per poter trattare ogni sotto-evento come evento scollegato dagli altri. Solo dopo, a seconda di ciò che vogliamo ottenere, possiamo eseguire la trasformazione completa. Il risultato finale della freccia, andando da S fino a R, è rappresentato nella parte destra della figura, dove vi sono sempre, in bell’evidenza, la freccia unitaria e la direzione di partenza

Non preoccupatevi se la faccenda vi è sembrata un po’ difficile. Adesso l’applicheremo a casi già trattati e i dubbi rimasti scompariranno.

Possiamo, però, cercare di semplificare ancora. Ogni passo dell’evento complessivo porta a una freccia ridotta e ruotata. In pratica, basta considerare la freccia finale del primo passo, accorciarla di quanto dice in percentuale il secondo passo e continuare a far girare il cronometro. Idem con i passi successivi e alla fine si ottiene il risultato voluto. Insomma, accorciare, di volta in volta, una freccia, in base a quanto dice ogni singolo passaggio. Per la direzione della freccia, basta continuare a farla girare da dove era arrivata il passo prima. Insomma, scegliete il modo che preferite, ma tenete conto che l’importante è saper rendere indipendenti i singoli passaggi.

Riassumendo:

(a) Quando vogliamo calcolare la probabilità di un evento ottenibile con molte vie alternative bisogna sommare le frecce (ampiezze) di ogni via.

(b) Quando vogliamo calcolare la probabilità finale attraverso i vari passi di un evento, bisogna moltiplicare in successione le frecce (ampiezze) di ogni passo

Riflessione semplice

Prendiamo come esempio proprio l’evento forse più semplice trattato finora: la riflessione semplice. La “spezziamo”, nella Fig. 36,  in tre eventi singoli: 1) dalla sorgente allo specchio; 2) la riflessione; 3) dallo specchio fino al rilevatore R₁.

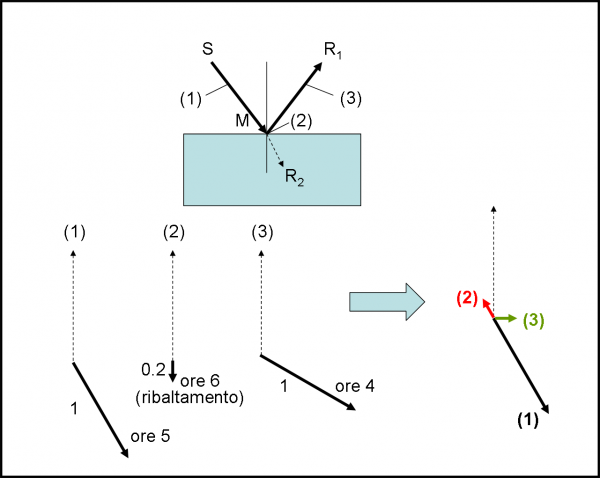
Voglio farvi notare che la riflessione in sé determina un  risultato che è legato al tipo di sostanza coinvolta (aria, vetro, acqua, ecc.). Per adesso accettiamo il risultato relativo senza chiederci “perché”. La motivazione la vedremo in seguito…

Il primo passo non comporta alcuna riduzione della lunghezza della freccia in quanto abbiamo assunto che tutti i fotoni che partono da S raggiungano R₁ o R₂ (una semplificazione che possiamo fare, dato che sappiamo bene come trattare le vie alternative) attraverso il percorso più probabile. La lancetta, però gira, dato che il tempo passa. Ad esempio, essa raggiunge le ore 5. Questo valore dipende solo e soltanto dalla distanza tra la sorgente e lo specchio.

Il secondo passo comporta (accettiamolo come un dato di fatto) una decisa riduzione di ampiezza che diventa 0.2. Accettiamo anche il risultato che la freccia faccia mezzo giro (si ribalti), ossia la lancetta segni le ore 6.

Il terzo passo è simile al primo: l’ampiezza non cambia, ma la lancetta potrebbe anche girare di più o di meno a seconda della distanza tra specchio e rivelatore R₁. Poniamo, ad esempio, che sia un po’ più corta e la lancetta del cronometro si fermi sulle 4.

Applichiamo la nuova regola di moltiplicazione e otteniamo che l’ampiezza finale è il prodotto delle tre ampiezze relative a ogni passo, ossia 1 x 0.2 x 1 = 0.2. La rotazione finale del cronometro è la somma delle rotazioni, quindi: 5 + 6 + 4 = 15 = 3. In pratica, è la somma dei due passi (1) e (3), a cui si aggiunge un capovolgimento del verso, dovuto alla riflessione aria-vetro.

L’ampiezza finale, quindi, vale 0.2 il che porta a una probabilità di 0.04, ossia il 4% della luce viene riflessa e raggiunge R₁. Il risultato è ovviamente uguale a quello che abbiamo descritto all’inizio delle lezioni.

Ricordiamoci sempre che tutte queste belle operazioni portano a risultati esatti delle probabilità finali, permettendoci di calcolarle con estrema precisione e, quindi, sapere come si comporta la Natura. Tuttavia, resta sempre incomprensibile il fatto che quattro fotoni su cento decidano di rimbalzare!

Nell’esempio precedente (riflessione semplice) possiamo anche seguire l’evento complementare, ossia quello che descrive la traiettoria che arriva fino al rivelatore R2, posto dentro al vetro. Anche questo è composto da tre passi: (1) tragitto sorgente-specchio; (2) passaggio attraverso la superficie del vetro; (3) tragitto, dentro al vetro, dalla superficie fino al rivelatore R₂. L’abbiamo rappresentato in Fig. 37.

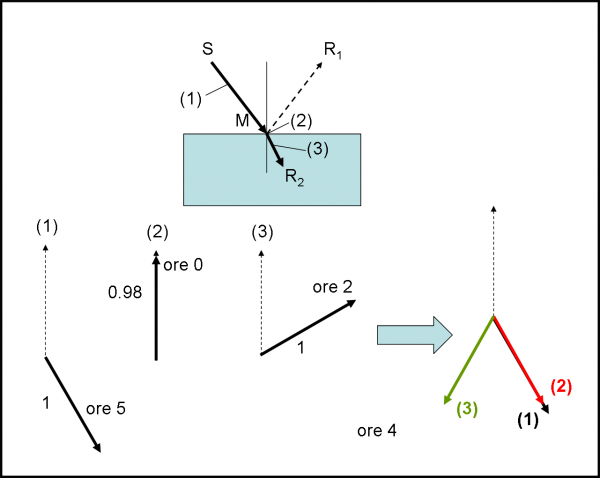
Il primo passo è identico a quello precedente, ossia ampiezza immutata e lancetta sulle ore 5. Il secondo passo causa una piccolissima riduzione della lunghezza della freccia unitaria portandola a 0.98. La lancetta, invece, non si muove. Il terzo passo è nuovamente analogo a quello della riflessione, ma avviene all’interno del vetro. La freccia unitaria resta quella che è e la lancetta gira, ad esempio, fino alle ore 2 (dipende essenzialmente da quanto è vicino il rivelatore alla superficie).

Il prodotto delle frecce ci dice che l’ampiezza finale è 1 x 0.98 x 1 = 0.98; la rotazione finale è 5 + 2 = 7.  La probabilità di questa strada complementare a quella della riflessione è, quindi, 0.98 ² = 0.96, ossia il 96%.

Non ci meravigliamo certo che la somma delle due probabilità sia proprio uguale al 100% (erano le sole due vie possibili).

Attenzione, però, a non cercare di combinare le ampiezze dei due percorsi per ottenere quella finale del 100% con il metodo della somma dei vettori! Questo si può fare solo se le vie alternative portano allo stesso rilevatore e non a due diversi. Anzi, ancora meglio, le due vie non sono vie alternative di un solo evento, ma sono vie che si riferiscono a eventi del tutto diversi. Mi raccomando…

Continuiamo a esercitarci con la moltiplicazione delle frecce di probabilità, scomponendo gli eventi che già conosciamo in vari passi. Dobbiamo acquistare una grande dimestichezza: le frecce devono diventare come il pane quotidiano…

Doppia riflessione

Riprendiamo, allora, la doppia riflessione sulla lastra di vetro e vediamo di sezionarla in vari passi, adottando la moltiplicazione appena descritta. Ancora una volta, ricordo che stiamo semplificando la situazione considerando solo la traiettoria di massima probabilità, senza tener conto della dispersione della luce. In questo caso, siamo interessati a vedere come la luce della sorgente arriva a uno stesso rilevatore, percorrendo due strade alternative. Alla fine, quindi, si dovranno, comunque, sommare le probabilità ottenute attraverso le due riflessioni.

La prima strada è esattamente uguale a quella descritta nella riflessione semplice. Non la ripetiamo di certo, a parte ricordare il risultato: ampiezza di probabilità uguale a 0.2.

Dividiamo in vari passi, invece, la riflessione che avviene nella seconda superficie. Ne abbiamo considerati sette e li rappresentiamo in Fig. 38  In particolare: (1) tragitto dalla sorgente al vetro; (2) passaggio da aria a vetro; (3) tragitto dentro al vetro da una superficie all’altra; (4) riflessione nella superficie posteriore; (5) nuovamente, il tragitto dentro al vetro, eseguito al contrario; (6) passaggio da vetro ad aria; (7) tragitto dal vetro al rivelatore.

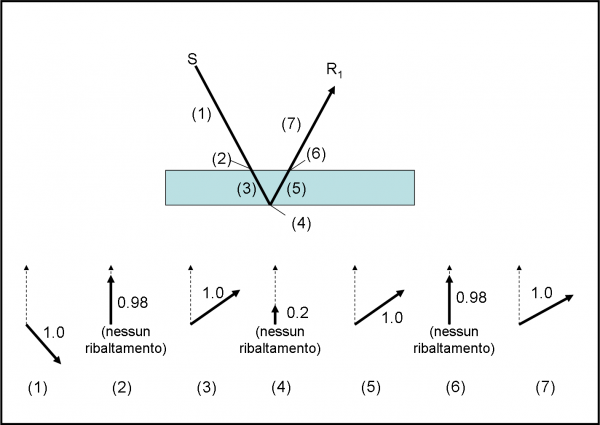
Sappiamo già bene che cosa succede per quasi tutti i passi. Dobbiamo solo aggiungere che la riflessione all’interno del vetro non comporta nessun cambiamento di verso alla freccia. Descriviamo, allora, punto per punto cosa succede. Tra sorgente e vetro non vi è, ovviamente, nessun accorciamento. Il passaggio da aria a vetro comporta, come già sappiamo, un accorciamento di 0.98, ma nessuna rotazione. Il tragitto nel vetro lascia tutto inalterato, tranne la rotazione della lancetta, mentre la riflessione nel vetro origina un accorciamento della freccia pari a 0.2, ma nessuna rotazione. Il ritorno nel vetro lascia inalterata la lunghezza della freccia e fa ruotare la lancetta della stessa quantità che si era trovata nel viaggio di andata (lo spessore della lastra è quello che è). Tuttavia, di quanto giri la freccia, ci importa relativamente poco, per il momento, dato che dipende dallo spessore della lastra.

Più interessante è calcolare l’ampiezza finale che è data dal prodotto dei vari “accorciamenti”. Esso risulta: 1 x 0.98 x 1 x 0.2 x 1 x 0.98 x 1 = 0. 192, che all’inizio di tutto avevamo già approssimato a 0.2. La combinazione con l’altra freccia di 0.2 (prima riflessione) dà un’ampiezza finale che varia da 0 a 0.4 e, quindi, una probabilità che varia da 0 a 0.16 (dallo 0% al 16%), a seconda dello spessore della lastra e, quindi, della rotazione della lancetta all’interno del vetro.

Riassumendo abbiamo stabilito che:

1) una riflessione aria-aria (prima superficie) riduce la freccia unitaria a 0.2 e causa una rotazione di mezzo giro.

2) una riflessione  vetro-vetro (seconda superficie) riduce la freccia unitaria a 0.2 ma non causa nessuna rotazione.

2) un passaggio aria-vetro o vetro-aria riduce la freccia a 0.98.

Siamo come San Tommaso

A questo punto, poniamoci una domanda che non ci eravamo fatti e che sembrerebbe veramente banale: “Cosa registriamo se poniamo un rivelatore al di sotto  della lamina?”. Il percorso è indicato in Fig. 39. Come fatto precedentemente per la semplice riflessione, stiamo confrontando due strade complementari (arrivano a diversi rivelatori), il cui risultato finale non deve portare a combinazione di frecce, ma all’ovvio fatto che la somma delle probabilità legate alle due possibilità DEVE essere 100%. Il fotone o sceglie una strada oppure l’altra: non c’è altra possibilità, per quanto abbiamo assunto fin dall’inizio della moltiplicazione. In parole veramente  “pratiche”: “Se su R₁ la probabilità è del 6%, ad esempio, su R₂ deve essere per forza 100% - 6% = 94%”.

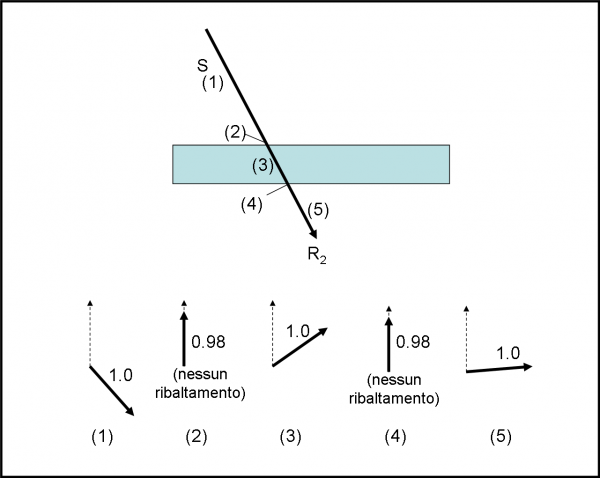
Noi, però, sappiamo che la probabilità di arrivare su R₁ (con due riflessioni) varia tra 0 e 16% e, di conseguenza, la probabilità che la luce arrivi su R₂ deve variare tra il 100% e l’84%.

Tuttavia, la QED ci ha abituato a risultati imprevisti e assurdi e quindi vale la pena calcolare passo per passo la storia della freccia che porta al secondo rivelatore, dato che ormai le regole le conosciamo molto bene. Già il fatto che il percorso sia uno solo comincia a crearci una certa agitazione…

L’evento si scompone in cinque passi: (1) da S alla lastra di vetro; (2) l’attraversamento della superficie  (aria-vetro); (3) tragitto all’interno della lastra di vetro; (4) attraversamento della seconda superficie (vetro-aria); (5) dalla lastra al rivelatore R₂.

Ci vuole poco a calcolare, attraverso il prodotto, l’accorciamento totale della freccia: 1 x 0.98 x 1 x 0.98 x 1 = 0.96

La direzione finale è la rotazione della lancetta senza interruzioni, dalla partenza all’arrivo, dato che non vi sono ribaltamenti.

Più assurdo dell’assurdo

Attenzione, adesso! Come previsto, la QED ci mostra uno dei suoi giochi di prestigio. Indipendentemente dallo spessore della lastra di vetro (che comporta solo diversi valori della probabilità finale di arrivare in R₁), la probabilità di arrivare in R₂ è sempre la stessa (cambia solo il tempo impiegato, ma poco importa dato che NON dobbiamo sommare questa freccia con quella relativa a R₁).

Ripeto ancora il risultato dato che sembra veramente assurdo, benché si parli di QED: l’ampiezza di probabilità, su R₂, è 0.96 e rimane sempre la stessa per qualsiasi spessore. Ciò comporta una probabilità di giungere in R₂ pari a 0.96² = 0.92. In  altre parole, più terra-terra, su 100 fotoni che partono da S, 92 arrivano SEMPRE su R₂. Su R1, allora, ne dovrebbero arrivare SEMPRE 100 – 92 = 8!

Accidenti, proprio quell’8% che ci saremmo aspettati prima di iniziare a divertirci a combinare le frecce. Eppure sappiamo benissimo, ormai, che la probabilità di giungere su R₁ varia tra 0% e 16%, a seconda dello spessore, passando solo due volte attraverso il valore dell’8%, proprio come ci ha dimostrato la Fig. 3.

C’è proprio qualcosa che non va. Facciamo un conto da scuola elementare per essere sicuri di non farneticare. Ammettiamo che su R₁ arrivi lo 0% (sappiamo che può benissimo succedere). Adesso sommiamo questo numero a quello trovato su R₂ (che non cambia mai, dato che vi è un solo percorso per arrivarci). Otteniamo 0% + 92% = 92%.... Accidenti, ci siamo persi per strada un 8% di fotoni. Dove sono scappati?

Ma la situazione è ancora più drammatica se, come deve capitare senza alcun dubbio, in R₁ arrivano ben 16 fotoni, ossia se la probabilità è del 16%. La somma delle due probabilità complementari è : 16% + 92% = 108%. Di male in peggio… adesso abbiamo addirittura superato il 100%, come se arrivassero nuovi fotoni dal nulla. Ve bene che la QED è assurda, ma qui si esagera!

Viene da pensare che la freccia o ampiezza di probabilità e il suo modo di calcolarla siano delle grandi fesserie… Eppure ci hanno permesso di calcolare molti eventi legati alla luce, anzi –se crediamo a Feynman- TUTTI.

Un’assurdità dovuta a una visione parziale

Mamma mia, che sciocchi che siamo! Non abbiamo considerate TUTTE le strade che un fotone può compiere per andare da S a R₂. Infatti, ve n’è un’altra che non possiamo certo trascurare ed è rappresentata nella Fig. 40. Essa ci dice che il fotone può riflettersi nuovamente sulla superficie superiore (dalla parte del vetro, però!), tornare indietro, attraversare la seconda superficie e arrivare nuovamente in R₂. Questa volta dobbiamo considerare ben nove passi.

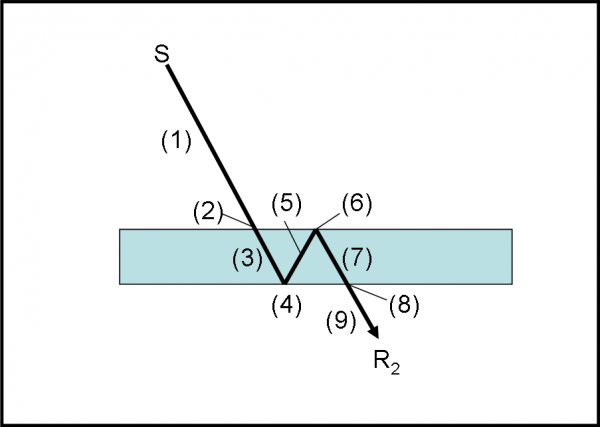
No, non spaventatevi! In fondo è solo questione di accorciamenti e di rotazioni. Quali sono i passi che accorciano la freccia? Sono (2), (4), (6) e (8). Il primo riduce a 0.98, il secondo a 0.2, il terzo a 0.2 e il quarto ancora a 0.98. Moltiplichiamo e otteniamo 0.98 x 0.0.2 x 0.2 x 0.98 = 0.0384, che possiamo approssimare con 0.04. Questa è un’ampiezza di probabilità di un percorso alternativo a quello precedente che  arrivava anch’esso su R₂. Le due frecce o ampiezze di probabilità vanno quindi COMBINATE assieme! Ma la loro combinazione dipende molto dalla direzione delle due frecce da combinare…

Finora non ci eravamo curati della lancetta del cronometro, ma adesso diventa necessario per poter calcolare la vera probabilità che un fotone ha di giungere in R₂. Quanto giri la lancetta nelle due vie alternative legate a R₂ dipende sicuramente dallo spessore della lastra, così come dipendevano dallo spessore le ampiezze che si combinavano in R₁.

Tuttavia, il problema si risolve in modo generale con un ragionamento veramente semplice che è sintetizzato nella Fig. 41.  Permettiamoci, per semplicità di figura, di far ruotare solo la freccia senza curarci della lunghezza, dato che come si accorcia l’abbiamo già calcolato precedentemente.

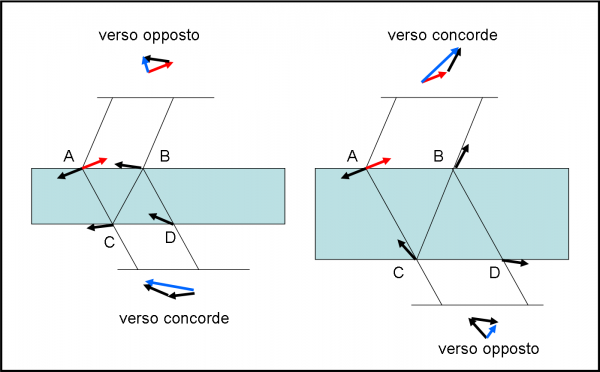
Trascuriamo anche alcuni tragitti che non servono alla soluzione finale. Innanzitutto quello da S ad A che non influenza assolutamente il discorso successivo. Ci dice solo come è diretta la freccia all’inizio della danza dentro alla lastra. Trascuriamo anche  i tragitti da A a R₁ e da B a R₁ così come quelli da C a R₂ e da D a R₂, dato che essi sono uguali, a due a due, per costruzione. La lancetta gira, infatti, dello stesso valore per entrambe le coppie di traiettorie.

Possiamo perciò esaminare la freccia solo nella parte “interna” alla lastra. Domandiamoci: “Quale tragitto, nel vetro, determina la direzione della freccia che si ottiene in B?” Beh… facilissimo: ACB. Non vi è infatti nessuna inversione di direzione in C dato che è riflessione vetro-vetro. Possiamo dire che la direzione della freccia in B può essere diretta comunque rispetto a quella in A, ma questa differenza è solo dovuta allo spessore della lastra.

Nella prima situazione intermedia (parte sinistra della figura), lo spessore è piccolo e la freccia “nera” da A a C e, quindi anche da C a B, ruota solo di 15° (ad esempio). In B quindi si ha una rotazione di 30° rispetto a quella di A. Tuttavia, attenzione! La freccia che non entra nel vetro e viene riflessa direttamente verso R₁ DEVE essere ribaltata rispetto a quella che entra, ossia diventa la freccia “rossa”. In R₁, quindi, qualsiasi sia il tragitto AR₁ = BR1, si devono combinare due frecce che hanno verso quasi opposto (angolo tra loro ben maggiore di 90°) e la cui somma vettoriale si riduce (diventa zero solo se la direzione è esattamente la stessa).

Cosa capita alle frecce che vanno verso R₂? Una è quella in C e l’altra è quella in D. Il tragitto CBD, però, è esattamente uguale ad ACB. Se quest’ultimo ha ruotato la lancetta di 15° + 15° = 30°, lo stesso deve fare anche la freccia che va da C a D. Anche la riflessione in B è vetro-vetro e quindi non comporta inversione di lancetta. Questa volta, la freccia in C si somma vettorialmente alla freccia in D senza subire alcuna inversione: nera è e nera rimane. Ha subito due riflessioni (in C e in B) ma entrambe del tipo vetro-vetro. In R₂, dobbiamo, quindi, combinare due frecce che hanno verso quasi concorde (angolo ben minore di 90°), la cui ampiezza di probabilità finale aumenta. Esattamente il contrario di quanto capita in R₁. Nel caso in cui la direzione è esattamente la stessa, otteniamo la massima lunghezza possibile.

Aumentiamo, adesso, lo spessore (parte destra della figura). Tutto rimane lo stesso, ma la freccia che entra in A gira molto di più prima di arrivare in C. Ad esempio, di 70°. La freccia arriva quindi in B avendo girato di 70° + 70° = 140°. La freccia rossa e quella nera che vanno verso R₁ hanno adesso verso quasi concorde e la loro somma vettoriale aumenta l’ampiezza fino a farla diventare massima se la direzione è la stessa. Dato che il percorso ACB è lo stesso di CBD, anche la freccia che esce in D ruota di 140° rispetto a quella di C. Dato che non hanno subito ribaltamenti esse hanno, questa volta, versi quasi opposti e la freccia finale si riduce, diventano minima quando la direzione è proprio uguale. Attenzione: in questo caso non si annulla l’ampiezza, dato che queste due frecce hanno lunghezza nettamente diversa (0.92 e 0.04) come abbiamo visto precedentemente.

Insomma, quando in R₁ aumenta l’ampiezza, in R₂ si riduce e viceversa. Proprio quello che volevamo!

Tradotto in numeri (ossia, considerando anche le ampiezze e non solo la lancetta), questo procedimento ci porta, nei casi limite, alle seguenti conclusioni:

(a) Se in  R₁ sommiamo due frecce entrambe di 0.2 si ha un’ampiezza finale di 0.4 che porta a una probabilità del 16%. In R₂ avviene, allora, il contrario. A un’ampiezza di 0.96 si deve togliere un’ampiezza di 0.04, ottenendo 0.92. il cui quadrato (ossia la probabilità finale) diventa proprio 0.84, ossia l’84%. Le cose funzionano perfettamente, dato che 16% + 84% = 100%. I cento fotoni partiti da S  non sono aumentati lungo la strada!

(b) Se in R₁ sottraiamo due frecce entrambe di 0.2 si ha un’ampiezza finale di 0 che porta a una probabilità dello 0%. In R₂, avviene il contrario e le frecce si devono sommare. Ossia: 0.96 + 0.04 = 1.00 (ricordiamo sempre che la somma vettoriale in questi casi limite si riduce alla somma aritmetica). La probabilità in R₂ diventa, perciò del 100%. Mi posso permettere di dire che 0% + 100% = 100%. Ancora una volta tutto torna e i famosi fotoni persi per strada non esistono assolutamente. Tutti e 100 arrivano a destinazione.

ESERCIZIO PER I PIU’ ABILI (ma risolvibile da tutti)

Volete vedere se avete capito questa parte un po’ più ardua del solito? Disegnate le frecce nei punti A, B, C e D, nel caso intermedio in cui la probabilità di R₁ è l’8% , verificando che in R₂ si trova una probabilità del 92%. Tutto l’esercizio sta nel disegnare la rotazione giusta della freccia da A a B e, quindi, da C a D… Analogamente, potete disegnare, molto facilmente, anche i casi limite che abbiamo descritto a parole.

Nessuna approssimazione nella QED

Un’ulteriore considerazione estremamente importante. Avrete notato che ogni tanto abbiamo eseguito delle approssimazioni… Un valore di 0.038 l’abbiamo preso uguale a 0.04, ma prima ancora avevamo detto che si poteva approssimare 0.192 con 0.2. Non solo, però…i vari quadrati sono stati spesso tagliati “brutalmente” nelle loro cifre decimali.

Ma come? Una rappresentazione esatta e perfetta come la QED è costretta a eseguire approssimazioni per far tornare le percentuali? Accidenti, siamo mal messi. No, no, cari amici, la QED è l’unica strategia operativa che riesce a determinare perfettamente certe costanti della fisica fino a decimali sempre più lontani dalla virgola. Anzi, può riuscire ad arrivare fino alle dimensioni minime della fisica, se no che “quantistica” sarebbe?

Faccio in fretta a rispondervi. Basta la Fig. 42,  in cui abbiamo aggiunto una nuova riflessione sulla seconda superficie. In R₁ arriva un’ulteriore freccia di ampiezza molto piccola (0.008) che deve combinarsi con quelle precedenti… E che dire se aggiungiamo ancora un’altra riflessione vetro-vetro sulla prima superficie e facciamo uscire il fotone dalla superficie inferiore? Un’altra freccia piccola piccola si combina a quelle precedenti e via dicendo… Insomma, possiamo continuare a far riflettere il fotone dentro al vetro e farlo uscire un po’ sopra e un po’ sotto in modo da ottenere frecce sempre più piccole che si combinano a quelle già trovate sia su R₁ che su  R₂.

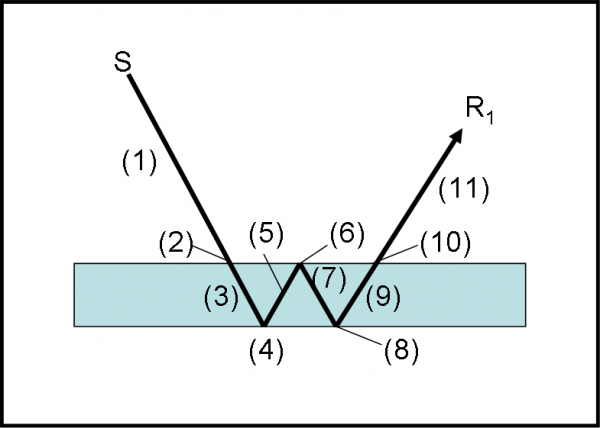
ALTRO ESERCIZIO (molto utile)

Potete facilmente, lavorando con calma e pazienza, calcolare la combinazione finale di un percorso come quello appena descritto (e anche quelli successivi). In fondo, basta moltiplicare tra loro gli “accorciamenti” subiti secondo le poche regole imparate finora. Toccherete con mano la continua diminuzione dell’ampiezza delle frecce aggiuntive…  E’ inutile pensare alla lancetta del cronometro: lei continua a percorrere percorsi uguali e il risultato finale non cambia rispetto al caso descritto precedentemente. Le freccette continuano a sommarsi o a sottrarsi a seconda dello spessore della lastra.

Continuando in questa danza ripetitiva, stiamo tranquilli che lo 0.038 diventerà lentamente sempre più uno 0.40 seguito da tanti, tanti zeri! E lo stesso succede per  0.192 che diventa veramente 0.2. Una serie di  trasmissioni e riflessioni che non terminano teoricamente mai. Così come capita nell’arcobaleno: a volte se ne riescono a vedere due, ma, teoricamente, ne potremmo vedere molti di più…

Beh… è stata una descrizione abbastanza “dura”  e possiamo rifiatare un po'. Capisco benissimo che a qualcuno sarà apparso un inutile gioco geometrico e matematico. E, forse, inizierà a pensare che è molto meglio tornare all’ottica geometrica. In fondo, si trovano le stesse cose senza tante frecce e lancette che si accorciano, girano si sommano e si sottraggono. Vi prego di non farlo! Tra non molto, questo assurdo comportamento del fotone si scontrerà con la materia e le cose diventeranno molto più concrete!

Per affrontare meglio questo concetto ci serve  un’ulteriore applicazione della moltiplicazione di ampiezze di probabilità (ossia le ben note frecce).  Finora, abbiamo detto che questo procedimento si applica per descrivere come “evolve” la freccia di probabilità durante i passi successivi in cui può essere scomposto un evento.

Uno o l’altro per me pari sono

La regola della moltiplicazione si applica, però, anche a un evento che consiste di “cose” che accadono in concomitanza, indipendentemente tra loro e magari nello stesso momento.

Passiamo subito a un esempio: supponiamo di avere due sorgenti X e Y e due rivelatori A e B. Vogliamo calcolare la probabilità di un evento così definito: dopo che un fotone è uscito da X e uno da Y, sia A che B vengono raggiunti da un fotone. I due fotoni non si riflettono né attraversano qualche mezzo diverso. No, vanno senza problemi dove vogliono o -meglio- possono. Per studiare questo evento, che sembrerebbe di una banalità irrisoria, possiamo smettere di fare semplificazioni come quelle usate per la riflessione semplice o doppia, dove avevamo considerato solo una traiettoria, quella in qualche modo più probabile. Adesso, consideriamo veramente il fotone come un qualcosa che può andare ovunque (pur limitandoci alle linee rette, dato che sappiamo perché si può fare). Sembra una cosa semplice, ma finalmente affronteremo di petto la vera essenza del fotone e della QED. Un fotone esce da X e un fotone esce da Y, ma entrambi hanno a disposizione l’intero spazio e niente può disturbarli prima di arrivare (se arrivano) in A e B.

Se continuassimo a confondere una singola traiettoria con un singolo fotone, potremmo dire con grande sicurezza: l’evento capita sempre! Infatti, vi è sempre almeno un fotone che va da X ad A e uno che va da Y a B. L’errore di questo ragionamento è pensare che per ogni traiettoria esista un fotone. Invece, la situazione è ben diversa concettualmente: ogni traiettoria è un possibile percorso di un singolo fotone, ossia esso può trovarsi in una qualsiasi di esse, con una certa ampiezza di probabilità. In queste condizioni non è così sicuro che i due fotoni lanciati da X e Y debbano veramente arrivare su A e B o –quantomeno- molto dipende da “come” ci arrivano. In altre parole, studiamo la probabilità di arrivarci.

L’evento deve tener conto sia del fotone di X che di quello di Y. In altre parole, i fotoni che partono da X e Y non sono mai veramente indipendenti ai fini dell’evento. L’evento ci dice, in fatti, che sia il fotone di X sia quello di Y devono arrivare a destinazione e quindi è giusto e “logico” adottare la regola della moltiplicazione.

Spieghiamo meglio le cose attraverso la semplicissima Fig. 43. Prima di farlo, però, indichiamo con esattezza e senza alcuna semplificazione, cosa è necessario e sufficiente conoscere per rappresentare la luce che esce da una sorgente: (1) l’angolo della freccia segnato dalla lancetta del cronometro che gira in relazione al colore della luce; (2) la lunghezza della freccia che, però, dobbiamo considerare variabile NON perché incontra qualche ostacolo, ma solo perché percorre uno spazio crescente.

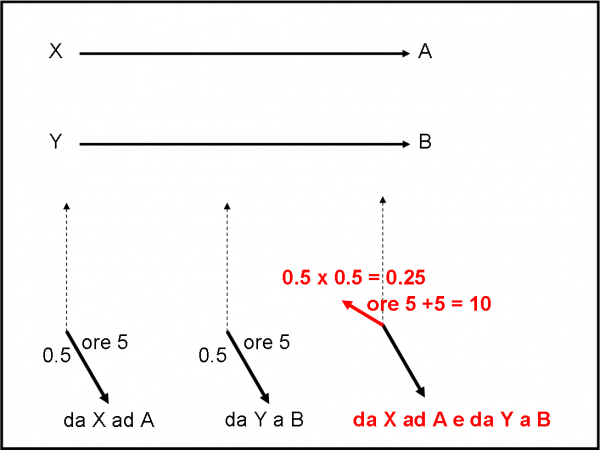
La seconda caratteristica ci è nuova, dato che finora non aveva importanza per i fenomeni studiati. Per essere pronti a entrare nel mondo della materia, però, non possiamo più trascurarla. In particolare, la lunghezza della freccia, ossia l’ampiezza della probabilità che il fotone ha di viaggiare su quella traiettoria, è inversamente proporzionale alla distanza dalla sorgente. Questa regola si traduce facilmente nella nozione che tutti abbiamo imparato a scuola e che dice: “l’intensità della luce emessa da una stella o da una sorgente qualsiasi diminuisce con il quadrato della distanza”. Nella QED la probabilità è proprio il quadrato dell’ampiezza di probabilità e quindi la probabilità diminuisce con il quadrato della distanza. Questa è la vera regola della Natura… Possiamo quindi applicare la nuova regola, sapendo che è verificata in Natura.

Torniamo allora al nostro evento di Fig. 43 e assumiamo, ad esempio, che la lunghezza della freccia alla distanza A da X si sia ridotta a 0.5. Assumiamo anche che la lancetta si fermi sulle ore 5. La stessa identica cosa succede per il tragitto YB. Anche la freccia relativa alla luce di Y che giunge in B si è ridotta a 0.5 e la lancetta segna le 5. La luce è monocromatica e le distanze XA e YB sono identiche. Posso concludere che la probabilità dell’evento è il 100%? Assolutamente no, dato che, come già ripetuto fin troppe volte, la traiettoria ha una freccia con una certa probabilità, che abbiamo appena calcolato. Bene, per conoscere la probabilità finale dell’evento dobbiamo moltiplicare tra loro le due frecce. Il metodo lo conosciamo bene: si moltiplicano “aritmeticamente” le ampiezze e si sommano le rotazioni della lancetta dei due percorsi. In conclusione, l’ampiezza di  probabilità (la freccia) finale dell’evento è dato da 0.5 x 0.5 = 0.25 e la sua direzione segna le ore 10.

Attenzione: non devo sommare vettorialmente le due frecce, dato che non sono vie alternative (o una o l’altra), ma sono proprio strade indipendenti che portano ognuna al “successo” di una parte dell’evento. In questa ottica, è proprio come se fossero passi successivi di un singolo evento.

Ma siamo sicuri di avere agito bene? Non ci siamo, forse, dimenticati qualcosa? Direi proprio di sì. Quella descritta è solo una delle vie possibili perché si verifichi l’evento. Ne esiste, infatti, un’altra: il fotone di X può raggiungere B e quello di Y può raggiungere A. Nessuno lo vieta, dato che il fotone è descritto da tutte le sue possibili traiettorie. In parole povere, può capitare la situazione di Fig. 44.

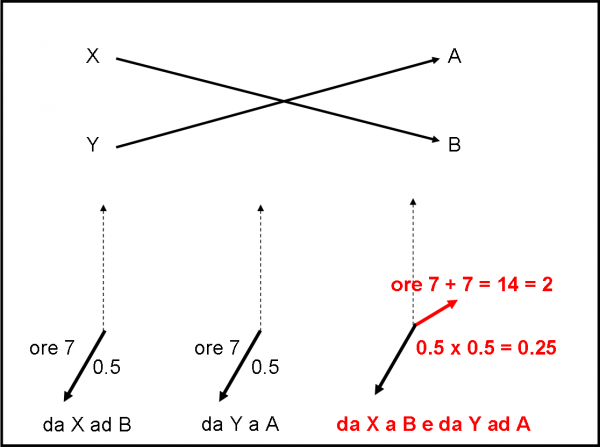
A questo punto dobbiamo fare una riflessione (mentale... non sul vetro!). Le distanze XA e XB (così come YA e YB) sono veramente molto simili, quasi perfettamente uguali (la sorgente è molto distante dai rivelatori). Possiamo quindi tranquillamente dire che restano invariate nella via alternativa che dà luogo all’evento. Ciò vuole anche dire che le relative ampiezze di probabilità (le frecce) hanno anche loro un valore di 0.5. Non possiamo, invece, dire lo stesso per la lancetta del cronometro. Anche una piccolissima differenza di distanza fa girare notevolmente la lancetta. Ricordiamoci, infatti, che essa compie 1.440.000 giri per ogni metro. Ne segue che anche una infinitesima variazione di distanza fa variare la direzione della lancetta in modo significativo (un po’ quello che succedeva con lo spessore della lastra di vetro…).

Ne consegue che la seconda via per verificare l’evento comporta una freccia finale di pari ampiezza di quella precedente (0.5 x 0.5 = 0.25), ma con una direzione diversa. A questo punto abbiamo due strade alternative per verificare l’evento. Due strade alternative vogliono dire che dobbiamo combinare le due frecce finali (ottenute con la moltiplicazione) attraverso la somma vettoriale, come illustrato in  Fig. 45.

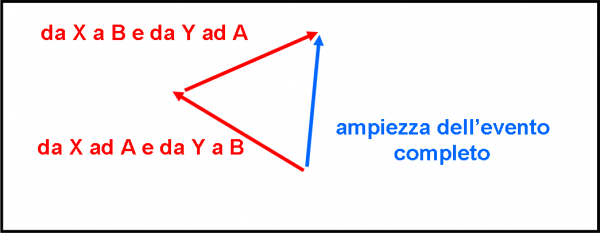
Basta variare di poco la distanza relativa di A e B  o di X e Y (spostando un poco un rivelatore o una sorgente o quello che preferite) e cambiano anche le direzioni delle due frecce ottenute con la moltiplicazione. La somma vettoriale può quindi portare al caso che le due frecce siano perfettamente concordi o perfettamente opposte. Analogamente al caso della doppia riflessione, possiamo, quindi, amplificare al massimo la probabilità finale o annullarla del tutto.

Questo fenomeno, che sembra un po’ troppo teorico, a prima vista, ha un suo nome: effetto Hanbury-Brown-Twiss e permette, spostando adeguatamente i rivelatori, di distinguere tra una radio sorgente singola e una doppia, anche quando le due sorgenti sono estremamente vicine tra loro. Non ci vuole molta fatica per dire che siamo di fronte a un fenomeno di interferenza...

Qualcuno potrebbe pensare che abbiamo considerato solo traiettorie rettilinee e quindi due sole alternative.  Ormai sappiamo bene perché si possono considerare solo loro per rappresentare tutte le traiettorie possibili. In ogni modo, non vi è nessun problema. Si potrebbero anche disegnare tutte le traiettorie più strambe che possono verificare l’evento che stiamo analizzando. Il succo non cambierebbe. Possiamo stare tranquilli che le traiettorie strambe darebbero luogo a frecce che girano in tondo e servirebbero ben poco alla probabilità finale!

Ricordiamo, però, sempre, che la freccia finale NON è associata a un fotone, ma all’ampiezza di probabilità della riuscita di un evento. Un fotone parte, fa qualcosa e arriva a destinazione: che probabilità ha di riuscirsi?

Cari amici, alla QED non la si fa… ha una risposta a tutto e sa descrivere come nessuno la Natura. Peccato che non si riesca a capirne le regole…

Aspettando la materia

Prima di iniziare il passo successivo verso la materia, mi sembra doveroso parlare del celebre esperimento della doppia fenditura che è uno dei capolavori di Richard. Chi ha letto la descrizione che ne avevo dato a suo tempo (vedi Introduzione alla MQ nella sezione Approfondimenti), si ricorderà che era  stata un’esposizione abbastanza faticosa, in quanto si era partiti da una visione “normale” delle caratteristiche della luce e, quindi, la contrapposizione particella-onda sembrava veramente un’assurdità senza speranza. Adesso, che abbiamo “capito” come funzionano le regole della QED, vedremo che diventa quasi un gioco da ragazzi, privo di vere difficoltà. Anzi, ci meraviglieremmo se le cose non funzionassero così.

Non solo però, e qui sta la parte più importante dell’esperimento. Saremo anche in grado di “spiegare” tecnicamente perché guardando o -meglio- rilevando il punto di passaggio di un fotone attraverso un foro, il fenomeno d’interferenza scompare. Per fare questo è fondamentale saper definire esattamente un evento e non mischiare tra loro eventi completamente diversi. Le tante parole precedenti sono proprio servite a questo.

Rileggete ancora una volta come si definisce un evento e quali caratteristiche deve avere, tenendo conto che una cosa è sommare vettorialmente due ampiezze (strade alternative per ottenere uno stesso evento), un’altra è moltiplicare le ampiezze (passi intermedi di un evento o passi indipendenti che fanno comunque parte di un solo evento), e un’altra ancora è sommare “normalmente” le probabilità finali (due eventi del tutto separati… ricordatevi la luce che può essere riflessa su R₁ o rifratta su R_2, nella lastra di vetro).

Dopo l'applicazione alla doppia fenditura, faremo veramente entrare in scena gli altri attori. Apriremo la porta che ci introduce all’interazione dei fotoni (e delle loro assurde caratteristiche) con la materia (composta anch’essa da particelle…). Finalmente “capiremo” il perché di certi atti di fede, come l’ampiezza 0.2 della riflessione, il rallentamento subito passando dall’aria al vetro o all’acqua, e via dicendo.  Anzi, capiremo che i fotoni fanno ben poco! Vedremo che non sono loro che si riflettono o attraversano una superficie. No, loro danno solo degli “ordini”. In parole più “tecniche”, i fotoni si spostano solo da un elettrone a un altro. Tocca a questi ultimi catturare e riemettere i fotoni che li colpiscono. Insomma, l’attraversamento e la riflessione sono in realtà operazioni che compiono gli elettroni, i veri “manovali” delle interazioni luce-materia. Vedremo anche che ci verrà utile il concetto di spaziotempo descritto dal cono di luce (su cui ho sempre battuto “duramente”).

Insomma, ne vedremo proprio delle belle!

P.S. Volevo aggiungere un’annotazione. Vi sarete resi conto che certi concetti base li ho ripetuti quasi in ogni articolo. Forse, qualcuno avrà anche “sbuffato”: “Basta, abbiamo capito!”. Tuttavia, ho pensato che il richiamare quasi costantemente a cosa stiamo realmente applicando la QED fosse troppo importate per non tenerlo sempre a mente, rischiando di perderlo di vista… Ormai mi conoscete e mi dovete accettare con tutte le fissazioni e ripetizioni… Sto per ripetermi anche adesso!

Con tutto quello che abbiamo imparato finora (soprattutto, le regole di calcolo della probabilità di un evento attraverso le frecce associate alle traiettorie percorribili da un fotone), non è  difficile riprendere il celebre esperimento della doppia fenditura, su cui tanto a lungo abbiamo discusso, e descriverlo con grande naturalezza. Ci sembrerà più che ovvio. Addirittura, tenendo conto della separazione degli eventi in passi successivi, si può anche dare una risposta alla parte più assurda, ossia quella relativa al guardare o non guardare da dove passa il fotone. Vale proprio la pena descriverlo nuovamente, cercando di afferrare bene non tanto le operazioni (ormai banali) ma i concetti che ne derivano, soprattutto l’ultimo.

Prepariamo l’esperimento con la sorgente S e la parete con i due fori A e B, distanti tra loro pochi millimetri, e il rivelatore R. Poniamo il foro A proprio nella direzione SR (ma potevamo anche cambiare la posizione dei fori).  La cosa veramente importante è che i fori siano molto piccoli. Perché? Dovreste ricordarvelo: se i fori sono piccoli le traiettorie che li attraversano danno luogo a una combinazione delle  frecce di ampiezza comparabile, indipendentemente dalla lunghezza della traiettoria seguita e dal tempo impiegato a percorrerla. In altre parole, la traiettoria SAR  ha la stessa probabilità finale di SBR, malgrado la seconda sia decisamente più lunga. Ricordiamo, per avere un’idea più chiara delle grandezze in gioco, che se i due fori distassero un metro, il loro diametro dovrebbe essere di un decimo di millimetro…

Partendo da questa verità, non è quindi difficile superare la prima apparente assurdità della situazione: se chiudo A ottengo un certo risultato su R. Se chiudo B ottengo lo stesso identico risultato. In numeri (come esempio): se S invia cento fotoni, uno solo passa attraverso A (con B chiuso) e arriva su R (facendo “tic”). Se chiudo A, e mando altri cento fotoni, R farà nuovamente “tic” una sola volta, confermandoci che il percorso SBR ha la stessa probabilità di SAR. Questo è un risultato già abbastanza assurdo per la vita normale, ma sappiamo spiegarlo benissimo con un fascio di traiettorie molto strette.

Accettiamo quindi che la probabilità di arrivare su R da S, sia attraverso A che B, sia la stessa, ad esempio l’1%. Apriamo, ora, entrambi fori. Se ragionassimo come siamo abituati a fare, dovremmo dire che, se lanciamo 100 fotoni da S, ne arrivano 2 su R: uno attraverso A e uno attraverso B. Questa è la nostra logica. Chi non ha letto quanto scritto finora si stupirebbe non poco del fatto che, invece, il numero di fotoni che giunge su R varia da un valore minimo di zero a uno massimo di 4.

Noi, però, siamo già abbastanza preparati da sapere che non possiamo sommare le probabilità nel modo più banale, ossia 1 + 1 = 2! Qual è l’evento che devo studiare? Il fotone parte da S e arriva in R con due percorsi alternativi (esso è verificato sia se il fotone passa da A sia se passa da B). Alternativi? Ma allora sappiamo benissimo come fare: dobbiamo disegnare le ampiezze di probabilità per le due traiettorie possibili (attraverso A e attraverso B), fare girare il cronometro, che gira di più per il percorso più lungo, e sommarle vettorialmente. La probabilità finale è il quadrato dell’ampiezza finale.

Tutto dipende, quindi, dalla distanza tra i fori, ossia dalla differenza di percorso effettuato nelle due traiettorie alternative, ossia, da quanto ha girato la lancetta nei due casi. Per una certa distanza tra i fori potremmo avere che le due frecce vanno nello stesso verso e quindi prima sommiamo le frecce: 1 + 1 = 2 e poi eseguiamo il quadrato, che mi dà una probabilità finale di 4 (il 4%). Per un’altra distanza tra i fori, potremmo avere che le due frecce vanno in verso opposto, ossia 1- 1 = 0, il cui quadrato resta 0 (lo 0%).

E’ la stessa cosa che abbiamo trovato con la doppia riflessione sulla lastra di vetro sul rivelatore R1, niente di più e niente di meno. Non sappiamo assolutamente perché il fotone decida di passare da A o da B, ma sappiamo benissimo calcolare la probabilità di ogni traiettoria possibile del singolo fotone e combinarle in modo da ottenere la probabilità finale dell’evento.

Ovviamente, invece di spostare i fori, potremmo spostare il rivelatore R e troveremmo che, mentre si muove, la luce passa da un massimo (4%) a un minimo (0%), in relazione alla rotazione della lancetta, ossia alla distanza totale percorsa nelle due strade alternative. Questo fenomeno, che sappiamo trattare benissimo con le nostre frecce, è seguito pari pari dalla Natura e viene chiamato “normalmente” interferenza.

Quanto detto lo illustriamo in Fig. 46

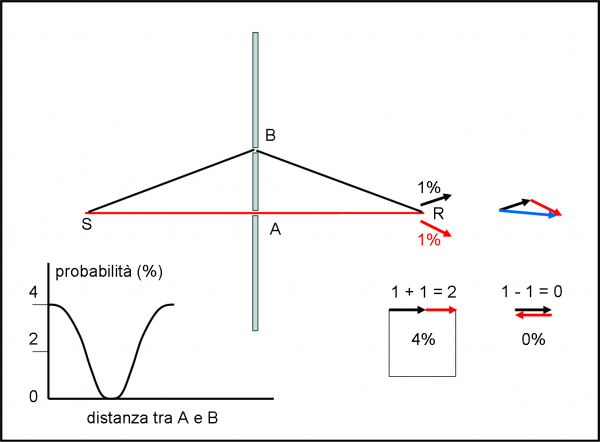
Se, invece, apriamo uno alla volta i fori, abbiamo due eventi separati: uno che dice di andare da S a R attraverso A e un altro che dice di andare da S a R attraverso B. Non vi sono alternative e quindi la freccia che arriva in R è una e una sola per ogni evento. Chiudendo A e aprendo B, la sola traiettoria possibile è SBR. Chiudendo B, l’unica traiettoria possibile è SAR.  Non abbiamo un evento con due alternative, ma due eventi, ciascuno senza alternative. Non dobbiamo quindi sommare vettorialmente le frecce, ma sommare “brutalmente” le percentuali dei due eventi, così come abbiamo fatto sommando le percentuali trovate nel rivelatore che riceve la doppia riflessione e in quello che riceve la trasmissione attraverso la lamina di vetro.

Ogni evento ha, come già detto, la probabilità dell’1%. I due eventi sono separati e quindi se vogliamo sapere quanti fotoni arrivano su R, passando da A o da B, dobbiamo sommare “brutalmente” le due probabilità e otteniamo 1 + 1 = 2. Non andiamo contro la QED e la differenza del risultato dipende solo da come è definito l’evento. Impariamo bene questo concetto e analizziamo sempre con molta attenzione le caratteristiche dell’evento di cui vogliamo calcolare le probabilità di riuscita.

Esistono ancora problemi di comprensione tra il fatto che, quando il foro è singolo, il fotone si comporta come “vera” particella, e il fatto che, quando i fori sono due, il fotone si comporta come un’onda? Un’onda che nei due fori dà luogo a due onde che interferiscono tra loro. No, direi proprio di no. Ormai nella logica della QED questo è un risultato ovvio e comprensibilissimo.

E’ bastato pensare un fotone come un insieme di particelle virtuali che possono essere ovunque, o, meglio ancora, trattare il comportamento di un fotone come un insieme di traiettorie ognuna con la propria ampiezza di probabilità di soddisfare un certo evento

Se questo fatto non vi risulta banale e ovvio, vi consiglio di ricominciare da capo la QED… Ma spero che non capiti a nessuno!

Ridendo e scherzando abbiamo descritto l’interferenza e abbiamo visto perché dipende dalla separazione dei fori o dal punto in  cui si mette il rivelatore. Abbiamo dimostrato che le particelle (e i fotoni lo sono perché fanno “tic” sul rivelatore) vanno trattate attraverso ampiezze di probabilità per ottenere i risultati che segue la Natura. Nessuna vera dualità particella-onda, ma solo freccia e cronometro… Mi raccomando, stiamo sempre bene attenti a definire perfettamente l’evento!

Fin qui nessun problema direi… Il bello viene adesso. Comunque, vedremo che la QED riesce anche a spiegare “a modo suo” il famoso fotone dispettoso che diventa particella se lo guardi e rimane onda se non lo guardi. Ossia il nocciolo di fondo di tutta la MQ. E non lo fa assolutamente dando all’osservatore e al suo cervello una capacità miracolosa…

Proseguiamo allora con molta calma. L’esperimento rimane tale e quale a prima, ma adesso al posto dei fori A e B, usiamo due fori muniti di un rivelatore incorporato. Ossia un qualcosa che, in pratica, ci dice se il fotone passa attraverso quel foro. Non dobbiamo confonderci: noi trattiamo nella QED il fotone come un insieme di ampiezze di probabilità che, in questo senso, possono passare sia da A che da B e combinarsi assieme. Tuttavia, il fotone resta una particella e in  realtà o passa da A o passa da B, non può passare mezzo da A e mezzo da B o cose del genere. Quelli che arrivano in R devono essere passati da qualche parte come particelle. Siamo solo noi, che non sapendo come spiegare la scelta dei fotoni, li abbiamo trattati e descritti come ampiezze di probabilità. L’importante è che facendo così riusciamo a descrivere perfettamente la Natura!

Torniamo ai due fori “intelligenti” o -molto meglio- capaci di registrare in qualche modo se un fotone passa o no attraverso di lui (basta la tecnologia e non l’intelligenza…e già la MQ cambia un po’ la sua visione troppo legata all’uomo… ma ci torneremo sopra, ovviamente). Il risultato lo sappiamo bene: l’interferenza scompare e il rivelatore R si comporta come ci saremmo aspettati fin dall’inizio: 1 + 1 = 2 e non certo 0 oppure 4!

Una soluzione apparentemente e normalmente NORMALE che, adesso, non ci soddisfa più e ci mette in crisi! Se ci sta succedendo questo, vuol dire che siamo entrati nel mondo di Alice e stiamo pensando come lei: il normale diventa assurdo e l’assurdo diventa normale.

Non sembra, però, che vi sia nessuna regola descritta finora che possa spiegare questo strano comportamento. La normalità del risultato sta distruggendo le nostre certezze basate sulla QED. Ma ne siamo proprio sicuri? Come abbiamo già detto varie volte, dobbiamo essere sempre certi di aver definito perfettamente l’evento. Due eventi uguali devono dare risultati uguali. A noi sembra che aggiungere i fori “intelligenti” non abbia cambiato l’evento e, invece, è proprio così. Seguiamo bene il ragionamento perché è veramente fondamentale (anche se rispecchia pari pari quanto detto poche righe sopra)

Per essere sicuri che l’evento non sia cambiato dobbiamo analizzare molto bene le condizioni iniziali e finali in modo da accorgerci se esse sono variate. Se così fosse, tutto l’evento sarebbe stato modificato e il risultato potrebbe benissimo essere diverso.

Descriviamo bene l’evento senza fori “intelligenti”. Cosa dice esattamente? Molto semplice: la luce parte da S, può passare da A o da B, e il rivelatore R fa “tic”. L’unica variazione di condizioni che avviene durante l’esperimento è il “tic” del rivelatore. O lo fa o non lo fa. Noi non possiamo sapere come si è mossa effettivamente la luce e quindi la descrizione data dalla QED ci dimostra che vi deve essere interferenza e la Natura lo conferma.

Quando inseriamo i fori “intelligenti”, noi cambiamo profondamente l’evento che adesso diventa: la luce parte da S, A o B registrano il passaggio del fotone, il rivelatore R fa “tic”. Non ditemi che è la stessa cosa di prima! Vi sono ben tre condizioni: la registrazione effettuata del foro A, quella del foro B e il solito tic di R (che c’era anche prima). L’evento non è più lo stesso!

Questo evento è in realtà scomponibile in due eventi distinti e completi: (1) la luce parte da S, passa  da A e fa tic in R; (2) la luce parte da S, passa da B e fa tic in R. Due eventi completamente separati, che vanno trattati in modo diverso secondo le regole imparate.

Scomponiamo (1) in due passi: da S ad A e da A a R. Dobbiamo farlo per studiarlo adeguatamente perché in A cambiano le condizioni, così come capitava nell’esperimento della doppia riflessione e in altri esempi. La freccia che arriva in A deve essere MOLTIPLICATA con quella che va da A a R. Tuttavia, questo evento è perfettamente uguale a quello con solo A aperto. Il foro intelligente non cambia la probabilità finale, ma implica solo che l’evento completo (da S a R) deve essere spezzato in due eventi separati.

Ripetiamo ancora il concetto. L’evento che porta all’interferenza dice solo e soltanto: parti da S e arriva in R facendo “tic”. Esso, per come è formulato, ammette due strade alternative, il passaggio da A o da B. Basta allora che faccia la somma vettoriale finale sulle frecce. La QED e le sue regole ce lo impongono! L’evento invece che vuole un  passaggio registrato da A e un  “tic” in  R, ma che vuole anche un passaggio in B e un “tic” in R, non è un  singolo evento. Infatti, se abbiamo un passaggio da A non esiste strada alternativa: passare da A è l’unica strada possibile. Se, contemporaneamente, vogliamo che l’evento ammetta la possibilità del passaggio da B dobbiamo concludere che è una cosa del tutto diversa, dato che l’unica strada possibile è passare da B. L’evento non è uno solo, ma è composto da due eventi del tutto diversi.

Trattiamoli allora come tali. E’ facilissimo. (1) ci dice che se la luce può passare solo da A e arrivare in R, la probabilità finale è dell’1%, tale e quale al caso di un unico foro aperto. (2) ci dice la stessa identica cosa: la luce deve passare da B e arrivare in R. Nuovamente uguale al caso di un unico foro aperto. Anche la sua probabilità finale e l’1%. I due percorsi non sono vie alternative di un solo evento, ma sono due eventi complementari: o se ne segue uno o se ne segue un altro, tale e quale al caso della lastra con doppia riflessione e i due rivelatori messi in R1 (che raccoglie la luce riflessa) e in R2 (che riceve la luce trasmessa attraverso il vetro). Cosa dovevamo fare in quel caso: sommare tra di loro le probabilità dei due eventi, dato che la luce o fa una cosa o fa l’altra. Lo stesso capita adesso: anche se il rivelatore è adesso sempre lo stesso R, devo comunque sommare le percentuali dei due eventi differenti, dato che o capita (1) o capita (2).

Ripeto ancora, non fatevi ingannare dal fatto che il rivelatore rimanga sempre R. In parole povere, R fa un doppio lavoro: registra la probabilità dell’evento (1) e quello dell’evento (2), proprio come se avessimo fatto coincidere R₁ e R₂ nel caso della doppia riflessione. Non confondiamo nemmeno la situazione con quella delle Fig. 43 e 44. Nel caso attuale i due eventi non sono strade indipendenti che verificano lo stesso evento, ma due eventi completamente separati (li avevamo chiamati complementari), dato che in un caso è obbligatorio il passaggio da A e nell’altro il passaggio da B. Nel caso delle sorgenti X e Y, invece, volevamo verificare l’evento, definito così: partendo da X e da Y, due fotoni arrivano in A e in B . le strade XA e YB andavano moltiplicate perché erano vie indipendenti ma entrambe necessarie affinché l’evento si avverasse. Lo stesso capitava per YA e XB. Le due frecce ottenute da queste due azioni indipendenti, ma plausibili, si ricavavano attraverso la moltiplicazione e le loro ampiezze dovevano poi essere combinate con la regola della somma vettoriale, dato che erano vie alternative per l’attuazione dell’evento completo.

Pensiamo  anche a un problema aggiuntivo, ma facilmente risolvibile: “E se i fori non fossero tanto intelligenti? Ossia, se ogni tanto individuassero il passaggio e ogni tanto se lo “perdessero”?”. Ebbene, la soluzione è veramente ovvia: a mano a mano che scende la credibilità dei due fori  “intelligenti” l’interferenza aumenta e si avvicina al valore massimo che si ha con fori del tutto “ignoranti”! Insomma, si ha un mix delle due soluzioni, in quanto in certi casi vale l’evento unico e in altri l’evento spezzato in  due. E’ vero o non è vero che la QED è, in fondo, logicissima?

Questo articolo ci ha detto due cose molto importanti e fondamentali. Innanzitutto ci ha insegnato a stare molto attenti a definire un evento. Variazioni, che sembrerebbero non incidere, lo stravolgono completamente e lo spezzano addirittura in due eventi. Come conseguenza, abbiamo anche “capito” perché se i fori sono intelligenti il risultato è diverso. Non perché andiamo a curiosare quello che non dovremmo vedere, ma solo e soltanto perché abbiamo cambiato drasticamente l’evento, spezzandolo in due eventi del tutto separati. Potremmo anche  non voler sapere da che parte è passato il fotone, ma se esiste qualcosa (i rivelatori vicini ai fori) che potrebbe dirci da che parte è passato, vale, comunque, la separazione degli eventi. Si può anche dire che gli "stati" finali sono differenti, dato che adesso le condizioni finali sono, praticamente, distinguibili tra loro....

Attenzione! Questo ragionamento non risolve certo il problema di fondo della MQ e che tanto ha fatto e  fa ancora discutere gli esperti: chi e che cosa deve intromettersi sul percorso di un fotone perché lui diventi veramente una particella? Sembrerebbe che basti cambiare la struttura dell’evento e il gioco è fatto. Sì, ma come si cambia questa struttura? Se noi non potessimo verificare la diversità, la presenza del foro intelligente non servirebbe a niente. Quindi sembrerebbe che la nostra presenza ottica o uditiva (o quello che volete) sia sempre necessaria. E se ci fosse un gattino ad ascoltare il tic? O magari solo un’altra particella curiosa? O, molto più semplicemente, un qualcosa di esterno che si intromettesse in un fenomeno circoscritto e chiuso in se stesso?

Quest’ultima è la soluzione che preferisco… La particella si muove attraverso ampiezze di probabilità quando agisce in un sistema chiuso. Non appena viene a contatto con qualcosa che appartiene al mondo esterno (foro intelligente, occhio dell’uomo o anche quello del gatto) l’evento si modifica e l’onda collassa (tanto per usare il linguaggio più tipico della MQ). In parole più semplici, però, possiamo anche dire che se qualcosa dimostra che la particella fotone passa in un certo punto, tutti gli altri fotoni virtuali spariscono (e, in qualche modo, cadiamo nelle particelle entangled …).

Tuttavia, non possiamo seguire questa strada (adesso) e lascio a voi i confronti tra i vari modi di descrivere la MQ. Noi dobbiamo andare avanti con la QED che, adesso, utilizzando le poche regole definite finora (che sono perfettamente confermate dalla Natura), ci permette di descrivere  tutti i fenomeni della fisica, al di fuori della gravità e di ciò che capita dentro al nucleo atomico (ma in parte sì). Vi sembra poco? Direi proprio di no, dato che anche la chimica, la biologia e molto altro ancora si basano solo sulle interazioni tra luce e materia.  Accontentiamoci e vedrete che non saremo delusi!

Devo essere sincero fino in fondo. Le cose cominceranno a diventare un po’ più difficili e saremo obbligati a fare riferimento a qualche formula che non potremo, però, ricavare, dato che bisognerebbe entrare nella QED e nelle sue espressioni matematiche. Questo sarebbe troppo, anche per me… ve lo assicuro. Prenderemo per buone alcune conclusioni, ma capiremo cosa vogliono significare (questo è l’importante). Introdurremo anche il tempo, anzi lo spaziotempo e la trattazione ci porterà a concetti e a dimensioni difficilmente visibili con occhi normali. Abbiamo i mezzi per parlare e capire il linguaggio di Alice, ma l’impegno non sarà trascurabile.

Per inquadrare meglio il problema da un punto di vista generale (solo un momento, per non farci deviare dal discorso che stiamo mandando avanti) dobbiamo ricordare che due elettroni, ad esempio,  presi in due luoghi qualsiasi dell’Universo, indipendentemente dalla loro origine e dalla loro storia, hanno esattamente le stesse proprietà, vale a dire la stessa massa, la stessa carica elettrica e lo stesso spin (vedremo in seguito cosa sono esattamente). Questo fatto fondamentale si spiega attribuendo al campo da gioco, e non alle particelle, la realtà primaria.

I diversi elettroni sono ‘eccitazioni’ di una stessa realtà fondamentale, il campo elettrico, che pervade tutto l’Universo. Lo stesso vale per i fotoni, i quark, e le altre particelle. Forse queste poche e vaghe parole (che sono supportate da formule complicatissime) ci fanno capire meglio perché si fa sempre riferimento alla teoria dei campi. Sono loro le vere essenze dell’Universo e non tanto le particelle che sono soltanto una loro creazione più o meno momentanea. Questo ci spiega perché si è parlato di campo di Higgs piuttosto che di bosone di Higgs e perché si cercano le rotture di simmetria attraverso l’introduzione della teoria dei campi. Fermiamoci qui, dato che avremo abbastanza problemi da risolvere senza introdurci in “campi” troppo complessi per noi.

Tuttavia, queste considerazioni ci dimostrano un fatto fondamentale: le particelle di un certo tipo sono tutte uguali tra loro. Un fotone è identico a un altro fotone in tutto e per tutto. La cosa è ancora più vera se consideriamo luce monocromatica. Ebbene, PERCHE’ qualche fotone viene riflesso da una superficie di vetro e molti altri invece proseguono? Le condizioni sono uguali per tutti e non vi è nessuna ragione fisica perché si comportino in modo diverso. La “nostra” fisica classica ci ha abituato a spiegare la realtà delle cose attraverso un gioco continuo di causa ed effetto. Se qualcosa capita è perché è capitato prima qualcosa’altro: una catena di fenomeni che portano al verificarsi di un certo evento.

I fotoni, invece, sembrano proprio non accettare la fisica “normale”. E, come loro, tutte le particelle elementari. Esse sembrano scegliere in modo del tutto imprevedibile, ossia, seguono solo e soltanto la casualità. Un bel pasticcio per la nostra Scienza! Essa non può spiegare il perché di comportamenti slegati tra loro. L’unica possibilità è tralasciare il perché e limitarsi a descrivere le probabilità che ha un certo evento di compiersi in un certo modo. Si accettano i comportamenti assurdi delle particelle (anzi si fa finta di niente) e si calcolano solo e soltanto le probabilità che un certo evento ha di verificarsi. Non si spiega perché, ma si descrive come avvengono le scelte dei fotoni.

La meraviglia di tutto ciò è che lavorando in questo modo si ottengono risultati che sono perfettamente seguiti dalla Natura. Anzi, sembra proprio che la Natura usi questa strategia per creare i suoi fenomeni. Una Natura casuale, quindi? Beh… non sconfiniamo nel metafisico e proseguiamo con il nostro riassunto. Non facciamo girare Einstein nella tomba…

Fatta questa dovuta premessa, vediamo come abbiamo affrontato i fenomeni della Natura, attraverso il semplice (?) calcolo della probabilità che ha un evento di accadere sotto ben determinate condizioni di partenza, di arrivo e di svolgimento.

Ricapitolando

All’inizio abbiamo visto come un evento può essere descritto attraverso tutte le vie alternative che lo possono soddisfare. Queste vie alternative sono state rappresentate da frecce, che indicano l’ampiezza di probabilità che l’evento accada attraverso una certa strada. Abbiamo, poi, imparato come le frecce di ogni via alternativa possano essere sommate tra loro per determinare l’ampiezza di probabilità finale, il cui quadrato è la probabilità totale che l’evento accada.

In pratica, non sapendo spiegare, e quindi prevedere dove un certo fotone decide di andare, l’abbiamo trattato in termini di ampiezza di probabilità che ogni sua singola traiettoria ha di soddisfare l’evento. Ci siamo accorti che il fotone si comporta realmente nel modo descritto da questo approccio probabilistico, come dimostrato dalle caratteristiche che lo fanno manifestare un po’ come onda e un po’ come particella. In un certo senso, secondo una logica ancora legata al nostro pensiero comune: un fotone decide di seguire una certa strada solo dopo che l’ha percorsa. Solo il risultato finale dice al fotone di comportarsi in un certo modo oppure no, insomma una decisione presa dopo che la scelta è già stata fatta. Un vero assurdo, che cade, però, se introduciamo le ampiezze di probabilità capaci di collaborare e amplificare la probabilità finale oppure di annullarsi a vicenda.

Il fotone è rappresentabile come un insieme di ampiezze di probabilità che non hanno problemi ad aiutarsi a crescere o ad annullarsi, prima che il raggiungimento del traguardo le trasformino in particella. Avevamo descritto questo comportamento con la frase: il fotone è dappertutto e ha la stessa probabilità di essere dappertutto. In questo stato probabilistico, le singola probabilità di ogni possibile percorso si uniscono in maniera costruttiva e/o distruttiva:  l’unione fa la forza o la distrugge completamente.

L’evento va, però, definito perfettamente. Ad esempio: un fotone viene emesso da una sorgente A, deve passare da un certo punto B e, infine, raggiungere il rivelatore R è un evento diverso da: un fotone viene emesso da una sorgente A, deve passare da B o da C, e raggiungere il rivelatore R. Non tutte le traiettorie del fotone devono essere considerate, ma solo quelle che seguono le caratteristiche dell’evento. Bisogna stare bene attenti, quindi, a determinate tutte le vie alternative, ognuna con la sua freccia-ampiezza e alla fine sommarle con il metodo vettoriale. L’importante è che all’evento venga associata una e una sola ampiezza di probabilità finale. Le condizioni dell'evento determinano lo stato della particella.

Andando avanti, abbiamo, poi, analizzato un singolo evento e abbiamo cercato di dividerlo in passi successivi. Facendo questa analisi dettagliata abbiamo imparato come unire tra loro i vari passi, attraverso trasformazioni della freccia di probabilità. Trasformazioni che rispondono al nome di moltiplicazione. Operando in questo modo, siamo stati in grado di analizzare “pezzo a pezzo” le strade che soddisfano l’evento. Si sono prima moltiplicate le frecce dei vari passi in cui è stata scomposta una certa traiettoria, in modo da ottenete la freccia finale della traiettoria. Si sono poi sommate, come fatto precedentemente, le ampiezze di tutte queste frecce alternative per arrivare nuovamente all’ampiezza finale di probabilità dell’evento. Trovare il passo più piccolo in cui può essere scomposto un evento è fondamentale per la trattazione delle interazioni tra particelle.

Ricordiamo, ancora una volta, di essere ben sicuri di aver definito un certo evento. Se le ampiezze di probabilità finale si riferiscono a due eventi  separati, non si deve certo fare la somma vettoriale delle vie alternative, ma calcolare la probabilità finale dei due eventi (il quadrato dell’ampiezza) e poi sommarle “brutalmente” come si usa fare nella vita normale. In questo modo si ottiene la probabilità che accada o uno o l’altro degli eventi. Se i due eventi rappresentano tutte le possibili strade percorribili dal fotone, la probabilità finale deve essere uguale al 100%.

Abbiamo visto che l’operazione di moltiplicazione delle frecce si utilizza anche per traiettorie separate, più o meno contemporanee, che sono strettamente legate tra loro in quanto solo l’esecuzione di entrambe porta alla verifica dell’evento. Come possiamo stabilire se siamo in questo caso? Basta “leggere” bene l’evento. Se, ad esempio dice: parti da A e da B e arriva in C e D, risulta ovvio che la strada AC e la strada BD sono entrambe parti essenziali perché l’evento accada e quindi vanno moltiplicate tra loro, come se fossero passi successivi dello stesso evento. Analogamente lo sono i percorsi AD e BC (anch’essi soddisfano l’evento se effettuati entrambi) e anch’essi vanno moltiplicati tra loro. Le due coppie di percorso, così moltiplicate, portano ciascuna a un’ampiezza finale. Queste ultime vanno poi sommate, dato che rappresentano, ognuna, una via alternativa per l’intero evento.

Attenzione: finora abbiamo descritto eventi del tipo: parti da A , fai qualcosa o magari niente, e arriva in B. Come vedete non è stato assolutamente dato nessun vincolo temporale. L’importante è che si arrivi a destinazione. Il tempo importa soltanto per determinare la direzione della lancetta del celebre cronometro. Tuttavia, l’evento può compiersi in un attimo, così come in un tempo praticamente infinito. Il cronometro non impone niente, misura soltanto.

L' A, B e C di Alice

Il prossimo passo, invece, pone all’evento anche dei limiti temporali, del tipo:  parti da A al tempo t_A  e arriva in B al tempo t_B. L’evento diventa una vera e propria operazione che lega spazio e tempo, proprio l’azione che permette di studiare le interazioni tra fotoni ed elettroni. Bisogna, quindi, cambiare il campo da gioco ed entrare in quello del mondo di Alice, dove tutto può accadere, anche quello che avete sempre rifiutato perché apparentemente impossibile.

Perché ci sono servite tutte le operazioni precedenti, dato che ormai cambiamo campo da gioco? Beh… è stato fondamentale capire che le particelle, come il fotone, possono essere descritte perfettamente secondo ampiezze di probabilità. In tal modo sappiamo cosa significa associare a un certo percorso un’ampiezza, sappiamo come poterlo scomporre e che operazioni svolgere. La Natura vive nello spaziotempo e quindi i percorsi delle sue particelle devono essere definite in questo teatro.

La cosa più importante da fare è definire i passi più piccoli in cui un evento può essere scomposto. Essi diventano le lettere che permettono di scrivere le parole e le frasi necessarie a descrivere i fenomeni della Natura. Fortunatamente, questo alfabeto è molto semplice ed è composto da sole tre lettere, ossia tre azioni in grado di costruire tutte le parole e le frasi che descrivono le interazioni tra luce ed elettroni, una parte enorme della fisica della Natura. Noi ci occuperemo solo degli elettroni e dei fotoni, ma tutte le particelle partecipano a questo gioco così semplice e così complesso.

Quando consideriamo i fotoni su scale molto grandi (ben maggiori rispetto al tempo necessario alla lancetta del cronometro di fare un giro completo) i fenomeni che osserviamo sono approssimati molto bene dalla regola “comune”: la luce viaggia in linea retta, dato che vi è un numero sufficiente di traiettorie, intorno a quella del tempo minimo di percorrenza, tali da rinforzarsi una con l’altra, così come vi sono abbastanza traiettorie alternative che si cancellano tra di loro. Ma quando i percorsi che può compiere il fotone diventano troppo piccoli, abbiamo già scoperto che la regola generale perde di significato e nascono fenomeni di interferenza, ecc. Lo stesso capita per l’elettrone.

Quando è costretto a stare in spazi ristretti, come all’interno di un atomo, tutte le traiettorie sono possibili e bisogna trattarlo attraverso ampiezze di probabilità. Anche per loro nascono i fenomeni di interferenza e solo la somma delle frecce è in grado di descrivere dove la particella possa trovarsi con maggiore probabilità.

In generale, ogni particella naturale si comporta nello stesso modo (quark, gluoni, neutrini, ecc., ecc.).

I diagrammi di Feynman sono le frasi che possono essere scritte con il nuovo alfabeto. Essi permettono una rappresentazione grafica e simbolica di tutte le possibili relazioni fra particelle, come descritte dalle leggi della meccanica quantistica e della teoria dei campi. Essi diventano veri e propri strumenti di calcolo per le probabilità dei vari processi fisici. Hanno quindi una doppia faccia: (1) consentono di tradurre ogni diagramma nella formula corrispondente e viceversa, attraverso un alfabeto unico; (2) danno una descrizione visiva e intuitiva del processo che si sta studiando, permettendo di fare considerazioni fisiche su di esso prima ancora di aver calcolato le espressioni matematiche corrispondenti.

Cerchiamo di esprimerci con altre parole, forse più semplici.

I diagrammi di Feynman riescono a rendere visibile qualcosa che non lo potrebbe essere assolutamente. La QED è, in realtà, una storia puramente matematica, in cui la Natura è trattata secondo leggi probabilistiche che riescono, però, a descriverla in modo perfetto. Ne abbiamo avuto un assaggio fino ad adesso, limitandoci alla luce. Una freccia e un cronometro (vedremo che il cronometro diventerà qualcosa di ben diverso, tra non molto) ci hanno permesso di verificare e descrivere tutti i fenomeni legati all’ottica. Tuttavia, siamo ancora con un piede nel mondo reale e un piede nel mondo di Alice. Parliamo il linguaggio della regina e del cappellaio matto, ma lo utilizziamo per disegnare situazioni ed eventi associati alla vita di tutti giorni: uno specchio che riflette la luce, una superficie che la trasmette, una lente che la focalizza, due fenditure che l’amplificano e/o l’annullano, ecc., ecc. Disegni “normali” tracciati in uno spazio “normale”, descritti attraverso quantità “anormali”, di tipo puramente probabilistico.

Un evento si verifica in un certo modo solo perché quel modo ha la massima probabilità di accadere. Si possono anche eliminare tutte le vie alternative per l’ottenimento dell’evento, dato che la loro probabilità è, per lo più, del tutto trascurabile. Questa semplificazione può essere descritta perfettamente  giocando con una freccia di probabilità che si accorcia e ruota a seconda del modo scelto per attuare l’evento. Traiettorie assurde non vengono escluse a priori, ma a posteriori, quando è stata verificata la loro inutilità o rarità. Tuttavia, le rappresentazioni finali, anche se basate su regole a prima vista senza alcun riscontro nella fisica comune, permettono di tracciare diagrammi e descrivere eventi che fanno parte della nostra vita. Dire: la luce parte da S e arriva R, riflettendosi su uno specchio è un evento comune, il cui risultato coincide con quanto siamo abituati a vedere. Cambiano solo le regole applicate per arrivarci.

Di tanto in tanto ci siamo, però, scontrati anche con episodi inaspettati, come quelli che ci hanno dimostrato che la luce, sotto certe condizioni, può anche seguire traiettorie non rettilinee, ma parimenti probabili. Per non parlare del fotone che sembra poter passare contemporaneamente da due fori e creare l’interferenza, ma -se “guardato”-  sembra comportarsi normalmente, da particella concreta, e dar luogo a una “raffica” di colpi associati a veri “proiettili”. Le regole della QED ci hanno permesso di “capire”, a modo loro, che non vi è alcuna contraddizione.

Questo sistema un po’ astratto e un po’ concreto ci ha quasi permesso di fare amicizia con l’ampiezza di probabilità, un qualcosa che pur essendo puramente matematico può vivere e comunicare nella realtà di tutti i giorni.

Adesso, ciò non è più possibile. Per vivere nel mondo di Alice, e muoversi e parlare come i suoi personaggi, bisogna costruire un campo di gioco astratto e non percorribile se non con la matematica. Sembrerebbe impossibile tentare qualsiasi rappresentazione grafica. Tuttavia, Feynman ha fatto nascere i suoi diagrammi, un capolavoro astratto e concreto che permette agli abitanti del Paese delle Meraviglie di esprimere i propri concetti assurdi attraverso semplici linee e traiettorie.

Attenzione, però: guai a cercare di vederli come rappresentazioni paragonabili a quelle del mondo normale. Esse sono frasi matematiche pure e semplici a cui è stata data una veste fittizia. Normalmente, la Scienza, quando giunge a certi punti, chiude la porta della semplificazione e si cala in formule sempre più complesse e astruse. Feynman no. Crea un capolavoro descrittivo. Non solo associa a certe operazioni matematiche una rappresentazione grafica di estrema semplicità visiva, ma permette di svolgere ogni operazione successiva, ogni trasformazione che porti a nuove descrizioni matematiche, solo attraverso le modifiche grafiche dei suoi diagrammi.

Qualsiasi cosa si esegui graficamente nei diagrammi, e segua poche e ben definite regole, porta a un risultato che può essere immediatamente tradotto nella sua formulazione matematica più accurata e perfetta. Chi disegna nel mondo di Alice-Feynman sa che qualsiasi variazione esegua nei grafici non è altro che una trasformazione matematica di estrema accuratezza. Quando l’opera è completata, diventa, quindi, immediato, per gli abitanti del mondo di Alice, passare alla formulazione matematica corrispondente.

E’ come se si usasse una scorciatoia che simbolicamente descriva trattazioni di una complessità inaudita, basate solo su concetti astratti. La scorciatoia, che chiunque potrebbe eseguire e descrivere con facilità relativa, equivale, perciò, a un insieme di passaggi matematici, di interazioni e trasformazioni, incomprensibili alla persona normale, che possono, però, essere descritti visivamente da chiunque.

In conclusione, solo pochi studiosi della meccanica quantistica possono seguire i passaggi reali, basati su pura matematica (noi no di certo), ma attraverso i diagrammi e seguendo poche regole si ottengono i risultati voluti, lasciando da parte tutti i passaggi matematici. Il diagramma finale descrive ciò che solo la matematica avrebbe potuto trovare, ma lo fa con un linguaggio comprensibile a tutti. La trasformazione del risultato in un’espressione matematica è poi facile solo per gli addetti ai lavori, ma a noi resta chiaro il concetto che vuole descrivere.

Scusate se continuo a ripetere lo stesso concetto in vari modi alternativi (senza dover sommare le ampiezze, però…), ma è troppo importante capire cosa ci troveremo di fronte e come dovrà essere  trattato. Ancora più semplicemente: non vi è bisogno di eseguire tutti i passaggi matematici reali, ma solo e soltanto tracciare poche linee nel mondo illusorio di Feynam e poi, alla fine, tornare nel mondo matematico sapendo che il risultato è sicuramente perfetto.

Tuttavia, e dobbiamo sempre ricordarcelo, i diagrammi sembrano percorsi, movimenti, incontri del tutto “normali”, ma non lo sono assolutamente e niente hanno a che fare con la nostra visione del mondo. Alice deve dimenticare tutto ciò che ha imparato a scuola e iniziare a disegnare in un mondo nuovo e con un alfabeto nuovo. Nei digrammi di Feynman si può invertire la freccia del tempo, si può creare una particella e ingoiarla, si può passare dalla materia all’antimateria e mille altre cose, solo con pochi tratti di matita. Ma guai a convincerci di stare rappresentando qualcosa che possiamo toccare con mano.

In altre parole, i diagrammi permettono di rappresentare processi matematici mostruosamente difficili con pochi segni su un foglio e, d’altra parte, qualsiasi cambiamento dei segni sul foglio corrisponde perfettamente a equazioni matematiche plausibili e dimostrabili. Le linee sono talmente adatte al mondo di Alice che anche manovrandole “a caso” si ottiene, comunque, qualcosa che ha un senso matematico perfetto. Rimangono, però, sempre e comunque linee e percorsi preclusi alla nostra vita normale.

Spero di essere stato compreso e di aver dato un’idea della grandezza del genio matematico di Feynman: non solo è stato in grado di scrivere la matematica che porta a certi risultati pratici, ma l’ha resa descrivibile graficamente talmente bene che basta operare sui disegni per ottenere gli stessi risultati di operazioni intricate e complicatissime. Sapendo che la linea (1) rappresenta una certo concetto e la linea (2) un altro e conoscendo solo tre regole di comportamento, qualsiasi elaborazione venga fatta sul foglio (che segua le regole, ben inteso) porta a una qualcosa di completamente nuovo che, però, può essere perfettamente traducibile in termini matematici.

E’ come se partissi con due oggetti reali ed entrassi nel mondo di Alice. I due oggetti cambierebbero forma, dimensioni, essenza stessa. Io li potrei manipolare, combinare secondo le loro nuove e incomprensibili caratteristiche fino a ottenere un oggetto assurdo e del tutto nuovo. Ritornando nel mondo normale l’oggetto acquisterebbe immediatamente una forma e una dimensione conosciuta.

Un abbraccio indissolubile

Forse ho parlato fin troppo ed ho ripetuto lo stesso concetto fino alla nausea. Il succo è che per potere manipolare i diagrammi di Feynman è necessario entrare nel mondo di Alice e questo mondo non è altro che lo spaziotempo, un sistema di assi cartesiani che possiamo facilmente semplificare in due sole coordinate: lo spazio (asse x) e il tempo (asse y). Ognuno dei due assi ha un verso ben definito, ovviamente. Tuttavia, qualsiasi percorso si faccia su di esso non ha niente a che vedere con la nostra realtà quotidiana. Noi spostiamo le cose nello spazio e il tempo passa in modo indipendente. Per andare da A a B devo cambiare le coordinate del punto A e farle diventare quelle del punto B. Posso usare qualsiasi mezzo, ma ho descritto solo e soltanto un movimento nello spazio. Mentre faccio questa operazione, però, il tempo passa, e non ha veramente influito sulla traiettoria spaziale. Nello spazio-tempo non esistono percorsi reali, ma solo traiettorie simboliche perfettamente descrivibili matematicamente. L’importante è NON CONFONDERLE MAI.

Il problema è lo stesso di quando disegniamo l’Universo che si espande nel tempo attraverso un palloncino o -più semplicemente- attraverso un  cerchio che si allarga sempre più. Quante volte l’abbiamo usato? Eppure, ogni tanto qualcuno si sbaglia e pretenderebbe di far muovere un oggetto secondo una linea spaziotemporale. No, questo non  è possibile. Gli spostamenti spaziali avvengono solo lungo il  cerchio. Il raggio è dominio del tempo e non si può attraversare. Quante volte è stata ripetuta questa frase? E quante volte è stato disegnato il cono di luce? Esso è il tipico esempio di una linea immaginaria, esistente solo nello spazio-tempo, nel mondo di Alice. Solo lì si può disegnare senza commettere errori madornali. Tuttavia, ciò vuole anche dire che non possiamo disegnare nello spazio-tempo una percorso realistico, ma solo simbolico. Non c’è altro da fare, la porta con il vecchio mondo si è chiusa dietro ad Alice. Solo con questa idea in testa, solo non cercando di vedere nei diagrammi di Feynman il vero movimento di un fotone o di un elettrone si potrà elaborarli e usarli con destrezza. Altrimenti, ne saremmo subito esclusi.

Anche se non saremo mai in grado di esprimere il significato matematico e completo di queste azioni, saremo però in grado di comunicare e descrivere concetti come materia, antimateria, creazione e distruzione, trasformazione di particelle in altri tipi di particelle, leggi di conservazione, simmetrie, ecc. ecc. E, non ultime, proprio le caratteristiche intrinseche della materia e quindi il perché la luce si riflette o si rifrange quando incontra un pezzo di vetro… (ma non perché un fotone fa una certa azione e un altro ne fa un’altra… questo resta un mistero).

Concludo questa parte del tutto vaga e preparatoria con un esempio che verrà molto utile quando inizieremo il nostro percorso nel microcosmo delle particelle. Anche se non possiamo ancora capire cosa significhino certe frasi, il concetto generale può servire per entrare nel nuovo campo da gioco.

Un gioco di squadra

Consideriamo due giocatori di pallone: il primo ha la palla e la passa al compagno che va a rete. Quando il primo lancia la palla, trasmette la sua energia o forza o -molto meglio- la sua quantità di moto al compagno. Effettuato il lancio, cambia traiettoria, tornando, ad esempio, verso il centrocampo o versi i bordi del rettangolo di gioco; allo stesso modo, quello che riceve la palla modifica a sua volta la propria direzione e va verso la rete. La medesima cosa succede tra due elettroni. Quando si avvicinano tra loro, il primo cede al secondo un fotone, detto "virtuale", perché impossibile da rivelare. Entrambi gli elettroni modificano la propria traiettoria, cambiando direzione come se si fossero respinti senza toccarsi.

Questo è uno dei classici esempi dei diagrammi di Feynman. Rappresentabile facilmente con poche linee, ma guai a volerlo vedere come una rappresentazione concreta. Essa è rappresentazione simbolica che avviene in un mondo estraneo a quello comune. Non vi sarà scappato, però, che questo semplice diagramma introduce le particelle mediatrici delle forze. Il pallone, in realtà, è virtuale, ma collega le azioni dei due elettroni. Non solo, ma permette a due particelle con la stessa carica di respingersi. Poche linee e … concetti fondamentali della fisica compaiono in tutta la loro concretezza.

Non so se tutte queste parole siano servite veramente a qualcosa. Forse hanno solo confuso le idee. Poco male, potete anche dimenticarvele, dato che tra poco entreremo effettivamente e con la massima semplicità descrittiva nel mondo di Alice, ossia nello spaziotempo. Cominceremo da zero, ma con la mente preparata a non confondere la realtà quotidiana con quanto verrà descritto.

Iniziamo il nostro viaggio verso i diagrammi di Feynman: forza, coraggio e molta attenzione.

Tre lettere per scrivere la Natura

La prima cosa da chiedersi è: “Dopo aver convissuto a lungo con le ampiezze di probabilità e avere imparato a sommarle, a moltiplicarle e a spezzarle in parti sempre più piccole, possiamo definire in qualche modo i sub-eventi “elementari”? In altre parole, è possibile selezionare pochi “pezzi” fondamentali, come fossero lettere di un alfabeto, che ci permettano di descrivere attraverso parole e frasi ogni fenomeno della Natura? E se fosse vero, quante sarebbero queste lettere?”. Beh… siamo veramente fortunati. La risposta è positiva e il numero è ridicolo: solo tre azioni sono sufficienti a descrivere ogni possibile fenomeno associato alla luce e agli elettroni, ossia alla luce e alla materia.

Prima di enunciarle, ricordiamo, ancora una volta, che sia per i fotoni che per gli elettroni vale una regola generale: se entrambi vengono considerati su scale molto grandi, si dimostrano a tutti gli effetti come particelle, ma il loro comportamento cambia drasticamente se li si analizzano su scale molto piccole. Pensate ad esempio agli elettroni. All’interno di un atomo, essi perdono del tutto le loro caratteristiche di corpuscoli, dato che non vi è posto per traiettorie  e orbite ben definite. Essi, come i fotoni, possono solo essere descritti come ampiezze di probabilità di occupare una certa posizione. Anche per loro si devono sommare frecce e le interferenze diventano di primaria importanza.

Vedremo che non solo gli elettroni si comportano così, ma tutte le particelle elementari, come gluoni, quark, neutrini e compagnia bella.  Un discorso ben più generale di quanto non ci racconti l’interazione tra luce ed elettroni. Tuttavia, proprio per le caratteristiche simili, possiamo benissimo limitarci, per adesso, a fotoni ed elettroni.

Definiamo, finalmente, le tre azioni (tre e solo tre) che stabiliscono l’alfabeto per tutte le frasi della QED, ossia per tutti i fenomeni che ci mostra la Natura.

(1) Un fotone viaggia da un punto a un altro.

(2) Un elettrone viaggia da un punto a un  altro.

(3) Un elettrone è capace di assorbire o di emettere un fotone.

Siete delusi? Probabilmente sì, dato che a parte la (3) sembra di avere detto cose di un’ovvietà mostruosa. La (3) appare un po’ più impegnativa e va sicuramente studiata in dettaglio. Tuttavia, anche le altre due sono decisive e importanti, dato che devono essere descritte nel nuovo campo di gioco di Alice, ossia lo spaziotempo.

Ricordiamo, inoltre, che ognuna di queste azioni ha una sua ampiezza di probabilità (una freccia) che può essere calcolata secondo regole ben definite. Queste regole sono ferree e non bisogna dimenticarle, anche se una loro rappresentazione completa abbisogna di una matematica superiore. Nessun problema, dato che noi le tratteremo solo graficamente. Per fare ciò, però, è necessario preparare il foglio del disegno e questo è un qualcosa che ha bisogno di essere compreso perfettamente nella sua essenza, senza fare confusione con lo “spazio” in cui viviamo.

Non è la prima volta che disegniamo lo spaziotempo, ma ogni volta si rischia di fare un po’ di confusione. Ricominciamo, quindi, da zero e consideriamoci dei bambini che si avvicinano a un quaderno per la prima volta e cercano di scrivere sulla sua prima pagina le uniche tre lettere dell’alfabeto.

Un quaderno molto speciale

La pagina del quaderno non ha righe o quadretti. E’ completamente bianco. Sta a noi preparala per ciò che vogliamo rappresentarci sopra. Permettetemi qualche esempio: se volessimo disegnare il profilo dell’Italia, dovrei mettere come coordinate delle distanze o -se preferite-  la latitudine e la longitudine. Se, invece, volessimo vedere com’è variata la popolazione della Terra, dovremmo inserire il numero di abitanti e gli anni. Se, ancora, volessimo sapere la struttura della nostra atmosfera, metteremmo come coordinate, ad esempio, la temperatura e l’altezza dal suolo. E mille altri esempi simili. Ogni disegno, magari proprio lo stesso (una retta, un quadrato, un cerchio o quello che volete), acquista un significato diverso se si cambiano gli assi di riferimento.

Nella pagina di Alice, pronta per ricevere le tre lettere della QED, si devono inserire lo spazio e il tempo. Un bel pasticcio, dato che lo spazio è definito da tre dimensioni. Se gli aggiungiamo il tempo, avremmo bisogno di quattro dimensioni. Come potremmo mai trasformare un foglio in un campo di gioco a quattro dimensioni? Impossibile anche per la QED e le sue lettere.

Poco male, dato che conosciamo già la semplificazione che si può fare senza ledere i concetti base: basta considerare lo spazio come una retta, ossia assumere che ogni punto dello spazio e ogni traiettoria percorribile sia contenuta nell’asse delle x. Lo abbiamo fatto spesso e, in fondo, non ci ha mai spaventato più di tanto. Possiamo accettare questa semplificazione, mettendoci, però, bene in testa che qualsiasi movimento spaziale di una particella può avvenire solo lungo la linea orizzontale. I fenomeni di riflessione, rifrazione e cose del genere, che abbiamo trattato precedentemente, avvengono, perciò lungo questa retta.

No, non sto dicendo cose assurde o banali. Tra poco, vedremo che le particelle sembreranno riflettersi o rifrangersi, ma non commettiamo l’errore di pensare  a qualcosa che si muova diagonalmente nello spazio, come succedeva alla luce che si dirigeva verso uno specchio o usciva da una fenditura. Mi raccomando!

A questo punto, l’asse y è libero e può essere regalato al tempo. Il nostro foglio è diventato lo spazio-tempo. Per prendere dimestichezza con questo campo da gioco, impariamo, innanzitutto, a disegnarci sopra qualcosa che si riferisca alle azioni di tutti i giorni. Visto che l’abbiamo considerato un campo sportivo, consideriamo come “oggetto” da rappresentare una pallina da tennis, come vediamo nella Fig. 47.

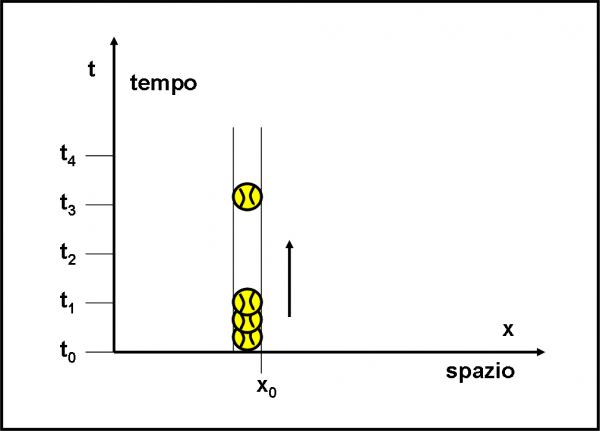
Immaginiamo che la pallina sia ferma, in un certo punto del “normale” campo da tennis (che è tutto contenuto nell’asse x). Il tempo, invece, continua a scorrere andando verso l’alto (attenzione: la freccia del tempo ha questo verso e sarà sempre lo stesso). Come possiamo disegnare la nostra pallina in questo campo da gioco veramente speciale? Non certo come un punto, dato che la sua coordinata “tempo” continua a cambiare. Non cambia invece la x₀, ossia la sua posizione nello spazio. Il movimento spazio-temporale della pallina è quindi una linea verticale. In questo campo da gioco, la pallina ha una ben definita traiettoria, alla quale possiamo associare un’ampiezza di probabilità di accadere.

Aggiungiamo, adesso, alla figura precedente una parete  che al tempo t₀ si trova in x₃ (Fig. 48).

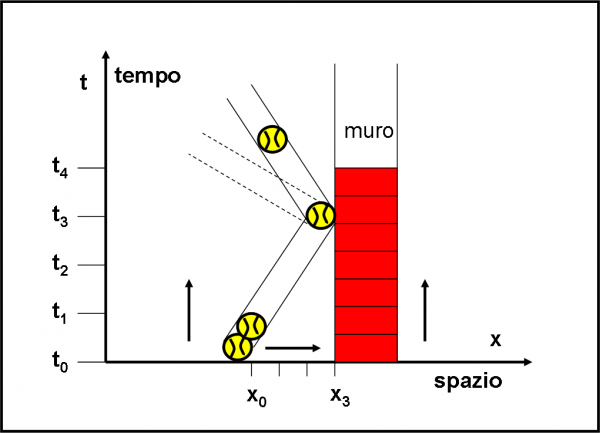
Essa non può certo cambiare posizione spaziale e quindi al passare del tempo mantiene sempre la stessa posizione e descrive la traiettoria parallela all’asse del tempo (come faceva la pallina nel caso precedente). Adesso, però, la pallina si muove in modo uniforme nello spazio andando verso la parete. Al tempo t₀ si trova in x₀, al tempo t₁ in x₁ e via dicendo, fino a toccare la parete al tempo x₃. Non riuscendo, ovviamente, a penetrare dentro la parete, la pallina è costretta a rimbalzare e al tempo t₄ si trova nuovamente nella posizione x₂ e in t₅ in x1. Non è detto, però, che la pallina torni indietro nello spazio così come si è mossa all’andata. Potrebbe, ad esempio tornare in x₀ al tempo t₄ (ossia, muoversi più velocemente che all’andata, avendo percorso uno spazio maggiore in un tempo uguale), oppure in x₁ al tempo t₄ (si muoverebbe più lentamente). La pallina, in ogni caso, descrive una traiettoria spazio temporale che a un certo momento (impatto con la parete) cambia percorso, tornando da dove era venuta. La pallina si è sicuramente mossa anche nello spazio, ma ha percorso il tratto da x₀ a x₃ e poi è tornata indietro lungo la stessa direzione. In qualche modo, dal punto di vista spaziale, la pallina ha invertito di 180° la sua direzione di marcia.

Nel foglio spazio temporale ha invece descritto una linea spezzata. Essa rappresenta una traiettoria spazio temporale che possiede una certa ampiezza di probabilità di essere realmente percorsa. Attenzione: so di essere noioso, ma vi prego di non confondere la figura precedente con la visione puramente spaziale, in due dimensioni, dell’urto di una pallina tirata contro un muro diagonalmente. Se pensiamo a questo, fermiamoci, scrolliamo la testa e rimettiamo sullo zero il nostro cervello!

Beh… penso proprio che non abbiate difficoltà a ricordare cosa significhi la traiettoria nel piano spaziotempo: il suo coefficiente angolare è la velocità della pallina, ossia lo spazio percorso in un certo intervallo di tempo. Più la retta è inclinata rispetto all’asse delle x e minore è la velocità relativa.

Dato che a noi non interessano le palline da tennis (troppo grandi, così come le dimensioni di un vero campo da tennis), ma le particelle come i fotoni e gli elettroni, cerchiamo di trasformare la scala degli assi cartesiani x e t.

Il fotone, su spazi abbastanza lunghi e nel vuoto, viaggia lungo una linea retta (lo abbiamo dimostrato). La sua velocità può essere considerata costante e si indica con c, che vale circa 300 000 km/sec. Mettere i metri in ascissa e i secondi in ordinata sarebbe una pessima scelta della scala, dato che tutte le particelle viaggiano molto velocemente. Scegliamo, allora, la scala in modo che la traiettoria di un fotone che viaggia a velocità c sia descritta da una retta a 45°. Ciò vuol dire che un intervallo pari a n centimetri o millimetri o metri o quello che preferite deve essere “lungo” come l’intervallo di tempo che la luce impiega a percorrere n. Se n fosse di 30 centimetri, lo stesso segmento sull’asse y sarebbe pari a un miliardesimo di secondo, così come un intervallo di 300 000 km corrisponderebbe esattamente a un secondo.

Con questo cambiamento di scala, la velocità di un fotone che descriva la traiettoria spazio-temporale da x₁,t₁ a x₂,t₂ (o da x2,t1 a x1,t2) è proprio c (Fig.49).

La cosa veramente importante è però, un’altra: se la traiettoria è più ripida della retta a 45° la velocità è minore di c (minore spazio nell’unità di tempo), mentre se la retta è meno inclinata di 45°, la velocità è maggiore di c (maggiore spazio nell’unità di tempo). Notate che abbiamo scelto (anzi, l’ha deciso Feynman) una rappresentazione simbolica per il fotone: lo abbiamo descritto come una linea ondulata. Niente a che vedere con un’onda, dato che tutte le particelle si comportano nello stesso modo. E’ solo una scelta per riconoscere i fotoni dai suoi amici di avventura.

Fermiamoci un attimo per vedere come ciò che abbiamo introdotto si potrebbe applicare alla vita di tutti i giorni. Infatti, anche noi possiamo tracciare le traiettorie di un certo oggetto nello spazio-tempo. Tuttavia, abbiamo dei blocchi fisici insormontabili. Consideriamo la Fig. 50, dove l’oggetto P può muoversi verso il futuro alla sua massima velocità, ossia c (ce l’ho dice il Sig. Einstein e lui di macrocosmo se ne intende e molto!).

Otteniamo una coppia di rette che formano un angolo di 90° tra di loro. Esse possono, infatti, essere inclinate di 45° rispetto all’asse dello spazio, non uno di meno, altrimenti accetteremmo velocità maggiori di quelle della luce. Qualsiasi traiettoria contenuta all’interno delle due rette è possibile, mentre quelle esterne sono IMPOSSIBILI per definizione. Vi è però un altro vincolo. L’oggetto non può descrivere traiettorie che vadano in verso opposto, dato che vorrebbe dire viaggiare verso il passato. Anche questo caso è vietato dalla fisica. Le uniche traiettorie possibili sono quindi quelle contenute nella parte bianca del diagramma. Esso è un triangolo che altri non è che la sezione, nel piano della figura, del cono di luce futuro di un oggetto P.  Il nostro modo di vivere ha a disposizione solo una piccola parte del foglio! Nel mondo di Alice, invece, qualsiasi traiettoria è possibile.

Torniamo al nostro fotone. Lui è libero di muoversi dove vuole. Ricordo ancora che il foglio rappresenta una parte di spaziotempo piccolissimo, dove è possibile qualsiasi cosa, come, ad esempio (e lo abbiamo già visto) andare lungo traiettorie che non sono rettilinee (esperimento della doppia fenditura) e che possono causare fenomeni “assurdi” come l’interferenza. E’ il momento di introdurre la prima lettera del nostro alfabeto.

Abbecedario

Essa dice: un fotone viaggia da un punto a un altro. In parole più tecniche questa lettera significa: un fotone che occupa una posizione (x₁,t₁) ha una certa ampiezza di probabilità di apparire in (x₂,t₂). Questa ampiezza di probabilità viene indicata con P(A -->B) o, più facilmente, P(A,B). Il calcolo di P(A,B) non è cosa banale, ma la matematica è capace di farlo con grande accuratezza. L’ampiezza dipende essenzialmente dalla differenza x₂-x₁ e dalla differenza t₂–t₁. Più esattamente dalla differenza dei loro quadrati, ossia (x₂-x₁)² – (t₂-t₁)². Risulta immediato accorgersi che la traiettoria rettilinea tra A e B è proprio quella per cui questa differenza diventa zero, ossia quando x₂-x₁ = t₂-t₁, cioè quando la traiettoria rappresenta la velocità della luce convenzionale, uguale a c.

Possiamo facilmente concludere che l’ampiezza totale P(A,B) è la somma di tante ampiezze e che quelle intorno alla velocità della luce c danno il maggior contributo all’ampiezza di probabilità finale. Lo stesso identico discorso che avevamo fatto quando avevamo dimostrato perché la luce, su grandi distanze, si muove di moto rettilineo. Abbiamo cambiato campo di gioco, ma le regole sono sempre le stesse, quella della QED.

Ricapitoliamo un attimo: nei capitoli precedenti avevamo visto che la luce può anche non andare lungo traiettorie rettilinee. Adesso, nel mondo di Alice e sul suo quaderno, abbiamo visto che la luce può anche viaggiare a velocità diverse da c. Un bell’inizio, non c’è che dire! Il contributo di traiettorie diverse da quelle del senso comune possono non essere trascurabili quando gli spazi da percorrere sono estremamente piccoli. L’interferenza ce lo ha dimostrato e possiamo aspettarcelo anche adesso.

Nel piano spazio-temporale l’azione di andare da A a B viene indicata, come già detto, da una linea ondulata che congiunge A con B. A questa linea è associata la corrispondente P(A,B). P(A,B) è data da una formula che ci è preclusa, ma sappiamo molto bene come si trattano le ampiezze di probabilità! Forse non ce ne siamo accorti, ma la prima lettera del nuovo alfabeto (un fotone va da un punto a un altro) è in grado di descrivere tutta l’ottica e i fenomeni ad essa collegati. Essa rappresenta l’intera teoria della luce.

Nota Bene: in realtà, quanto detto non è proprio vero, dato che, finora, abbiamo trascurato la polarizzazione della luce. Se avremo voglia potremo anche introdurla, ma le cose si complicherebbero un bel po’, non cambiando, però, il succo dell’intera faccenda.

Passiamo alla seconda lettera dell’alfabeto, ossia alla seconda azione fondamentale: un elettrone va da un punto a un altro (ovviamente, sempre nello spaziotempo). Sembra un’ovvietà, un’estrapolazione immediata della prima lettera. In realtà, la formulazione dell’ampiezza di probabilità associata all’elettrone è più complicata di quella del fotone. Anch’essa dipende dalle differenze tra spazio e tempo, come quella del fotone. Tuttavia, vi sono vari termini aggiuntivi che vengono moltiplicati per un certo numero m. In parole poverissime, l’ampiezza di probabilità E(A,B) dell’elettrone è una combinazione praticamente infinita di P, ognuna moltiplicata per m². Ciò deriva dal fatto che un elettrone per andare da A a B può eseguire diversi cambiamenti di rotta. Può andare, ad esempio, fino a C e poi piegare per finire in B. Un cambiamento di direzione comporta l’aggiunta, al termine “base” P(A,B), di un termine dato da P(A,C) x m² x P(C,B). L’elettrone potrebbe, però, fare due cambiamenti di direzione: andare da A a D, poi da D a E, e, infine, da E a B. L’ulteriore termine da aggiungere sarebbe P(A,C) x m² x P(C,D) x m² x P(D,B). e via dicendo fino all’infinito o quasi. In poche parole m² non è altro che l’ampiezza relativa a un cambiamento di direzione. Ovviamente, più passaggi intermedi si considerano  e maggiore è il contributo di questi all’ampiezza di probabilità E(A,B).

Non vi sarà scappato il fatto che abbiamo eseguito una moltiplicazione di ampiezze, dato che l’ampiezza finale è stata scomposta nei suoi vari passi. Non andiamo oltre perché entreremmo nella matematica più complessa a noi preclusa. Tuttavia, possiamo concludere che l’ampiezza di probabilità del percorso dell’elettrone per andare da A a B è data da E(A,B) e che essa coincide con quella del fotone, quando il numero m diventa zero (tutti i termini aggiuntivi si eliminano).

Torneremo su m, ma, per adesso, accettiamo che l’ampiezza di probabilità di andare da A a B, da parte dell’elettrone, è data da E(A,B), che è quantità piuttosto complicata, ma strettamente collegata a P(A,B). L’azione dell’elettrone viene indicata nel diagramma da una linea continua che congiunge A con B, ma sappiamo benissimo che essa rappresenta un’infinità di linee spezzate, ciascuna con la sua ampiezza, che contribuiscono al valore finale di E(A,B).

Non ci rimane, adesso, che introdurre la terza lettera, quella apparentemente meno immediata: un elettrone è capace di assorbire o di emettere un fotone. Innanzitutto, facciamo una chiara affermazione: non vi è nessuna differenza sostanziale tra le due azioni sopra descritte. Assorbire o emettere un fotone non cambia assolutamente il processo. Questa azione viene chiamata “accoppiamento” (coupling in inglese). La traiettoria dell’elettrone viene simbolicamente cambiata al momento di un accoppiamento. L’ampiezza di probabilità dell’accoppiamento non ha una formula particolarmente difficile. Essa si riduce a un numero j, che comporta una riduzione di circa 0.1 e una rotazione di 180°.

Come possiamo rappresentare nel nostro foglio questa terza azione? Facilissimo: due linee continue (l’elettrone) (munite di una freccia che indica il verso di percorrenza, cosa inutile per il fotone dato che per lui essere emesso o assorbito è la stessa cosa) e una un linea ondulata (il fotone), come rappresentato in Fig. 51. Ogni linea ha una sua ampiezza di probabilità, così come l’accoppiamento.Tuttavia, assumendo che il fotone si muova nel verso crescente del tempo (per adesso è meglio rimanere con i piedi per terra), possiamo dire che nella figura il fotone è assorbito. Ci torneremo, comunque, sopra.

Non è assolutamente difficile lavorare su di esse per descrivere situazioni più elaborate.

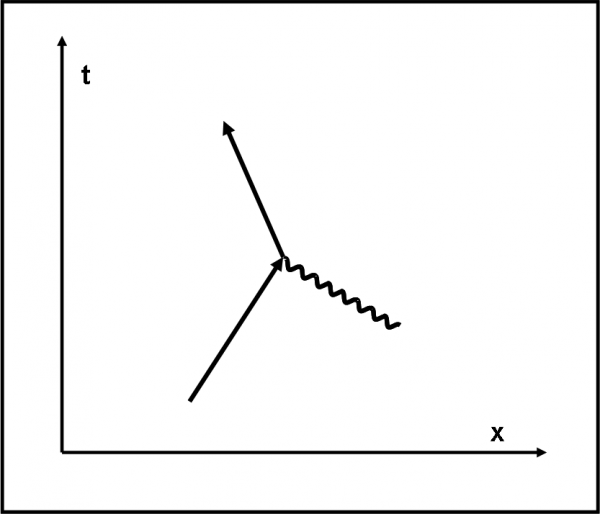
Iniziamo, dunque, questa impresa. Abbiamo imparato le lettere dell’alfabeto, le abbiamo definite esaurientemente e sappiamo come disegnarle. Proviamo adesso a costruire con esse la prima parola!

Gli elettroni devono tenersi a distanza

Ne scegliamo una semplicissima, che mostri tutte e tre le lettere fondamentali. Descriviamo accuratamente l’evento che vogliamo rappresentare e poi disegniamolo attraverso le lettere appena imparate. Vogliamo calcolare la probabilità che due elettroni, posti in 1 e 2, finiscano nei punti 3 e 4 del foglio spaziotempo. L’evento, partire sia da 1 che da 2 e finire sia in 3 che in 4, può compiersi ovviamente, in molti modi. Noi però, conosciamo le ampiezze delle lettere corrispondenti e non abbiamo alcun problema a descriverli uno alla volta. L’evento ci ricorda quello che avevamo descritto con i fotoni per introdurre la moltiplicazione nel caso di un evento composto da due eventi che capitano in concomitanza, ricordate? Ma, allora, disegnavamo SOLO nello spazio, ora nello spaziotempo.

Iniziamo con le strade più semplici, come mostrato in Fig. 52(a).

Un elettrone parte da 1 e arriva in 3. L’altro elettrone parte da 2 e arriva in 4. L’evento è verificato. Qual è l’ampiezza di probabilità dell’evento completo seguendo questa strada? Basta moltiplicare tra loro le ampiezze dei due sotto-eventi. L’ampiezza finale per questa prima via è quindi data da E(1,3) x E(2,4). Banale direi? Ricordiamoci sempre, però, che dire da 1 a 3 vuole dire descrivere un numero incredibile di vie alternative con un numero enorme di possibili “step” intermedi e cambi di direzione. La freccia 1-3 è un simbolo per rappresentare tutta questa enorme serie di possibilità, che, tuttavia, sono tenute in conto nella formula che descrive E(1,3). Non lo diremo più, ma non pensiamo che la freccia da 1 a 3 indichi solo una strada dell’elettrone. Tuttavia, disegnandolo in questo modo, ogni elettrone non ha accoppiamenti lungo il suo percorso, comunque sia complicato e travagliato.

E’ immediato trovare una seconda strada altrettanto semplice: un elettrone parte da 1 e finisce in 4 e l’altro parte da 2 e finisce in 3 (Fig. 52(b)). L’evento è nuovamente verificato. Quanto vale la sua ampiezza di probabilità? Presto detto: E(1,4) x E(2,3).

Se volessimo fermarci qui, non ci resterebbe adesso che sommare vettorialmente le due ampiezze e avremmo l’ampiezza finale dell’evento. In linea di massima, l’ampiezza di probabilità ottenuta con queste due “ovvie” strade (e di conseguenza la probabilità che si verifichi l’evento) approssima più che bene la realtà dei fatti. Ci si potrebbe anche accontentare…? No, no, non scherziamo. Conosciamo benissimo le possibilità della QED e non possiamo fermarci a una prima “rozza” approssimazione: la Natura a volte è capricciosa e su spazi piccoli ne combina di tutti i colori. Dobbiamo andare avanti.

Finora abbiamo usato solo la seconda lettera dell’alfabeto (un elettrone va da un punto a un altro): è ora di introdurre anche le altre due. Presto fatto, basta aggiungere un fotone e due accoppiamenti elettrone-fotone. La nuova strada è descritta in Fig. 53(a)

Cosa succede? Il primo elettrone, giunto a un certo punto (se ne stava andando in una direzione veramente qualsiasi) emette un fotone e cambia direzione in modo da finire in 3. La stessa cosa fa il secondo elettrone. Anche lui subisce un accoppiamento. In questo caso, però, assorbe un fotone, proprio lo stesso emesso dal primo elettrone. Anche il secondo elettrone cambia direzione e finisce in 4. L’evento è verificato? Sicuramente sì, dato che gli elettroni sono giunti nei loro punti di arrivo. Notiamo che il fotone è apparso ed è sparito prima della conclusione dell’evento. Notiamo anche la differenza tra la possibilità dell’elettrone di cambiare percorso quante volte vuole (fatto richiamato nella figura precedente) e l’introduzione di un punto di accoppiamento. Non sono la stessa cosa, dato che nel secondo caso esiste una particolare ampiezza da associare a quel punto, indicata dal numero j.

Vogliamo calcolare l’ampiezza di probabilità finale di questo modo di verificare l’evento? Non è troppo difficile, anche se un po’ noioso. Non ci resta che moltiplicare tra loro le ampiezze di ogni azione svolta (le lettere) per completare l’evento. Scriviamo insieme questa moltiplicazione, ricordandoci che esiste anche il tragitto del fotone da 5 a 6. Non possiamo dimenticarcelo anche se il fotone ha solo fatto una fugace apparizione.

E(1,5) x j x E (5,3) x E(2,6) x j x E(6.4)x P(5,6)

Un bel pasticcio, pieno di accorciamenti e di rotazioni, che non vogliamo certo descrivere in dettaglio. Ormai c’interessa solo l’ampiezza di probabilità finale. Ricordiamoci, inoltre, che E e P sono espressioni matematiche non certo facili da scrivere. Tuttavia, noi lavoriamo solo graficamente, un’azione veramente elementare utilizzando le lettere di Alice. Conoscendo le ampiezze relative, la moltiplicazione ci permette di scrivere perfettamente la prima parola. Il risultato finale è stato ottenuto quasi ridendo e adesso ai “teorici” non resta che trasformarlo nuovamente in termini matematici. Anche loro, però, ne hanno approfittato, dato che non hanno dovuto fare tutti i conti intermedi, che sono stati sostituiti da poche linee tracciate su un foglio (ma quel foglio particolare, mi raccomando!).

Non è certo difficile inventarsi un’altra strada che verifica l’evento, come ad esempio mostra la Fig. 53(b). Siete sicuramente in grado di scrivere da soli l’espressione dell’ampiezza finale di questa strada e vi invito a provarci.

Cosa abbiamo trovato? Beh… che le due nuove strade portano anch’esse alla realizzazione dell’evento e non sono assolutamente distinguibili dalle prime due della Fig. 52. Ognuna è una strada plausibile che ha una sua ampiezza di probabilità di essere seguita. E’ quindi è più che giusto sommarle vettorialmente alle prime due in modo da approssimare sempre meglio la probabilità totale dell’evento che, ricordo ancora, dice soltanto: due elettroni partono da 1 e 2 e finiscono in 3 e 4.

Attenzione a non dimenticarci che i punti 5 e 6 possono essere ovunque nello spazio-tempo e che spostando loro cambiano di conseguenza le espressioni che forniscono l’ampiezza di ogni nuova strada. Nuova strada vuol dire una nuova ampiezza finale alternativa da aggiungere a quelle precedenti. Un lavoro incredibilmente lungo e laborioso per essere completato manualmente!

Il fatto che 5 e 6 possano trovarsi ovunque, però, ci obbliga a fare un’importante riflessione a cui avevamo già accennato.

Se il punto 6 ha una coordinata tempo più grande di quella di 5 (ossia se il punto 6 è successivo al punto 5) preferiamo dire che il fotone è emesso in 5 e assorbito in 6. Se, invece, il punto 6 precede 5, preferiamo dire che il fotone è emesso in 6 e assorbito in 5. Tuttavia, potremmo anche dire, nel secondo caso, che il fotone è emesso in 5 e assorbito in 6, andando indietro nel tempo. Nel foglio di Alice niente è impossibile e quindi è meglio dire, in generale, che il fotone è stato scambiato dai due elettroni. A questo fotone così scambiato, che in realtà appare e scompare durante l’evento, viene dato il nome di fotone “virtuale”.

Niente a che vedere con i fotoni virtuali che avevamo introdotto per cercare di esprimere il concetto relativo alla posizione qualsiasi che può assumere un fotone una volta che è partito da una sorgente. Notate anche che non ci siamo certo preoccupati di vedere come è inclinata la retta descritta dal fotone “virtuale”: può anche non essere a 45° e quindi muoversi a velocità diversa da c.

Vale la pena disegnare la Fig. 54, che illustra meglio questa situazione apparente assurda, ma del tutto ammissibile nel quaderno di Alice.

A sinistra (a) il caso più semplice: il fotone va nel verso giusto del tempo, anche se la sua velocità è maggiore di quella convenzionale. Nel secondo caso (b) il fotone è emesso e assorbito nello stesso istante (velocità infinita?). Nel terzo caso (c), la luce sembra andare secondo la sua velocità “normale”, ma lo fa nel verso opposto del tempo! Niente di strano, amici miei: siamo o non siamo nel regno dello Stregatto e del cappellaio matto? Possiamo dire che le ampiezze di probabilità che stiamo usando tengono conto di tutte queste possibilità e non vi è nessun problema a eseguire calcoli che sembrerebbero assurdi. In fondo, non fanno altro che seguire la Natura, dato che si ottengono proprio i suoi risultati!

Ci sembra di aver complicato abbastanza le cose? Nemmeno per sogno. Lo stesso evento ha infinite altre possibilità di verificarsi. Basta, ad esempio, aggiungere due ulteriori punti (7 e in cui avviene un nuovo scambio di un fotone virtuale tra i due elettroni. La Fig. 55 non è certo complicata, ma… le moltiplicazioni cominciano a diventare pesanti… anche perché 5,6,7,8 possono essere ovunque. Milioni e milioni di vie alternative che si devono sommare. Mamma mia… Se volete, potete provare a scrivere l’ampiezza di probabilità di questa figura: è solo un lavoro di routine quantistica!

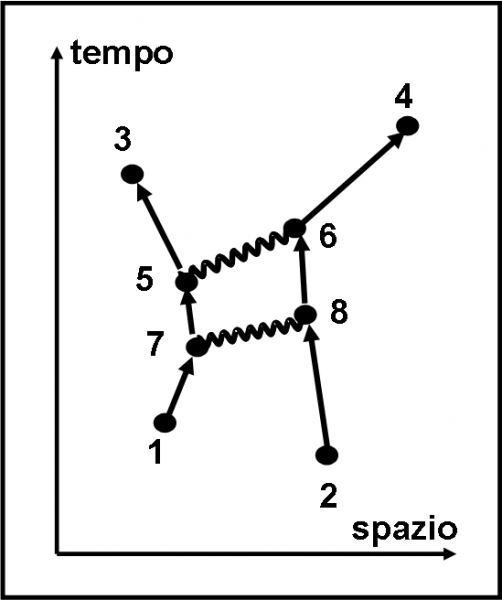
A mano a mano che continuiamo a complicare le cose, risulta evidente una particolarità che ci aiuta non poco. Le prime due strade considerate per verificare l’evento non fanno uso di accoppiamenti, ossia manca sia la seconda che la terza lettera dell’alfabeto. Ne consegue che non compare il numero “magico” j. Aggiungendo due punti intermedi e un fotone, compare il numero j x j. Nel caso dei quattro punti intermedi (due fotoni virtuali) il numero diventa j x j x j x j.

Ricordiamo, però, che ogni j implica un accorciamento dell’ampiezza a circa 0.1. La strada con due punti porta, quindi, a un’ampiezza ridotta a 0.1 x 0.1 = 0.01, rispetto a quella senza accoppiamenti. Con quattro punti l’ampiezza si riduce a 0.1 x 0.1 x 0.1 x 0.1 = 0. 0001 (ossia uno su 10000). Se avessimo tempo al computer potremmo arrivare fino al caso di  j ⁶, con tutte le possibili posizioni dei 6 punti aggiuntivi. Cosa stiamo imparando? Che questo metodo di calcolo della probabilità di un evento non ha nessun problema di arrivare fino a una precisione fantastica: basta continuare con una regola sempre uguale e oltremodo semplice concettualmente. Se mai ce ne fosse bisogno, una prova ulteriore della perfezione della QED.

Per cercare di rimanere con i piedi per terra, cosa significa ciò che abbiamo appena visto? Molto facile da tradurre in parole “comuni”: due elettroni si inviano un’informazione tramite un fotone. Quest’ultimo è il messaggero, un mediatore della forza che si esercita tra le due particelle che capiscono di doversi tenere a distanza. Due elettroni non possono attrarsi ma respingersi. Il fotone virtuale evita uno scontro “impossibile”.

Io  do un fotone a te e tu dai un fotone a me: lo scattering della luce

Presentiamo, ora, un altro evento descritto facilmente dal diagramma relativo. Iniziamo con un elettrone e un fotone e terminiamo ancora con un fotone e un elettrone. Tra le tante strade possibili per verificare l’evento, ce ne interessa una in particolare che introduce due volte la terza lettera. In realtà potevamo anche far continuare fotone ed elettrone senza alcun incontro, ma sarebbe  una strada di poco interesse scientifico, anche se molto più probabile. Nel caso prescelto l’elettrone assorbe il fotone e, dopo un po’, lo riemette di nuovo. L’evento è verificato e il diagramma descrive perfettamente quello che chiamiamo normalmente “scattering” della luce. Cominciate a capire la grandezza dei diagrammi di Feynman? Definite le ampiezze di probabilità delle tre lettere di base, la loro combinazione porta a descrivere tutti i fenomeni della Natura.

La Fig. 56 illustra il caso in oggetto: in (a) l’elettrone assorbe un fotone, continua da solo e dopo un po’ emette un altro fotone. L’evento è verificato dato che siamo partiti da un fotone e un elettrone, in un certo istante, e siamo arrivati ancora con un fotone e un elettrone, in un tempo successivo. Tuttavia, si possono presentare altre possibilità. In (b) l’elettrone emette prima un fotone e poi ne assorbe un altro. Come sappiamo, le due azioni sono equivalenti. In (c), però, le cose si complicano un poco (per noi almeno). L’elettrone emette un fotone, poi torna indietro nel tempo per assorbire un altro fotone e infine riprende il cammino normale. L’evento è verificato nuovamente, anche se abbiamo avuto bisogno di un’azione apparentemente molto strana (che però è tenuta in conto nella formula che rappresenta E(A,B)). Discutiamone un attimo.

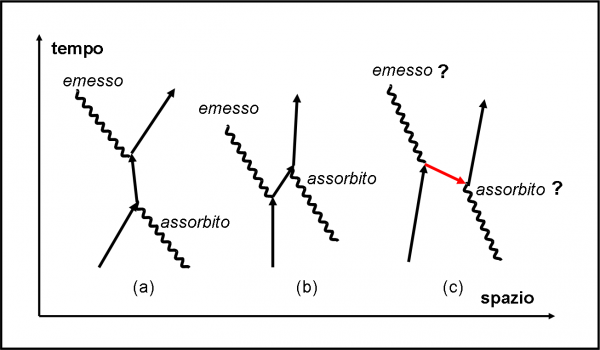
Antimateria

L’elettrone così “anomalo”  ha una caratteristica saliente, malgrado sia del tutto identico a un elettrone normale: esso viene attratto da quest’ultimo e si definisce come elettrone a carica positiva (se sviluppassimo la formula della probabilità tenendo conto della polarizzazione ce ne renderemmo conto attraverso il segno di j… ma è troppo per noi e accettiamo questo strano comportamento senza crearci problemi inutili). In altre parole, prende il nome di positrone o anti-elettrone. Ogni particella ha una sua anti-particella, tranne il fotone che è l’anti-particella di se stessa. Lo abbiamo già visto precedentemente, quando il fotone tornava indietro nel tempo, ma niente cambiava dato che emissione e assorbimento sono la stessa cosa. Quando un elettrone e un positrone si incontrano si annichiliscono dando origine ad almeno un fotone.

Ricordiamo solo che tutte le particelle, tranne appunto il fotone, hanno un’anti particella. Ogni riferimento all’antimateria NON è assolutamente casuale!

Si potrebbero usare due modi per indicare un positrone: o si lascia la freccia direzionale così com’è, accettando che sia un elettrone che va indietro nel tempo, o si cambia il senso della freccia direzionale, sapendo però che siamo di fronte a una nuova particella, il positrone appunto. Noi useremo la prima, dato che ci permette di vedere subito se la particella è a carica positiva o negativa: basta vedere se il suo verso è opposto o pure no a quello del tempo.

Sì, sì, tante belle parole… ma vorremmo capire come il diagramma di Feynman ci descrive queste azioni (confermate dagli esperimenti di laboratorio e quindi naturali). Riprendiamo la Fig. 56(c) e riproponiamola in Fig. 57, dividendola, per facilitare il discorso, in intervalli temporali (linee orizzontali).

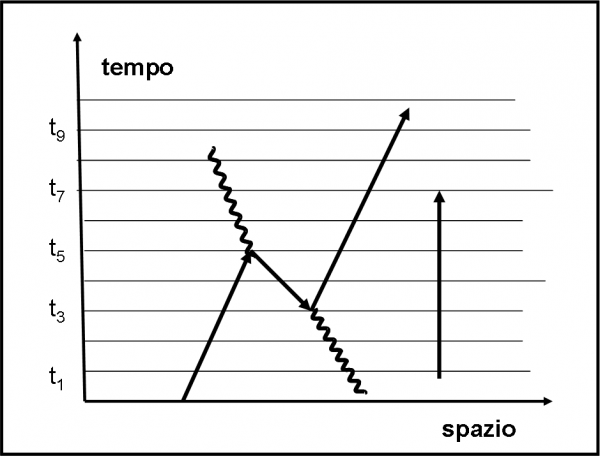
Muoviamoci nella direzione positiva del tempo, ossia verso l’alto, come siamo abituati a fare nel nostro mondo, non cercando di guardare troppo avanti, ma descrivendo quello che ci appare di volta in volta. In parole povere non sappiamo se un elettrone nel futuro ha assorbito o emesso un fotone ed è tornato indietro. Noi conosciamo quello che vediamo. In t₀ troviamo un elettrone e un fotone che si muovono uno verso l’altro nella giusta direzione temporale. Tutto prosegue normalmente fino a t₃, quando improvvisamente il fotone si trasforma in due particelle, un elettrone e un positrone (a prima vista potrebbe anche sembrare un elettrone, ma ha verso opposto). Il positrone continua la sua corsa, ma non riesce a vivere a lungo e si incontra con l’elettrone in t₅ (che è poi se stesso!) annichilendosi e dando origine a un fotone, che continua verso l’alto, così come sta facendo anche l’elettrone “creatosi” in t₃. In t₇ tutto è a posto: un elettrone e un fotone, come previsto dall’evento. Questa è una visione “normale” del fenomeno, che, però, può essere interpretato come un doppio accoppiamento secondo le regole generali esistenti nel piano di Alice, dove il verso del tempo non è assolutamente un ostacolo. L’evento che in questa visione è inteso come un’emissione, seguito da un assorbimento, nel tempo “comune” porta al fenomeno dell’annichilazione di un positrone e di un elettrone.

Ricordiamo ancora che questa sequenza è stata osservata in laboratorio ed è inserita nell’ampiezza E(A,B). Inoltre, teniamo conto che le anti-particelle sono rappresentate con un verso contrario a quello del tempo solo nel nostro foglio speciale. Non prendiamola come una “verità”: è solo un azione perfetta per il calcolo, ma del tutto simbolica. Siamo o non siamo nel mondo di Alice?

Un passo indietro

Forse siamo andati un po’ troppo veloci ed è meglio soffermarsi ancora sull’accoppiamento, ossia sulla terza lettera. Diciamoci la verità: se non ci fosse lei la Natura sarebbe veramente monotona e gli elettroni e i fotoni se ne andrebbero per i fatti loro senza mai incontrarsi. Anzi, ancora peggio, non ci sarebbero nemmeno gli oggetti, dato che le particelle non avrebbero modo di parlarsi e di formare atomi e cose sempre più complesse.

La terza lettera, quindi, è proprio il sale dell’Universo! Essa, da sola, può già mostrare i primi diagrammi di Feynman che descrivono fenomeni che ben conosciamo. Innanzitutto, essa è valida solo se vi sono tre linee incidenti, due per l’elettrone e una per il fotone. Dato che l’elettrone deve essere unico, non potremo mai avere due elettroni entranti nel “punto triplo”. L’elettrone deve proseguire il suo cammino senza curarsi se va dalla parte del tempo positivo o negativo. Nel primo caso tutto è normale; nel secondo si ha, in realtà, l’unione è l’annichilimento di un elettrone e un positrone. Questa è la sola regola da ricordarsi perfettamente. Ossia, non cerchiamo MAI di disegnare due elettroni che entrano nel punto d’accoppiamento. Questo è un fenomeno assurdo anche per il mondo d’Alice. D’altra parte è ovvio. Vorrebbe dire che due elettroni possono attrarsi! Eh no! Lo possono fare solo un elettrone e un positrone.

Vediamo in Fig. 58 alcuni casi di accoppiamento, di cui due sono assurdi anche per il mondo dell’assurdo.

La (a) ci mostra un elettrone che assorbe un fotone e continua indisturbato verso l’alto. Perché diciamo che il fotone è stato assorbito? Ovvio, perché esso scompare andando verso il tempo positivo. Una particella è stata “ingoiata"! Questo semplicissimo digramma corrisponde a qualcosa che conosciamo? Sicuramente sì. pensate a un’antenna radio che capta i fotoni in arrivo o a una lente o a un semplice pezzo di vetro, ecc., ecc.

In (b), invece, partiamo con un elettrone che nel punto critico tira fuori un fotone dal suo cappello. Abbiamo cominciato con una sola particella e finiamo con due. In questo caso si è creato un fotone e quindi è stato “emesso”. Conosciamo questo fenomeno? Beh… basta pensare ai colori! La (b) però potrebbe anche essere interpretata come assorbimento di un fotone particolare, ossia un fotone che torna indietro nel tempo. Dato che l’antifotone rimane se stesso la faccenda non ci sconvolge di certo e l’abbiamo già visto nel caso del fotone “virtuale” che permette a due elettroni di comunicare e di avvisarsi che è meglio tenersi alla larga uno dall’altro (Fig. 54).

Il caso (c) è quello apparentemente più strano. Si ottiene, però, attraverso semplici ribaltamenti di figura (non approfondiamo se no cadiamo nella simmetria CPT e non la finiremmo più). Anche in questo caso vi è l' elettrone entrante e  uscente, ma quest’ultimo va indietro nel tempo e quindi è un positrone. In realtà, quindi, abbiamo un elettrone e un positrone entranti nel punto di interazione. Seguendo il verso positivo del tempo, partiamo, quindi, con un elettrone e un positrone e finiamo solo e soltanto con un fotone. La particella e l’antiparticella hanno subito l’annichilimento.

Il caso (d) non è invece ammissibile. In esso si parte con due elettroni che convergono in un punto. No, impossibile e quindi la terza lettera è stata scritta in modo errato. La stessa cosa capita in (e) dove compare un solo elettrone e due fotoni. No, niente da fare. Rimandati a settembre!

Bene, direi che l’interazione o accoppiamento sia stato analizzato da ogni parte e non dovremmo più avere problemi a comprenderla nei diagrammi più complicati. Ci ha anche permesso di descrivere come compare l’antimateria nel mondo di Alice: è solo questione di direzione, dato che nel nostro foglio speciale si può andare dove si vuole rispetto al tempo.

Qualcuno starà, forse, pensando alle leggi di conservazione… Infatti, abbiamo visto che si distruggono e si creano particelle dal niente. Si parte con una e si arriva a due e viceversa. Anzi può capitare molto di peggio con diagrammi più complicati come vedremo tra un attimo. Nessuna paura. La matematica risolve tutti i problemi relativi (fidatevi), ma nei diagrammi l’importante è che si conservi la “carica” totale delle particelle. Se, in un vostro diagramma doveste trovare che la carica è cambiata… fermatevi perché avete commesso un errore.

Tanto per prendere dimestichezza (ma senza spiegare cosa significhi) ecco, in Fig. 59, un diagramma molto più complesso (l’avremmo potuto disegnare a tentativi, per divertimento). Contiamo le cariche all’inizio: due elettroni veri, ossia due cariche negative. Vediamo cosa troviamo alla fine: tre elettroni e un positrone, ossia tre cariche negative e una positiva, ossia due cariche negative. Perfetto. Il diagramma ha sicuramente un senso e rappresenta un processo della Natura. Questa è la grande forza dei diagrammi di Feynman.

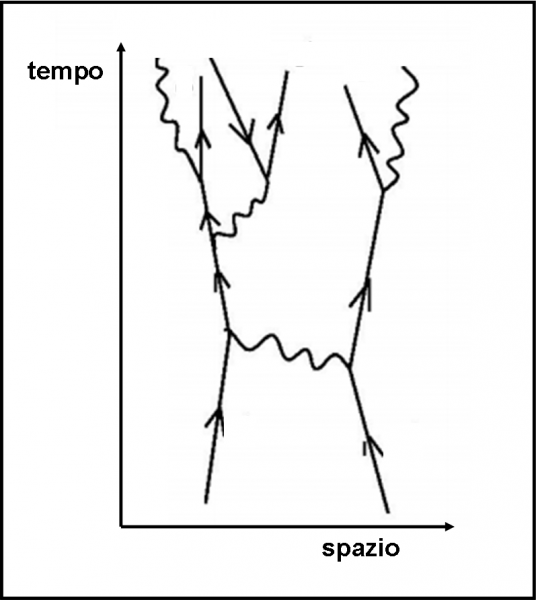
Teoricamente potremmo inventarci qualsiasi disegno, più o meno complicato, ma se rispettiamo le poche regole che conosciamo e se le cariche si conservano, siamo SICURI di aver rappresentato un fenomeno naturale, qualunque sia la sua ampiezza di probabilità di accadere (a quello ci pensano le ampiezze che si moltiplicano). E non dobbiamo nemmeno preoccuparci di quante particelle vi sono all’inizio e alla fine. Nel caso della figura partiamo con due e arriviamo addirittura a sei (oltre ad avere avuto un fotone virtuale durante il percorso).

Fermiamoci un attimo con un momento di auto soddisfazione. Pensate, cari amici, che potreste facilmente costruire da soli diagrammi anche più complicati di quello appena mostrato. Basterebbe stare bene attenti al verso delle frecce e contare le cariche. A quel punto, in pochi minuti, avreste sottomano un fenomeno naturale che, per poter essere descritto matematicamente passo dopo passo, avrebbe avuto bisogno di una preparazione superiore e/o un tempo enorme al supercomputer. Invece, in pochi minuti si ottiene un risultato SICURAMENTE plausibile e possibile.

Basta, a questo punto, dare il vostro disegno a un matematico con i fiocchi (non a me…) e fargli trasformare il diagramma in linguaggio matematico. Vi darà la soluzione, evitando tutti i passaggi intermedi. Capite che meraviglia la QED? Un premio Nobel per la fisica quantistica potrebbe anche avere un assistente bambino (un po’ sveglio e riflessivo). Il giovane disegnerebbe diagrammi a piacere e lo scienziato non dovrebbe far altro che riscriverli con le formule relative, interpretarli e magari chiedere ai tecnici del CERN di effettuate un certo esperimento che verifichi quanto disegnato allegramente dal mini-assistente.

Va bene… ho un po’ scherzato, ma non poi tanto…

La casa dell’elettrone

Abbiamo parlato di elettroni, considerandoli liberi di muoversi a loro piacimento, quasi come fossero dei… fotoni. In realtà, la situazione è piuttosto diversa. Gli elettroni sono normalmente (nei fenomeni più comuni) legati a un peso non trascurabile. In altre parole… hanno sempre una palla al piede che li tiene ancorati a un  qualcosa. Quel qualcosa è il nucleo atomico, dove si rifugiano i protoni e i neutroni, a loro volta “casa” di particelle ancora più piccole.

Feynman chiama il protone il “vaso di Pandora”: guai ad aprirlo! Al livello raggiunto finora possiamo permetterci di non complicare troppo le cose e considerare il nucleo atomico come una singola particella in quiete, ossia priva di movimento spaziale. Anche a lui si associa, ovviamente, un’ampiezza di probabilità di andare da un punto a un altro e l’espressione è del tutto simile alla E(A,B) dell’elettrone, solo che contiene un numero maggiore di “n” (ricordate?). Il nucleo è però ben più “pesante” dell’elettrone e non commettiamo un grave errore se lo consideriamo fermo.

Sempre per motivi di semplicità riferiamoci all’atomo più semplice, ossia a quello dell’idrogeno. Il nucleo si riduce a un protone ed è presente un solo elettrone. La Fig. 60 illustra il diagramma spazio-temporale di questo atomo.

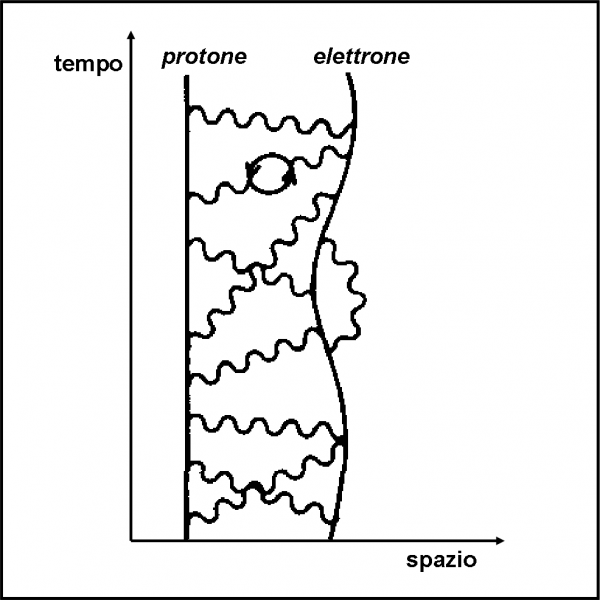
La linea verticale rappresenta il protone (non si muove nello spazio), mentre la linea ondulata è l’elettrone, che scalpita, ma che viene trattenuto a una certa distanza da un continuo scambio di fotoni virtuali con il protone. Un messaggio continuo, una mediazione della forza che tiene unito l’atomo. Un vero e proprio balletto che l’elettrone compie “attorno” al nucleo. Ovviamente, se il nucleo è composto da più protoni, gli elettroni aumentano e il diagramma corrispondente si complica in modo mostruoso, ma non per questo cessa di essere rappresentabile con le solite regole della QED. Ricordiamoci che le lettere dell’alfabeto rimangono solo e soltanto tre.

L’ampiezza di un fotone che viene scambiato tra protone ed elettrone è semplicemente (–j) x P(A,B) x j. In altre parole, l’ampiezza di un fotone che va da un punto a un altro, moltiplicata per le ampiezze dei due accoppiamenti. Il segno meno di j definisce quello relativo all’accoppiamento protone-elettrone. Non preoccupatevi di un fotone che esce ed entra nello stesso elettrone e nemmeno di quello strano cerchietto che individua la nascita e la morte simultanea di un positrone: possiamo trascurarli (almeno per adesso).

Se quello precedente è il diagramma relativo al mantenimento di un elettrone nei pressi del protone, non è difficile disegnare lo “scattering”  della luce quando l’elettrone è ancorato al suo atomo.  Lo vediamo in Fig. 61.

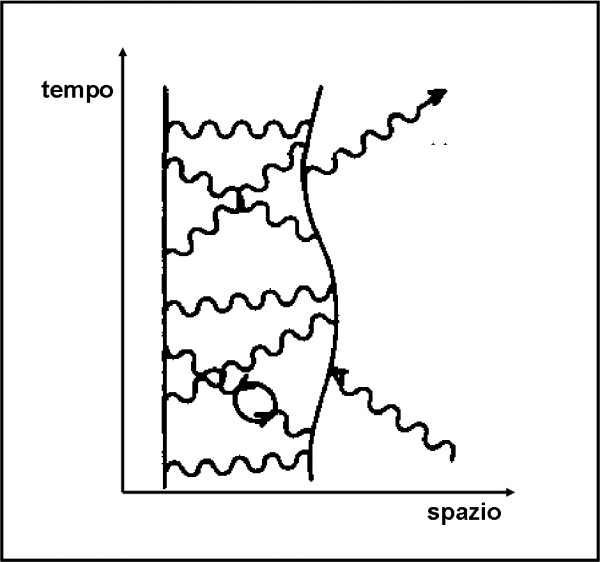
Mentre continua ad avvenire il continuo scambio di fotoni, un fotone estraneo può facilmente colpire l’elettrone ed essere assorbito. Dopo poco tempo, l’elettrone “sputa”un nuovo fotone, dando luogo al fenomeno di scattering. Può anche capitare (e l’abbiamo già visto) che l’elettrone emetta prima un fotone e poi l’assorba. Le varie combinazioni danno luogo a tutti  i fenomeni di scattering che conosciamo.

Possiamo concludere questa rapida analisi dell’atomo con una constatazione veramente semplice: l’ampiezza di probabilità di avere uno scattering (di qualsiasi tipo sia) è data da una serie di rotazioni e accorciamenti che può essere definita come Sc. Sapremmo benissimo (non è un vero problema) scrivere quest’ampiezza, che dipende, ovviamente, dal nucleo e da come si sistemano gli elettroni vicino a lui. In parole semplici, l’ampiezza varia da materiale a materiale. Finora ci siamo soprattutto “fissati” sul vetro (e continueremo a farlo), ma ogni materiale ha la sua propria ampiezza di scattering.

Un piccolo commento prima di proseguire: vi siete accorti come è diventato banale e intuitivo disegnare (qualitativamente) un atomo e le interazioni tra nucleo ed elettrone? Per non parlare dei fenomeni di scattering e di interazione elettromagnetica. Sì, d’accordo, per passare alla quantificazione è necessario tradurre tutto in formule matematiche, ma praticamente non vi sono problemi concettuali, dato che ogni lettera ha una sua ben definita ampiezza di probabilità. Basta solo moltiplicare e sommare, operazioni alla portata di chiunque… Potrei permettermi di dire che più si va avanti e più le cose sembrano semplificarsi. Lo stesso succede a scuola: è molto più difficile scrivere le prime lettere dell’alfabeto che, una volta imparatele molto bene, iniziare a scrivere delle parole e delle frasi a senso compiuto.

Un cronometro fittizio

Penso che uno dei concetti, che ci ha “disturbato” di più, sia stato quel cronometro che, associato a una freccia, la faceva girare in modo diverso a seconda del colore della luce. La sua importanza è fondamentale, dato che la direzione della lancetta ci permette di sommare o di eliminare ampiezze di pari lunghezza. Un po’ come fa la velocità con l’accelerazione. Due velocità uguali possono dar luogo a un’accelerazione diversa da zero (il moto circolare uniforme ce lo insegna).

Dover vedere questa caratteristica così importante rappresentata da un cronometro astratto che non esiste in Natura è una fatica mentale che viene mal sopportata anche nel mondo di Alice.  Ormai, però, siamo in grado di svelare cos’ è veramente questo cronometro e come funziona. Lo possiamo fare perché non ci spaventano più i diagrammi spazio temporali (almeno spero…).

Prima di iniziare, ricordiamoci ancora una volta di non confondere traiettorie spazio temporali con traiettorie soltanto spaziali. Quando avevamo illustrato la riflessione e la doppia riflessione, usavamo traiettorie inclinate. Può anche darsi che qualcuno abbia confuso, saltuariamente, gli angoli indicati dalla lancetta del cronometro con gli angoli fatti dalle traiettorie. Adesso, questo non è più possibile, dato che lo spazio si è ridotto a una retta e quindi tutti i movimenti spaziali avvengono su di essa. Rimane, invece, inalterata la direzione della freccia-ampiezza e l’angolo ad essa relativa. Le traiettorie che vedremo indicheranno, d’ora in poi, percorsi immaginari nello spaziotempo, l’unico foglio in cui possono essere rappresentate le tre lettere di Alice.

Per svelare il mistero del cronometro, pensiamo un attimo a come abbiamo definito l’ampiezza P(A,B) del viaggio di un fotone da un punto a un altro. Abbiamo parlato di rotazione della freccia? Assolutamente no. Eppure, andare da A a B vuol proprio dire partire dalla sorgente e giungere in un certo luogo (lo specchio, il vetro, il rivelatore). Si è sempre detto che durante questo viaggio spaziale il cronometro continua a girare e adesso, improvvisamente, non ce ne importa più niente e concludiamo che passare da A a B non comporta nessuna rotazione della freccia-ampiezza P(A,B).

Forse qualcuno ci aveva già pensato e aveva trovato questo confronto del tutto assurdo, anche per il mondo di Alice. E avrebbe avuto sicuramente ragione. Non possiamo più nasconderci dietro la rappresentazione ingenua e simbolica del cronometro.

L’angolo della ampiezza, infatti, non dipende dallo spazio percorso e dal tempo impiegato a percorrerlo, ma solo e soltanto dall’istante in cui la luce lascia la sorgente. Ma come?! Ci crolla il mondo addosso (quello normale). Tanta fatica a parlare di differenza di traiettoria e adesso la trascuriamo completamente?

Pensiamo un momento a ciò che succederebbe se la rotazione dell’ampiezza venisse impartita subito, all’inizio del viaggio. Se le frecce partissero tutte assieme avrebbero tutte la stessa direzione. Niente e nessuno la potrebbe cambiare senza incontri strani durante il percorso. Che una freccia faccia un percorso più lungo o più corto non potrebbe modificarla. Tuttavia (state bene attenti!), esse viaggiano alla stessa velocità e, quindi, se voglio ricevere la luce di due fotoni sullo stesso rivelatore allo stesso medesimo istante (quello che capita in realtà), devo considerare, per loro, tempi di partenza diversi. Solo tempi di partenza diversi danno angoli diversi alla freccia.

Tuttavia, se voglio che due fotoni partano in tempi diversi (angolo di ampiezza diverso) e arrivino contemporaneamente nello stesso punto, è necessario che uno dei due faccia un percorso più lungo o più corto. In caso contrario (ossia percorsi spaziali uguali),  dato che la loro velocità è costante (e la possiamo considerare uguale a c su lunghe distanze),  uno dei due arriverebbe o prima o dopo l’altro. Da questa conclusione non si scappa neanche nel mondo di Alice.

Insomma, tempi di partenza diversi e arrivi simultanei implicano anche percorsi diversi: i due metodi di calcolo dell’angolo sono perfettamente equivalenti.

Non confondetevi… sto dicendo una vera banalità. Se due atleti vanno alla stessa velocità e voglio vederli arrivare sul traguardo nello stesso istante, facendoli partire in tempi diversi, è necessario che uno dei due faccia un percorso più lungo.  O, inversamente, se voglio che arrivino insieme, ma hanno davanti percorsi diversi, è necessario che partano in tempi diversi. Le due cose sono perfettamente uguali. Da questa semplice riflessione se ne deduce che non abbiamo commesso nessun errore finora a far girare la lancetta del cronometro: il risultato finale è lo stesso. Tuttavia, lo spaziotempo e le lettere del nuovo linguaggio ci permettono, adesso, di essere un po’ meno assurdi nel mondo dell’assurdo.

Ancora la doppia riflessione (che barba!)

Bando alle ciance e a tante parole, vediamo cosa capita in realtà. L’evento da descrivere è: “Parti da S e arriva in R, a un certo istante, dopo la riflessione  su una lamina di vetro ”. Come si vede, non parliamo più di doppia riflessione… non c’è più bisogno di semplificazioni artificiose (lo vedremo meglio tra poco). L’evento è, però, sempre lo stesso, lo conosciamo molto bene.

Iniziamo con analisi accurata della sorgente S. Restiamo nell’ambito di luce monocromatica, ossia di un solo colore. In queste condizioni, l’ampiezza di probabilità che un fotone venga emesso varia in modo regolare col tempo. In particolare, varia in modo regolare l’angolo della freccia. Cambiando colore, cambierebbe la velocità di variazione. Esattamente ciò che faceva il nostro cronometro “fittizio”. Se la luce fosse un mix di colori (ad esempio luce bianca) l’angolo cambierebbe in modo caotico, senza alcun regolarità. Nel caso di luce monocromatica, invece, è possibile sapere perfettamente come avviene la rotazione della freccia e quindi conoscere l’ampiezza di probabilità.

La faccenda è molto semplice: l’angolo varia  a velocità costante, esattamente come faceva quello della lancetta del cronometro, ma andando in senso inverso. La Fig. 62 ci mostra la situazione relativa alla sorgente S. Essa, ovviamente, non si muove e descrive, perciò, una retta verticale. In istanti successivi facciamo partire un fotone che descrive la sua traiettoria verso il rivelatore. La lunghezza della freccia di probabilità è sempre la stessa, ma l’angolo gira in verso antiorario, come illustrato nella parte sinistra del grafico. Notate che le traiettorie spazio temporali dei fotoni sono parallele, dato che su distanze grandi la velocità della luce può essere considerata costante e uguale a c (angolo di 45°).

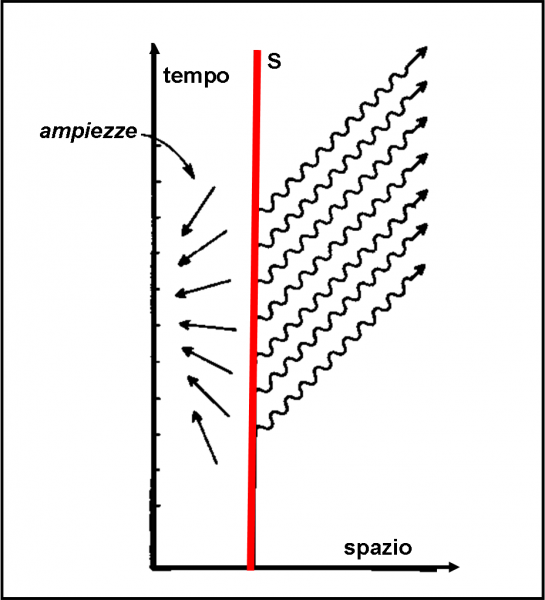
La luce è ora partita e viaggia verso la lamina di vetro. Non vi è più nessun cronometro e l’angolo dell’ampiezza rimane immutato fino al momento dell’incontro con il nuovo materiale. Non mi picchiate! Ricordo ancora che il viaggio e l’incontro successivo avvengono nello spaziotempo e NON nello spazio come nei capitoli iniziali. Nello spazio attuale, tutto avviene lungo una direzione orizzontale costante.

Questa volta, ci conviene partire dal rivelatore R. L’importante, ricordiamolo bene, è che la luce emessa in tempi diversi arrivi allo stesso istante T. Questo fatto, come abbiamo già visto prima, è fondamentale. In quel momento il rivelatore deve fare “tic”. Lui riceve un solo fotone, ma la sua ampiezza di probabilità dipende dall’ampiezza di probabilità di tanti ipotetici “fotoni” inviati in tempi diversi da S. Capiamoci bene, però. E’ la solita vecchia storia che il fotone diventa fotone solo quando arriva, mentre prima è solo un ampiezza di probabilità.  Poco sopra avevo parlato di fotoni che partivano e arrivavano, solo per rendere più “comprensibile” la faccenda. In verità la situazione è ben diversa. A ogni istante ciò che parte da S sono ampiezze di probabilità che solo alla fine si combinano tutte assieme per descrivere la probabilità di avere un “tic” in un certo istante.

L’evento dice esattamente questo: “La luce parte da S, ma deve arrivare in R al tempo T” non una frazione di tempo prima o dopo. Vogliamo soltanto calcolare la probabilità che ha un fotone partito da S di arrivare in R al tempo T, ossia di fare “tic”. Quanto tempo ha a disposizione la sorgente per tentare di far accadere l’evento? Dipende… Da cosa? Dallo spessore della lastra di vetro, come vedremo prestissimo.

Ancora un attimo di pazienza… Finora abbiamo parlato di doppia riflessione della luce su una lamina di vetro e ci siamo limitati alla riflessione su due sole superfici, quella superiore e quella inferiore. In realtà ciò non è vero e adesso siamo in grado di dire veramente le cose come stanno. Ogni atomo di vetro concorre al fenomeno, in particolare i suoi elettroni. Essere capaci di descrivere lo scattering della luce con le nuove lettere ci permette di parlare seriamente e di evitare semplificazioni inutili. Le superfici non hanno alcuna importanza particolare.

Tutto il processo viene gestito dagli elettroni interni al vetro che continuano ad assorbire fotoni e a riemetterli. Tuttavia, il risultato è esattamente lo stesso, per cui la divisione in due superfici continua a essere un procedimento più che valido. Solo che tra poco sapremo perché possiamo permetterci di eseguire questa semplificazione.

Disegniamo la Fig. 63 e non spaventiamoci. Sembra complicata ma non lo è. Basta descriverla e seguirla con molta calma. Dividiamo la lamina di vetro in un certo numero di straterelli (sei, ad esempio). Facciamo anche una premessa. Da quanto abbiamo dedotto nelle prime lezioni, sappiamo che la luce è soprattutto riflessa nella parte mediana della lamina di vetro. Non solo, però. Sappiamo anche che la direzione che può prendere è o verso il rivelatore R1 o verso l’interno della lamina. Per ottenere questo risultato avevamo sommato frecce relative a percorsi diversi. Ricordate? Bene, questo risultato vuole anche dire che lo scattering della luce che c’interessa è quello che emette fotoni in una di queste due direzioni. Tutte le altre possibilità, quando vengono combinate, danno una freccia finale nulla.

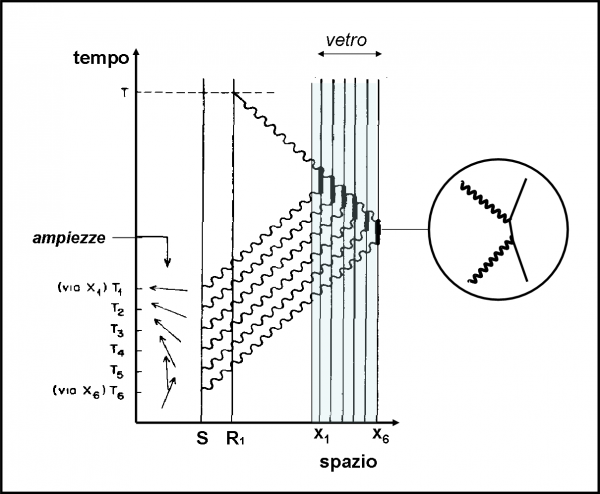
Possiamo perciò semplificare la figura, considerando come ampiezze da sommare alla fine solo quelle che colpiscono i punti mediani relativi a ogni straterello  (da x₁ a x₆).  (Nota Bene: devo ammettere di aver commesso una piccola inesattezza nelle Fig.  63 e 63bis  ( e lo commetterò anche per quella relativa alla trasmissione della luce). Per semplicità di disegno ho sempre fatto avvenire lo scattering nella parte terminale degli straterelli.  In realtà era meglio utilizzare un punto medio, ma… fatico già abbastanza a fare tutte queste figure e spero mi perdoniate… L’importante è saperlo).

Ovviamente, avremmo una precisione maggiore aumentando il numero di strati. Mi raccomando, non fissatevi sull’angolo delle traiettorie incidenti: esso non è assolutamente l’angolo di incidenza, ma rappresenta solo la velocità della luce c costante.  Quello che conta è solo la posizione dei punti all’interno  della lastra di vetro: la figura “spaziale” in due dimensioni è quella di Fig.  63bis e i punti sono situati tutti sulla verticale, linea mediana tra sorgente e rivelatore.

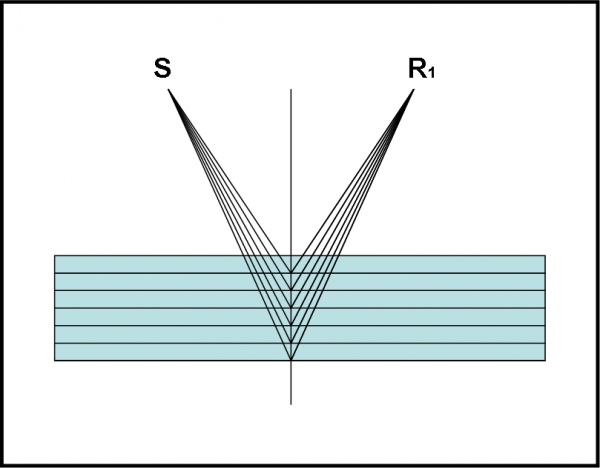
Torniamo alla Fig. 63 e iniziamo a calcolare le ampiezze lungo le traiettorie spazio-temporali che toccano i sei punti considerati. Sono quelle che permettono di finire in R1 nello stesso istante T. Capisco che può sorgere qualche difficoltà, ma cercate di estraniarvi più che potete dalla solita visione a due dimensioni spaziali. Le traiettorie sono solo e soltanto dei diagrammi di Feynman  relativi allo scattering della luce, come mostrato nel cerchio a destra della figura (lo riconoscete?). Le ampiezze delle loro probabilità permettono di calcolare la P(S,R1) di ogni diagramma attraverso la moltiplicazione delle parti in cui vengono divise, tenendo anche conto delle rotazioni relative ai punti di accoppiamento. Avremo una P(S,R1) per ogni traiettoria e alla fine potremo sommarle vettorialmente. In fondo, è sempre lo stesso procedimento che abbiamo già usato numerose volte.

Ogni singolo tragitto (da x₁ a x₆) può essere diviso in quattro “step”:

(1) un fotone è emesso dalla sorgente in un certo istante

(2) il fotone va dalla sorgente a un certo punto x del vetro

(3) nel punto x avviene lo scattering da parte di un elettrone

(4) il nuovo fotone raggiunge il rivelatore

Stiamo parlando di fotoni, ma sappiamo benissimo cosa intendiamo: l'ampiezza di probabilità che un fotone segua quella particolare traiettoria per finire in R1 al tempo T.

I passi (2) e (4) non causano assolutamente niente. La traiettoria si svolge nell’aria e nel vetro, ma l’ampiezza di probabilità non subisce né accorciamenti né rotazioni (a parte l’indebolimento dovuto alla distanza da percorrere, ma in questo caso interessa poco dato che è uguale per tutte le frecce).

Si può, infatti, assumere che tutta la luce segua il percorso tracciato, senza perdite o dispersioni (come indicano, in fondo, i diagrammi “simbolici” di Feynman nei tratti rettilinei).

Il passo (3) è lo scattering vero e proprio e implica accorciamento e rotazione, ma è una costante che dipende dal tipo di materiale, ossia il vetro. L’abbiamo chiamata Sc all’inizio del capitolo. Esso dà sicuramente luogo a un certo accorciamento e a una rotazione in senso orario che per il vetro risulta essere di 90°.

Il passo (1) è invece decisivo, dato che ogni traiettoria inizia a un tempo diverso e, di conseguenza, la freccia è diretta in una direzione variabile con regolarità (luce monocromatica). In poche parole, il passo (1) esegue in un istante quello che il vecchio “cronometro” faceva lungo la traiettoria. Se guardiamo la Fig. 63 vediamo benissimo che la distanza percorsa della luce nelle varie traiettorie è più piccola per x1 e più lunga per x6. Succede proprio quello che avevamo detto poco fa: per arrivare tutti assieme è necessario che chi fa il percorso più corto parta per ultimo e chi fa il percorso più lungo parta per primo.

Moltiplicando le ampiezze dei vari passi, otteniamo, quindi, frecce tutte accorciate della stessa lunghezza e tutte girate di 90° (a causa dello scattering nel vetro). Le differenze tra le loro direzioni rimangono identiche a quelle relative agli istanti in cui hanno lasciato S. Non ci resta che sommarle com’è rappresentato in Fig. 64. A sinistra abbiamo le sei frecce iniziali, come erano disegnate nella Fig. 63. Per non complicare la figura, abbiamo eseguito l’accorciamento e la rotazione (freccetta rossa) solo per la numero 1. Le frecce finali di ogni traiettoria vengono sommate vettorialmente nella parte destra, ottenendo l’ampiezza finale della probabilità che ha un fotone, partito da S, di colpire il rivelatore al tempo T.

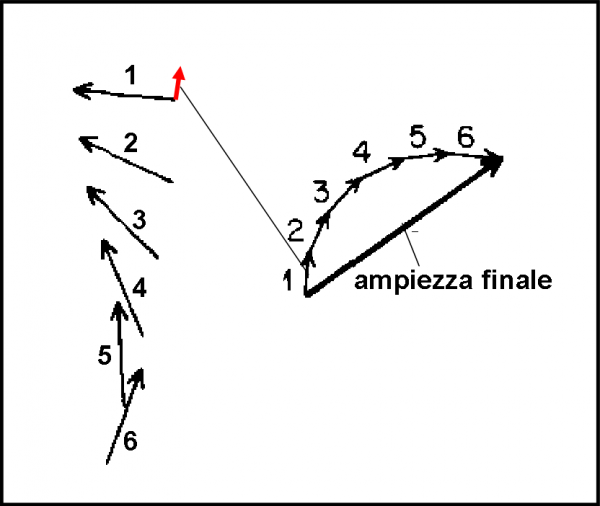
Ancora un piccolo sforzo e finiamo questo “terribile” esempio. Le frecce seguono un tratto di circonferenza, di cui la freccia finale è la relativa corda. E facile intuire che quando il tratto di circonferenza diventa esattamente la metà della stessa, la corda non è altro che il diametro. Essa è anche il valore massimo dell’ampiezza di probabilità. Poi la corda inizia ad accorciarsi per arrivare a zero quando si chiude la circonferenza. Questa variazione dipende dal tempo tra la prima e l’ultima traiettoria, ossia dallo spessore del vetro.

Un piccolo accenno alla realtà quotidiana: non vi sarà certo sfuggito il perfetto accordo con la “classica” lunghezza d’onda. Il periodo per compiere un intero giro della freccia è proprio la lunghezza d’onda divisa per la velocità della luce. Lo spessore del vetro, che porta a un giro completo della freccia, è proprio la lunghezza d’onda…

Torniamo a noi e vediamo perché avevamo potuto ridurre il tutto a due sole riflessioni (superficie superiore e inferiore), con quello “strano” ribaltamento della freccia per la prima riflessione e non per la seconda. Era solo un semplice “trucco”… Dimostriamolo con la Fig. 65.

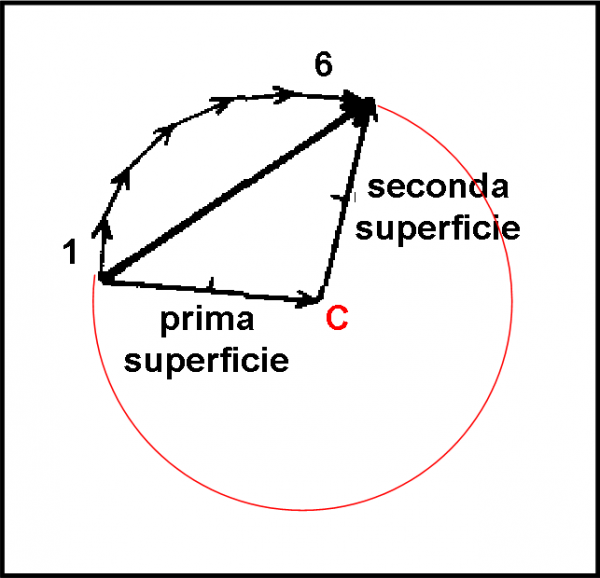
Consideriamo la stessa situazione precedente e individuiamo il centro C della circonferenza descritta dal’ampiezza. Tracciamo i due raggi che contengono la corda. Possiamo dire, con tranquillità, che la somma vettoriale dei due raggi è uguale alla corda, ossia all’ampiezza finale. Tuttavia, per poter sommare questi due raggi, è necessario invertire il verso del raggio che dal centro arriva all’inizio della freccia 1. Quello che va dal centro alla fine della freccia 6 rimane invece immutato. Cosa concludiamo? Per ottenere l’ampiezza finale basta sommare il primo raggio ribaltato e il secondo lasciato inalterato.

Considerando il primo come la freccia della prima riflessione e il secondo come quello della seconda riflessione, il gioco è fatto! Non commettiamo nessun errore, dato che il diametro del cerchio ha un’ampiezza di 0.4 (come si determina attraverso calcoli ed esperimenti). Ogni raggio vale, quindi, 0.2, proprio il numero magico che dava luogo alle ampiezze che variavano da 0 a 0.4 (e alle probabilità finali dallo 0 al 16%).

Nei capitoli iniziali, abbiamo potuto falsificare la situazione assumendo che la riflessione attraverso una lastra di vetro avvenisse solo nella prima e nella seconda superficie, dando luogo a due frecce di ampiezza uguale a 0.2 che si combinavano tra loro. La prima, però, doveva essere ribaltata di 180°.

In realtà, abbiamo visto che tutto si verifica “quantisticamente” attraverso lo scattering della luce in ogni punto della lamina. Possiamo quindi concludere che  la riflessione parziale di una lastra di vetro dipende solo e soltanto dallo scattering della luce all’interno del vetro. Tutto si riduce a una parola semplicissima dell’alfabeto che abbiamo imparato da poco. E la stessa cosa capita per qualsiasi fenomeno legato alla luce e alla sua interazione con la materia.

Appendice (facoltativa) per i più curiosi

Qualche parola in più sul valore 0.4 dell’ampiezza finale. Il raggio della circonferenza dipende essenzialmente dall’ampiezza delle singole freccette che lo descrivono. Quest’ultima dipende dall’ampiezza Sc che ha un elettrone del vetro di produrre un’azione di scattering. Lo scattering, però, non è altro che una parola dell’alfabeto di Alice-Feynman, formata dalle tre uniche sue lettere. Con le formule a disposizione e tenendo conto di tutte le possibili strade che permettono tale azione si può arrivare al valore del raggio della circonferenza. Per sostanze semplici, il calcolo non è impossibile, mentre per sostanze più complesse (come il vetro, ad esempio) sono stati necessari esperimenti di laboratorio. In realtà, il valore di 0.2 approssima molto bene la riflessione che avviene con la luce che colpisce perpendicolarmente la lamina.

Utilizzando lo stesso sistema “serio” vedremo, tra poco, cosa succede alla luce che penetra nel vetro e finisce nel rivelatore al di sotto della lamina. Coloro che sono riusciti ad affrontare la parte appena conclusasi senza grossi problemi, possono anche cercare di descrivere, da soli, il passaggio attraverso la lamina. Questa sarà sempre divisa in sei straterelli, ma sarà ancora necessario considerare traiettorie partite in tempi diversi?

Provateci… è più semplice di quanto non sembri, basandosi sempre sullo scattering, dato che ormai siamo abbastanza “grandi” da scrivere parole compiute nel nuovo alfabeto. Anche se -forse- non li analizzeremo in dettaglio, si può intuire come  i  fenomeni di scattering siano tutti riconducibili a una sola parola del mondo di Alice…

Abbiamo visto che vi sono molte strade per giungere al rivelatore R₁, attraverso la doppia riflessione (che sappiamo essere stata una semplificazione indolore), dato che ogni punto della lamina contribuisce alla probabilità finale attraverso l’umile lavoro degli elettroni del vetro, capaci di assorbire e di riemettere fotoni nella direzione che ci interessa. Sono dei veri e propri “fucili mitragliatori” che raccolgono proiettili e li sparano verso il bersaglio.

Zone diverse del vetro, però, vogliono dire percorsi più o meno lunghi e quindi istanti di partenza, dalla sorgente, diversi. Ormai sappiamo che non esiste il famoso cronometro, ma che la direzione dell’ampiezza si origina fin dall’inizio a seconda dell’ora segnata da un unico orologio, al momento della partenza della luce monocromatica. Essa viene ristretta e rivoltata solo quando gli elettroni fanno il loro lavoro, ossia quando applicano la terza lettera dell’alfabeto: l’interazione o accoppiamento.

Un fotone che non … riflette

Pensiamo, allora, alle traiettorie del nostro fotone che voglia  attraversare tutta la lamina e arrivare in R₂ (perché lo faccia lui e non i suoi fratelli riflessi resta, ovviamente, un mistero). Disegniamo la Fig. 66. Come già fatto precedentemente, consideriamo solo percorsi rettilinei. Il modo migliore per arrivare in R₂ è quello di non incontrare nessun elettrone, ossia non subire scattering. E’ sicuramente la via più diretta e più probabile, dato che non vi sono accorciamenti o rotazioni. La sua ampiezza è decisamente grande, praticamente identica a quella iniziale (a parte l’affievolimento dovuto alla distanza da percorrere, che NON dipende dal vetro). Tuttavia questa stessa traiettoria è irta di ostacoli: gli elettroni del vetro.

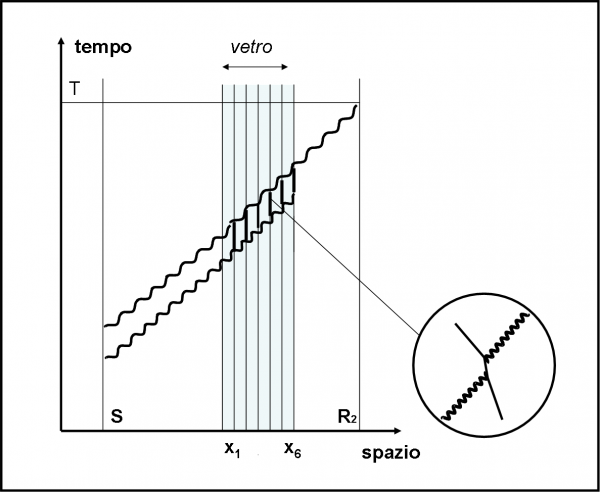
Altri fotoni (o, meglio, altri percorsi alternativi) possono dar luogo a scattering. In prima approssimazione, prendiamo in considerazione le ampiezze che derivano da uno scattering avvenuto all’interno di uno dei sei “straterelli” del vetro. Esse sono decisamente più corte di quella “diretta” e, inoltre, sono ruotate di 90° (come nel caso della riflessione… siamo o non siamo nel vetro?). Tuttavia, ognuna subisce la stessa identica azione e quindi sono tutte uguali tra loro. Cosa dire della loro direzione? Sappiamo che dipende dal momento della partenza dalla sorgente S. Ma, questa volta, tutte le varie alternative da tenere in conto avvengono sullo stesso percorso spazio-temporale, dovendo arrivare tutte in R₂ al tempo T (qualcuna esegue lo scattering prima, altre dopo, ma alla fine il percorso è uguale, ossia attraversa tutta la lamina). La luce deve quindi essere inviata da S nello stesso istante. Quella “diretta” appare inviata dopo, ma in realtà lo scattering potrebbe essere immediato. In ogni modo,  c’interessa poco, dato che la differenza di direzione è compresa nella rotazione di 90° (come già considerato nella riflessione).

In conclusione, abbiamo una freccia molto lunga (praticamente unitaria) a cui si devono sommare sei freccette uguali, ruotate tutte di 90° e quindi situate lungo la stessa direzione, come rappresentato in Fig. 67.

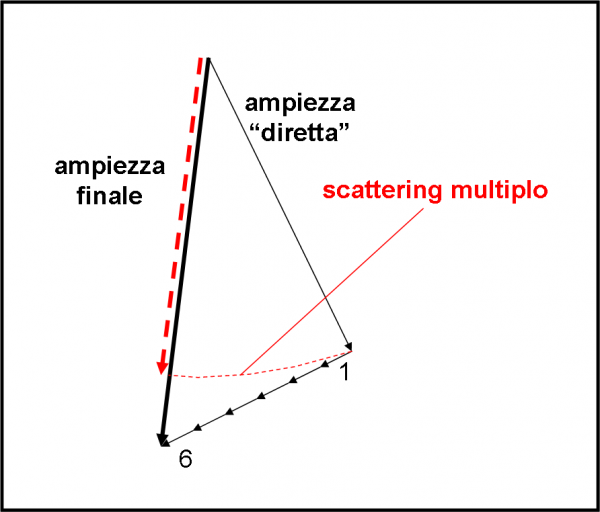
A prima vista sembrerebbe che l’ampiezza finale sia più lunga di quella della via diretta. In realtà non è vero, se si considerano scattering multipli (in pratica, quello che avevamo fatto considerando riflessioni multiple all’interno del vetro). Alla fine si ottiene una freccia finale che è, al massimo, uguale, come lunghezza, a quella della luce diretta. D’altra parte deve essere così se non si vuole concludere che mettere una lamina di vetro davanti alla luce aumenti la probabilità rispetto a un percorso senza alcun ostacolo! Lo scattering multiplo gioca in modo che non si ottenga più luce di quanta se ne invii… e inoltre permette all’ampiezza finale di andare da 0.92 a 1 e, di conseguenza, assecondare la riflessione e ottenere una probabilità finale, data dalla somma “bruta”  dei due eventi separati (riflessione e trasmissione), pari al 100%. La Natura lavora in modo bizzarro, ma non sbaglia un colpo… come la QED ci dimostra!

Il fatto che l’ampiezza finale, dopo la trasmissione attraverso il vetro, ruoti rispetto a quella del passaggio senza scattering (percorso diretto, come se vi fosse solo aria), crea l’impressione che il vetro ritardi il passaggio della luce (ossia la luce impieghi più tempo). In realtà, questo effetto è dovuto alla rotazione e all’accorciamento della freccia a causa dello scattering. Questa capacità di “rallentamento” dovuto alla minore o maggiore inclinazione della freccia finale si chiama indice di rifrazione del materiale. Lo stesso effetto si ottiene, ovviamente, aumentando lo spessore del vetro, dato che si sommano più freccette e la direzione finale si piega di più. Questo è il vero fenomeno su cui si basa una lente, che utilizza uno spessore variabile. In parole semplici, dato che la freccia finale ha una certa inclinazione rispetto a quella senza scattering (ossia quella prima dell'entrata nel vetro) si conclude che essa deve essere partita a un tempo diverso rispetto a quello dell'ampiezza senza scattering. Tempo diverso vuol dire più tempo per raggiungere il rivelatore... e il gioco è fatto: la luce sembra viaggiare più lentamente.

Quanto detto vale per materiali trasparenti. Se il materiale è più “opaco”, la direzione delle freccette da sommare a quella principale fa un angolo minore di 90° e quindi l’ampiezza finale si riduce rispetto a quella diretta. Non solo ruota, ma si accorcia di molto. Questo vuol solo dire che un materiale opaco ha una minore probabilità di essere attraversato dalla luce. Vediamo la situazione in Fig. 68.

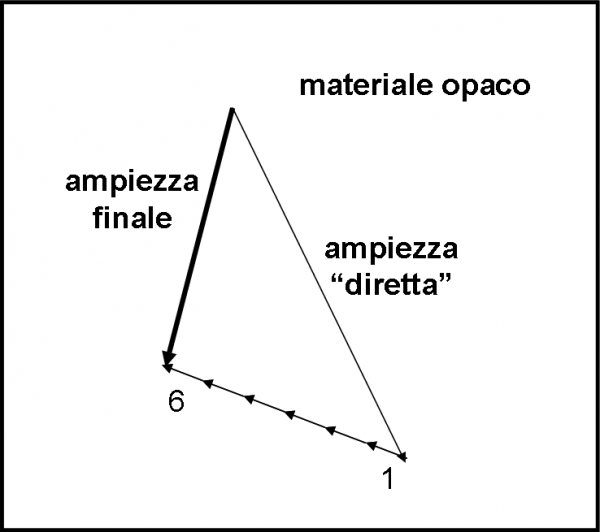
Uno più uno uguale a quattro

Sembra impossibile che tutti i fenomeni di interazione tra luce e materia possano essere descritti attraverso tre sole lettere di un alfabeto. Se entrassimo a fondo nella matematica che c’è dietro riusciremmo a verificarlo direttamente. Ma questa impresa va oltre le nostre possibilità. Limitiamoci a pochi altri fenomeni e poi abbandoniamo con un po’ di nostalgia la QED.

Torniamo al ben noto fenomeno dell’interferenza, che ormai conosciamo come le nostre tasche. Affrontiamolo nello spazio-tempo. Consideriamo il caso più generale: due sorgenti S₁ e S₂ e due ricevitori R₁ e R₂. L’evento da verificare è: un fotone parte da S₁ e uno da S₂. Entrambi devono raggiungere R₁ e R₂. Sappiamo che esistono due vie perché l’evento accada. Le traiettorie S₁R₁ e S₂R₂, ma anche la S₁R₂ e la S₂R₁ (Fig. 69) Le ampiezze associate ad esse sono: P(S₁,R₁), P(S₂,R₂), P(S₁,R₂) e P(S₂,R₁). Esse vanno moltiplicate a coppie, dato che solo così si ha l’ampiezza finale per ogni alternativa. Abbiamo le frecce P(S₁,R₁) x P(S₂,R₂) e P(S₁,R₂) x P(S₂,R₁). I due risultati vanno sommati vettorialmente per ottenere l’ampiezza finale. Una vera banalità per noi. Agendo così nasce il fenomeno dell’interferenza, dato che, variando le posizioni relative delle sorgenti e/o dei rivelatori, possiamo avere sia la somma che l’annullamento della luce.

Immaginiamo, ora, che i due rivelatori si sovrappongano. Vale comunque il calcolo di prima che porta, però, a due ampiezze uguali attraverso la moltiplicazione, dato che P(S₂,R₁) = P(S₂,R₂)  e P(S₁,R₁) = P(S₁,R₂). Ossia, P(S₁,R₁) x P(S₂,R₁) = P(S₂,R₁) x P(S₁,R₁). Ne consegue un’ovvia … ovvietà: in R₁= R₂ = R,  entrambe le vie danno la stessa ampiezza (freccia) da sommare.  Lunghezza e direzione sono identiche per costruzione! La somma delle due frecce è uguale a 2 volte l’ampiezza singola e, quindi, dato che la probabilità finale  è il quadrato dell’ampiezza finale, essa è pari a quattro volte quella della singola moltiplicazione. La faccenda è rappresentata in Fig. 70.

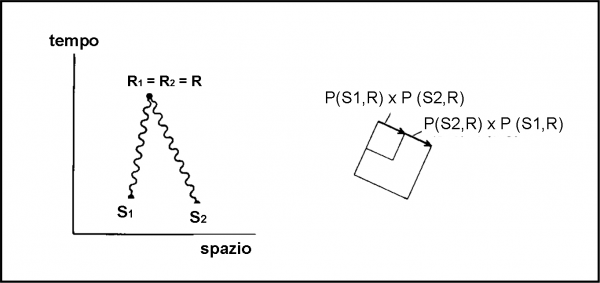
Abbiamo detto qualcosa di interessante? A prima vista sembrerebbe di no. Ma, pensiamoci, un po’ sopra… Se spostassimo le due sorgenti, cosa succederebbe? Una cosa del tutto identica: si otterrebbe, in R, sempre la somma di due frecce identiche e una probabilità quattro volte quella della singola moltiplicazione. L’interferenza non fluttuerebbe più, ma sarebbe sempre positiva. Per farla diventare zero dovrebbe essere nulla la singola freccia, che, però, non lo è sicuramente.

Se aumentassimo il numero di fotoni che escono dalle sorgenti, l’effetto sarebbe sempre più macroscopico. In altre parole, questo risultato vuol dire che i fotoni tendono verso una stessa “condizione” (il rivelatore è una condizione) o -meglio- “stato”. Non possiamo approfondire di più, ma i risultati pratici sono enormi. La probabilità che un atomo emetta un fotone aumenta di molto se alcuni fotoni sono già presenti. Questo fenomeno è stato studiato da Einstein e prende il nome di emissione stimolata. I laser lavorano proprio basandosi su di lei.

O uno o l’altro

Se facessimo la stessa cosa con gli elettroni dovremmo trovare lo stesso risultato. Invece capita proprio il contrario, dato che bisogna tener conto che essi sono polarizzati (finora non avevamo avuto bisogno di inserire questa caratteristica fondamentale). Si può dire che il loro spin NON può essere zero (ma questa è un’altra storia). In ogni modo, ciò che capita è che le due frecce ottenute dalle due moltiplicazioni, hanno uguale ampiezza e verso opposto (Fig. 71). Ciò vuol dire che l’ampiezza finale è sempre ZERO. In parole povere, gli elettroni, a differenza dei fotoni, non amano andare nello stesso luogo! E questo, in fondo, lo sappiamo bene…

Più tecnicamente, si conclude che due elettroni con lo stesso spin non possono trovarsi ambedue nella stessa posizione. Questo risultato prende il nome di principio di esclusione. Penso che questo nome non suoni tanto astruso … Da questo principio seguono moltissime delle proprietà chimiche dell’atomo. Tutto si basa solo e soltanto sullo scambio di fotoni tra protoni ed elettroni e sulla loro impossibilità di convivere con i fratelli. Se gli elettroni non fossero polarizzati si ammucchierebbero tutti attorno al loro nucleo atomico e non potrebbero essere catturati facilmente da altri atomi. Insomma: le reazioni chimiche sarebbero molto, molto difficili! Un giorno, magari, ne parleremo.

Un inseguimento perfetto

Senza entrare nei particolari tecnici, facciamo un esempio di come la QED abbia aiutato nel calcolare teoricamente un “numero” estremamente importante nel contesto della fisica delle particelle elementari. Il grande Dirac riuscì a calcolare il momento magnetico di un elettrone, ossia la risposta dell’elettrone a un campo magnetico esterno. Il valore venne determinato attraverso i calcoli e risultò essere uguale semplicemente a 1, in certe unità di misura. In seguito si ci accorse, attraverso gli esperimenti, che quel valore non era esatto ed era pari a circa 1.00118. Cercando di miglioralo attraverso considerazioni teoriche la faccenda degenerò, dato che il numero tendeva a infinito, ossia a un’assurdità. Una prima e rozza applicazione della QED ottenne, invece, 1.00116, ben più vicino al valore sperimentale. La strada era quella giusta.

Negli anni ’80 del ventesimo secolo, la QED ottenne un valore di 1.00115965246 (con un errore di 5 unità nell’ultimo decimale) contro un valore sperimentale di 1.00115965221 (con un’incertezza di 4 unità nell’ultima cifra). Un risultato niente male, se pensiamo che stiamo parlando di incertezze equivalenti allo spessore di un capello di una persona di New York, visto da Los Angeles.

Come si è arrivati a questo risultato eccezionale? Facile (si fa per dire): aggiungendo più lettere alla “parola” base dell’interazione elettrone-fotone. Il valore 1 ottenuto da Dirac, si riferisce, infatti, alla traiettoria più semplice, ossia a quella di un elettrone che assorbe un fotone generato dal campo magnetico (Fig. 72).

Complicando leggermente il percorso (ossia introducendo un’altra interazione) si arriva al valore di 0.00116. Qual è questo percorso alternativo? Lo vediamo in Fig. 73. E’ capitata una cosa “assurda”, ma non certo per il mondo di Alice: un fotone virtuale è stato emesso ed è stato riassorbito dallo stesso elettrone. Un gesto di cannibalismo? No, cari amici, le formule della QED lo ammettono e non dobbiamo farci condizionare dal nostro … moralismo.

Intanto, però, gli esperimenti miglioravano il numero, aggiungendo nuovi decimali. Problemi? No di certo per la QED. Bastava aggiungere altri percorsi alternativi come quelli raffigurati in Fig. 74. Nessuna sorpresa, ammettendo perfino, ultimo grafico a destra, che un elettrone e un positrone si creino da un fotone e si distruggano per emettere un nuovo fotone (cerchietto che si chiude su se stesso).

Il valore sperimentale migliorava ancora? E, allora, via con qualche ulteriore “accoppiamento”, come mostrato nella Fig. 75, che rappresenta solo tre di una serie di 70 “combinazioni”: il valore teorico rimane incollato a quello sperimentale. Fantastico. Malgrado la Natura tenti di essere sempre più imprevedibile, la QED non si fa impressionare.

Non crediamo, però, che sia stato facile aumentare gli accoppiamenti e calcolare la quantità da aggiungere, proveniente da un numero sempre crescente di percorsi alternativi. Ogni miglioramento ha avuto bisogno di periodi di tempo molto lunghi, che l’avvento dei supercomputer ha decisamente sveltito, fino a portare alla precisione odierna… (se non sbaglio, dovremmo essere a 1.01159652188 sperimentale contro 1.01159652140 teorico). Sembra un bel piccolo miglioramento, ma più si va nel piccolo e più le combinazioni aumentano e di conseguenza i calcoli relativi… In qualche modo si è spaccato un capello in dieci!

Conclusioni

C’è poco da dire. La QED sembra uniformare tutti i fenomeni della fisica (funziona anche con altre particelle e non solo con i fotoni e gli elettroni). Quello che stupisce è la semplicità dell’alfabeto e la continua ripetizione di azioni sempre uguali tra loro: moltiplicazioni e somme di ampiezze. Eppure tutto (o quasi) torna benissimo. Feynman non  è stato l’inventore della QED, ma, a parte il contributo fondamentale che gli è valso il Nobel, solo lui è riuscito a renderla simile a una semplice e fantastica avventura. Non ci resta che applaudirlo!!!

Una bella fatica, ma penso ne sia valsa la pena…