Categorie: Fisica classica Meccanica quantistica Stelle
Tags: atomo corpo nero elettroni energia fotoni quanti spettro di assorbimento spettro di emissione spettroscopia
Scritto da: Vincenzo Zappalà
Commenti:17
Dall'atomo alle stelle e viceversa: struttura atomica, righe spettrali ed elettroni saltellanti ***
Questo articolo è stato inserito nella sezione d'archivio "Dall'atomo alle galassie".
Lo scopo di questo lungo articolo è essenzialmente uno: CAPIRE COS'E' LA MATERIA E COME SI ORGANIZZA. Un problema ancora aperto anche se il suo studio è iniziato praticamente con l'uomo. La cosa migliore da fare è affrontare l'argomento dai due capi opposti, dall'infinitamente piccolo e dall'infinitamente grande (rispetto alla nostra realtà quotidiana). Da un lato la materia deve essere descritta studiando la sua essenza più profonda, i mattoncini con cui è costruita, ma, dall'altro, solo le manifestazioni più grandi della Natura possono farci capire come funzionano realmente le cose. La materia non conosce limiti che la possano dividere in zone o intervalli. Se vengono utilizzati è solo per motivi di comodità descrittiva.
Usando un fantascientifico strumento che possa condurci dal più piccolo al più grande, ci si renderebbe conto che esistono leggi e regole diverse a seconda dei fenomeni da studiare e degli attori coinvolti, ma che tutto porta a un'unica rappresentazione generale, in cui le dimensioni perdono del tutto le caratteristiche che noi cerchiamo di imporle. In parole molto semplici: per capire come funzionano i giganti materiali del Cosmo (le stelle) è necessario studiare le creature più piccole della materia (le particelle); tuttavia, per capire come funzionano e come interagiscono le particelle è necessario studiare i fenomeni giganteschi delle stelle. Un abbraccio totale e strettissimo che trova il suo campo di gioco nello spaziotempo, il perfetto teatro perchè gli attori, indipendentemente dalle loro dimensioni, possano dare il meglio di sé.
Per cercare di perseguire questo scopo, utilizzeremo una strategia operativa un po' saltellante. Inizieremo con la ricerca della struttura dell'infinitamente piccolo. Quando giungeremo vicini a una soluzione accettabile, che si avvicini sempre più alla realtà dei fatti, faremo un salto enorme e andremo a studiare le stelle fino a che i loro problemi più profondi potranno essere risolti solo legandole strettamente alle caratteristiche della struttura delle particelle più piccole che le compongono. L'ultima parte del percorso sarà in comune e aprirà scenari ben più ampi verso le teorie e le osservazioni più moderne.
Non potremo certo dire di conoscere la materia e le sue manifestazioni, ma saremo arrivati a un punto sufficiente per comprendere, almeno, con chi stiamo giocando!
La materia è dappertutto
Immaginiamo di essere un po’ come il principe che abbiamo usato spesso come entità al di fuori del tempo e dello spazio. Non abbiamo sensi che ci permettano di ricevere informazioni dall’esterno e/o di avere qualsiasi tipo di interazione con ciò che esiste (e se esiste). Abbiamo, però, una mente pensante e riflessiva. Improvvisamente, veniamo trasportati nel mondo reale e ci vengono regalati i cinque sensi. Per la prima volta vediamo che esistono tante cose, a volte uguali a volte estremamente diverse; a volte piccole e a volte grandissime. Molte si muovono e altre stanno ferme (apparentemente). Alcune non si possono rompere, altre si spezzano con grande facilità. Alcune ci sbarrano il cammino e altre si intuiscono soltanto. Un esempio? la vela di una nave che è spinta da un qualcosa che non si riesce a vedere o un otre che si gonfia se si soffia al suo interno solo il nostro invisibile respiro.
Domanda: “Solo e soltanto con i nostri limitati sensi saremmo capaci di descrivere la Natura?”. Devo dire la verità, sull’uomo di oggi sarei molto pessimista. Sbaglierò, ma se non trovasse la “pappa pronta”, preparata da anni costellati di menti illuminate, l’uomo moderno saprebbe usare la tecnologia come potrebbe fare una scimmia, ma ben difficilmente capirebbe o -soprattutto- cercherebbe o vorrebbe capire ciò che lo circonda (presenti esclusi, ovviamente!).
La Natura resterebbe un mistero da accettare e da sfruttare: niente di più e niente di meno. Eppure, vi erano personaggi come noi, senza, però, alcuna “pappa pronta”, che già parecchi secoli prima di Cristo erano riusciti, se non a risolvere questo mistero, almeno a porselo e a trovare strade teoriche per descriverlo. Non voglio certo addentrami nelle meraviglie deduttive degli antichi popoli e soprattutto dei greci (perderemmo su tutti i fronti e non avrei pagine a disposizione), ma solo riferirmi a come alcuni pensatori abbiano rappresentato l’avventura forse più grande ed elaborata della storia del pensiero umano: la struttura della materia.
E’ un’avventura che unisce l’infinitamente piccolo con l’infinitamente grande e già questo dato di fatto illustra molto bene la sua complessità e vastità. Essa è nata in tempi in cui non esistevano microscopi, laboratori del CERN, telescopi per scoprire cos’erano quelle migliaia di luci che splendevano nel cielo. Spesso gli studiosi (non solo curiosi) avevano solo un bastone, un dromedario e tanta … intelligenza. Infatti, ciò che sicuramente esisteva era la mente, quella attiva, sempre pronta a recepire e a elaborare.
Uno dei maggiori problemi “mentali” del secolo scorso è stato il passaggio dalla fisica classica alla relatività di Einstein e alla sua pacifica battaglia con la meccanica quantistica. Ancora oggi, però, le scuole di livello medio-alto tengono certi concetti ben lontani dalle conoscenze dei giovani, quasi fossero ancora “eretici” (la scusa della difficoltà è un alibi che non ha alcun senso) e potessero trascinare docente e discepolo in un qualche terribile tribunale della Santa Inquisizione. Un po’ come quando io frequentavo le superiori negli anni ’50-60 e la storia d’Italia finiva, per bene che andasse, con qualche cenno sulla prima guerra mondiale. Il resto era ancora top secret!
Quando si parla di meccanica quantistica con le persone comuni sembra di parlare di un qualcosa al di fuori delle possibilità umane. Spesso si registrano sorrisi, scrollate di spalle, mani che si tappano le orecchie e frasi del tipo. “No, non è per me!”. E siamo nel ventunesimo secolo dopo Cristo. Ben pochi immaginano che la meccanica quantistica era già nata, da un punto di vista concettuale, nel V secolo avanti Cristo (almeno, per quanto ne sappiamo, ma potrebbe anche essere prima). Ha dovuto aspettare secoli e secoli, così come lo studio dell’Universo, prima di poter tornare libera nelle menti dell’uomo (prendiamo questo periodo di buio scientifico come un dato di fatto e non commentiamolo).
Il duello matematica-fisica, ovvero spirito-materia
Vi ricordate il paradosso di Zenone, quello che dimostra matematicamente che Achille non potrebbe mai vincere una gara di corsa contro la tartaruga? L’abbiamo descritto come un esempio classico della differenza sostanziale che esiste tra matematica e fisica. La prima accetta tranquillamente il concetto di zero e di infinito, non teme il pensiero astratto; la seconda è costretta a muoversi a scatti, per piccoli che siano e si pone limiti invalicabili, “materiali”.
Non è forse un concetto molto simile alla meccanica quantistica? Il problema di una Natura continua, contrapposta a una Natura formata da “pacchetti” infinitesimi, fatta di pixel invisibili (tanto per far contenti anche coloro che sanno tutto su come fotografare una galassia, ma che non hanno la minima idea di cosa sia la costante di Planck) è un problema che persone come Democrito ed Epicuro avevano già espresso e sviluppato ben prima che la scienza di tipo “religioso”, spirituale, astratto, dogmatico e inconfutabile, bloccasse, per paura, le menti più libere, per tanti secoli a venire.
L’atomo, l’indivisibile
Due nomi vanno ricordati sopra tutti, anche se le teorie e i nomi spesso non vanno d’accordo, dato che i pochi documenti sono frammentari e difficili da riferire veramente a persone singole o a gruppi … di ricerca: Leucippo e il suo allievo Democrito (ben più famoso). I pensatori greci si erano posti il problema della materia e vi erano due scuole di pensiero, che potremmo dire di tipo matematico e fisico. La prima considerava la materia composta da parti divisibili all’infinito, un qualcosa di continuo, tale che per un intervallo piccolo a piacere esistesse sempre un pezzetto di materia più piccola. Una visione alla Zenone, insomma… La seconda invece assumeva che la materia fosse composta da parti indivisibili, ossia di “atomi” (in greco significa proprio “non divisibile”).
Un problema essenzialmente filosofico, dato che non vi era alcuna possibilità di eseguire esperimenti, ma sicuramente una delle più grandi conquiste scientifiche della mente umana. L’idea stessa di pensare a come sia strutturata la materia andando verso l’infinitamente piccolo è una conquista di livello eccezionale. Leucippo e Democrito sono i veri paladini della visione materialistica della Natura.
Da quanto scrive Democrito, sembra che Leucippo avesse diviso il Cosmo in due parti essenziali: l’essere e il non essere. L’essere è la materia, il “pieno”; il non essere è il “vuoto” (ma quello “vero” non l’aria che si respira). Le interazioni tra pieno e vuoto portano a tutte le azioni, ai movimenti e alle forme della Natura. L’essere, cioè il pieno, è formato da un numero infinito di piccolissime strutture indivisibili, di dimensioni diverse, che muovendosi nel vuoto danno a luogo alla molteplicità delle cose tangibili e visibili. Il moto totale è una delle caratteristiche essenziali della meccanica quantistica e la fa scontrare con la relatività generale...
Democrito va ancora avanti e scrive un trattato il cui titolo è già una meraviglia di modernità: “Il piccolo ordinamento dell’Universo”. Già allora era riuscito a legare in modo strettissimo l’infinitamente piccolo con l’infinitamente grande. Un concetto che dire rivoluzionario è dir poco. Il suo trattato approfondisce i concetti di Leucippo. Gli atomi hanno due proprietà: la forma e la dimensione. Unendosi in ordine e modo differenti, danno origine ai diversi composti materiali. Questi gruppi o ammassi atomici producono sensazioni e percezioni se interagiscono con i nostri sensi. Noi vediamo qualcosa quando un gruppo di atomi parte dall’oggetto e colpisce il nostro occhio (i fotoni, in fondo, fanno proprio così...).
Essenziale è, comunque, il loro movimento. Gli atomi si muovono per effetto di forze interne. Inoltre, il movimento determina la “massa” degli atomi, in quanto quest’ultima dipende dalla velocità che gli atomi hanno acquistato attraverso gli urti reciproci (massa relativistica?). Lo stesso moto e le interazioni susseguenti danno origine ai corpi materiali.
Sintetizzando: gli atomi sono di per sé immutabili e la mutevolezza della Natura è dovuta solo alle loro aggregazioni e separazioni causate dal movimento. Le cose nascono e muoiono senza alcuno scopo finale, secondo processi puramente meccanici, dovuti al movimento degli atomi in tutte le direzioni. Beh… stiamo parlando di Democrito e non di meccanica quantistica.
L’apparente ingenuità della visione scompare se si riflette più a fondo. Vi è già presente un movimento continuo delle particelle. L’interazione tra di esse dà luogo alla struttura delle cose, alla sua variazione, e alla sua percezione. Vi è persino una massa che dipende dalla velocità… Le uniche particelle per Democrito sono gli atomi, ma se si scende ancora di un gradino, non è difficile intravedere già gli elettroni, i fotoni, le particelle e le teorie più moderne. Mi chiedo: “Se Democrito fosse portato ai nostri giorni (un po’ come il principe) o -forse ancora meglio- all’epoca dei grandi fisici del secolo scorso, dopo un ovvio momento di sbandamento e acclimatamento, avrebbe grandi difficoltà a entrare nelle problematiche dei modelli atomici di Bohr e addirittura quantistici?". Qualcosa mi dice che si troverebbe a suo agio e anche abbastanza in fretta.
Il principio d’inerzia e della conservazione dell’energia
Senza volare troppo in alto, si può comunque intravedere qualche principio fondamentale della fisica: egli dice, infatti: “Nulla è creato dal nulla e nemmeno si distrugge nel nulla”. Non assomiglia in tutto e per tutto alla legge di conservazione dell’energia? Inoltre dice: “Il pieno, quando si trova nel vuoto, continua nel suo movimento eterno, del quale non si deve chiedere ragione proprio perché esso è primitivo ed è sempre avvenuto”. E’ o non è il principio d’inerzia?
Oltretutto, questa teoria è frutto solo e soltanto del pensiero, senza alcun supporto proveniente da esperimenti del tutto impossibili a quei tempi. Non ci resta che toglierci il cappello e andare avanti…
La mela di Epicuro
Epicuro prosegue il lavoro di Democrito con piccole variazioni, riguardanti soprattutto il numero infinito di forme e di atomi. Per lui il numero deve essere per forza finito. Inoltre, inserisce, come ulteriore proprietà fondamentale, il “peso” dell’atomo. In tal modo dà una spiegazione al moto degli atomi. Essi “cadono”, per effetto del loro peso, dall’alto verso il basso, in linea retta proprio come la pioggia, tutti alla medesima velocità (qualsiasi riferimento alla mela di Newton NON è del tutto casuale!). Come possono allora scontrarsi e dare origine alla materia? Epicuro se la cava attraverso la “deviazione”, un fenomeno del tutto “casuale”. Questa visione apparentemente debole e priva di qualsiasi logica, ha fatto sorgere molte opposizioni alla teoria di Epicuro.
E’ estremamente interessante citare ciò che disse Cicerone, come presa in giro, e che oggi suona in modo ben diverso: “Come fanno gli atomi a decidere chi di loro deve deviare e chi no? Tirano a sorte?”. Anche qui il famoso Dio che gioca a dadi sembra essere anticipato di secoli e secoli e, analogamente, la conclusione di Feynman: “Nessuno può spiegare perché un fotone si rifletta nel vetro e un altro no”. Epicuro sceglie questa strada “azzardata” per una ragione ben precisa: accentuare proprio la casualità dei fenomeni e della struttura dell’Universo.
Sbaglio o sarebbe molto istruttivo tornare a leggere ciò che gli antichi hanno scritto, senza partire da visioni prevenute imposte dagli alibi di una tecnologia spinta verso eccessi mostruosi? Le capacità mentali e razionali non dipendono dalla tecnologia. Se mai, ma non sempre, è vero il contrario.
La materia deve essere impura: il lungo buio della mente.
Purtroppo questa visione del mondo piuttosto “atea” trova un validissimo oppositore in Aristotele, che divide il mondo in due parti distinte: quella celeste e quella terrestre. La prima è incorruttibile e segue regole perfette di una geometria immobile e invariabile. La seconda è corruttibile e imperfetta, formata da un continuo miscuglio di elementi. La visione atomistica diventa insostenibile e perseguibile come blasfema.
La Chiesa accetta in pieno l’idea aristotelica e vede nella teoria atomica un pericolosissimo concetto materialistico. La Natura non può certo basarsi su interazioni casuali di particelle. Chi osa proporle non può che essere considerato un eretico. Una situazione analoga a quella della visione geocentrica dell’Universo. Tuttavia, mentre quest’ultima deve aspettare il XVI secolo per essere finalmente messa in discussione, per la teoria atomica si deve attendere Dalton e il XVIII secolo.
La teoria di Democrito e l’elaborazione di Epicuro, oltre ad aver introdotto l’elemento base della materia, rappresentano il primo passo fondamentale verso la chimica. Purtroppo l’opposizione di Aristotele e la susseguente visione dogmatica e assolutista della Chiesa hanno bloccato il processo conoscitivo: le trasformazioni della materia sono diventate patrimonio dell’alchimia. Sarebbe affascinante seguirne l’evoluzione, in cui, di tanto in tanto, si aprono spiragli scientificamente validi che però ricadono velocemente nel calderone della stregoneria. Non possono, quindi, che rimanere episodi isolati, senza scambi di pensiero e di idee, sempre ai margini della dannazione.
La chimica fuori legge
Tuttavia, non si possono certo negare i risultati importantissimi ottenuti da una pratica del tutto empirica, contaminata da mistificatori e ciarlatani, ma spesso costellata di successi. Le scoperte di questa pseudo-scienza hanno dato un contributo essenziale, anche se non cercato, al progresso della chimica, ossia alla vera scienza. Il ruolo dell’alchimia può essere sintetizzato benissimo nella favola citata dal filosofo inglese Francesco Bacone, vissuto tra il XVI e XVII secolo: “Un uomo svela ai figli di aver nascosto dell’oro in un luogo imprecisato della sua vigna. I figli si lanciano a cercarlo, scavando fra le piante senza tuttavia trovare nulla. Lavorano, però, il terreno così bene da ottenere un’abbondante vendemmia!”.
E’, probabilmente, ancora una volta Galileo a segnare un punto di non ritorno, attraverso i suoi esperimenti sulla caduta dei gravi. Non tanto per il concetto in sé, che dimostra come la velocità degli oggetti sia indipendente dalla massa, ma per il fatto di avere confermato, senza ombra di dubbio, che anche Aristotele poteva sbagliare! Tuttavia, bisogna aspettare ancora parecchio.
Il primo modello di atomo su base scientifica, ossia attraverso sperimentazioni, si deve a John Dalton che lo presenta nei primi anni dell’800, basandosi su due leggi fondamentali della chimica enunciate da Lavoisier e Proust e su una che deduce egli stesso. Vale la pena entrare nei dettagli della geniale intuizione di Dalton. Teniamo presente che non è tanto la struttura dell’atomo che interessa allo scienziato inglese, ma come esso si comporti nelle reazioni chimiche.
L’inizio di una svolta decisiva nella storia dell’atomo e la nascita della chimica come vera scienza si può ricondurre alla teoria del flogisto (dal greco bruciare, infiammare) che va per la maggiore nel XVII secolo. In base a essa, tutto ciò che brucia libera, nell’aria, una sostanza, il flogisto, appunto. Le sostanze combustibili, sono ricche di flogisto e il processo di combustione cede questo strano elemento all’aria, la quale lo può trasferire ad altri corpi che quindi diventavano a loro volta combustibili. Ciò che rimane, dopo la combustione, ha perso il flogisto e quindi non brucia più. La legna, ad esempio, contiene flogisto, ma non la cenere. Il peso nettamente differente lo dimostra.
Tralascio l’esistenza di un flogisto con peso negativo nei casi di ossidazione. Insomma, una bella teoria chimica che fa riferimento ai pesi delle sostanze implicate, anche se si mettono le cose a posto con l’introduzione di una sostanza quasi magica, legata all’alchimia. Tuttavia, la necessità di formulare questa teoria si basa su un dato di fatto “scientifico” sperimentale: il peso di una sostanza prima della combustione è maggiore di quello della sostanza che rimane dopo la combustione. La soluzione è un po’ da “stregoni”, ma il problema è stato evidenziato!
Un "lego" microscopico
La vera soluzione è trovata dal grande chimico Lavoisier nel 1783, che inserisce nella trasformazione il peso dell’aria ed enuncia la prima e fondamentale legge della chimica ponderale (ossia riferita al peso delle sostanze):
(1) In una qualsiasi reazione chimica la somma dei pesi delle sostanze che reagiscono è uguale alla somma dei pesi delle sostanze che in essa si formano.
Detta, in altre parole, acquista una significato ancora maggiore: nulla si crea e nulla si distrugge, ma tutto si trasforma.
Una mente veramente fuori dal comune, anzi… potremmo dire una “testa” eccezionale. Peccato che siamo ai tempi della rivoluzione francese e la nuova repubblica non ha bisogno di scienziati (questa frase non suona molto nuova…) e Lavoisier viene ghigliottinato nel 1794. Il grande matematico italiano Lagrange dice, a riguardo: “Pochi istanti sono bastati a far cadere una testa e non basterà un secolo a crearne una uguale”. Oggi, non si tagliano più le teste, ma si obbligano -spesso- ad andare all’estero. Va beh… torniamo a noi e alla seconda legge ponderale, dovuta a Proust.
Dopo Lavoisier nulla può essere come prima e il suo compatriota Proust dimostra sperimentalmente che un composto ha sempre la stessa composizione, ossia le stesse proporzioni degli elementi che lo costituiscono, indipendentemente dalle condizioni in cui esso è stato preparato. Due elementi reagiscono secondo ben determinati rapporti di “peso”, e un eventuale eccesso di uno dei due non partecipa alla reazione. L’alchimia sembra ormai una pseudo-scienza preistorica…
Questa sua conclusione lo porta, dopo pochi anni, tra il 1799 e il 1801 alla seconda legge ponderale della chimica:
(2) In qualunque composto, il rapporto tra i pesi degli elementi costituenti è definito e costante.
Molto bella una sua riflessione a riguardo: “Un composto è un oggetto che la Natura non crea altrimenti che con la bilancia in mano". Per inciso, è bene ricordare che Proust è decisamente più lungimirante del suo sfortunato collega e si rifugia in Spagna dopo lo scoppio della rivoluzione francese, salvando la propria ... testa, un altro patrimonio dell'umanità.
Le due leggi non possono non avere implicazioni profonde sulla struttura della materia. Non tanto per la descrizione dell’atomo, quanto per i suoi modi di comportarsi. John Dalton fa “uno più uno uguale a due” e giunge a una conclusione ancora più elaborata che rappresenta la terza legge ponderale della chimica, enunciata nel 1803:
(3) Le quantità (pesi) di un elemento che si combinano con una stessa quantità (peso) di un altro, nei loro vari composti, stanno tra loro secondo rapporti semplici, espressi cioè da numeri interi e piccoli.
Spieghiamo “matematicamente” come questa legge, insieme alle prime due, porti Dalton a una vera e propria teoria atomica globale. Immaginiamo che un atomo dell'elemento X, di peso mx, si combini con un atomo dell'elemento Y, di peso mY, per formare il composto XY. Il peso (oggi diremmo massa) totale MXY del composto è data da un ugual numero n di atomi di X, con peso mx, e di atomi di Y, con peso mY, ossia:
MXY = n mx + n mY = n (mx + my) (legge di Lavoisier)
Il rapporto tra il peso MX di X e quello MY di Y è dato da:
MX/MY = n mx/n mY = mx/mY
ed è quindi uguale al rapporto (definito e costante) tra il peso di un singolo atomo di X e quello di un singolo atomo di Y. (Legge di Proust)
Nel caso di più composti formati dagli stessi elementi, essendo gli atomi indivisibili, questi si possono combinare solo secondo numeri interi: ad esempio 1 di X e 1 di Y, 1 di X e 2 di Y, 1 di X e 3 di Y, 2 di X e 3 di Y. In questo modo i rapporti tra le quantità di uno stesso elemento, che nei vari composti si combinano con una quantità fissa dell'altro, sono sempre dati da numeri interi e piccoli, come prevede proprio la legge di Dalton.
Facciamo qualche semplice esempio. Consideriamo l’ossigeno e l’idrogeno. Essi possono formare l’acqua che porta a un rapporto dei pesi tra idrogeno e ossigeno uguale a 1/8. Nel caso dell’acqua ossigenata il rapporto diventa 1/16. Il rapporto tra 8 e 16 è 1/2, proprio un rapporto di numeri interi piccoli (sembra quasi di essere tornati nel mondo straordinario delle risonanze di moto medio …).
Lo stesso capita per i composti ossigeno e carbonio. Nell’ossido di carbonio si ha un rapporto 12/16 tra carbonio e ossigeno. Nell’anidride carbonica, il rapporto diventa 12/32. Semplificando abbiamo i rapporti 3/4 e 3/8. ossia 3 g di carbonio hanno bisogno di 4 g e di 8 g di ossigeno. In altre parole la quantità di ossigeno è data, nei due composti, dal rapporto 4/8 ossia 1/2.
Ancora più indicativo è il caso dell’ossigeno e dell’azoto: Abbiamo cinque composti (protossido d’azoto, ossido d’azoto, anidride nitrosa, biossido d’azoto, anidride nitrica), i quali danno luogo a rapporti tra azoto e ossigeno di 7/4, 7/8, 7/12, 7/16, 7/20 (rispettivamente) . Ciò comporta che a parità di quantità di azoto (7) sono necessarie quantità di 4, 8, 12, 16, 20 di ossigeno, numeri che stanno tra loro nei rapporti 1/2, 1/3, 1/4, 1/5. Scusate se mi sono dilungato un poco, ma dire meraviglioso è dir poco. Non sentite già aria di pacchetti di massa e, quindi, di energia?
Purtroppo, Dalton fa un po’ di confusione tra atomo e molecola (concetto introdotto solo da Avogadro), dando all’acqua, ad esempio, la formula OH. Ma questi sono errori veniali che non toccano la validità della sua legge. L’errore è dovuto semplicemente all’ipotesi che i composti si producano quantitativamente nel modo più semplice possibile e che gli elementi puri siano formati da singoli atomi.
Un atomo molto chimico e poco fisico
La sua teoria atomica può essere sintetizzata attraverso 5 enunciati:
1) la materia è fatta da particelle microscopiche indivisibili e indistruttibili chiamate atomi
2) tutti gli atomi di un elemento sono uguali tra loro e hanno lo stesso peso
3) dagli atomi di un elemento non è possibile ottenere atomi di un altro elemento
4) gli atomi di un elemento si possono combinare solo con numeri interi di atomi di un altro elemento
5) in una reazione chimica gli atomi di un elemento non possono essere né creati né distrutti e si trasferiscono interi formando nuovi composti.
Oggi sappiamo non solo che gli atomi sono ulteriormente divisibili, ma anche che quelli di uno stesso elemento non sono tutti uguali tra loro (isotopi) e che addirittura alcuni possono trasformarsi in atomi di elementi diversi (elementi radioattivi).
Al di là di varie imprecisioni, il modello di Dalton è affascinante e molto realistico. Resta il fatto, però, che nulla dice sulla struttura dell’atomo che viene considerato una pallina sferica perfettamente omogenea. In un primo tempo le aveva anche associato grandezza diversa, a seconda dell'elemento, ma poi la uniforma, facendo variare solo il peso. Ovviamente, la parola peso va oggi trasformata in massa. Alcuni modelli, che gli sono serviti per descrivere vari composti, sono riportati nella Fig. 1.

Altrettanto interessanti sono i simboli che Dalton dà agli atomi con i relativi pesi atomici (spesso del tutto sbagliati per i motivi detti sopra), come mostra la Fig. 2.

La Fig. 3 mostra invece alcuni composti (tra parentesi i valori corretti).
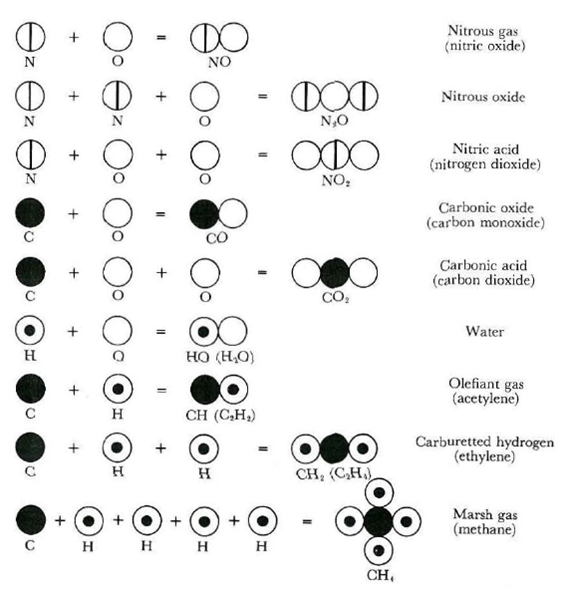
Ricapitolando: Dalton formula la prima teoria atomica basata sulla sperimentazione scientifica che si avvicina moltissimo a ciò che realmente capita nelle reazioni chimiche, ma ipotizza (anche perché non ha alcuna prova sperimentale che possa mettere in dubbio l’ipotesi più semplice), che l’atomo sia un oggetto sferico di dimensioni uguali per tutti gli elementi, ma con peso variabile. Il suo modello apre la strada alla determinazione del peso atomico, dato che il concetto è perfetto, a parte la semplificazione relativa agli elementi “puri” formati da un singolo atomo. Il suo atomo dà un grande contributo alla costruzione della tavola periodica degli elementi di Mendeleev.
Al punto in cui siamo arrivati diventa impossibile seguire con un minimo di attenzione tutte le scoperte scientifiche che si susseguono. Siamo perciò costretti aestrarre e ad analizzare solo quelle che si riferiscono strettamente all’atomo e alla sua struttura.
Il piccolo e sfuggente elettrone
I fenomeni legati all’elettricità (soprattutto l’elettrostatica) sono noti da secoli e secoli e nel 1600 e 1700 s’inventano addirittura giochi da salotto sulle varie applicazioni dell’elettrostatica. Basta dire che già Talete nel 600 a.C. parla delle caratteristiche dell’ambra di attirare a sé oggetti leggeri. Non per niente, in greco antico, ambra ha come nome proprio elektron.
Se dobbiamo scegliere un vero punto di svolta, però, è forse conveniente partire da Franklin, il celebre inventore del parafulmine. Famosi sono i suoi esperimenti con i fulmini, ma soprattutto è fondamentale una sua enunciazione del 1750: “La materia elettrica consiste di particelle estremamente piccole e sfuggenti e può permeare tutta la materia comune, anche la più densa. Le particelle hanno una tale libertà e facilità di movimento da non ricevere nessuna apprezzabile resistenza”.
Si parla ancora di materia elettrica composta da particelle che convive con la materia comune, ma possiamo dire che l’elettrone fa la sua effettiva comparsa teorica. Il concetto viene sviluppato in grande dettaglio, più di un secolo dopo, da Weber, nel 1871, e da Stoney nel 1891, che conia il nome elettrone, in cui la parte finale “one” in inglese significa “uno”, ossia unità. Lo stesso suffisso si applicherà a tutte le particelle future.
Tuttavia, la vera scoperta dell’elettrone avviene per via sperimentale attraverso il tubo catodico di Crookes, un tubo di vetro che contiene un gas molto rarefatto e che ha i due estremi (poli) collegati a un alimentatore in modo che un polo sia negativo (catodo) e uno positivo (anodo). All’interno di questo tubo viene inserita una “croce di Malta” e/o un mulinello a pale in grado di ruotare. Facendo passare corrente, il mulinello inizia il suo movimento rotatorio. Inoltre, la croce produce un’ombra sull’anodo o sulla parete di fondo (spesso, l'anodo è la croce stessa ). Esiste un “fascio” di qualcosa che percorre il tubo ed esso deve avere massa (ossia essere formato da particelle) e deve produrre luminescenza. Al flusso di “particelle” viene dato il nome di raggi catodici.
La Fig. 4 mostra un paio di tubi di Crookes, con tanto di croce di Malta e di mulinello. Va notato che Crookes è interessato all’azione delle scariche elettriche sui gas rarefatti e non riesce a interpretare esattamente ciò che ha scoperto sperimentalmente.
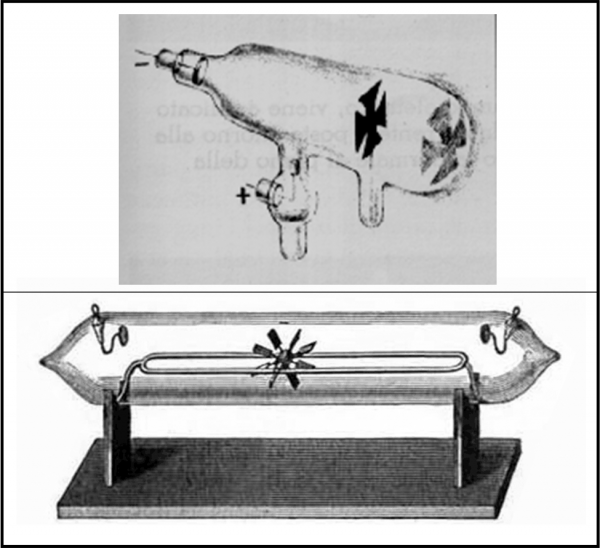
L’esperienza porta facilmente a concludere che i raggi catodici hanno le seguenti caratteristiche:
1) Sono formati da particelle che viaggiano in linea retta, in quanto sono in grado di produrre ombra.
2) Hanno una massa in quanto fanno girare la croce di Malta.
3) Hanno una carica elettrica negativa in quanto sono attratti dall’anodo.
4) Non dipendono né dal tipo di metallo che costituisce il catodo, né dal tipo di gas contenuto nel vetro. Infatti, variandolo, le particelle esistono comunque.
La sintesi dell’esperimento viene compiuta da Thompson, nel 1897, che è in grado di aggiungere due punti ancora più fondamentali:
5) Le particelle possono provenire sia dagli atomi che costituiscono il catodo, sia dal gas contenuto nel tubo.
6) Possiedono tutte lo stesso rapporto carica/massa.
In poche parole: esse sono tutte uguali tra loro ed esistono in tutti gli atomi. L’elettrone ipotizzato da Stoney è stato individuato sperimentalmente!
Il panettone di Thompson
La parte più importante dell’esperimento di Thompson riguarda proprio il punto (6) e viene descritta inserendo un campo magnetico lungo la traiettoria dell’elettrone (Fig. 5). La deviazione subita dalla particella permette di determinare il rapporto tra carica elettrica e massa. Varrebbe la pena andare più a fondo, ma avremmo bisogno di introdurre la forza di Lorentz e il prodotto vettoriale. Ne parleremo in un articolo a sé stante, senza paura del linguaggio della matematica.
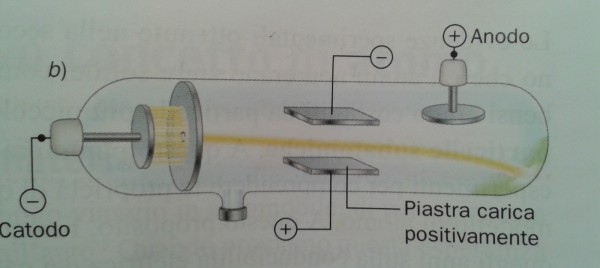
Torniamo al nostro … panettone. In realtà, il modello di atomo proposto da Thompson nel 1904 ricorda proprio un panettone “positivo”, in cui sono inseriti dei canditi “negativi”, gli elettroni. Definiamolo un po’ meglio.
Essendo la materia elettricamente neutra in condizioni normali, ogni atomo deve essere caratterizzato da una carica positiva uguale a quella degli elettroni che contiene. Gli elettroni devono anche essere estremamente più piccoli dell’intero atomo (almeno un migliaio di volte). Ne consegue che la massa dell’atomo, la “pasta” del panettone, ha carica positiva, mentre i canditi, che vi sono inseriti dentro, sono numerosissimi e hanno carica negativa (Fig. 6). Gli elettroni rimangono tranquilli nella pasta fino a quando la materia non viene eccitata, acquistando energia. Essi, allora, cominciano ad agitarsi emettendo onde elettromagnetiche (ossia la luce) o -addirittura- possono abbandonare l’atomo come nel caso dei raggi catodici.
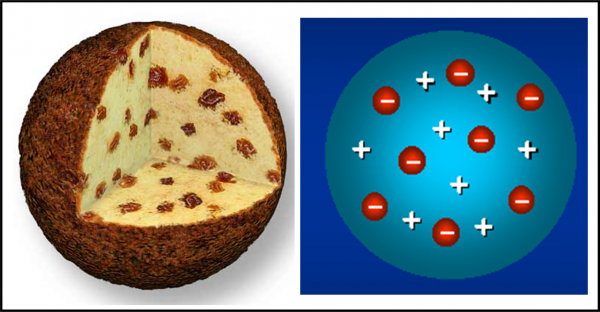
Un modello senz’altro primitivo, ma che già contiene concetti estremamente corretti. Li possiamo notare proprio collegandoli con la QED appena analizzata. Gli elettroni quando si agitano o si spostano (seconda lettera dell’alfabeto di Alice) possono emettere o assorbire fotoni (terza lettera). Siamo, però, in un momento di attività scientifica frenetica e il modello di Thompson può durare ben poco, malgrado sia veramente geniale.
Prima di proseguire, ricordiamo che l’atomo di Thompson spiega l’esistenza degli ioni, ossia particelle con carica positiva e/o negativa. Gli elettroni rappresentano gli ioni negativi, di valore unitario, mentre ciò che resta è uno ione positivo che, nel caso dell’idrogeno (atomo più leggero), viene pure considerato unitario. Nel frattempo, si è anche scoperta la radioattività, ossia la capacità di alcuni atomi di decadere in atomi più leggeri attraverso l’emissione di particelle cariche che possono anche essere positive, come nel caso delle alfa (nuclei di elio). Pur non sapendo ancora cosa sono queste particelle, esse sono comunemente usate per produrre fasci a carica positiva.
Uno scudo atomico
A questo punto arriviamo al fondamentale esperimento di Rutherford del 1909. Lo scopo è, essenzialmente, quello di verificare la validità del modello di Thompson, ma i risultati sono sbalorditivi e non possono che farlo rifiutare.
Lo schema è riportato nella Fig. 7 . Particelle alfa vengono lanciate (la velocità è elevatissima) in modo da attraversare una lamina d’oro sottilissima (lo spessore è stato fatto variare, ma in media è di 0.01 mm). Attraversando gli atomi della sostanza, ossia la pasta che non oppone particolare resistenza, esse dovrebbero essere deviate solo leggermente e diffuse sulla parete di fondo. La misura di questa deviazione può far risalire alla distribuzione degli elettroni all’interno del loro piccolo panettone. Ovviamente, ci si aspettano deflessioni di pochi gradi. Teniamo presente che gli atomi sono considerati pieni e quindi vi deve essere un effettivo attraversamento di materia da parte delle particelle alfa.
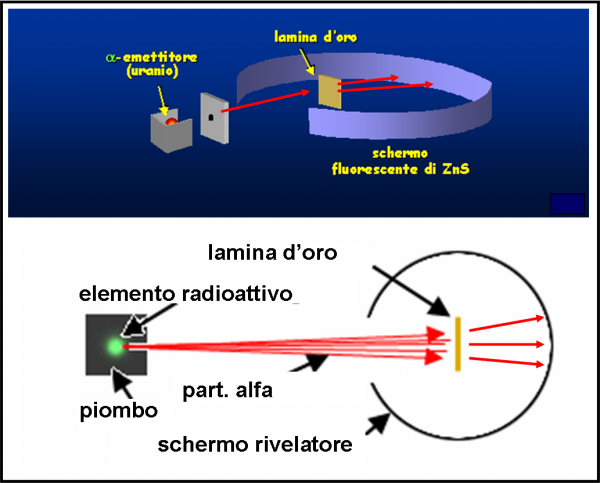
Ciò che, invece, capita è del tutto inatteso. Molte particelle non vengono assolutamente deviate, mentre altre mostrano deviazioni maggiori di 90°, ossia tornano letteralmente indietro!
La Fig. 8 mostra ciò che si ci attendeva con l'atomo di Thompson, colpito dalle particelle alfa, e quello che invece succede. L’atomo deve avere, quantomeno, delle zone veramente vuote e altre talmente concentrate da far rimbalzare letteralmente le particelle. Lo stesso Rutherford dice: “E’ un evento incredibile. E’ come se avessi sparato con un fucile contro un foglio di carta velina e fossi colpito dal proiettile che è stato respinto indietro”
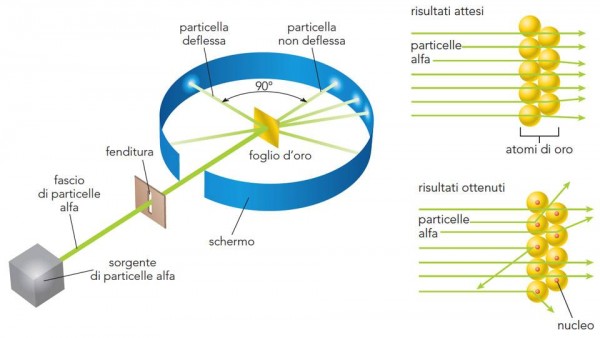
Rutherford interpreta così i risultati dell'esperimento:
la maggior parte delle particelle alfa sono passate senza problemi attraverso le regioni più esterne degli atomi, mentre le particelle restanti devono aver rimbalzato contro qualcosa, all’interno degli atomi, che sia molto piccolo, ma estremamente denso e di carica positiva.
Ciò sconfessa l’ipotesi che l’atomo sia una sfera omogenea e poco densa, ma fornisce gli elementi per una nuova ipotesi: “l'atomo deve avere un nucleo positivo”.
Utilizziamo quel poco che sappiamo sulle funzioni per vedere come esse siano utilissime per descrivere fenomeni fisici d’avanguardia (per l’epoca).
Per analizzare l’urto tra particella alfa e il nucleo d’oro, possiamo fare riferimento allo schema della Fig. 9.
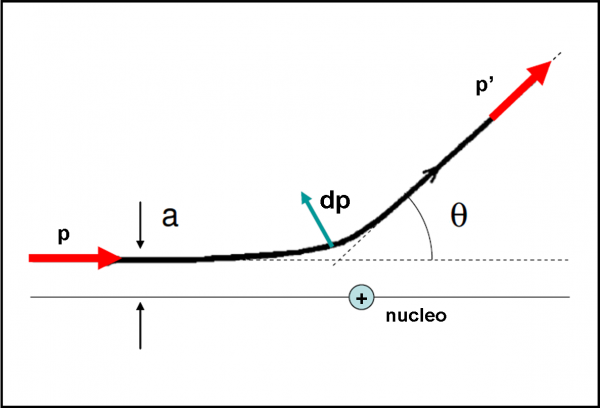
Dall’analisi esatta del problema, molto complesso, risulta che la traiettoria effettivamente seguita dalla particella è un’iperbole, con fuoco nel nucleo dell’atomo d’oro. La distanza a tra il fuoco e l’asintoto orizzontale dell’iperbole (ossia la traiettoria della particella alfa prima dell’incontro ravvicinato) viene chiamato parametro d’urto. Cosa capita alla particella? Essa cambia la sua quantità di moto p a causa della forza repulsiva del nucleo e continua secondo l’asintoto individuato dalla direzione di p’. Per valutare questo spostamento si può usare l’angolo ϑ, ossia l’angolo di deflessione.
E’ facile concludere “qualitativamente” che più è grande il parametro d’urto e minore è l’angolo. Per parametri d’urto molto piccoli, invece, l’angolo può superare i 90° e, quindi, la particella può tornare indietro. In poche parole, abbiamo una famiglia di iperboli che descrive perfettamente l’interazione tra particella alfa e nucleo atomico, come mostrato dalla Fig. 10. Servono o non servono le funzioni?
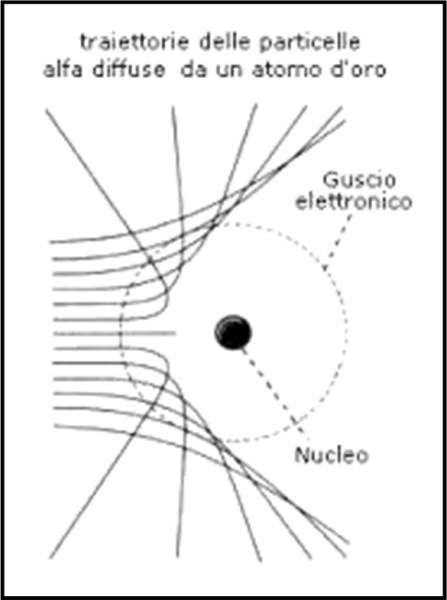
La situazione è stata semplificata di molto, ma dà un’idea più che sufficiente di ciò che ha dedotto velocemente Rutherford. Si può anche illustrare facilmente, in Fig. 11, la relazione tra angolo di deflessione ϑ e parametro d’urto a. La linea rossa indica l’angolo di 90°, ossia il valore limite per il rimbalzo completo delle particelle alfa. E’ il celebre backscattering di Rutherford, ossia il “rimbalzo”.
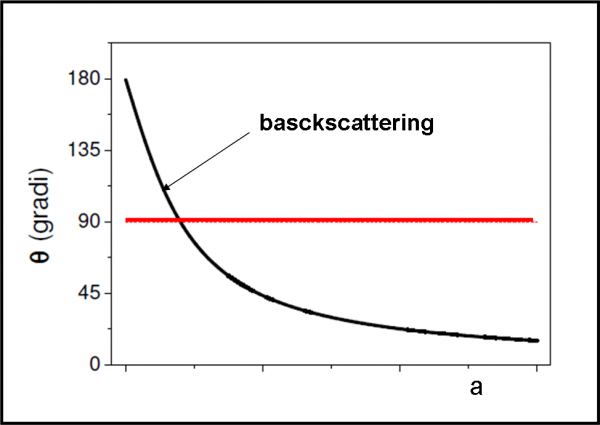
Ovviamente, è un evento che capita molto raramente e per saperne di più potreste sempre chiedere a Feynman e alla sua QED. Potremmo, infatti, formulare l’evento nel seguente modo: una particella parte da A (sorgente delle particelle alfa) e deve tornare in A dopo aver “toccato” la lamina d’oro (non è molto diverso dalla riflessione sul vetro, ormai ben conosciuta…). Le lettere sono sempre le stesse e la parola finale è descrivibile con i diagrammi di Feynman (non è cosa ovvia, però…). Ovviamente, l’ampiezza è molto piccola… ma l’evento può capitare…
Chiudiamo questo inciso che è servito a far vedere come tutto è collegato a tutto, sia a livello QED sia a livello di studio elementare (o quasi) di funzioni. Meditiamoci sopra…
Ricapitolando, l’esperimento porta Rutherford alle seguenti conclusioni: le particelle alfa, nella maggior parte dei casi, oltrepassano la lamina d'oro senza subire deviazioni. Ciò significa che non incontrano alcun ostacolo sul proprio cammino e che, quindi, l'atomo deve essere formato prevalentemente da spazio vuoto. In qualche caso, però, le particelle vengono deviate e in rarissimi casi addirittura riflesse. Ne segue che l'intera carica positiva dell'atomo deva essere concentrata in un "nocciolo" piccolissimo e centrale: il nucleo.
E’ ora facile enunciare il suo modello atomico:
L’ atomo è essenzialmente vuoto: poiché le particelle alfa hanno una massa circa 7 500 volte maggiore rispetto a quella di un elettrone, per passare indisturbate oltre la lamina (e ciò accade per più del 99% di esse) non devono trovare ostacolo nelle masse dei singoli atomi di oro. La massa di ciascun atomo d'oro deve essere concentrata in una regione particolare: il nucleo.
Il nucleo è carico positivamente: deve essere 104-105 volte più piccolo di quello dell'atomo e deve essere carico positivamente: solo così si possono spiegare le notevoli deviazioni nella traiettoria (anche con riflessione indietro, ossi con angoli ϑ maggiori di 90°) di un numero limitato di particelle alfa.
Il modello è di tipo planetario: dal momento che, in condizioni ordinarie, la materia è impenetrabile, bisogna supporre che gli elettroni debbano occupare, in qualche modo, la periferia dell'atomo (lo spazio intorno al nucleo). In prima approssimazione gli elettroni possono essere immaginati come i pianeti attorno al Sole.
L’ atomo è elettricamente neutro: il numero degli elettroni, carichi negativamente, deve essere uguale a quello delle cariche positive presenti nel nucleo, per cui l'atomo, nel suo complesso, è neutro.
Lo stesso Rutherford chiama protoni le più piccole particelle positive: il nucleo di un atomo neutro deve essere formato da tanti protoni quanti sono gli elettroni.
Malgrado l’esperimento e le conclusioni siano davvero rivoluzionarie e geniali, il modello di Rutherford dura molto poco. Basta la fisica classica a condannarlo rapidamente e ad aprire la strada alla MQ.
L’elettromagnetismo dice che ogni volta che una carica viene accelerata essa deve irradiare energia. Nel modello di Rutherford gli elettroni ruotano attorno al nucleo e, quindi, devono possedere un’accelerazione centripeta (notate l’importanza del moto circolare uniforme) e quindi devono emettere energia. Perdendo energia in modo costante devono anche rallentare il loro moto e, di conseguenza, la loro orbita decade (come capita per i satelliti artificiali e non solo). Prima o poi gli elettroni devono cadere sul nucleo. Questo, però, NON capita. Se gli elettroni cadessero sui nuclei, la materia stessa si “sgonfierebbe” (in realtà lo fa, ma sotto condizioni molto particolari, come sappiamo bene dalla “morte” di certe stelle…). Non solo, però: le osservazioni dicono che le emissioni elettromagnetiche risultano discontinue (righe spettrali delle stelle).
Dagli atomi alle stelle
Come vedete siamo arrivati a bomba, ossia alle righe spettrali. Siamo entrati, senza quasi accorgercene, nel mondo dei giganti e le stelle rappresentano la prosecuzione della storia dell'atomo. Inoltre, solo la Meccanica Quantistica (MQ) può spiegarci sia il modello atomico che le righe degli spettri stellari. E’ ora che intervengano i pacchetti d’energia e la nuova interpretazione di Bohr. Come si fa a toccare la materia senza avere i rudimenti base della MQ?
E’ perfino un peccato che l’atomo di Rutherford sia durato pochissimo, talmente è innovativo. Forse è per questo che si continua a usarlo in tante scuole? Tuttavia, questo è il destino delle grandi scoperte: mettono subito in condizioni di fare il passo successivo. Rutherford, perciò, ha avuto un’importanza fondamentale e le grandi scoperte non si misurano con la loro durata temporale. Oltretutto, il succo del modello (nucleo e elettroni molto distanti) rimane inalterato anche nell’ottica dell’onnipresente principio d’indeterminazione di Heisenberg .
Con l’atomo di Rutherford, una piccola meraviglia che, però, non può esistere, siamo arrivati a un punto fondamentale nella fisica della materia (microcosmo) e nell’astrofisica (macrocosmo). Non possono più fare a meno una dell’altra! Fino a questo momento, in qualche modo, la chimica si è occupata delle interazioni tra le particelle più piccole (atomi), mentre l’astrofisica ha cercato di capire cosa fossero le stelle e come si potessero leggere le loro caratteristiche attraverso l’unica informazione che ci mandano (la luce).
Tuttavia, la luce fa parte delle interazioni tra le particelle del microcosmo e la faccenda si annoda e si ingarbuglia sempre più. In un momento in cui sembrava che la fisica classica avesse spiegato quasi tutto (soprattutto dopo le equazioni di Maxwell) si aprono da tutte le parti problematiche nuove e rivoluzionarie. Molte di loro evidenziano la polvere che in qualche modo è stata messa sotto al tappeto, come la catastrofe ultravioletta, un argomento collegato strettamente agli spettri stellari. Non parliamo poi delle righe spettrali che si rifanno direttamente alla consistenza del modello atomico.
Quasi senza accorgersene nasce la meccanica quantistica, una soluzione matematica prospettata da Planck, quasi per disperazione, in cui lui stesso non crede e considera un artefatto di comodo. D’altra parte proprio a chi sta rivoluzionando la meccanica classica a seguito delle scoperte di Maxwell (e che sa utilizzare al meglio le trasformazioni già prospettate da Lorentz) si deve la prova decisiva di quanto Planck avesse ragione. Sì, proprio lui, Einstein, che sarà sempre un duro oppositore delle leggi assurde che sembrano negare una realtà deterministica. “Dio non può giocare a dadi”, diceva, intendendo che ogni cosa capita a seguito di un'altra, in una continua successione di causa ed effetto. E, invece, questa nuova “scienza” sembra dimostrare che la Natura agisce a casaccio, scegliendo senza alcuna regola e affidandosi solo alle probabilità che un evento possa accadere.
Insomma, un momento meraviglioso di menti sublimi e di idee innovative, di cui è quasi impossibile fare una storia temporale, tanto le varie scoperte si intrecciano e si annodano una con l’altra. Sembra di rivivere, nella Scienza, il periodo artistico del primo quattrocento. Mai tanti artisti geniali erano vissuti assieme e avevano incrociato le idee personali in una visione sempre più generale e coerente. Non vi era un vero maestro, dato che ognuno portava un mattoncino in più alla rivoluzione tecnica della prospettiva e alla visione solida e potente dell’uomo che, per la prima volta, prendeva coscienza di sé e poteva calpestare il suolo reale che la prospettiva gli aveva creato.
Così sta succedendo nei primi del novecento, in cui si intrecciano teorie diverse, esperimenti al limite dell’assurdo e visioni sempre più generali che permettano al microcosmo di spiegare ciò che capita nel macrocosmo. Una rivoluzione concettuale prima che fisica.
Tante parole per dirvi che non è facile scegliere come andare avanti nella storia della scienza dell’inizio del nuovo secolo. Per spiegare una cosa bisogna darne per assodata un’altra e viceversa. Se lavorassimo solo sull’evoluzione della meccanica quantistica perderemmo di vista lo sviluppo degli studi delle stelle come entità macroscopiche. Se parlassimo dell’evoluzione stellare avremmo comunque bisogno delle righe spettrali e quindi della meccanica quantistica. Per non parlare della meccanica relativistica che, se apre una nuova visione dello spazio-tempo, si oppone duramente a molte conclusioni quantistiche, prima fra tutte l’impossibilità della gravità, la forza che domina il macrocosmo, di trovare un posto ben definito all’interno delle regole dell’infinitamente piccolo.
Siamo, quindi a un bivio fondamentale nella storia dell’astrofisica e della fisica della materia. Ognuna ha bisogno dell’altra. Non ci resta che andare avanti di pari passo e mantenere un continuo collegamento tra le due discipline, come fossero due elettroni che si scambiano l’informazione attraverso il loro messaggero luminoso, il fotone. In fondo, le due avventure, vedono proprio il fotone come personaggio principale.
Da un lato dovremmo continuare con l’atomo di Bohr e le sue successive rielaborazioni sempre più inserite nella MQ e dall’altro dovremmo parlare delle stelle, dei loro meccanismi esistenziali e -soprattutto- di ciò che la luce può raccontarci, proprio perché nasce dalle interazioni esistenti nel microcosmo.
Spettroscopia e struttura atomica sono, quindi, due facce della stessa medaglia. La spettroscopia riesce a raccontarci le stelle, le loro differenze e le loro caratteristiche “personali”. Tuttavia, essa ha bisogno della luce e della sua produzione, la quale può essere descritta e analizzata solo con la perfetta conoscenza della struttura dell’atomo. D’altra parte, l’interesse verso l’atomo nasce proprio perché ha ripercussioni sul mondo macroscopico. Il messaggio troppo criptico e codificato delle stelle può essere decodificato solo conoscendo come lavora l’atomo e come interagisce con i propri simili. Lo studio delle stelle ha bisogno di sapere come funziona il mondo atomico; il mondo atomico viene studiato per riuscire a leggere i messaggi stellari.
Seguiremo quindi due strade, apparentemente diverse, ma sempre abbracciate l’una all’altra. Faremo salti enormi, con riferimenti reciproci costanti, proprio perché manderemo avanti l’evoluzione scientifica e i suoi problemi in tempo quanto più possibile reale. Tuttavia, è un modo del tutto arbitrario, scelto per scopi utilitaristici e di semplicità divulgativa. Se qualcuno mi chiedesse quanto Paolo Uccello ha ricevuto da Masaccio e quanto Paolo Uccello ha dato all’arte del quattrocento, non esisterebbe nessuna formula esatta capace di legare il passaggio d’informazione dal primo al secondo e dal secondo agli altri, e via dicendo. Ognuno riceve e trasmette secondo regole non quantificabili.
Forse dovremmo inserire una moltiplicazione di ampiezze di probabilità e poi fare delle somme vettoriali… Forse la mente lavora proprio secondo le regole della QED (l'elettrodinamica quantistica)… Fermiamoci qui, se no cadremmo nella speculazione filosofica. Ricordiamo, però, che comunque si proceda nella spiegazione della Scienza, esiste sempre un filo comune che tiene il tutto ben legato e niente è veramente indipendente da qualsiasi altra “cosa”.
In pratica, l’atomo quantistico ci permette di risolvere la catastrofe ultravioletta, di capire cosa sono le righe spettrali, perché ve ne sono tante e non una sola, e perché esse rappresentano la carta d’identità preziosissima e indispensabile per conoscere una stella e le sue azioni. Con tutte queste informazioni legate al messaggio luminoso, solo apparentemente “semplice” e sempre uguale, si può ricostruire non solo la posizione spaziale e temporale delle stelle, ma anche la loro intrinseca differenza di composizione e di modo di vivere.
D’altra parte, le condizioni che esistono all’interno di queste “enormi stufe” ci informano sulla situazione a cui devono sottostare gli atomi e ci permettono di comprendere sempre meglio le loro interazioni. Un serpente che si morde la coda? Beh… la Scienza porta sempre a questo risultato, dato che cerca, in modi solo apparentemente diversi, di spiegare la stessa identica cosa: la Natura.
In conclusione, come già accennatovi, sospenderemo per un po' la struttura dell’atomo e andremo sulle ... stelle. Salteremo da un argomento all’altro, ma non preoccupiamoci: anche gli elettroni vivono … saltando!
Via libera alla luce (ma per poco)
Immaginiamo di tornare indietro nel tempo, a una data particolarmente importante e fondamentale per la storia dell’Universo. Anno più, anno meno, sono trascorsi 380 000 anni dal Big Bang o da qualsiasi altra cosa abbia gonfiato quello strano palloncino spazio-temporale in cui è nata la materia e che è diventato l’Universo. Non vogliamo cercare di spiegare cosa è successo in questo intervallo ancora in larga parte sconosciuto e misterioso. Oltretutto, anche se ci sforzassimo di vedere cosa succede in questo periodo non vedremmo niente per una ragione molto semplice: non esiste la luce o -molto meglio- la luce non riesce a lanciarsi verso il futuro e quindi non può arrivare fino a noi. Troppa confusione e troppo poco spazio a disposizione! Ci basta sapere quello che si è formato: sicuramente gli atomi dei primi due elementi della Natura, i più leggeri, ossia l’idrogeno (soprattutto) e l’elio. Vi è anche un po’ di litio, ma possiamo anche trascurarlo.
L’Universo è nato caldissimo, ma si è velocemente raffreddato e gli elettroni si sono inseriti attorno ai nuclei atomici creando strutture neutre (le cariche positive e quelle negative si equivalgono). Elettroni, nuclei, raffreddamento… parole che ormai conosciamo. Per adesso, interessiamoci poco di loro dato che gli atomi neutri non sono in grado di produrre luce e la luce, come vedremo, è l’unica fonte di energia che noi uomini riusciamo a cogliere dalle stelle. Pensiamola anche come l’unica informazione che ci viene regalata.
Immaginiamo, quindi, questi atomi dispersi in uno spazio enorme per le loro dimensioni, troppo piccole anche se il loro numero è incredibilmente alto. Hanno raggiunto una stabilità interna e hanno tutto lo spazio che vogliono a loro disposizione. Anzi, questo spazio continua a dilatarsi e a ingigantirsi, mentre loro rimangono sempre gli stessi. La materia è quella che è e non può cambiare: nulla si crea e nulla si distrugge. Sembra tutto perfetto e, invece, l’Universo è in una situazione veramente critica.
Tanto lavoro per nulla
Ha lavorato in modo frenetico, violento, caotico, rapidissimo e ora si trova in una fase di stallo che sembrerebbe senza via d’uscita. Per un attimo siamo riusciti a “vederlo”, ossia abbiamo ricevuto la luce di ciò che stava stabilizzandosi. Poi anche quell’energia è finita (nessuno può rilasciarla e rimane circoscritta all’atomo) e la calma regna sovrana. Un atomo qui, un atomo là, senza interazioni e sempre più lontani gli uni dagli altri. Ma, soprattutto, un Universo che non potrebbe inviare luce e informazione. L’astronomia finirebbe, ma non solo. Non nascerebbero le stelle, i pianeti, la vita biologica e gli unici abitanti sarebbero tantissimi atomi di idrogeno, molti meno di elio e qualche atomo di litio. La storia dell’Universo sarebbe già terminata.
In realtà, ogni atomo ha una potenzialità enorme, vi sono forze potentissime che lo tengono unito e ne comandano la struttura, ma a che pro? Tutta fatica inutile, dato che queste forze o agiscono solo su distanze infinitesime oppure hanno bisogno che le cariche non si annullino, ossia che gli atomi cessino di essere neutri. Proprio questa condizione aveva permesso, poco tempo prima, di inviare, per un tempo molto breve, la luce verso un futuro in cui, però, nessuno potrebbe, ora, essere in grado di riceverla. Un destino buio, una specie di nebbia impenetrabile.
Insomma, ci vorrebbe proprio una bacchetta magica per cambiare una situazione che sembra senza speranza. Fortunatamente, questa bacchetta magica esiste già fin dall’inizio di tutto (o poco dopo) ed è la quarta forza del Cosmo, la meno potente, ma quella che meglio lavora sulle distanze enormi dell’Universo: la gravità. E’ la gravità, da sola, che permette agli atomi di non seguire una vita monotona, ripetitiva, senza alcuna interazione tra di loro. E’ la gravità che permette di far nascere le stelle, gli attori fondamentali del Cosmo, gli unici capaci di creare elementi più complessi dell’idrogeno e dell’elio, i primi oggetti che hanno permesso agli atomi di emettere nuovamente luce e accendere un Universo che ormai sembrava inesorabilmente spento.
A molti, forse, questo inizio sembra tutto fuorché scientifico. Assomiglia a un romanzo di fantascienza o a una triste favola per bambini, in attesa che qualche buona fata rompa un tragico incantesimo. Non abbiate paura, lentamente arriveremo a discutere in termini matematici e fisici, ma cosa sia una stella e cosa capiti nel suo interno sono proprio episodi simili a quelli di una meravigliosa avventura. La Natura, ricordiamocelo sempre, segue regole molto semplici che siamo spesso noi a complicare, non riuscendole a capire.
Alla gravità basta la massa
Vediamo, allora, cosa s’inventa la buona fata chiamata gravità. Essa dipende dalla distanza tra gli atomi (nel senso che si indebolisce velocemente per distanze crescenti) e dalla loro massa. Più la massa è grande è più la forza si fa sentire. Gli atomi sono piccoli e la loro massa è altrettanto piccola, ma esiste, dato che essi sono i primi e unici esempi di materia che popolano il Cosmo.
Sono anche tantissimi e relativamente vicini per la gravità. Tanto vicini da far scattare una mutua attrazione. Possiamo immaginarci il momento straordinario in cui i primi due atomi si sono uniti tra loro, e poi altri due e così via in ogni zona dell’Universo. Due atomi uniti hanno più massa di uno soltanto e la loro forza di gravità riesce ad attrarne un altro e poi un altro ancora. E più la massa cresce e più atomi vengono raccolti, come se si stesse usando un… aspirapolvere.
A questo punto, facciamo una precisazione molto importante e più tecnica. Gli atomi non sono distribuiti in modo ordinato e omogeneo. Fosse così, nemmeno la gravità riuscirebbe a fare qualcosa. Fortunatamente, vi sono zone in cui ve ne sono di più e più vicini, regioni più dense, dove la gravità riesce a lavorare con maggiore velocità e facilità. Sono i nuclei in cui sorgeranno le immense galassie, che già si intuiscono in quella breve luce che l’Universo ha mandato verso il futuro prima che tutto si addormentasse. Oggi la chiamiamo rumore cosmico di fondo, appena percettibile a causa del suo lunghissimo viaggio fino a noi, ma pensiamola come la prima e ultima luce (e informazione) che proviene dai luoghi dove la gravità, in un buio completo, riesce a mettere insieme il maggior numero di atomi e a far “rinascere” l’Universo.
Non ci vuole poi molto a farlo rinascere, basta ionizzare di nuovo gli atomi, ossia strappargli gli elettroni e dare il via nuovamente all’emissione dell’energia luminosa. Cose queste che vedremo molto meglio in seguito, ma che rappresentano l’essenza del nuovo Universo, ciò che ci ha permesso di nascere e di ammirarlo e analizzarlo. L'Universo rinasce grazie alla voglia di movimento degli irrequieti elettroni! Che migliore legame ci può essere tra l'infinitamente piccolo e l'infinitamente grande?
Le condizioni sono cambiate
E’ doveroso fare una precisazione. Abbiamo visto che la prima luce dell’Universo è stata anche l’ultima, prima del periodo del grande buio, dovuto alla presenza di soli atomi neutri. Perché la prima, però? All’inizio violento del Cosmo, si è, teoricamente, in condizioni ideali, dato che tutti gli atomi sono ancora ionizzati. Gli elettroni sono liberi di muoversi, di accelerare e di rallentare. Producono fotoni, ossia la luce, che dovrebbe dominare su tutto e tutti e invece… è un periodo che non possiamo vedere. Purtroppo, lo spazio è ancora troppo piccolo e l’energia luminosa, lanciata dagli elettroni che vagano in questo oceano di particelle a stretto contatto tra loro, non riesce a districarsi.
Sbatte a sinistra, rimbalza a destra e via dicendo. In poche parole rimane intrappolata e può uscire allo scoperto solo quando gli elettroni, finalmente, si uniscono ai nuclei. Qualcuno potrebbe chiedere: “Perché, allora, si è dovuto aspettare che gli atomi si ionizzassero di nuovo, quando abbiamo visto che si creava la luce, ma che essa veniva bloccata completamente?”.
La ragione è semplice: lo spazio è ormai molto più grande e la materia si è concentrata in zone particolari. Una volta uscita da una stella (e poi dalle nubi e dalle galassie) la luce è libera di viaggiare senza trovare più ostacoli verso noi che la osserviamo. E’ riuscita a farsi strada con un sistema “a staffetta” (come vedremo tra poco) attraverso le nubi di materia spesse e dense sì, ma non certo come l’Universo primitivo. La luce è ancora abbastanza “forte” e viva per proseguire lungo strade prive di veri ostacoli. Ogni tanto viene assorbita da qualche corpo; viene riemessa e cambia strada; altri riescono a deviarla soltanto; la maggior parte, però, è in grado di raggiungere tutto il Cosmo e portare ovunque il suo unico e preziosissimo messaggio, con le informazioni sul luogo dove si è formata.
Cerchiamo di vedere la luce proprio come un intricato sistema di comunicazione, l’unico che permette di far conoscere i luoghi di partenza. Una rete informatica enorme e perfettamente funzionante. Basta solo saper interpretare i codici che è costretta a usare (i messaggeri della luce sono molto, molto piccoli e devono compattare al massimo l’informazione…).
Appurato, quindi, che la ionizzazione è adesso utilissima non ci resta che ottenerla. Una cosa, però, è il dire e un’altra è il fare. La gravità da sola lavora molto bene in questa specie di battaglia contro la monotonia, ma, come in tutte le battaglie, ha bisogno di un avversario degno di lei. E se lo crea, praticamente, da sola.
Una battaglia contro se stessa
Mentre la gravità agisce e avvicina sempre più milioni, miliardi, miliardi di miliardi di atomi, questi tentano di ribellarsi al loro “schiacciamento”. E come se troppe persone entrassero in un vagone di una metropolitana, senza che il flusso di viaggiatori diminuisca. L’unico modo di reagire é cercare di farsi largo, di agitarsi attraverso spinte e urti. In poche parole, di contrastare, con il movimento continuo, l’ingresso di altre persone in uno spazio ormai quasi saturo. Analogamente gli atomi, agitandosi sempre di più, esercitano una pressione che contrasta l’arrivo di nuovi atomi spinti dalla gravità reciproca.
Si è ormai creato, all’interno di una nube densa di materia gassosa, fatta di idrogeno e di elio, un nucleo centrale che è soggetto a una compressione terribile da ogni parte. Gli atomi di questo nucleo sono in movimento frenetico, l’unico metodo che hanno per opporre resistenza alla gravità.
In qualche modo, stanno reagendo come possono e tutto ciò che permette di agire prende il nome di energia (in realtà, definire energia è una delle cose più difficili anche per gli addetti ai lavori). In questo caso è energia di movimento e prende il nome di energia cinetica delle particelle coinvolte nella lotta per resistere alla gravità. E’ una situazione abbastanza peculiare: la gravità spinge gli atomi a unirsi per rompere la monotonia dell’Universo, ma gli stessi atomi cercano di non essere schiacciati in un abbraccio che potrebbe disintegrarli del tutto. Sì, la gravità è una magnifica “fata”, ma non sa dosare la propria “forza”: una vera fortuna per il Cosmo e i suoi attori principali.
L’energia cinetica EC si quantifica abbastanza bene dato che dipende dalla massa della particella e dal quadrato della velocità acquisita. Possiamo anche scriverla facilmente secondo una formula matematica:
EC = 1/2 mv2
Più la massa cresce, più si agita e meglio si oppone alla gravità che tende a farla sprofondare verso il centro del nucleo ultra affollato. Questa è l’energia che le particelle contrappongono a quella gravitazionale, che dipende essenzialmente dalla posizione della particella rispetto al centro della nube che la sta attirando verso di lei con una massa sempre crescente. Un'energia che può chiamarsi potenziale, in quanto esiste "in potenza" e dipende solo dalla posizione che assume chi la possiede.
Un teorema per descrivere una pace sempre in bilico
Una lotta titanica che porta a un equilibrio descritto da un teorema che è un po’ come il “prezzemolo” per una moltitudine di fenomeni fisici: il teorema del viriale. Esso dice che l’equilibrio si ottiene quando l’energia potenziale è uguale al doppio dell’energia cinetica delle particelle. Teniamo sempre presente che le due energie non nascono separate, ma sono forme diverse della stessa “cosa”. La forza di gravità tende a far collassare la nube verso il centro e, come conseguenza, nasce l’agitazione che cerca di bilanciarla. Se non ci fosse la gravità non nascerebbe nemmeno l’agitazione delle particelle. L'energia non può sparire o distruggersi, può solo trasformarsi.
Raggiunto questo equilibrio possiamo dire che la battaglia è finita? Nemmeno per sogno! La pace si mantiene attraverso un’opera continua di mediazione. La massa raggiunta dalla nube che evita il collasso continua a crescere e di conseguenza deve crescere anche il movimento delle particelle che evitano la catastrofe. L’equilibrio è frutto di una lotta continua. Basterebbe poco a romperlo. Se vincesse la gravità le particelle sarebbero schiacciate oltre ogni limite di resistenza e gli stessi nuclei atomici sarebbero distrutti. Se gli atomi si agitassero troppo, la nube esploderebbe rilanciando indietro tutte le particelle compresse. E’ ora di chiamare l’energia cinetica delle particelle con un altro nome, molto più comune e utile per lo scopo della nostra avventura: energia termica. In poche parole, quando aumenta l’energia cinetica aumenta la temperatura del gas che sta subendo la gravità.
Il teorema del viriale può essere enunciato in un altro modo: si raggiunge l’equilibrio quando l’energia dovuta alla gravitazione si trasforma in energia termica. Anzi, è sufficiente che l’energia termica sia uguale alla metà dell’energia gravitazionale. In parole povere, solo la metà dell’energia gravitazionale serve a scaldare il gas. Cosa succede all’altra metà? Non può certo sparire, dato che l’energia può solo trasformarsi. Bene, nessun problema, viene rilanciata verso lo spazio esterno. Sì, è proprio quella di cui abbiamo bisogno per accorgersi che sta nascendo una stella: l’energia luminosa (meglio ancora elettromagnetica). Questo è il segnale che l’agitazione del gas ha creato la luce, ossia gli atomi si sono nuovamente ionizzati, dando via libera agli elettroni e ai loro figli, i fotoni.
L’Universo sta rinascendo e questa fase prende proprio il nome di fase di reionizzazione. Possiamo tirare un sospiro di sollievo: le stelle si stanno formando e la luce, nuovamente creata, è stata lanciata verso lo spazio.
Le stelle stanno nascendo e lo vogliono far sapere
Come possiamo definire una stella in parole estremamente semplici: una “macchina” capace di fare aumentare la temperatura di un ammasso di particelle.
Possiamo fermarci qui, dato che lo scopo di questa chiacchierata non è quello di entrare nei dettagli della formazione stellare e di tutti i vincoli che sono necessari al suo completamento. Ci basta aver visto che i parametri fondamentali per descrivere una stella sono già stati definiti: massa, temperatura e luminosità. La massa indica quanta sia la materia che sta collassando sotto l’effetto della forza gravitazionale; la temperatura indica lo stato di agitazione delle particelle di materia (ossia la loro energia cinetica); la luminosità indica la parte di energia che non si trasforma in energia termica e viene lanciata verso lo spazio. Quest’ultima è l’unica che ci manda informazioni. Le altre due ci sono (teoricamente) vietate. Tuttavia, la luce ha in sé tutte le informazioni della stella, comprese le sue impronte digitali
La magnifica avventura della mente umana è riuscita a leggere il messaggio luminoso e a risalire alla massa e alla temperatura e, come una cascata conoscitiva, anche all’età e alla composizione chimica. Dapprima solo con l’osservazione dei fenomeni macroscopici e poi entrando letteralmente nei fenomeni che avvengono a livello atomico. Tutto ciò analizzando solo la luce, ossia cercando di estrarre tutte le informazioni contenute in quel messaggio estremamente conciso e tutto da decodificare. Proprio la spettroscopia ci dà la chiave per comprendere il vero significato di quell’energia che ha viaggiato per decine, centinaia, migliaia, milioni, e miliardi di anni. Un’energia simile a una bottiglia lanciata da un naufrago lontanissimo o, ancor meglio, simile a un “pacchetto” ricco di informazioni. Vedremo quanto la parola “pacchetto” sia perfettamente azzeccata.
In realtà, esiste un altro parametro molto importante che non abbiamo ancora definito, ma che è strettamente legato alle altre grandezze: il raggio di una stella. In altre parole, conoscere il raggio vuol dire sapere come si distribuisce la materia all’interno della stella, ossia qual è la sua densità. A parità di massa, la densità cresce o decresce inversamente a ciò che fa il raggio: più è piccolo e più le particelle sono schiacciate all’interno della stella.
Non possiamo, però, lasciare la stella solo in balia di energia potenziale gravitazionale ed energia cinetica delle particelle. Quest’ultima non basterebbe di certo a contrastare, a lungo, la gravità. L’aumento della temperatura è solo il modo per arrivare allo scopo finale di una stella vera e propria. Quando la temperatura sale sufficientemente i nuclei atomici vengono coinvolti in modo pesante e riescono ad andare contro la loro voglia di tranquillità. Entrano in gioco le forze più segrete della materia, quelle limitate a distanze irrisorie per il metro umano: le forze nucleari. Esse sono in grado di produrre un’energia spaventosa, proprio quella che ci vuole per bilanciare la gravità che non potrebbe che vincere in tempi anche relativamente brevi. Un’energia che proviene attraverso una trasformazione che sembra miracolosa per il mondo macroscopico in cui viviamo: la trasformazione di materia in energia.
Solo questa permette alle stelle di vivere e mantenere acceso -e a regime- il loro motore per milioni o addirittura molti miliardi di anni. Tutto dipende dalla temperatura, dalla massa, dalla densità, ossia sempre e soltanto dagli stessi parametri già definiti e che sono strettamente legati tra loro. La sopravvivenza dei corpi più giganteschi dell’Universo dipende essenzialmente da ciò che riescono a fare i corpi più piccoli del Cosmo. Un’avventura veramente “globale”, dove tutti gli attori hanno la stessa importanza. Uno per tutti e tutti per uno!
Se la spettroscopia ci permette di analizzare in dettaglio le singole stelle e riuscirle a classificare secondo i loro caratteri “somatici”, non dimentichiamo che essa, in fondo, ha lo scopo di riuscire a legare tra di loro i parametri fondamentali, quali luminosità (l’unica cosa osservabile, ricordiamocelo sempre) e la temperatura, ad esempio. Questo legame permette di descrivere la vita di una stella e di prevedere il suo futuro e di descriverne il passato. Un legame che è descritto mirabilmente dal celeberrimo diagramma di Hertzsprung-Russell. La spettroscopia permette proprio di costruire questo diagramma fondamentale, oltre che vedere i singoli oggetti attraverso un “microscopio” eccezionale, capace di mostrarci come si muovono gli elettroni, proprio i “costruttori” della luce.
Questi movimenti lasciano un segno peculiare, delle vere e proprie impronte digitali di ogni elemento o composto presente all’interno delle stelle. La faccenda funziona così bene che ormai tutti gli oggetti dell’Universo sono analizzati attraverso questa tecnica pratica e concettuale insostituibile.
Il messaggio delle stelle ovvero la voce degli elettroni
Iniziamo, allora, il nostro viaggio nella spettroscopia sapendo ormai bene cosa significa: decodificare il messaggio ultra-compresso inviatoci dalle stelle. Vedremo che vi è una catastrofe incombente, come spesso accade in tante avventure a lieto fine. In questo caso la catastrofe ha un nome: catastrofe ultravioletta. Essa compare nella sua drammaticità dopo che la spettroscopia è già nata e ha dato informazioni eccezionali. Una catastrofe sempre latente, però, lasciata quasi da parte, cercando di chiudere gli occhi per non rendersi conto della sua esistenza. In fondo si riusciva lo stesso a comprendere molto bene tante cose. Quando si è finalmente affrontata di petto, la sua soluzione ha fatto nascere la meccanica quantistica e gli elettroni hanno dominato la scena insieme ai loro messaggeri, i fotoni.
Avanti, allora, cominciando, ancora una volta, dal grande Newton…
Viva la luce, l’unica informazione che riusciamo a ricevere dalle stelle e dagli oggetti dell’Universo che non siano alla portata degli altri nostri quattro sensi. Qualcuno potrebbe dire: “Non è vero! Quando ci mettiamo al Sole sentiamo molto caldo e la nostra pelle può anche bruciare. Il tatto è stimolato e come…”. No, non confondiamo l’effetto con la causa, perché questo errore ci permetterebbe di misurare la temperatura di una stella solo attraverso l’esposizione alla sua luce e magari con un termometro casalingo.
A parte il fatto che il Sole è l’unica stella che riesce a stimolare altri sensi e non solo la vista, proprio perché è decisamente molto vicina, resta il fatto che l’aumento della nostra temperatura corporea è una reazione a seguito dell’arrivo sulla nostra pelle della luce solare. Il messaggio, che il nostro corpo traduce come può, è sempre lo stesso, quello portato dai fotoni. Non conviene perciò utilizzare i nostri sensi, con gravi rischi per la salute, ma è molto meglio affidarsi a strumentazioni più accurate e sicure. Questo lo avevano capito fin dall’antichità.
Il vetro non trasforma la luce
Una volta, purtroppo, l’unico strumento umano che poteva catturare l’informazione luminosa era l’occhio. Marchingegno fantastico, ma di portata limitata anche per le sue dimensioni molto ridotte. Le stelle non potevano che restare punti e la loro luce sembrava uguale a quella delle altre. Qualcuna più luminosa, altre molto meno, ma sempre le stesse, ogni notte. Non per niente si immaginava che fossero fisse e immutabili.
Tuttavia, vi era anche quella del Sole e questa si riversava sulla Terra e sull’uomo in modo ben più violento e apprezzabile. Essa, come in fondo quasi tutte le stelle, sembrava avere un colore, molto simile al bianco e dava luogo a giochi naturali che non potevano passare inosservati perfino agli uomini delle caverne. Primo fra tutti l’arcobaleno. I raggi del Sole producevano nel cielo degli archi multicolori, poco dopo una bella pioggia e se la loro inclinazione rispetto all’orizzonte era sufficiente bassa.
Non ci fu certo bisogno di aspettare il genio di Newton per capire il processo che avveniva nell’atmosfera: un raggio entrava all’interno di una gocciolina d’acqua, sospesa in aria, e ne usciva separato in tanti raggi di vari colori (sette o sei, ma in realtà di tutte le sfumature che vanno dal violetto al rosso). Cosa analoga succedeva se si utilizzava un pezzo di vetro che venisse attraversato dalla luce solare.
Qual è stata, allora, la grande scoperta di Newton che ha dato il via a tutta la storia della luce che ancora oggi coinvolge e sconvolge gli scienziati (per altre e più sottili ragioni). Fino ai suoi esperimenti con un prisma di vetro triangolare, si pensava che fosse la sostanza vetro (o acqua o cose simili) a trasformare la luce bianca in luce colorata. In altre parole, che fosse una caratteristica del mezzo attraverso cui era costretta a passare la luce. Un fenomeno del tutto indipendente dalla luce che ci mandava il Sole.
Capite la grande limitatezza di questa conclusione? La luce, al massimo, avrebbe dato informazioni su ciò che attraversava e se lo attraversava, ma non certo su cos’era lei prima di toccare il vetro. Newton invece dimostrò che il prisma mostrava ciò che era insito nella luce e che il nostro occhio non riusciva a percepire. Era la luce stessa a essere composta di vari colori e il prisma non faceva che aiutare la loro separazione. I suoi esperimenti furono decisivi e inattaccabili.
Uno su tutti. Dopo aver prodotto la separazione dei vari colori, egli riuscì, attraverso una stretta fenditura, a farne proseguire solo uno. Esso fu nuovamente inviato contro un prisma. Se fosse stato il prisma a trasformare la luce, questa “selezione” sarebbe stata di scarsa importanza e la luce si sarebbe di nuovo scomposta. Ciò che osservò Newton fu, invece, che quel colore, separato dagli altri, non subiva alcuna trasformazione e usciva dal prisma tale e quale a come era entrato. I colori non dipendevano dal prisma, ma proprio dalle caratteristiche intrinseche della luce. Il prisma metteva solo in evidenza che quella che sembrava una luce “bianca” era invece formata da tutti i colori visibili all’uomo (ma non solo da quelli, come vedremo tra poco).
Non vogliamo certo raccontare tutta la storia dell’ottica e dei continui cambiamenti di idea sulla sua natura. Resta, comunque, il fatto indubbio che Newton capì la sua complessità e aprì la strada alla sua interpretazione. Ricordiamo che ai suoi tempi non si conoscevano gli elettroni e nemmeno i loro messaggeri e l’atomo era un’idea astratta, mal sopportata dalla Chiesa. Tuttavia, si sapeva, finalmente, che era composta da vari colori e che la loro unione portava al colore bianco.
Tutte quelle stelle lontane inviavano luce, anche se in modo molto flebile e, quindi, tutte quelle stelle inviavano lo stesso tipo di informazione. Riuscire a capire cos’era la luce voleva dire avvicinarsi all’Universo e ai suoi attori principali.
Ancora oggi, la luce è l’unica vera informazione che l’Universo ci manda e all’inizio di questa chiacchierata abbiamo visto che essa non è altro che una forma di energia o di informazione che si crea in un ambiente molto particolare, dove vi è una battaglia feroce e leale tra gravità e agitazione di particelle invisibili. Questa informazione deve viaggiare per miliardi di anni rimanendo comunque visibile anche se affievolita. Ci vogliono, perciò, messaggeri robusti o -ancora meglio- poco influenzabili da ciò che incontrano nel loro viaggio. Sappiamo benissimo che meno siamo grassi e pesanti e molto più facilmente riusciamo a muoverci nel traffico. Lo stesso deve avvenire per le particelle più piccole dell’Universo: meno massa hanno e meglio si muovono. La luce segue proprio questa strada. Al punto da non avere massa…
Una particella molto ambigua
Prima di vederne le caratteristiche più particolari dobbiamo, però, capire se è o non è una particella. La risposta è, anche oggi: “NI”. Tra Newton e noi, la luce ha cambiato spesso e volentieri natura: si è cominciato a vederla come corpuscoli e poi come qualcosa di simile alle onde del mare. Poi addirittura entrambe le cose assieme, anche se un altro grande genio della Fisica, Einstein, dimostrò senza ombra di dubbio che la luce DOVEVA comportarsi come particelle anche se non possedeva massa. Con lui nasceva il fotone, il vero e proprio messaggero luminoso, ma le sue caratteristiche rimanevano ancora molto ambigue, non solo per la nostra incapacità a capire, ma proprio per la sua natura reale.
Come già detto non possiamo fare la storia delle conquiste dell’ottica, sia da un punto di vista ondulatorio (intesa come onde) che particellare (come tanti piccolissimi proiettili), e nemmeno entrare più di tanto nella sua natura ambigua che esperimenti fondamentali, veri e propri capolavori “artistici”, hanno dimostrato inequivocabilmente, come quello della doppia fenditura di Feynman.
Per far ciò bisognerebbe parlare a fondo della meccanica quantistica, il cui nome mette subito paura non solo agli allievi ma agli stessi insegnanti. No, non la descriveremo in questo articolo, perché occorrerebbero libri e libri, dato che la meccanica quantistica può essere compresa solo dopo aver imparato perfettamente la meccanica e la fisica classica. Solo a quel punto, il girare pagina ed entrare in un mondo assurdo e privo di ogni logica comune, può essere un’azione fattibile anche se mai veramente comprensibile. Alla MQ, però, sono già stati dedicati molti articoli che ne danno un'idea generale abbastanza completa.
Per poter capire un dipinto di Picasso è necessario conoscere molto bene la storia dell’arte figurativa. Solo così si capisce la rivoluzione della nuova visione del mondo. Lo stesso Picasso è riuscito a esprimerla acquisendo prima una perfetta conoscenza mentale e tecnica dell’arte che l’aveva preceduto. Insomma, nessuno nasce “imparato”!
Quello che potremo fare è solo estrarre da lei alcune conclusioni fondamentali, quelle che ci permettano di capire un po’ meglio cosa sia realmente la luce e perché è in grado di darci un numero incredibile di informazioni anche se sembra solo stuzzicare il nostro occhio. Non solo capire, però, ma anche decodificare l’informazione che viene trasmessa in modo criptico ed estremamente compresso (potrei dire “ultra-zippato”).
La luce è movimento
In realtà, se torniamo all’inizio dell’Universo, e alle varie fasi di ionizzazione e di stabilità degli atomi, dovremmo aver già capito che per avere luce, ossia energia visibile a grandissime distanze, è necessario che vi sia movimento delle particelle che compongono la materia. Devono agitarsi le molecole, gli atomi e ciò che costituisce gli atomi. In questo modo ci si oppone alla gravità, cresce la temperatura della materia e gli elettroni possono vivere in modo più o meno indipendente, ionizzando il gas.
Solo il movimento è capace di far nascere i messaggeri luminosi, quelli che abbiamo chiamato fotoni. In realtà, non è il solo modo di produrre luce, ma per quello che vogliamo descrivere può bastare. Come abbiamo visto, la luce non è altro che energia “in più”, che può tranquillamente disperdersi e lasciare le stelle. Ne basta la metà a continuare la lotta, come ci ha dimostrato il teorema del viriale che stabilisce l’equilibrio.
Cerchiamo, adesso, di essere veramente semplici, a rischio di mancare in precisione, ma questo è uno scotto che bisogna pagare nella divulgazione della Scienza. Essa è un serpente che si morde sempre la coda e se si vuole approfondire qualcosa si continua a girare e aggiungere, a ogni giro, nozioni sempre più vaste e complesse. Cerchiamo, perciò, di limitarci senza commettere errori troppo vistosi.
Tutto nasce dal moto degli elettroni che vengono “eccitati”, ossia agitati, dalla temperatura. La loro agitazione può fargli abbandonare il loro atomo e permettergli di muoversi a piacimento attraverso la materia, accasandosi altrove oppure no. Al limite, possono solo spostarsi un po’ in alto e un po’ in basso nella loro configurazione attorno al nucleo atomico (questa doppia possibilità è alla base della spettroscopia, tenetela bene a mente). E’ tutta questione di energia che gli viene data. In qualche modo è, quindi, un problema di temperatura che si raggiunge.
Non pensiamo, però, che una volta liberi di muoversi gli elettroni possano fare quello che vogliono. Sappiamo bene che sono ancora all’interno di una stella, di una massa immensa e densissima. In qualche modo ricorda l’Universo precedente alla prima luce, quando le particelle si scontravano tra loro in modo continuo e caotico senza riuscire a seguire una strada precisa.
Gli elettroni sono obbligati a frenare e ad accelerare ogni volta che passano vicino a nuclei positivi o ad altri elettroni. A volte vengono attratti, a volte respinti. Sta agendo una forza molto potente, l’interazione elettromagnetica, quella che mette di fronte particelle di carica positiva e negativa.
Per comprenderla meglio, fatemi fare un semplice esempio, a portata della nostra vita quotidiana, che ci rimanda ancora una volta a Newton e alla sua “mela”. Se una mela si stacca da un albero (che cerca di tenerla stretta a sé attraverso forze che legano molecole e atomi tra loro) cade al suolo. Essa segue quello che le ordina la forza di gravità terrestre. Ma non solo la mela. Qualsiasi oggetto dotato di massa viene attratto, di più o di meno, se entra nella sfera di influenza di una massa molto più grande. Possiamo dire che questa massa (nel nostro caso, la Terra) esercita la sua attrazione in uno spazio estremamente vasto attorno a lei. Gli oggetti che entrano in questo spazio subiscono la sua gravità. Questo spazio possiamo considerarlo come un campo da gioco, dove agisce un un’unica regola: quella di puntare verso il centro. Questo campo viene chiamato campo gravitazionale.
Anche le particelle positive e negative creano un campo da gioco, che si chiama campo elettromagnetico. Esso regola i movimenti di ciò che entra al suo interno e che ha una carica. Immaginiamolo come un oceano in cui non si vedano onde perché troppo piccole per le nostre possibilità o perché siamo troppo in alto. Tutto sembra tranquillo e stabile. Ma, scendendo sempre più in basso, magari usando una barca, ci accorgeremmo che le onde ci sono e come! Esse si sommano, si annullano, seguono direzioni qualsiasi o flussi particolari. Insomma una vera tempesta.
Chi è causa questa agitazione? Proprio le particelle cariche che si fanno sentire attraverso il loro continuo movimento. E’ come se ogni particella creasse un’onda particolare che si scontra con le onde delle altre particelle in modo apparentemente caotico. Bene, queste onde che si propagano potrebbero rappresentare abbastanza bene la luce. Gli elettroni, i più piccoli e quindi quelli che si muovono di più, causano queste vibrazioni nel campo da gioco e ogni vibrazione è un messaggio che mandano ai loro simili e a quelli di segno opposto. In un caso li avvisano di stare attenti, di tenersi a distanza perché due cariche negative devono respingersi; nell’altro, invece, comunicano che possono avvicinarsi dato che le cariche sono opposte e forse potrebbero nuovamente accasarsi.
Fatica inutile se la temperatura è troppo alta e il loro movimento è frenetico. Devono perciò deviare, accelerare, frenare e ogni volta che lo fanno creano una vibrazione che si trasmette alle altre particelle che, a loro volta, la trasmettono ad altri elettroni in uno scambio continuo di informazioni. Alla fine, dopo grande fatica e dopo molto tempo, qualche vibrazione, le ultime che si sono formate, escono dalla lotta tra gravità e agitazione e possono viaggiare nel Cosmo. In questo tipo di approccio non resta che concludere che i fotoni, ossia i messaggi mandati attraverso le vibrazioni, anzi le stesse vibrazioni, sono solo e soltanto onde di una mare composto praticamente di vuoto, ossia privo di un materiale, come l’acqua, che possa far propagare l’onda.
La luce, come abbiamo già detto, è stata a lungo pensata così. Purtroppo, però, non è vero ed essa, spesso e volentieri, si concretizza in particelle capaci di far sentire la propria presenza. Non resta allora che pensarla come entrambe le cose e dare alle vibrazioni una descrizione ben diversa dalla solita. Esse non sono onde reali, ma onde di probabilità. In poche parole, esse rappresentano tutte le possibili posizioni che un fotone (intesa come potenziale particella) può occupare dopo che è stato creato da un elettrone. Una vibrazione che ci dice solo dove è più facile o più difficile localizzare la particella, la bottiglia con dentro il messaggio codificato.
Cercate di accettarlo come un dato di fatto, dato che per capire (o meglio descrivere) la situazione bisognerebbe entrare nella dinamica delle particelle, descritta dalla elettrodinamica quantistica (QED per gli amici) e non è cosa che si può riassumere in poche righe o in poche pagine (è già, comunque, stato fatto in questo blog). Ognuno cerchi di vedere il fotone come preferisce: non sbaglierà mai di molto. Tuttavia, non si meravigli se ogni tanto il nostro amico cambierà la propria natura, ossia il proprio “stato”.
Fortunatamente, le situazioni più critiche e ambigue sono quelle che avvengono all’interno della folla, al centro delle stelle. Lasciamo pure che facciano quello che vogliono, che si comportino in un modo o nell’altro. Quando i più fortunati iniziano il loro viaggio verso di noi non hanno più incontri particolarmente importanti e possiamo immaginare che percorrano delle traiettorie rettilinee. In altre parole, questa è la traiettoria più probabile.
La direzione di arrivo è proprio quella di partenza, dopo aver -ovviamente- eliminato tutti i fastidi grandi e piccoli dovuti alla nostra atmosfera che è, nuovamente, molto affollata anche se non in modo frenetico come gli interni stellari. Capite anche benissimo perché spesso e volentieri si preferisce ricevere l’informazione luminosa al di fuori dell’atmosfera, attraverso occhiali speciali che stiano a un’altezza sufficiente (parliamo, ovviamente, dei telescopi spaziali).
Tutto questo discorso per dire che ciò che riceviamo dalle stelle è un messaggio ricco di informazioni e di energia (in fondo, è la stessa cosa), che nasce all’interno delle stelle, ma che si riferisce soprattutto a ciò che capita nei loro strati superficiali, poco prima di potersi muovere senza troppi inconvenienti.
Tutto molto bello e affascinante… ma sarebbe veramente fantastico poter costruire una stella in laboratorio per capire meglio come l’informazione si crea, si trasforma, si sovrappone e si lancia verso l’esterno. Bene, ciò, fatte le dovute proporzioni fisiche e mentali, è possibile. Questa stella in miniatura che ci permette di simulare la loro luce si chiama corpo nero.
Non ci resta, allora, che capirlo nel miglior modo possibile e vedere come descriverlo. Se ci riuscissimo potremmo estrapolare i risultati ai loro “cugini” giganteschi e riuscire a decodificare i messaggi che ci mandano.
Un corpo nero è un corpo che non esiste in Natura e che non è nemmeno nero. E’ un qualcosa di ideale che, però, si riesce a costruire abbastanza bene in laboratorio. Possiamo considerarlo come un corpo che assorbe tutta la luce che riceve senza rifletterla (da qui il nome di “nero”). Tuttavia, l’energia deve conversarsi e, di conseguenza, il corpo deve in qualche modo riemettere l’energia che ha assorbito.
Tu dai una cosa a me e io do una cosa a te
Come può avvenire questo processo? Bene, in modo molto semplice: l’energia elettromagnetica assorbita aumenta la temperatura del corpo che acquista energia termica, ossia mette in agitazione le particelle microscopiche. Agitazione vuole dire energia cinetica che dà luogo a energia elettromagnetica che abbandona il corpo. Questo processo si chiama irraggiamento e non è altro che l’emissione di onde elettromagnetiche (i fotoni, insomma), generate dall’agitazione delle particelle ossia dalla temperatura raggiunta. Molto simile a ciò che avviene all’interno delle stelle…
A seconda della temperatura, varia la frequenza delle onde elettromagnetiche, ossia la loro energia. Ad esempio, a temperatura ambiente vengono emesse onde infrarosse (ed è per questo che gli occhiali infrarossi permettono di vedere gli esseri viventi anche di notte); oggetti molto freddi emettono onde radio; oggetti molto caldi onde ultraviolette fino ai raggi X e gamma. Questi esempi ci ricordano un fatto che a volte crea qualche confusione. La temperatura di un corpo si alza attraverso l’assorbimento di energia elettromagnetica (come quella che arriva dal Sole) e, dopo l’assorbimento, il corpo riemette energia elettromagnetica. Che differenza c’è tra le due? Presto detto: la frequenza delle onde.
Prendiamo come esempio proprio il corpo nero. Se è nero vuol dire che non emette nel visibile se no lo vedremmo colorato. Però, riceve luce visibile per scaldarsi. In altre parole, riceve onde con la frequenza del visibile e riemette nell’infrarosso, invisibile ai nostri occhi. Ne segue che il corpo nero può benissimo non essere nero. Lo è soltanto a temperatura ambiente. Se alziamo la sua temperatura inizia a colorarsi perché emette nel visibile e passa dal rosso, al giallo al blu. Poi, nell’ultravioletto, ricominciamo a non vedere più niente, ma il corpo continua a emettere (e come!) anche a lunghezze d’onda sempre più corte (frequenza maggiore).
Un piccolo inciso che verrà utile tra non molto. Le stelle hanno una temperatura tale da inviare la luce soprattutto in certe lunghezze d’onda che i nostri occhi riescono a vedere. In altre parole, il massimo della radiazione avviene quasi sempre nella stretta zona dello spettro elettromagnetico che noi chiamiamo visibile (dal rosso al violetto). Basterebbe che fossero molto più fredde o molto più calde e non riusciremmo a vederle. Oggi sappiamo che esistono corpi celesti che emettono in una zona vietata ai nostri occhi, ma ormai abbiamo costruito gli occhiali necessari allo scopo. Tuttavia, le abbiamo scoperte solo perché hanno la giusta temperatura. Insomma, hanno fatto di tutto per essere viste. Ah… questi fotoni! hanno proprio saputo che frequenza scegliere. Non possiamo che ringraziarli… se no saremmo vissuti senza stelle e senza astronomia… Un attimo, però. Quasi sicuramente il discorso va visto al contrario. Le stelle emettono dove gli pare e piace, ma sono stati i nostri occhi a essere predisposti per “leggere” proprio quel tipo di lunghezza d’onda. Beh… forse sì, dato che le stelle sono nate prima di noi. Torniamo al nostro corpo nero che emette dove vuole.
In realtà, il corpo emette in tutte le lunghezze d’onda, ma ne “preferisce” qualcuna, legata alla temperatura che ha raggiunto. Bene, è ora di spiegarci meglio e di introdurre un corpo nero sperimentale quasi perfetto.
Costruiamone uno abbastanza “ideale”. Come ci mostra la Fig. 12, basta utilizzare una larga cavità completamente isolata dall’esterno con un foro piccolissimo che permetta di fargli entrare l’energia. I fotoni che entrano cominciano a sbattere contro le pareti, si riflettono e un po’ alla volta vengono “assorbiti”. La loro energia si trasferisce in energia cinetica, ossia in calore. Di sicuro non possono più uscire se il foro è abbastanza piccolo. Sarebbe come trovare un ago in un pagliaio. Continuiamo a inviare energia fino a raggiungere una temperatura costante all’interno della cavità. Siamo in condizioni di equilibrio termico.
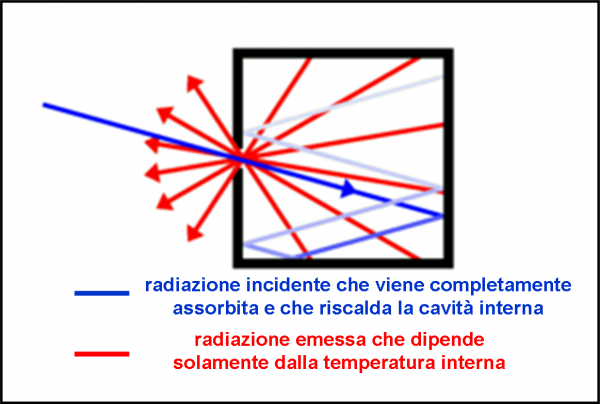
Il foro diventa, adesso, anche lo spioncino per studiare l’energia che viene emessa. Infatti, l'energia cinetica (calore) causa urti e libera fotoni, ossia energia elettromagnetica. Basta farla passare attraverso un prisma (ma c’è di meglio) e vedremmo che questa radiazione si distribuisce in funzione della lunghezza d’onda λ (o della frequenza ν, che non è altro che ν = c/λ, dove c è la velocità della luce). In altre parole, si può misurare quanta energia viene emessa per piccoli intervalli di lunghezza d’onda o di frequenza (come preferiamo). Si ottiene uno spettro della luce, o -meglio- uno spettro elettromagnetico come quello che ci mostra la Fig. 13, che riporta l’energia emessa in funzione della lunghezza d’onda per tre diverse temperature. Ci torneremo presto…
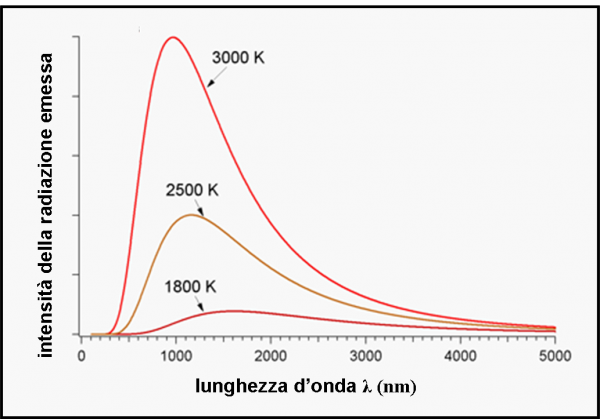
Un chiarimento per non creare confusione. A volte, si vedono disegni che illustrano il corpo nero e il suo irraggiamento come quello di Fig. 14. In questo caso, si simula visivamente ancora meglio una stella, dato che il riscaldamento avviene all’interno della sfera cava, mentre sono poi le pareti esterne a emettere la radiazione. Ciò vuol dire che le pareti esterne non sono isolate. Tuttavia, la soluzione presentata precedentemente ha il vantaggio di avere un punto d’uscita ben determinato del flusso luminoso ed è quindi più facile da analizzare. Comunque, il “succo” dell’esperimento è esattamente lo stesso.
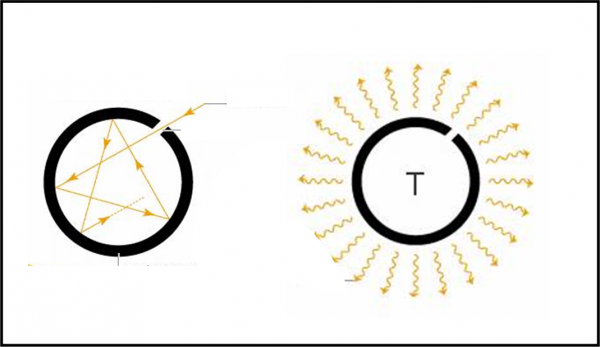
La tremarella che non si vede
Descriviamo ancora meglio l’irraggiamento termico. Ripetere non fa mai male. Per fare stare veramente fermo un corpo dovremmo essere alla temperatura di 0 K, ossia allo zero assoluto (-273 °C). In questo caso, tutte le particelle più piccole si possono considerare ferme. Consideriamo un atomo con i suoi elettroni piazzati attorno a lui in una quiete perfetta. Cominciamo ad aumentare la temperatura. Gli atomi iniziano a muoversi, a vibrare (da fuori non possiamo certo vedere questa vibrazione… la sentiremmo solo attraverso la temperatura). Un atomo comincia a urtare un altro atomo. Gli elettroni sono poco pesanti e sono i primi a essere coinvolti nello scontro. Sono loro ad assorbire l’energia cinetica che gli è stata trasferita nell’urto. Qualcuno salterà rimanendo all’interno dell’atomo e poi tornerà al suo stato iniziale riconsegnando l’energia ricevuta attraverso l’emissione di energia elettromagnetica, ossia emettendo un fotone. Il fotone si muove e sicuramente urta un altro atomo e gli trasferisce la sua energia cinetica. Il gioco continua e nascono fotoni di tutte le energie, ossia di tutte le frequenze. In altre parole, ognuno può essere visto come una vibrazione del campo elettromagnetico di lunghezza d’onda diversa.
Più la temperatura sale e più questo continuo movimento fatto di urti, di elettroni che saltano o addirittura se ne vanno prima di essere magari catturati da un altro atomo, produce sempre più fotoni di tutte le lunghezze d’onda e quindi aumenta la radiazione luminosa, ossia la radiazione termica (dato che è causata dall’aumento della temperatura).
Ormai gli elettroni sono tutti coinvolti nella frenetica danza fatta di spinte sempre più violente. In conclusione, più aumenta la temperatura e più aumenta sia l’energia totale che il corpo emette, sia l’energia che ogni fotone può raggiungere (legata, come già detto) alla frequenza dell’oscillazione.
Tutta questa bellissima e invisibile battaglia tra particelle è ciò che il corpo nero può mostrarci attraverso la misura della radiazione termica emessa e della sua distribuzione. L’unico parametro che causa questo risultato è la temperatura a cui è stato riscaldato. Il discorso non è così semplice, perché le varie lunghezze d’onda dell’emissione dipendono da cosa si scontra: molecole, atomi o solo elettroni. In ogni modo i risultati relativi all’emissione termica di un corpo nero sono indipendenti dal tipo di materiale e dalla forma del corpo che emette. Chi comanda è solo la temperatura e, quindi, anche l’agitazione delle particelle, senza curarsi della loro carta d’identità chimica.
Per la campana e il suo "picco" conta solo la temperatura
Anche se in modo abbastanza empirico, è stato possibile, già nella seconda metà dell’ottocento, descrivere, con due semplici formule, la dipendenza della luce emessa da un corpo nero in funzione della temperatura raggiunta. In particolare, si è stabilito che l’energia totale della luce emessa per unità di tempo (ossia la potenza) è proporzionale alla quarta potenza della temperatura. In parole matematiche:
E = σ T4
dove σ è una costante. Più esattamente, si ricava che il numero di fotoni emessi nel’unità di tempo va con il cubo della temperatura, mentre la loro energia media dipende linearmente da essa. Moltiplicando numero di fotoni per la loro singola energia media otteniamo la quarta potenza enunciata prima. Questa legge prende il nome di legge di Stefan-Boltzmann e lo stesso nome viene dato anche alla costante σ.
Questa legge, importantissima, ci dice quanta energia si produce globalmente al variare della temperatura. Più la temperatura cresce e più energia si produce. Risultato abbastanza comprensibile e logico.
Fatta questa preliminare precisazione, possiamo ricavare un’altra legge empirica molto importante, ricordando che la capacità di oscillare di un fotone è legato alla sua energia. Tanto più è energetico è tanto più corto è il suo periodo di vibrazione e quindi anche la sua lunghezza d’onda. In semplici parole: energia e lunghezza d’onda di un fotone sono inversamente proporzionali. Tuttavia, abbiamo appena detto che l’energia di un fotone dipende in modo lineare dalla temperatura. Ne segue una relazione fondamentale per il corpo nero: tanto più grande è la temperatura tanto più piccola è la lunghezza d’onda. Questa relazione, chiamata legge di Wien, vale, in particolare, per la lunghezza d’onda in cui è massima l’emissione. Questa legge ci dice che per ogni temperatura si ha un certo valore della massima radiazione luminosa. Sappiamo, però, che ad ogni lunghezza d’onda è associato un certo colore. Ne segue che a ogni temperatura è associato un ben determinato colore in cui si ha il massimo di emissione. La formula di Wien si scrive:
λmax = k/T
dove k è una costante. Parlando di massimo d’emissione in funzione della lunghezza d’onda non possiamo fare a meno di parlare, in modo più approfondito, dello spettro elettromagnetico del corpo nero, per una certa temperatura, mostrato in Fig. 13. Esso, come già detto, non è altro che la distribuzione dell’intensità della luce emessa da un corpo nero in funzione della lunghezza d’onda. Proprio quella che si riesce a costruire analizzando la luce che esce dal famoso forellino. Gli esperimenti mostrano molto bene che essa segue una specie di campana, raggiungendo un valore massimo per una certa lunghezza d’onda. Variando la temperatura varia anche lo spettro, seguendo le due leggi appena formulate. Tuttavia, c’è qualcosa che non va…
Ricapitoliamo brevemente: la legge di Stefan-Boltzmann dice che l’energia totale (quella dell’intera campana) è funzione della temperatura, mentre quella di Wien ci dice che il massimo di questa “campana” si sposta verso lunghezze d’onda maggiori per temperature decrescenti. Mettendole assieme, si può dire che la campana sposta il suo massimo verso lunghezze d’onda maggiori, per temperature decrescenti, e che la campana, nella sua totalità, si abbassa. Fin qui tutto bene, come mostra la Fig. 13.
Magnifico. Due leggi molto interessanti e molto utili per il nostro scopo, dato che legano molto bene temperatura, lunghezza d’onda ed energia luminosa. Tuttavia, sarebbe molto bello saper descrivere matematicamente la “campana”, osservata direttamente negli esperimenti. In altre parole, cercare di andare oltre alla legge di Stefan-Boltzmann, e calcolare teoricamente non solo l’energia totale, ma quella relativa a ogni singola lunghezza d’onda.
Trafficando con le varie grandezze in gioco, Wien sembrava aver trovato una buona rappresentazione (Fig. 15). Purtroppo, però, andava bene per piccole lunghezze d’onda, ma falliva per grandi lunghezze d’onda. In qualche modo lui aveva lavorato su un gas composto da molecole, dato che ancora non si conoscevano le interazioni tra le particelle più piccole.
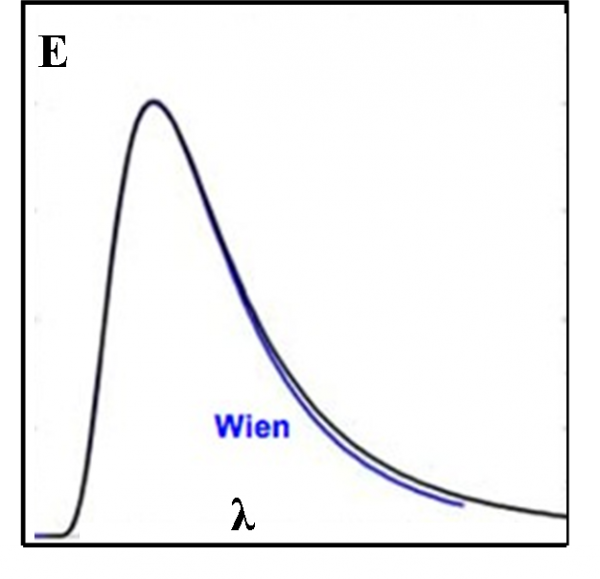
Una catastrofe infinita
Utilizzando la teoria elettromagnetica sviluppata da poco, si giunse anche a una legge teorica che stabiliva come l’energia della singola lunghezza d’onda dovesse essere direttamente proporzionale alla temperatura, ma inversamente proporzionale alla quarta potenza della lunghezza d’onda. Essa si chiama legge di Rayleigh-Jeans. Come già detto, essa è una legge teorica, basata sulle nuove teorie dell’elettromagnetismo e dovrebbe funzionare, a meno di non ammettere che le teorie così apparentemente perfette siano, invece, ben lontane dalla verità. Riportiamo questa formula teorica che, però, non … funziona assolutamente:
ΔE = C T/λ4
Dove ΔE è l’energia relativa a un piccolo intervallo di lunghezza d’onda e C una delle “solite” costanti (da non confondere con c che è la velocità della luce!).
Essa va benissimo per lunghezze d’onda molto lunghe, ma per lunghezze d’onda sempre più corte (alte frequenze) porta a valori sempre più alti dell’energia. Teoricamente, per una lunghezza d’onda uguale a zero l’energia diventa infinita. E questo non si vede assolutamente negli esperimenti e nemmeno è un risultato ammissibile. La Fig. 16 ci mostra l’andamento che ci si aspetterebbe dalla legge teorica, confrontato con l’andamento reale di un corpo nero: una vera CATASTROFE per l’elettromagnetismo!
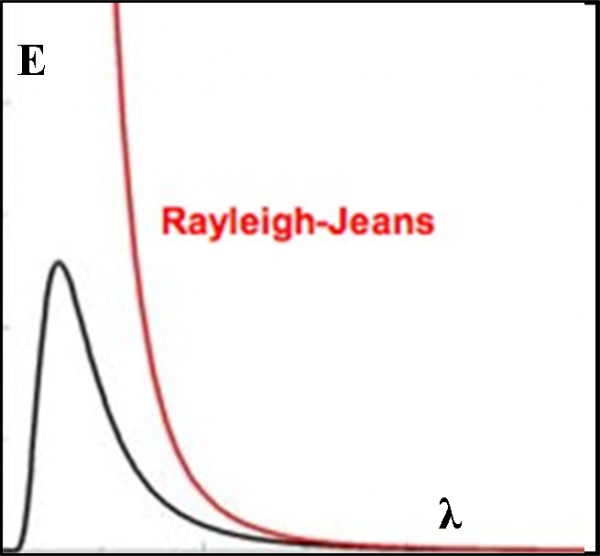
Dato che la parte, subito prima della minore lunghezza d’onda dello spettro visibile, prende il nome di ultravioletto, questo risultato assurdo venne chiamata proprio catastrofe ultravioletta. Il corpo nero era un meravigliosa astrazione che permetteva di legare perfettamente l’energia dei fotoni (e quindi la luminosità) alla temperatura, ma la legge che doveva descrivere questa relazione sembrava portare a una vera “catastrofe” per le piccole lunghezze d’onda.
Tra poco, affronteremo di petto questa problematica che aprirà le porte, quasi senza volerlo, alla meccanica quantistica e al modello atomico di Bohr. Prima di partire in quarta, ragioniamo un attimo su quello che abbiamo ottenuto con il corpo nero e con la sua distribuzione in funzione della lunghezza d’onda, ossia lo spettro. Anche se non riusciamo a spiegarlo con la Fisica Classica, resta pur sempre un risultato fantastico, soprattutto se accompagnato dalle due leggi di Stefan-Boltzmann e di Wien. Vale la pena riproporre in Fig. 17, qualche spettro elettromagnetico di corpo nero, inserendo le lunghezze d’onda del visibile (ossia i colori dell’arcobaleno o del prisma di Newton). A sinistra del visibile abbiamo l’ultravioletto (UV) e a destra l’infrarosso (IR).
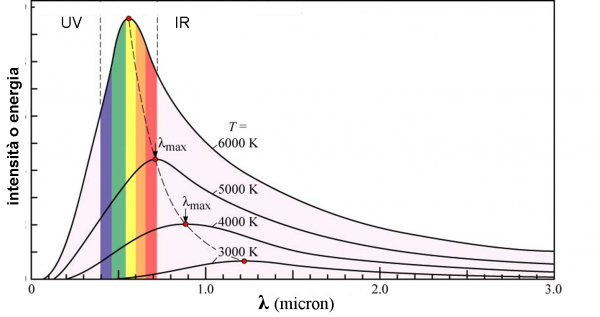
In realtà, lo spettro elettromagnetico è estremamente ampio e la parte visibile è una regione estremamente limitata, come vediamo nella Fig. 18.
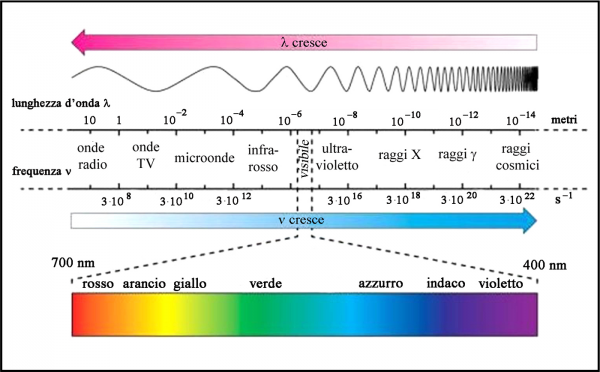
Uno spettro senza regole
Come si vede molto bene dalla Fig. 17, il corpo nero emette secondo uno spettro che sembra descritto da una linea continua. Proprio per questa caratteristica viene chiamato spettro continuo. Uno potrebbe chiedersi perché un corpo caldo emette in questo modo. La risposta sta nel fatto che l’emissione deriva dall’agitazione di un numero incredibile di particelle che modificano in ogni modo la loro energia e, quindi, i fotoni che alla fine lasciano il corpo nero possono assumere qualsiasi lunghezza d’onda, ossia energia. Un mix straordinario che non dipende assolutamente dalla composizione del materiale, ma solo dalla temperatura.
Ovviamente, l’emissione avviene in tutte le lunghezze d’onda, ma non con la stessa intensità. Vedremo tra poco che ciò è legato alla probabilità che si possa fare un salto più o meno energetico. Ad esempio, in certe regioni giocano molto i movimenti molecolari, mentre in altre vengono coinvolti gli elettroni più vicini al nucleo atomico. Insomma, un mix di azioni e reazioni che coinvolgono tutta la struttura delle particelle che compongono la materia. Ovviamente, sotto il controllo unico e generale della temperatura.
Possiamo anche sintetizzare, un po’ rozzamente, la situazione in questo modo: lo spettro continuo dipende dall’interazione tra le particelle agitate dalla temperatura, che avviene in tutti i modi possibili e che, come conseguenza, ripartisce l’energia in gioco senza apparente soluzione di continuità. Esso è prodotto da innumerevoli salti di elettroni liberi, che cioè si muovono tra un nucleo e l'altro. Poiché gli elettroni liberi possono avere energie molto differenti si ottengono fotoni di tutte le lunghezze d'onda (anche se in numero minore o maggiore), che descrivono proprio il "continuo".
Se, invece, abbiamo a che fare con particelle abbastanza isolate e dello stesso tipo, non tutte le energie, e quindi lunghezze d’onda, sono possibili. Esse assorbono energia dai fotoni che le eccitano spostando gli elettroni in modi prestabiliti, e poi la riemettono solo e soltanto secondo regole analoghe, ossia attraverso fotoni con ben determinate lunghezze d’onda. Tutto ciò sempre in base alla temperatura raggiunta, ovviamente. In qualche modo, ogni elemento ha una sua carta d’identità ben precisa. Anzi, come vedremo, ha molte caratteristiche peculiari, delle vere e proprie impronte digitali, le righe spettrali. Un vero spettro stellare è come quello descritto nella Fig. 19, in cui abbiamo considerato proprio il Sole, confrontato con la migliore curva di corpo nero che lo approssima. Quelle righe sono proprio fastidiose e sembrano “sporcare” il nostro spettro. E, invece, sono proprio loro a farci capire come agiscono le stelle e di cosa sono fatte. Ma, andiamo con calma… questa parte la vedremo molto meglio in seguito.
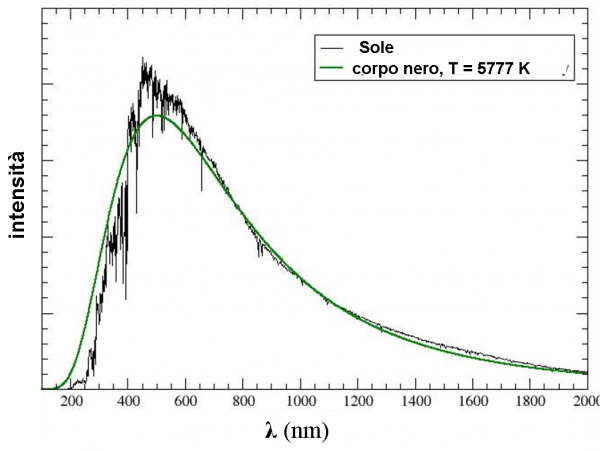
Quale temperatura?
Per adesso, abbiamo già compreso che se il corpo nero potesse essere applicato alle stelle ci permetterebbe di calcolare la temperatura dell’astro, soltanto dalla distribuzione della sua energia o della sua luminosità. Sappiamo, infatti, che ad ogni temperatura corrisponde una ben determinata curva a campana con un certo valore del picco più alto. Sì, ma quale temperatura della stella?
Beh… non certo quella della sua parte più interna, dove l’energia in gioco è spaventosa e dove avviene la vera battaglia tra gravità, energia cinetica e energia nucleare. Tuttavia, ciò che conta è che i fotoni, che partono da quella zona così “calda”, tentino di raggiungere la superficie. Non è facile, come abbiamo già detto, e lo ottengono a passi successivi, aiutati dai fratelli. Ognuno di loro cede la propria energia a qualche elettrone che poi riemette un altro fotone e via dicendo fino a giungere in superficie. Ciò che noi riceviamo, perciò, è relativo alla temperatura della superficie, dato che è lì che si creano i fotoni che raggiungono i nostri telescopi.
Lo stesso, in fondo, capita nel corpo nero. Anzi, abbiamo visto che esso può essere sottilissimo, dato che ciò che comanda l’emissione è la temperatura della parte più esterna. Le condizioni sono analoghe. Non basta, però. Il corpo nero ha la caratteristica di assorbire tutta l’energia che proviene dall’esterno e riemetterla solo in base alla temperatura. La stella è qualcosa di molto simile: non riflette assolutamente niente ed emette solo ciò che le è comandato dall’agitazione delle particelle, atomi o elettroni che siano; ossia, proprio dalla temperatura.
In entrambi i casi l’energia rilasciata dipende solo dalla temperatura dello strato più superficiale.
OK, allora! La prima enorme conquista è stata ottenuta! Analizzando la distribuzione della luce alle varie lunghezze d’onda è possibile, confrontando lo spettro della stella con quello del corpo nero che più gli assomiglia, RICAVARE la temperatura del corpo nero e quindi della stella. Proprio ciò che abbiamo mostrato nella Fig. 19. Fantastico!
La temperatura ha dato il via ai fotoni che non solo ci portano l’informazione luminosa, ma, una volta decodificata, anche la temperatura che li ha aiutati a iniziare il loro viaggio verso di noi. Abbiamo già due grandezze fondamentali: la luminosità (quella che fa splendere le stelle) e la temperatura della loro superficie (senza aver avuto bisogno di un termometro cosmico…).
Due grandezze che possono già permetterci di inserire le stelle in un grafico, avendo due coordinate: luminosità e temperatura. Beh… lo conoscete tutti molto bene: stiamo già abbozzando il celeberrimo diagramma di Hertzsprung Russell.
Prima di andare a vedere cosa succede nelle superfici stellari a causa delle particelle libere di giocare i loro scambi energetici senza essere disturbate da troppi vicini di casa (le righe spettrali), parliamo anche un po’ di colore. Sì, proprio il colore dell’arcobaleno.
Newton (e non solo lui) ci ha mostrato che al variare della lunghezza d’onda varia anche il colore che l’occhio riceve. Sappiamo anche che il nostro occhio copre solo un piccolissimo intervallo dello spettro elettromagnetico. Potremmo dire che esistono colori, ossia lunghezze d’onda, che non possiamo associare a niente di fisicamente recepibile dai nostri sensi. Fortunatamente, l’uomo ha costruito occhi che vedono anche i “colori” relativi a lunghezze d’onda sia cortissime che grandissime.
Tuttavia, per definire la temperatura di una stella può già bastare osservare lo spettro nel visibile. E non c’è nemmeno bisogno di ottenere tutto lo spettro (ricordate il breve inciso che avevamo inserito sulla giusta temperatura delle stelle?). Basta fissare due lunghezze d’onda (ad esempio quella del blu e quella del rosso) e fare la differenza di luminosità. In effetti, due spettri relativi a due stelle di diversa temperatura si spostano uno rispetto all’altro, abbassandosi o alzandosi a seconda della posizione del loro picco. (Ricordiamoci le due leggi di Stefan-Boltzmann e di Wien). Ciò vuole anche dire che se facessimo la differenza tra la luminosità nel blu e quella nel rosso avremmo, nei due casi, valori diversi.
Siamo piuttosto fortunati! Non solo le stelle emettono soprattutto nel visibile, ma non esistono differenze di due colori (scegliendoli bene, ovviamente) che coincidano, se gli spettri sono diversi. Ciò vuol dire che basta considerare questa differenza (indice di colore) al posto della temperatura. Conosciuto l’indice di colore si risale allo spettro corrispondente e quindi alla temperatura. Nella Fig. 20 vediamo due spettri e il relativo indice di colore B-V.
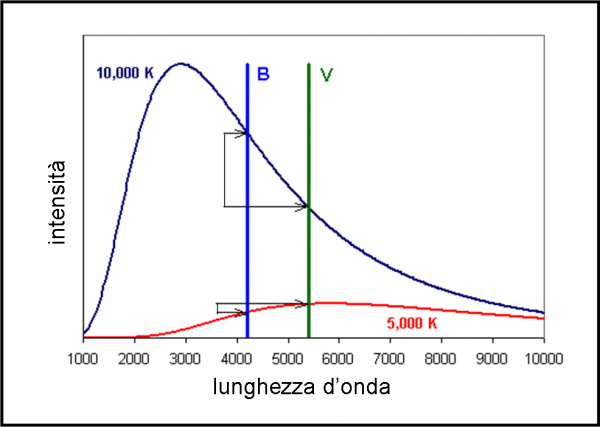
Perché tanta fatica? Perché non sempre è possibile ottenere uno spettro, dato che l’intensità della luce dipende dalla distanza. E’ molto più facile misurare la luminosità in due soli colori (o lunghezze d’onda, ricordiamolo sempre). Il risultato è, però, quasi lo stesso, dato che da questa differenza si può approssimativamente risalire alla temperatura e al diagramma HR precedente. Ecco perché tante volte si vede in ascissa sia l’indice di colore che la temperatura o anche il colore della stella (relativo al punto di massimo dello spettro, che a sua volta è legato alla temperatura).
Bene, le stelle cominciano a essere comprensibili attraverso la loro temperatura e luminosità. Grazie ai fotoni le informazioni sono più di quelle che uno si aspetterebbe guardandole a occhio nudo. Tutto ciò grazie al corpo nero e -soprattutto- alla tecnica della spettroscopia.
Tuttavia, le informazioni contenute nella luce sono ben più numerose. Per andare avanti dobbiamo, però, capire ancora meglio come si muovono gli elettroni, come interagiscono tra di loro e come fabbricano i loro messaggeri luminosi. Per far questo occorre dare un’occhiata alla meccanica quantistica e ai modelli più moderni dell’atomo. Oltretutto, la meccanica quantistica spiega perfettamente perché la catastrofe ultravioletta è una catastrofe solo apparente. Ciò permetterà di descrivere l’andamento dello spettro continuo con una formula perfetta. Il modello atomico si occuperà invece di quelle righe “scure” che sembrano essere solo un rumore noioso nello spettro di una stella. Sarà anche un rumore un po’ fastidioso, ma è un rumore che ci regala un numero incredibile di informazioni…
Vedremo, anche, che i due grandi iniziatori di questa decodificazione completa dell’informazione sono accomunati da una strano destino: il primo (Planck) ha tentato una spiegazione senza crederci affatto (per pura disperazione); il secondo (Einstein) l’ha verificata senza sapere che sarebbe stata l’incubo della sua vita.
L’energia viaggia a “pacchetti”
Torniamo alla ormai ben nota curva a campana e alla sua “catastrofe” ultravioletta. C’è poco da fare, le leggi della fisica classica non permettono di descrivere ciò che si osserva sperimentalmente. Ci deve essere qualcosa di sbagliato nella legge di Rayleigh-Jeans, ma non “troppo” sbagliato se no tutta la fisica precedente sarebbe da buttare al macero. E, invece, sappiamo che per moltissime cose funziona perfettamente bene.
Immaginiamo di avere uno scivolo praticamente infinito che inizi a un altezza comparabile a quella degli aerei di linea (ma anche più in alto). Vicino a lui vi è, invece, una scala che parte e arriva negli stessi punti dello scivolo. Se utilizzassimo lo scivolo, è meglio non pensare a cosa ci potrebbe succedere arrivando al suolo! La velocità acquisita sarebbe incredibile e sarebbe molto difficile raccogliere i nostri pezzetti sparsi di qua e di là. Abbiamo, infatti, acquistato un’energia cinetica enorme. Insomma, ci capita una vera … “catastrofe”. Se, invece, usassimo la scala, scenderemmo molto lentamente ma arriveremmo sani e salvi. L’energia finale sarebbe insignificante, dato che l’abbiamo rilasciata gradino per gradino e non tutta assieme nell’urto finale. Nessuna… catastrofe!
Nulla è effettivamente cambiato, ma ciò che prima sembrava infinita (l’energia) diventa invece praticamente nulla. Qualcosa di simile al corpo nero. La fisica classica (scivolo?) ci dice che a lunghezze d’onda molto corte l’energia tende a essere enorme, mentre l’evidenza osservativa (scala?) ci dice che l’energia è trascurabile. Mi raccomando, non prendete questo esempio troppo alla lettera. Serve solo per capire meglio il concetto di fondo.
L’idea, però, non è male... Perché non pensare che anche l’energia, che viene rilasciata dai fotoni, lavori in modo analogo? In altre parole, potremmo dire che ogni fotone porta con sé l’energia di uno scalino. Non sappiamo, ancora, perché mai dovrebbe funzionare così, ma “per disperazione” potremmo anche provare a fare questa ipotesi campata del tutto in aria, senza alcuna prova sperimentale.
Beh… possiamo anche evitare di fare i conti, dato che ci ha già pensato il signor Planck. Egli ha ipotizzato che a ogni fotone sia associata una certa quantità di energia, che ha chiamato “quanto”. In altre parole lo “scalino”. Tuttavia, gli scalini non possono essere tutti uguali, dato che la loro “altezza” (energia) deve dipendere dalla lunghezza d’onda (o frequenza) del fotone. Deve valere, perciò, una certa legge che regola il rapporto tra energia E e frequenza ν. Chi deve rimanere costante è il rapporto tra queste due quantità, ossia:
E/ν = h
h prende (giustamente) il nome di costante di Planck. Essa permette di misurare l’energia di un “quanto” associato a una certa frequenza. Questa costante è qualcosa di estremamente piccolo e nessuno potrebbe rendersi conto sperimentalmente che l’energia si propaghi a piccoli salti, invece che in modo continuo.
Chi vede strisciare per terra un millepiedi, pensa subito che sia un verme. E, invece, guardandolo bene, si nota che è munito di moltissime zampette. Immaginiamo che ogni paio di zampette sia un pacchetto di energia. Pensate a un millepiedi con le zampette piccolissime e il gioco è fatto. Diciamo un… miliardopiedi.
Questa ipotesi, del tutto artificiosa e senza alcun legame con la fisica conosciuta, permette di evitare la catastrofe ultravioletta. In parole molto semplici: aumentando la frequenza, ogni pacchetto ha un’energia maggiore, ma diminuisce il numero di pacchetti disponibili. Andando verso lunghezze d’onda cortissime l’energia è sempre più alta, ma si hanno sempre meno pacchetti a disposizione. La probabilità che si possa “formare” un pacchetto di energia infinita è zero e quindi l’energia totale in funzione della lunghezza d’onda sale fino a un certo valore massimo per poi scendere di nuovo a zero per lunghezze troppo corte.
Notate che ho usato alternativamente lunghezza d’onda e frequenza proprio per ribadire meglio il concetto che una grandezza è inversamente proporzionale all’altra. Se una cresce, l’altra decresce.
Per una visione ancora più semplice del concetto dei quanti (da prendere con le dovute limitazioni), immaginiamo di avere un pozzo pieno d’acqua e di volerlo svuotare. Lo possiamo fare, però, usando secchi di grandezza crescente durante intervalli di tempo sempre uguali. All’inizio i secchi sono molto piccoli. L’operazione è rapidissima, ma ogni secchiello contiene pochissima acqua. Nel tempo limite siamo riusciti a fare ben poco.
Cambiando dimensioni del secchio le cose vanno un po’ meglio: se ne riempiono di meno, ma ognuno contiene molta più acqua di prima. La quantità totale di acqua, prelevata usando il secondo secchio, è decisamente maggiore. La quantità continua a crescere aumentando le dimensioni del secchio.
A un certo punto, però, i secchi cominciano a pesare un po’ troppo e nel tempo limite riusciamo a tirarne su molti di meno della volta precedente. La quantità totale dell’acqua recuperata inizia a diminuire. Il secchio è ormai molto grande e pesantissimo: nel tempo prestabilito possiamo tirarne su pochissimi. La faccenda continua a peggiorare. Alla fine arriviamo al punto in cui il secchio è talmente grande che non riusciamo nemmeno a tirarne su uno: niente più acqua! Se segnassimo su un foglio la quantità d’acqua che abbiamo estratto dal pozzo in funzione della grandezza del secchio (o della lunghezza d'onda) ci accorgeremmo di aver descritto una curva a campana, propria quella che elimina la catastrofe.
Se, invece, usassimo una pompa aspirante di diametro crescente, troveremmo che la quantità d’acqua recuperata nell’unità di tempo crescerebbe sempre di più. Teoricamente, con la pompa giusta, potremmo prosciugare un intero lago in un intervallo di tempo cortissimo. Insomma, arriveremmo alla … catastrofe. In un caso l'acqua è stata tirata su a pacchetti (secchi), nell'altro in modo continuo (pompa).
Ovviamente, Planck non ha usato né secchi né ha mai dovuto prosciugare un pozzo, ma è riuscito, seguendo l’ipotesi fantascientifica del pacchetto di energia, a ottenere una formula che descrive perfettamente la campana della distribuzione di energia al variare della lunghezza d’onda (o della frequenza). Non la riporto perché è abbastanza complicata, ma vi assicuro che la descrive in modo perfetto!
La faccenda è ancora più fantastica, in quanto questa equazione permette di ricavare le leggi empiriche di Wien e di Stefan-Boltzmann. Noi potremmo anche essere po’ sorpresi di quanto ottenuto, tuttavia, il più sorpreso di tutti è stato proprio Planck che pensava a tutto ciò come a un espediente matematico, ma non certo a una soluzione fisica e reale. Sì, sì, funzionava, ma la matematica aveva descritto qualcosa senza tener conto di come funzionava la fisica. Un bel gioco, ma niente di più. Senza nemmeno volerlo, Planck aveva dato il via alla meccanica quantistica!
Il primo a dimostrare quanto questa idea fosse concreta e non un semplice gioco di prestigio, è stato proprio colui che si è, in seguito, sempre opposto ai risvolti probabilistici della meccanica quantistica, Albert Einstein.
Il grande fisico è riuscito a spiegare, utilizzando i quanti di Planck, l’emissione di elettroni da una superficie metallica che viene colpita da un fascio di fotoni, ossia da una radiazione elettromagnetica. Einstein ha stabilito che l’emissione dipende fortemente dalla lunghezza d’onda della luce incidente e ha approfittato dell’ipotesi di Planck per fornire la soluzione rivoluzionaria.
L’energia incidente non è distribuita in modo uniforme, ma attraverso pacchetti di energia, i quanti di Planck, funzioni della frequenza. I fotoni possono quindi essere considerate vere e proprie particelle che trasmettono la loro energia (variabile a seconda della frequenza) agli elettroni che vengono colpiti. Se questa energia è sufficiente, gli elettroni vengono addirittura cacciati dall’atomo. La quantità minima di energia per riuscire in questo compito non è altro che quella descritta da Planck (ma che Einstein comunicò per primo). La conosciamo già:
E = hν
O, inserendo la lunghezza d’onda λ:
E = h(c/λ)
Dove c è la velocità della luce e h è, ovviamente, la costante di Planck.
In parole semplici, solo se il fotone è della giusta frequenza e ha la giusta energia può staccare un elettrone dal nucleo e renderlo… libero. Non solo. Se l’energia è superiore al valore limite, l’elettrone ne porta un po’ con sé sotto forma di energia cinetica e quindi può viaggiare facendo il suo slalom tra nuclei, atomi e molecole. Abbiamo descritto il celeberrimo effetto fotoelettrico.
Tutto sta tornando perfettamente con quanto descritto nelle pagine precedenti. Ogni materiale ha le sue regole, però. Infatti, l’energia di “liberazione” dipende molto dal tipo di atomo che trattiene i propri elettroni. Tutto ciò è fondamentale per creare il nuovo modello dell’atomo e descrivere la sua capacità di emettere o assorbire radiazione elettromagnetica. Come ovvia conseguenza, nascono le righe spettrali che variano da materiale a materiale e il cerchio si stringe sempre più. Un processo che la QED ci ha insegnato benissimo.
Questa scoperta ha dato a Einstein il Premio Nobel e ha aperto la strada, in modo dirompente, alla meccanica quantistica. Chi è stato lo studioso che ha cercato di lottare più duramente contro la spiegazione di Einstein. Sembra impossibile: proprio Planck, colui che aveva fornito l’idea di base ad Einstein, ma che non poteva credere che la fisica classica fosse da “rivoltare” fino a questo punto. La Scienza, a volte, può portare ad assurdità incomprensibili. Tuttavia, le grandi menti lavorano con indomito coraggio, ma anche con estrema attenzione al lavoro precedente. Ci vuole il giusto tempo per accettare visioni rivoluzionarie.
Stelle e atomi si abbracciano
Siamo arrivati a un punto fondamentale. Sappiamo come misurare la temperatura superficiale di una stella, paragonando il suo spettro continuo a quello di un corpo nero. Siamo, però, anche in grado di descrivere la struttura dell’atomo e le azioni che subisce sotto l’effetto dell’energia elettromagnetica (i fotoni con le loro lunghezze d’onda). Non sempre, infatti, i fotoni e i loro pacchetti d’energia riescono a “cacciare” gli elettroni dall’abbraccio del nucleo. A volte, possono solo spostarli da una posizione a un'altra, ma non certo in maniera qualsiasi!
Siamo anche giunti al punto chiave per capire quelle strane righe nere che “disturbano” gli spettri stellari. Altro che disturbo! Sono proprio loro, legate ai “salti” degli elettroni nei diversi atomi, a informarci sugli “abitanti” presenti nelle superfici stellari. La faccenda diventa sempre più affascinante. La luce è veramente una miniera di in formazioni!
Ribadiamo, ancora, un concetto rivoluzionario che ha cambiato l'aspetto dei fotoni o -ancora meglio- ha sanato l'ambiguità onda-particella. I fotoni sono vibrazioni del campo elettromagnetico e si propagano come onde. Tuttavia, ogni onda porta con sé un pacchetto di energia, che dipende dalla frequenza dell'onda. L'onda può quindi benissimo vedersi come un qualcosa di corpuscolare. D'altra parte Einstein ha dimostrato che queste onde sono in grado di colpire e spostare un elettrone. Resta solo da capire cosa siano realmente queste onde prima che si manifestino come pacchetti molto robusti. L'ultimo tassello è stato inserito dalla meccanica quantistica: le onde non sono vere onde "fisiche", ma onde di probabilità. Esse indicano solo dove il pacchetto fotone potrebbe trovarsi in un certo momento. Quando colpisce l'elettrone non c'è più bisogno di usarle dato che sappiamo dov'è il pacchetto, ma, prima, il pacchetto vagabondo può essere solo descritto da un'onda di probabilità. Insomma, qualcosa del genere... ma ovviamente la meccanica quantistica non si può riassumere in una frase. Noi, però, l'abbiamo già trattata in lungo e in largo e ormai non ci spaventa più di tanto.
L'atomo quasi quantistico
Consideriamo nuovamente il nostro scivolo e la nostra scala a gradini. Abbiamo visto che nel primo caso l’energia potenziale diminuisce in maniera continua a mano a mano che si scende verso il basso. Usando la scala, invece, ci si riesce a fermare a ogni gradino. Vediamo la faccenda in modo leggermente diverso.
Nel caso dello scivolo è possibile assumere tutte le possibili energie potenziali passando dal punto di partenza a quello di arrivo. Immaginiamo che ci si possa anche fermare per una frazione infinitesima di secondo in qualsiasi punto. Teoricamente lo potremmo fare, dato che siamo costretti a toccare ogni punto. Tuttavia, sarebbe una fermata “immaginaria”, in quanto saremmo subito trascinati verso il basso nella irrefrenabile caduta.
Nel caso della scala, invece, non possiamo fermarci dove vogliamo, dato che saltiamo da un gradino all’altro, ma quando siamo su uno di loro, possiamo riposarci e dare un’occhiata intorno senza alcuna paura. Nei punti predisposti, ossia sui gradini, la situazione è decisamente tranquilla e abbastanza stabile. Possiamo dirlo in modo più scientifico. I gradini rappresentano soluzioni stabili di energia potenziale, un’energia, ricordiamo, che dipende dall’altezza rispetto al suolo.
La situazione dello scivolo ci ricorda il modello atomico di Rutheford. In esso si ammetteva che gli elettroni fossero liberi di rivolvere attorno al nucleo su una qualsiasi orbita, in modo analogo a ciò che fanno i pianeti attorno al Sole. Tuttavia, le cose non potevano funzionare, in quanto un oggetto (l’elettrone) che descrive un moto circolare subisce una certa accelerazione centripeta (come descritto nel moto circolare uniforme). Inoltre, l’elettrone è anche una particella carica che deve seguire le leggi dell’elettromagnetismo ed esse impongono che, se una particella accelera, è costretta a emettere energia elettromagnetica (lo sappiamo già dal corpo nero).
L’energia non è un pozzo senza fondo: quando viene emessa, lo fa a scapito dell’altra energia che la particella possiede, ossia quella cinetica di rivoluzione attorno al nucleo. Essa deve, perciò, diminuire e portare l’elettrone su orbite sempre più vicine al nucleo fino a cadere su di esso. Questo, ovviamente, non può capitare in Natura! E se anche capitasse, vorrebbe dire che durante la caduta l’elettrone dovrebbe emettere energia elettromagnetica su tutte le lunghezze d’onda. Insomma, dovrebbe dar luogo a uno spettro continuo. E anche questo fenomeno non si osserva assolutamente.
Ricapitolando, l’atomo di Rutherford è stato sicuramente geniale nell’ipotizzare gli elettroni posti in orbita attorno al nucleo a una certa distanza, ma ha bisogno di una scala a gradini, invece che di uno scivolo. In altre parole, gli elettroni possono trovarsi su orbite molto particolari e non ovunque. Sui gradini, ossia su orbite che sono stabili, possono “riposarsi” e non emettere energia elettromagnetica. Se non la emettono, possono conservare tranquillamente anche quella cinetica che li fa ruotare in modo costante e duraturo attorno al nucleo.
Gli elettroni non sanno stare fermi su un solo gradino
Condizioni magnifiche che, però, darebbero all’atomo una struttura fin troppo immobile e statica. Sappiamo benissimo che gli atomi e, a maggior ragione, gli elettroni che ne rappresentano le parti più esterne e vulnerabili, sono continuamente urtati da fotoni, ossia energia elettromagnetica, come abbiamo ampiamente descritto nelle pagine precedenti. In altre parole, i gradini sono terrazze panoramiche stabili, ma non senza rischi. Abbiamo già visto che se arriva un fotone molto energetico, esso è anche capace di fare schizzare l’elettrone fuori dall’atomo (ce lo ha dimostrato l’effetto fotoelettrico di Einstein) e cominciare a emettere su varie lunghezze d’onda a seconda della traiettoria e degli incontri che farà. Insomma, l’atomo viene ionizzato. Condizioni perfette per ottenere uno spettro continuo.
Anche senza arrivare a questi limiti, però, basta che il fotone incidente sia abbastanza energetico da costringerlo a salire su uno scalino più alto. Più in alto, ovviamente, dato che acquista energia. Un regalo insperato, ma di brevissima durata. L’energia regalatagli in questo modo viene subito restituita, emettendo un nuovo fotone che ha la stessa energia fornitagli poco prima. L’elettrone, insomma, può permettersi di saltare da un gradino a uno superiore, ma poi deve ripiombare in quello originario, come mostrato in modo “allegorico” nella Fig. 21. I vari gradini sono le uniche orbite stabili in cui possono rimanere gli elettroni, senza emettere energia. Sono anche ammessi salti multipli, come vedremo tra non molto.
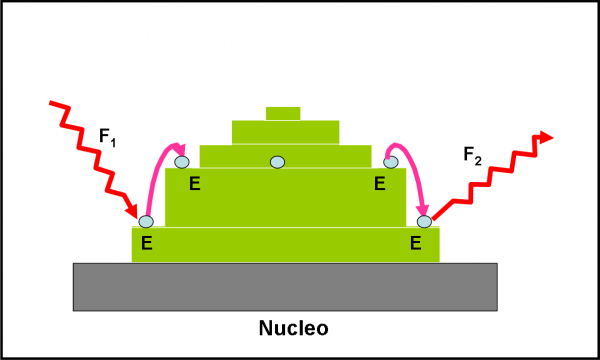
Su queste considerazioni, molto semplificate, si base il modello atomico di Bohr, che funziona perfettamente bene sull’atomo più semplice che esiste in Natura, quello di idrogeno, dato che possiede un solo elettrone. Vediamo di approfondirlo adeguatamente, scrivendo anche qualche semplice formula.
Due sono stati gli spunti che hanno portato Bohr a modificare velocemente l’atomo di Rutherford. Innanzitutto, la presenza delle righe spettrali, quelle righe nere che “disturbano” gli spettri stellari, ma che compaiono luminose quando si riscalda un gas rarefatto, e la nuova visione dell’energia che viaggia a pacchetti, formulata quasi per scherzo da Planck e confermata da Einstein.
I salti degli elettroni lasciano il segno
Il risultato finale è quello di un atomo in cui gli elettroni girano sì attorno al nucleo, ma solo e soltanto su orbite particolari, dove non possono emettere radiazioni e quindi perdere energia. Per emettere radiazioni devono essere eccitati, ma non in modo qualsiasi, bensì ricevendo un’energia sufficiente per farli passare da una orbita stabile a un’altra più alta (più energetica) per poi tornare immediatamente indietro. In quest’ultimo salto si rilascia l’energia ricevuta e si forma la riga luminosa (o scura) dello spettro elettromagnetico. La frequenza relativa al salto effettuato è ben determinato e quindi l’emissione è ben rintracciabile nel diagramma luminosità-frequenza (o lunghezza d’onda).
Insomma, quelle righe non sono altro che segnali chiari e precisi di quali salti fanno gli elettroni di un certo atomo. Essi emettono energia e brillano se non vi è uno spettro continuo a fare da sfondo, oppure appaiono come righe nere se si sovrappongono allo spettro continuo più luminoso di loro (ma vedremo meglio questa differenza).
Il lavoro mentale e deduttivo di Bohr si esprime sotto forma di due postulati che rappresentano l’ultimo tentativo di legare in qualche modo la fisica classica con l’emergente meccanica quantistica. Da allora in poi, il microcosmo si è completamente immerso nella seconda, l’unica in grado di descriverlo.
Primo postulato: l'elettrone può percorrere attorno al nucleo solo alcune orbite circolari senza perdere energia
In parole matematiche: il momento angolare dell’elettrone, su queste orbite, è una costante che altri non è che la costante di Planck divisa per 2π. La costante è moltiplicata per un numero intero che va da 1 in su (teoricamente fino a infinito) e che identifica tutte le orbite stabili. La formula che definisce quanto appena detto è:
L= mvr = nh/2π
Dove L è il momento angolare (ossia la quantità di moto mv moltiplicata per il raggio r dell’orbita). n è un numero che assume teoricamente tutti i valori interi. Espressa in altre parole, la relazione dice che la quantità di moto dell’elettrone moltiplicata per lunghezza della circonferenza percorsa è uguale alla costante di Planck moltiplicata per il numero intero.
Il numero n è stato chiamato da Bohr numero quantico ed è quello che permette di definire l’orbita in cui si trova l’elettrone.
Questa condizione implica che il momento angolare dell'elettrone non può assumere tutti i valori possibili, ma soltanto alcuni. Imporre questa limitazione significa quantizzare il momento angolare. Questo può variare perciò solo per “quanti”, multipli interi del valore minimo (h/2π), relativo a n = 1.
Secondo postulato: l'energia assorbita da un elettrone ne consente la transizione dall'orbita in cui si trova normalmente (stato fondamentale), a una delle orbite di energia quantizzata superiore (stato eccitato).
In queste orbite, l'elettrone permane per un tempo brevissimo (10-9 sec), per poi ritornare allo stato energetico fondamentale. Questo salto è quello che gli permette di liberare l’energia assorbita senza decadere verso il nucleo (“scala” e non “scivolo”) e di emettere secondo una ben definita frequenza. Un atomo allo stato eccitato può tornare allo stato fondamentale emettendo un fotone la cui energia è uguale alla differenza tra quelle dei due stati tra cui avviene il salto. In parole matematiche:
E2 - E1 = ν h
Essa non è altro che la formula pensata da Planck e divulgata da Einstein… ricordate?
Quantizziamo tutto!
Il modello di Bohr, ancora legato a una visione classica, riesce a descrivere molto bene l’atomo più semplice, quello in cui vi è un solo elettrone e un solo protone (idrogeno). In queste condizioni si può applicare il secondo principio della dinamica (F = ma) all’elettrone di carica unitaria e e di massa m, considerando come forza quella coloumbiana fra nucleo positivo ed elettrone negativo (di pari carica). Ricordando che nel moto circolare uniforme a = v2/r, con banali passaggi matematici si arriva a una formula molto importante:
r = n2h2/4π2me2 = n2 r1
espressione nella quale non compare più la velocità dell'elettrone e che mostra come risultino quantizzati anche i raggi delle orbite dell'elettrone dell'atomo di idrogeno corrispondenti ai possibili stati stazionari. Infatti, tutte le grandezze che compaiono sono delle costanti, tranne il numero n.
Inserendo i valori corrispondenti alle varie grandezze in gioco, si ottengono i raggi di tutte le orbite ammesse per l’elettrone dell’atomo di idrogeno, utilizzando come unità di distanza il nanometro (nm, pari a un milionesimo di millimetro):
n = 1 r1 = 0.053 nm
n = 2 r2 = 22 0.053 = 0.212 nm
n = 3 r3 = 32 0.053 = 0.477 nm
…
Teoricamente un atomo “finisce” quando n va all’infinito. In modo analogo a ciò che fa l’attrazione gravitazionale. Tuttavia, per certi valori l’elettrone è praticamente libero e subisce le interazioni con gli altri atomi. Non solo, però... Nessun atomo può occupare orbite che superano un certo valore di n. Ne risulta che, in pratica, ogni atomo ha una sua energia di ionizzazione, ossia tale da farlo scappare dall'attrazione del nucleo. Per arrivare a questi calcoli bisogna, però, fare molta più strada... Teniamo, infine, conto che la posizione di un elettrone ha una sua probabilità di essere ottenuta (come ci dice la meccanica quantistica) e quindi un elettrone si trova con altissima probabilità solo molto vicino al suo nucleo. Insomma, non fatevi spaventare da numeri che portano a raggi infiniti e a energia nulle...
Trafficando con le solite relazioni si può anche scrivere l’espressione che descrive l’energia relativa a ogni orbita ammessa. In altre parole, si vede che anche l’energia è quantizzata secondo la formula:
E = -2π2me4/n2h2 = E1/n2
Variando n (l’unica variabile) si ottengono i valori delle diverse energie. Non fatevi ingannare dal fatto che al crescere di n l’energia sembra diminuire. Ricordatevi che c’è il segno meno davanti. Un valore negativo di un numero sempre più piccolo aumenta il proprio valore che si avvicina sempre più allo zero. Un po’ come nell’energia potenziale dovuta alla gravità. Più si va lontano dalla massa centrale, e maggiore è l’energia potenziale che, essendo negativa, tende a zero (valore massimo) per una distanza infinita. Per valori crescenti di n, però, l’energia cresce sempre di meno (ossia i gradini superiori si raggiungono con poca energia in più) e quindi non è difficile far saltare l’elettrone fuori dall’atomo se ne assorbe troppa (effetto fotoelettrico).
Per energia che tende a zero, si ottiene il fenomeno della ionizzazione, che ormai conosciamo molto bene e l’atomo è libero di viaggiare da solo.
Da quanto detto, il succo dell’atomo di Bohr è piuttosto semplice. Poiché l'elettrone dell'atomo di idrogeno può possedere soltanto i valori di energia definiti dalla precedente equazione, se si fornisce energia all'elettrone che si trova ad esempio sullo stato stazionario caratterizzato da n = 1, essa potrà essere assorbita dall'elettrone solo se è sufficiente a farlo saltare dal primo stato stazionario a uno successivo. Se non si ha la giusta forza è inutile provare a saltare sul gradino più alto!
L'elettrone eccitato tende poi a tornare spontaneamente nello stato di minore energia (n=1) riemettendo di nuovo, sotto forma di radiazione, l'energia che ha assorbito.
Facciamo l’ultimo passetto e cerchiamo di determinare a quali frequenze l’atomo di idrogeno può emettere. In altra parole, cerchiamo le frequenza delle ormai celebri righe spettrali relative all’atomo di idrogeno, ossia le sue “impronte digitali”. Basta ricordare la solita formula di Planck-Einstein che lega energia e frequenza (la base della meccanica quantistica):
E = hν
Questa formula ci dice che una radiazione possiede una certa energia che va a pacchetti e non in modo continuo. Per ottenere un pacchetto di un certo valore si deve usare una ben determinata frequenza. Nota l’energia, quindi, è immediatamente nota anche la frequenza corrispondente. In poche parole, per fornire all'elettrone energia è necessario servirsi di una radiazione di frequenza opportuna.
Nel passaggio dell'elettrone dell'atomo di idrogeno da uno stato eccitato, con numero quantico n2 ed energia E2 ad uno stato di minore energia con numero quantico n1 < n2 ed energia E1 < E2, si ha un’emissione di energia sotto forma di radiazione con frequenza che si scrive:
ν = (E2 – E1)/h
A questo punto basta, nuovamente, trafficare un po’ con le formula precedente, relativa all’energia, e si ottiene:
ν = (E2 – E1)/h = (2π2me4/h3) (1/n12 – 1/n22)
che permette di calcolare tutte le frequenze che l'atomo di idrogeno eccitato può emettere tornando allo stato fondamentale (spettro di emissione) o assorbire eccitandosi (spettro di assorbimento), per ogni salto dell'elettrone fra due dei possibili stati stazionari di numeri quantici n1 e n2.
I principali limiti del modello di Bohr (già noti al tempo del modello) sono i seguenti: (a) non funziona per atomi a più elettroni; (b) non spiega i multipletti (righe osservate sperimentalmente molto vicine tra loro); (c) non dà indicazioni sull’intensità delle righe. Tutte cose che vedremo in seguito.
Prima di andare oltre e affrontare atomi più complicati, dove il modello di Bohr non riesce più a funzionare, vediamo dettagliatamente cosa succede esattamente al nostro semplice, ma fondamentale, idrogeno.
Basta disegnare un semplice diagramma, in cui sono rappresentate come linee orizzontali i vari livelli energetici delle orbite dell’elettrone. I balzi da una linea a un'altra causano differenze di energia e quindi differenti frequenze. Queste frequenze sono quelle relative alla righe dello spettro, come illustrato in Fig. 22.
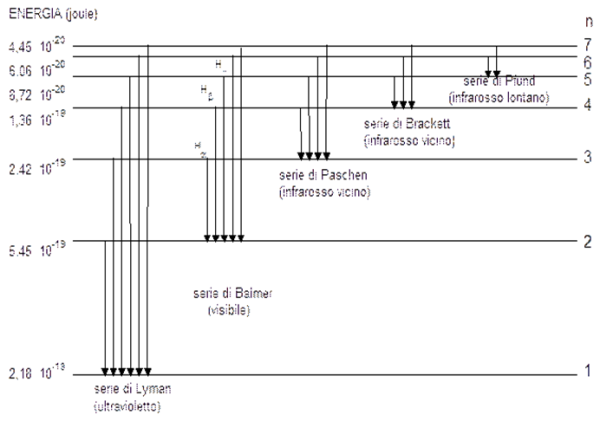
Volendo si può anche mostrare la situazione attraverso le vere e proprie orbite possibili degli elettroni (Fig. 23)
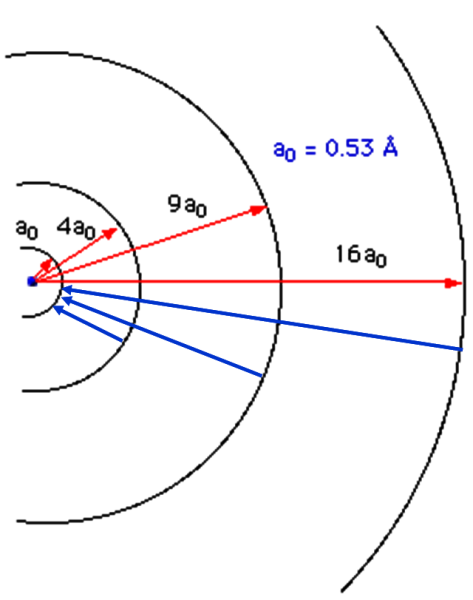
Righe chiare e righe scure
Se il salto assorbe energia (l’elettrone riceve energia) le righe appaiono scure nello spettro continuo. Perché? Perché l’atomo elimina dallo spettro di sfondo proprio l’energia relativa alle frequenze usate per far saltare gli elettroni. Quando poi l’elettrone torna al suo posto, l’energia è inviata in una direzione qualsiasi e non è assolutamente detto che arrivi all’osservatore (o quantomeno ne arriva solo una parte e quindi si abbassa l’intensità)
Se, invece, il salto è quello che riporta l’elettrone nelle condizioni originarie, si ha emissione di energia (righe luminose in assenza di spettro continuo). Si ha questa situazione, quando si eccita termicamente un gas rarefatto. La luce che si ottiene è solo quella emessa nei salti degli elettroni che tornano nel gradino di base. Non compare nessuno spettro continuo e si vedono solo le righe, relative ai salti che inviano la luce proprio verso l’osservatore.
Introduciamo la Fig. 24 per fare ancora maggiore chiarezza.
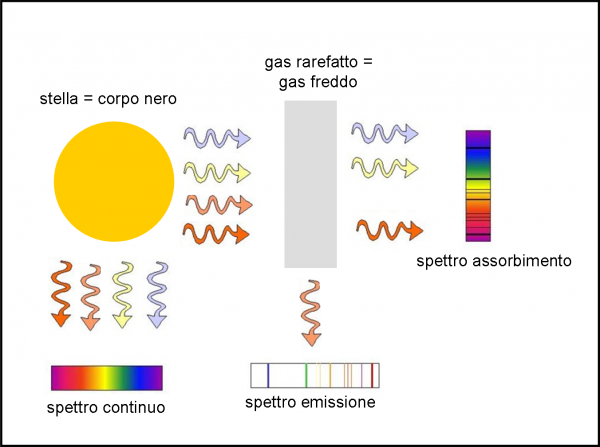
Una stella emette nel continuo come un corpo nero. Se assumiamo che essa sia esattamente un corpo nero riceviamo la luce in basso a sinistra. Se, invece, la luce della stella, prima di giungere a noi, deve attraversare del gas rarefatto e abbastanza freddo (atmosfera stellare, ad esempio), gli atomi di questo strato ricevono i fotoni della stella e quelli "giusti" fanno saltare gli elettroni solo da un livello a un altro (senza scacciarli del tutto). In altre parole, gli elettroni che saltano assorbono i fotoni di una certa lunghezza d'onda e non li fanno arrivare fino a noi (a destra in alto). E' vero che poi questi elettroni tornano a casa ed emettono fotoni, ma li possono mandare un po' ovunque e quelli che viaggiano proprio nella nostra direzione saranno ben pochi. In corrispondenza delle frequenze dei salti vediamo delle righe scure. Lo spettro è quello di assorbimento, in cui le righe si sovrappongono al continuo.
Se, però, siamo sistemati a novanta gradi (in basso a destra) rispetto a una nube di gas rarefatto che viene investita dalla luce di una stella, cosa succede? Beh..., di sicuro non vediamo lo spettro continuo della stella che attraversa la nube (bisognerebbe essere nella posizione di prima, in alto a destra). La nube, però, assorbe alcune frequenze e poi le rimette. Dato che le riemette in ogni direzione, qualche fotone riusce a raggiungere anche noi che siamo sistemati di lato. Ciò che vediamo sono, allora, solo le righe (luminose) che corrispondono ai fotoni emessi durante il salto degli elettroni. Abbiamo uno spettro di emissione.
Inseriamo anche la Fig. 25 per spiegare ancora meglio la differenza di come noi vediamo, a seconda della posizione, il lavoro fatto, nell'atomo del gas rarefatto investito dalla luce del continuo, dagli elettroni "salterini". In pratica, tutto dipende dalla nostra posizione... In un caso, l'atomo riduce la luce di una certa frequenza, rispetto a quella libera di arrivare fino a noi. Nell'altro, quel poco che ci manda è l'unica cosa che riusciamo a vedere. Meglio poco che niente!
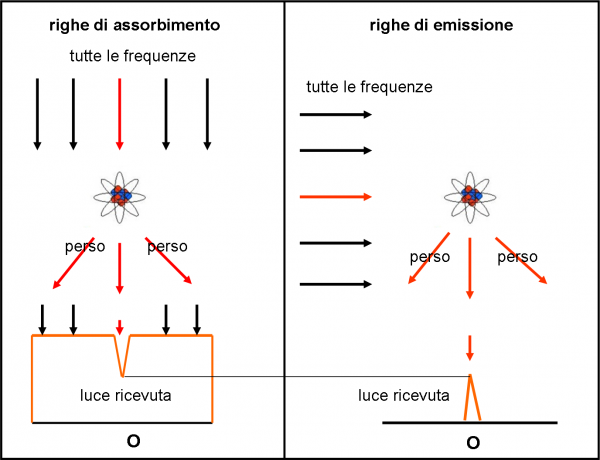
Le righe, proprio per come si ottengono, devono coincidere (uguale differenza di energia e quindi uguale frequenza).
Come e dove si sistemano queste righe? Le abbiamo già viste nella Fig. 22, ma è meglio ripetere ancora il concetto. Se l’elettrone inizia e termina il suo salto nell’orbita più bassa (più probabile e stabile, dato che ha la minima energia) abbiamo righe più energetiche (i salti sono più grandi). Se i salti avvengono tra righe più alte, le frequenze diventano sempre minori dato che le differenze di energia diminuiscono. Le righe si spostano, quindi, verso frequenze più basse (lunghezza d’onda maggiori).
I vari tipi di salti possibili e, quindi, di righe che “sporcano” lo spettro continuo si inseriscono in intervalli diversi di frequenze. Ricordiamo, infatti, che più i salti sono energetici e più le frequenze sono alte. Se l’orbita di partenza e di arrivo è quella più bassa di tutte troviamo righe che cadono nell’ultravioletto. Se è la seconda o la terza o la quarta, le righe si spostano verso lunghezze d’onda maggiori (frequenze minori). Ribadiamo ancora una volta, se ce ne fosse bisogno, che ad ogni orbita dell’elettrone corrisponde un certo numero di frequenze, dipendenti dall’orbita più alta raggiunta nel salto e dal livello raggiunto nel ritorno. Abbiamo così gruppi di righe relative a livelli finali diversi, i cui nomi sono riportati in Fig. 22. Ogni gruppo si sposta verso lunghezze d’onda più grandi.
Riassumendo: chi comanda la frequenza è soprattutto l'orbita stabile raggiunta alla fine, ma per ognuna di queste orbite finali vi sono varie righe che dipendono dall'orbita di partenza. Ad esempio, la righe di Lyman sono le più energetiche e cadono nell'ultravioletto, dato che l'orbita stabile finale è quella più bassa. Tuttavia, esse sono più di una, dato che l'energia dipende dall'orbita di partenza. Cambiando, poi, orbita finale, ci si sposta verso lunghezze d'onda maggiori (l'energia finale è comunque minore), ma di nuovo ci saranno più righe a causa delle diverse orbite di partenza.
Da quanto abbiamo visto nelle figure precedenti, se del gas di idrogeno si trova negli strati più esterni e più freddi di una stella, lo spettro deve presentare le righe relative al suo atomo (righe di assorbimento). Se, invece, il gas è illuminato “di fianco” (nebulosa ad emissione) vediamo solo le righe di emissione dell’idrogeno. Le righe, comunque, mantengono sempre la stessa posizione, ossia hanno sempre la stessa frequenza.
Non è difficile capire che la presenza di certe righe ben definite ci dice che è presente l’idrogeno.
Come volevasi dimostrare: le righe sono proprio la carta d’identità di un certo elemento. Senza parlare, poi, della loro intensità e di tante altre caratteristiche che migliorano sempre più l’informazione. Mamma mia, quante informazioni in quel simpatico fotone, un pacchetto veramente insostituibile!
Perché solo orbite circolari?
Niente da dire. L’atomo di Bohr è sicuramente rivoluzionario come concetto e fa uso delle recentissime scoperte sull’energia “impacchettata”. Tuttavia, come già accennato, rimane ancora legato alla meccanica classica. Infatti, gli elettroni sono particelle ben definite che non possono trovarsi ovunque ma solo su certe orbite e che, quindi, possono permettersi salti più o meno energetici tra un gradino e l’altro (orbite), ma devono rapidamente tornare indietro. Nel frattempo, però, la meccanica quantistica va rapidamente avanti con le sue regole sempre meno comprensibili e gli atomi degli elementi più pesanti presentano righe spettrali che non possono essere spiegate con il semplice modello di Bohr. In fondo, esso fa sì uso dei pacchetti d’energia, ma simula ancora perfettamente un sistema planetario, dove non tutte le orbite sono possibili, ma solo alcune. Più o meno quello che capita con i pianeti del Sistema Solare.
I pianeti, però, hanno orbite che non sono circolari... Si può ancora migliorare qualcosa.
Il primo passo verso qualcosa di più complicato lo propone Sommerfeld nel 1915, assumendo orbite ellittiche per gli elettroni. Un passo ancora disperato per non staccarsi dalle leggi di Keplero.
Infatti, il modello di Bohr riesce a spiegare abbastanza bene lo spettro di emissione dell'idrogeno e di qualche metallo alcalino come il sodio e il litio; per l'elio, però, già si osservavano delle righe formate da "multipletti", ovvero righe secondarie molto vicine tra loro. I salti quantici di Bohr non possono spiegarle. La differenza di frequenza tra le righe secondarie è molto piccola per cui è possibile che, ad esempio, tra lo stato fondamentale e lo stato eccitato n = 2 siano possibili diverse situazioni stabili secondarie, rilevabili dalle righe secondarie dello spettro.
Sommerfeld propone, allora, una teoria in cui si ipotizzano orbite ellittiche, che abbiano il semiasse uguale al raggio di Bohr. Anche questo sistema è quantizzato, per cui Sommerfeld definisce un secondo numero quantico, il numero quantico orbitale ( l ) che determina la "quantizzazione dell'eccentricità dell'ellisse " che l'elettrone può percorrere nei suoi stati stazionari. In altre parole, il numero quantico orbitale definisce la forma dell'orbita. La descrizione non è banalissima.
Nel primo livello, l'elettrone può percorrere solo un'orbita circolare e niente cambia rispetto all'atomo di Bohr. Nel secondo livello oltre all'orbita circolare, l'elettrone può anche percorrere un'orbita ellittica. Nel terzo livello l'elettrone può occupare, oltre all'orbita circolare, due orbite ellittiche aventi sempre assi maggiori uguali al diametro dell'orbita circolare, ma con diversa eccentricità e cosi via. In altre parole, ad ogni livello n stabilito dal numero quantico principale, si associano n-1 orbite ellittiche. Qualcosa come quella rappresentata nella Fig. 26.
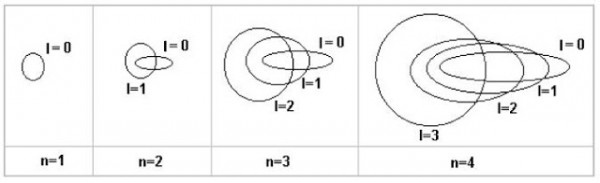
L'introduzione delle orbite ellittiche sembra rappresentare un' inutile complicazione nei calcoli. E, invece, riescono a spiegare la struttura fine delle righe spettrali. Sembrerebbe impossibile, dato che, in fondo, le orbite dovrebbero avere la stessa energia...
Bisogna tenere conto che la teoria di Bohr è una teoria non relativistica, nel senso che non utilizza le relazioni della relatività speciale. Esse possono essere trascurate solo se i corpi che si stanno studiando hanno velocità molto inferiori alla velocità della luce. L'elettrone è, però, proprio un qualcosa che ruota a velocità molto elevate e la relatività non può essere messa sotto al tappeto.
In pratica, nel moto lungo un'ellisse, l'elettrone è costretto a viaggiare più velocemente quando si trova più vicino al nucleo e più lentamente quando si trova più distante. La massa stessa subisce delle modificazioni, aumentando in prossimità del nucleo e diminuendo nel punto più distante. Ciò comporta una minima diversità delle energie associate alle orbite ellittiche, le quali non coincidono più con le energie delle orbite circolari dello stesso livello di Bohr.
Sommerfeld, insieme alla teoria della relatività, ha risolto, in parte, il problema!
Keplero non abita più qui...
Però, ormai, questo tipo di modello “kepleriano” si scontra sempre più con la meccanica quantistica e con i suoi principi, primo fra tutti quello di esclusione di Pauli. Al posto delle orbite subentrano gli orbitali, legati alla probabilità di un elettrone di stare in una certa regione attorno al nucleo. I numeri quantici si moltiplicano e piano piano si crea un'elegante e pressoché perfetta corrispondenza degli orbitali atomici con la Tavola Periodica degli elementi.
Anche se la spettroscopia sempre più fine non può evitare di risentire di queste continue migliorie, la faccenda si complica sempre di più. La struttura dell'atomo e tutti i suoi simpatici numeri quantici li vedremo in seguito. Fermiamoci a questo livello e ... usciamo a rivedere le stelle (e i loro spettri)!


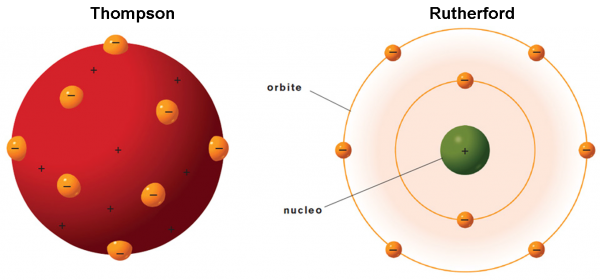




17 commenti
mamma enzo, un intero esame di università in una sola pagina di articolo

l'ho letto velocemente, devo dire la verità, mentre aspetto i medici però mi sembra che tu abbia detto tutto e anche di più
Beh... però è un articolo molto lungo...
volevo stamparlo e quindo ho scaricato in pdf. sono uscite 60 pagine

 e me lo farò rilegare per bene
e me lo farò rilegare per bene
dovrò andare in cartoleria
mamma mia
ne ho letto un terzo si e no,ci metterò una settimana se va bene
grandissimo enzo,impareggiabile
Ho aspettato un viaggio di 12 ore in aereo per gustarmi questo articolo...e tra snack, bicchieri di vino (orribili) e pisolini me lo sono finito...grande Enzo, articolo memorabile. Un gran bel ripasso, tante cose che non ricordavo e tante che non sapevo. Bellissimo.
Grazie Lampo e un abbraccio a tutti voi!!!!!
Grazie a te, Prof., per l'infinita disponibilità! , oggi conto di finire di leggere la QED e poi tirerò a sorte il prossimo argomento!
, oggi conto di finire di leggere la QED e poi tirerò a sorte il prossimo argomento!
Se marito e figlie mi lasciano tranquilla
Buona domenica a tutti!
cara Dany,
il mio è solo piacere e un sentito dovere di partecipazione! Comunque, prima la famiglia e poi tutto il resto!!!
D'accordo sul fatto che la famiglia sia più importante di tutto, ma qualche "briciola" di tempo per se stessi è doverosa!!

Mi piace troppo quando passo dopo passo ripercorri le tappe delle scoperte per arrivare a trattare l'argomento di turno certo è un lavoraccio ma secondo me paga.
Stavolta te lo meriti Bravo Enzo!
Super!!!
grazie Foscoul !!
che meraviglia di articolo, grazie mille Vincenzo!
ci sto mettendo parecchi giorni a leggerlo, ma il tuo modo di spiegare cose così complesse è talmente semplice che la lettura è assolutamente piacevole.
grazie Martino!
Articolo (sorry...LEZIONE ) SPETTACOLOSA ! me lo ero persone lontano 2011. Meno male che zampettando tra i tuoi (benedetti) QUI QUO QUA l'ho trovato. Ci passerò qualche ora interessante .
Grazie Enzo
P.S. Come mai da un po' di articoli è sparita la possibilità molto utile di fare Download PDF ? è vero che ormai si trova tale opzione sul browser ma spesso scarica un mare di link raffazzonati e non i disegni o le foto.
Caro Giorgio,
non ne sapevo niente... speriamo che Dany o Marco possano intervenire... HELP ME!!!!
Ho saputo da Marko che ha dovuto disattivare quel plugin perché è la probabile causa di alcuni problemi tecnici che si sono verificati recentemente nel blog. Non so se lo reinstallerà o lo sostituirà con un altro (questo ce li dirà lui).
Nel frattempo consiglio a chi vuole salvare gli articoli di copiaincollarli su word.
Per assistenza tecnica e/o consigli scrivete a papalscherzone@gmail.com (ma non spifferategli che ve l'ho dato io il suo indirizzo mail!)
Gran bel riassunto caro Enzone, come vedi tutto il tuo lavoro non va mai sprecato: l'hai scritto nel 2015 e io l'ho letto 8,7 anni dopo. Ora trasferisco anche il pdf nel mio e-book