Categorie: Fisica classica Matematica
Tags: accelerazione forza inerzia massa principi della dinamica relatività galileiana spostamento velocità vettore
Scritto da: Vincenzo Zappalà
Commenti:17
Esiste la forza centrifuga? (prima parte) **
Introduzione
Questo articolo è la risposta al “domandone” di qualche giorno fa. Alcuni sono stati abbastanza precisi nelle risposte, altri, invece, hanno mostrato una certa confusione nell’interpretare la forza centrifuga. Devo ammettere che non è colpa loro. La forza centrifuga ha messo in crisi molti professori e gli studenti ne sono stati, ovviamente, influenzati. Non parliamo, poi, di quello che si legge nella rete… Direi che è giunta l’ora di fare chiarezza una volta per tutte.
Posso già anticipare che la confusione nasce da un’errata applicazione del terzo principio della dinamica: ad ogni azione corrisponde una reazione uguale e contraria.
Inoltre, non si pensa mai abbastanza al sistema di riferimento in cui si descrive il moto. Ciò che sembra perfetto e stabile in uno è invece “disturbato” e anomalo in un altro.
Per comprendere questo problema basterebbe pensare alla relatività, ma non a quella di Einstein, bensì a quella perfettamente descritta da Galileo Galilei. Se un sistema di riferimento si muove rispetto a un altro di moto rettilineo uniforme, le leggi della meccanica possono essere spiegate esattamente nello stesso modo in entrambi i sistemi. Ciò vuole dire che non posso assolutamente capire se un osservatore è fermo o è in moto rettilineo uniforme.
Se, però, uno dei due sistemi non si muove di moto rettilineo uniforme rispetto a un altro, le cose cambiano. Dato che il fenomeno fisico che sta avvenendo non può essere diverso nei due casi, esso deve venire spiegato in modo diverso se riferito a uno o all’altro dei due sistemi. La spiegazione è relativa al sistemo di riferimento. Spero di avervi fatto venire l’acquolina in bocca… e allora iniziamo il nostro “giallo”.
Il movimento: una storia di malavita, di guardie del corpo, di sicari e di mandanti
Un breve antefatto è necessario per arrivare al problema di fondo. Il primo principio della dinamica dice che ogni corpo tende allo stato di quiete o di moto rettilineo uniforme se nessuna forza ESTERNA viene a disturbarlo. Esso è anche chiamato principio d’inerzia, in quanto implica che un corpo è soggetto a una specie di “forza” d’inerzia che lo obbliga o -ancora meglio- lo aiuta a mantenere un moto rettilineo e uniforme. Uniforme vuol dire “a velocità costante”, per cui è compreso anche il caso di quiete assoluta, in cui la velocità vale zero.
Sappiamo, però, molto bene che non vi è niente di veramente fermo nell’Universo e, quindi, che qualsiasi corpo, che non sia soggetto a forze agenti su di esso, resta in balia dell’inerzia e si muove a velocità costante. In realtà, l’inerzia non è una vera forza, ma una proprietà della materia e viene normalmente quantificata con la massa. Essa ha il compito di opporsi a qualsiasi azione di disturbo e difendere la tranquillità del corpo. Possiamo immaginarci l’inerzia come una vera guardia del … corpo, che non si nota quando tutto va bene, ma che entra in azione in caso di pericolo. Reagisce in modo simile a una forza solo e soltanto quando il corpo è soggetto a un’altra forza. Non agisce assolutamente se il corpo è in movimento rettilineo con velocità costante. Il nostro “personaggio” vive una vita perfetta e regolare grazie alla sua inerzia.
Tutti i sistemi di riferimento che permettono di descrivere questo movimento, per un corpo libero da forze esterne, sono detti inerziali. E’ facile intuire che i sistemi di riferimento inerziali sono tutti quelli che si muovono uno rispetto all’altro di moto rettilineo uniforme. In altre parole, in un sistema di riferimento inerziale qualsiasi, il corpo, soggetto solo alla sua inerzia, si vede sempre muovere di moto rettilineo e uniforme, ossia segue il primo principio della dinamica.
E’ facile intuire che è sempre possibile sceglierne uno rispetto al quale il corpo risulti immobile. Ciò che si muove di moto rettilineo uniforme in un sistema, può essere considerato fermo in un altro. Nessun corpo può rendersi conto se è in movimento o è fermo, dato che le leggi della meccanica rimangono perfettamente uguali. Questa constatazione, che chiunque può provare da solo, è la base della relatività galileiana. Se versate dell’acqua in un bicchiere ci riuscite sia se siete fermi in una stazione, sia se siete sopra un treno che viaggia velocissimo ma con moto rettilineo uniforme (nessuna brusca frenata o accelerazione e nemmeno una curva).
Ho detto forse cose ovvie, ma fondamentali per tutta la fisica da Galileo in poi. La relatività galileiana dice praticamente che le leggi della meccanica rimangono immutate in qualsiasi sistema inerziale o -se preferite- possono essere descritte in modo perfettamente identico. E’ lo stesso postulato usato da Einstein nella sua teoria della relatività. Egli accetta completamente il postulato di Galileo e ne aggiunge solo un altro che dice che la velocità della luce nel vuoto rimane sempre la stessa in qualsiasi sistema di riferimento. Una sola frase in più e tutto è stato cambiato e stravolto. Tuttavia, questa semplice verità ci deve far comprendere che il valore e i risultati della meccanica classica rimangono invariati se non ci avviciniamo a fenomeni che prevedono velocità simili a quella della luce.
Prima di procedere, è veramente fondamentale aver capito cosa s’intende per sistema inerziale. Se vi rimane qualche dubbio, fatelo subito presente e cercherò di eliminarlo fin dall’inizio.
La vittima innocente
Un corpo qualsiasi è quindi soggetto a una velocità, il cui valore dipende dal sistema di riferimento inerziale che è stato scelto per descriverlo. Passando da uno ad un altro, le leggi della meccanica devono rimanere le stesse. Scusate se ripeto ancora questo concetto, ma è alla base della “strana” caratteristica della forza centrifuga.
E’ solo e soltanto la velocità che caratterizza il movimento di un corpo. Anche se non ve ne sarebbe bisogno, ricordiamo, infatti, che la velocità è data dallo spostamento del corpo rispetto al tempo. E’, quindi, lei che determina il movimento. Senza di lei non ci sarebbe movimento. Se non intervengono forze esterne, la velocità resta costante. La massa (la guardia del corpo) cerca di aiutare il corpo a mantenerla in questo stato. Un corpo in movimento rettilineo uniforme è un personaggio tranquillo e inoffensivo, sempre che rimanga abbastanza isolato. Possiamo considerarlo come una vittima innocente.
Purtroppo, la massa, per attenta e preparata che sia, non riesce a controbattere azioni di disturbo esterne. Se questo succede, la prima cosa che varia è proprio la velocità del corpo e, come conseguenza, il suo movimento. Una grandezza meravigliosa (ma poco richiamata) che lega perfettamente la velocità e la sua guardia del corpo (massa) è la quantità di moto. Nient’altro che il prodotto tra velocità e massa. Un qualcosa che rimane anch’essa sempre uguale a se stessa fintanto che niente viene a disturbare il corpo in movimento. Una coppia veramente affiatata, dato che la sua costanza impone una legge fisica fondamentale: la conservazione della quantità di moto. Peccato non conoscerla meglio, ma dobbiamo proseguire nel nostro cammino giocoforza molto semplificato e abbreviato.
Vista l’importanza della velocità, conviene, però, definirla per bene, introducendo un vettore che la rappresenti. Un vettore è caratterizzato da un certo valore numerico (modulo) che ne definisce l’intensità. La lunghezza del vettore rappresenta quantitativamente il modulo. Il vettore ha anche una direzione, che identifica la direzione del moto. Se esso è rettilineo la direzione del vettore è quello della retta lungo cui si svolge il moto. Se, invece, la traiettoria descritta è una curva, la direzione della velocità istantanea è, in ogni punto, la tangente alla curva (ecco perché ho dovuto aspettare la derivata e il suo significato geometrico). L’ultima caratteristica del vettore è il verso che indica se il moto avviene verso valori positivi o negativi, rispetto al sistema di riferimento che si sta utilizzando. Il verso può essere “inglobato” nel modulo, facendogli assumere valori positivi o negativi a seconda del verso del moto.
Da quanto abbiamo detto e da quanto avete già imparato dai primi due capitoli della derivata, possiamo tranquillamente dire che la velocità istantanea del corpo, in un certo punto P, non è altro che la derivata dello spostamento del corpo rispetto al tempo e possiamo scrivere:
v = ds/dt …. (1)
dove ds e dt sono intervalli piccolissimi che tendono a zero.
Notale che ho scritto v e ds in grassetto, dato che rappresentano vettori, mentre dt è uno scalare, ossia un numero (d’altra parte la direzione del tempo è una e una soltanto e anche il suo verso). La derivata vettoriale contiene tutte le informazioni, ma non è eseguibile matematicamente in modo diretto. Conviene allora separare il modulo ds del vettore ds dalla direzione e scrivere:
v = ds/dt …. (1bis)
In questo modo ricavo il modulo v della velocità v. Spesso, i vettori sono anche indicati con una freccetta sopra la lettera. Questo comporta problemi nella scrittura del testo e, allora, utilizzo il metodo del “grassetto”. In articoli precedenti non avevo tenuto conto di questa possibilità, dato che non parlavamo di vettori. Adesso, però, starò molto attento e quando vedrete una lettera scritta in grassetto saprete che rappresenta un vettore.
Vale la pena fare una piccola, ma importantissima, riflessione per eliminare possibili confusioni. Se il moto del corpo descrive una curva y = f(x), la derivata f ’(x), calcolata nel punto P occupato dal corpo, identifica il coefficiente angolare della retta tangente al curva. In altre parole, determina la direzione del vettore velocità. La derivata dello spostamento lungo la curva rispetto al tempo determina, invece, il modulo della velocità, ossia quanto è lungo il vettore. Stiamo bene attenti a non confondere le due cose.
Nel caso del moto rettilineo uniforme, la direzione della tangente alla “curva” è la retta stessa, mentre il valore della velocità si determina dalla variazione della distanza (misurata lungo la retta) divisa per l’intervallo di tempo. Essa risulta una costante, ovviamente, ma niente ha, comunque, a che vedere con la traiettoria della retta in cui avviene il moto. La stessa velocità (in modulo), infatti, si può ottenere su qualsiasi retta. Il modulo della velocità resta costante, ma cambia la direzione. Una cosa analoga, anche se leggermente più complicata, si ha per una traiettoria curva.
Riflettete bene su questo punto, perché non deve assolutamente portarvi a confusioni “deleterie”. Riassumendo ancora: la derivata, rispetto al tempo, dello spazio percorso lungo la traiettoria determina il modulo della velocità; la derivata, rispetto a x, della funzione traiettoria espressa come y = f(x), determina il coefficiente angolare della retta (tangente) che ha la direzione della velocità. Mi raccomando… capite bene questa differenza.
Il sicario prezzolato
Sembrerebbe, da quanto detto, che anche su una curva qualsiasi si può avere una velocità di modulo costante. Questo è sicuramente vero, ma non basta per soddisfare il principio d’inerzia che voleva un moto rettilineo e non solo uniforme. Ciò vuol dire che qualsiasi corpo si trovi a descrivere una traiettoria che non sia rettilinea deve sicuramente essere soggetto a un disturbo esterno. I vettori velocità, punto per punto, mantengono -magari- lo stesso modulo, ma cambiano direzione e quindi sono diversi. In modo analogo, anche se il corpo descrive una retta non è detto che accontenti il principio d’inerzia. Infatti, la velocità ha sempre la stessa direzione, ma potrebbe variare il proprio modulo. Il moto sarebbe rettilineo ma non uniforme. Niente da fare, l’inerzia, ossia la massa, non si accontenta di mezzo bicchiere, lo vuole sempre intero!
In un modo o nell’altro, sia che la velocità non rimanga costante in modulo, sia che cambi la direzione, il principio d’inerzia non è verificato e quindi sul corpo DEVE agire qualcosa di fastidioso e pericoloso.
Qual è la grandezza che caratterizza la variazione della velocità istantanea, ossia che impone una variazione al moto rettilineo uniforme? Essa prende il nome di accelerazione istantanea e non è altro che la variazione della velocità rispetto al tempo, nel punto P, ossia è la derivata della velocità rispetto al tempo, calcolata in P. Si può quindi scrivere:
a = dv/dt …. (2)
Il calcolo del modulo di un’accelerazione è meno semplice del previsto e passa attraverso la scomposizione del vettore lungo due direzioni particolari e perpendicolari tra di loro: una tangenziale (quella che aumenta o diminuisce il modulo della velocità lungo la tangente) e una normale (quella che varia la direzione del moto ed è diretta verso il centro del raggio di curvatura istantaneo). Dato che il nostro problema di fondo è un caso particolare, evitiamo la trattazione completa e le formule relative. Resta, comunque, il fatto che, nel caso più generale possibile, l’accelerazione si fa proprio in due per disturbare il primo principio della dinamica.
Prima di proseguire, ribadiamo un concetto molto importante. L’accelerazione non fa realmente muovere un corpo, ma fa solo variare la velocità. E’ la velocità -e solo la velocità- l’unica che riesce in questo compito (la massa risponde solo a lei… come un cane ben addestrato). Quando si dice che un corpo subisce un’accelerazione e quindi si muove è, in realtà un piccolo errore. Si dovrebbe dire che la velocità del corpo subisce una variazione dovuta all’accelerazione. Un corpo che cade per terra ha una certa velocità iniziale, magari proprio zero. Tuttavia, essa è soggetta all’accelerazione di gravità (che possiamo considerare una costante vicino alla Terra) e quindi è costretta a variare il proprio modulo in modo crescente (moto rettilineo UNIFORMEMETE accelerato, dato che l’accelerazione è costante). L’accelerazione causa un aumento nella velocità, ma è sempre lei e soltanto lei che dirige il movimento, portandosi dietro la guardia del corpo massa. Anzi, nel caso della caduta dovuta alla gravità, la massa non ha nessuna importanza e non riesce a rispondere “apparentemente” in alcun modo. Subisce e basta. Ho appena enunciato il concetto del tutto “contro intuitivo” della caduta dei gravi: una piuma o una palla di piombo cadono alla stessa velocità. State tranquilli che tra non molto risolveremo anche questo enigma…
Come si determina, nei casi più generali, la direzione dell’accelerazione? Non è cosa facilissima, ma viene in aiuto la regola della somma (e differenza) dei vettori. D’altra parte la relazione (2) indica proprio che l’accelerazione si determina facendo una differenza di vettori velocità (dv). Il fatto di dividere per un numero come dt può solo cambiare il modulo del vettore finale, ma non la sua direzione. Per sommare o sottrarre due vettori si usa la ben nota regola del parallelogramma. Prima di applicarla ricordiamo che il verso di un vettore è dato, in realtà, dal segno del suo modulo: se è positivo va in un certo verso, se è negativo nel verso opposto. Ne segue che per passare da un vettore v a uno –v basta invertire il verso, mantenendo uguale modulo e direzione. Usiamo la Fig. 1 per definire la regola.
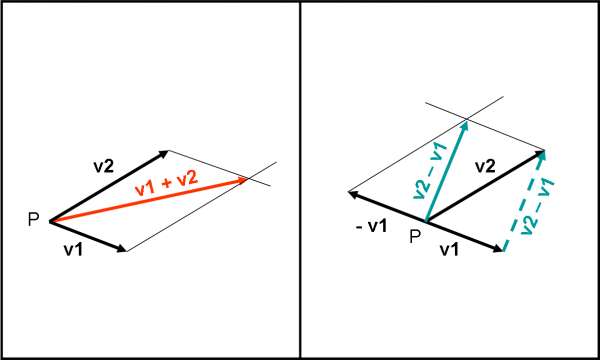
A sinistra, vediamo come si esegue la somma dei due vettori v1 e v2. Essa risulta uguale a una diagonale del parallelogramma; a destra vediamo come si esegue la differenza tra v2 e v1. Notate che in questo secondo caso non ho fatto altro che disegnare il vettore –v1 e sommarlo a v2. Risulta che il vettore differenza è l’altra diagonale del parallelogramma.
In Fig. 2, applichiamo quanto appena imparato al caso della velocità e dell’accelerazione. Immaginiamo che i punti P1 e P2 siano vicinissimi e che v2 non sia altro che v1 + dv (dv piccolo a piacere). La differenza vettoriale v2 – v1 e proprio uguale a dv e, di conseguenza, è la direzione dell’accelerazione.
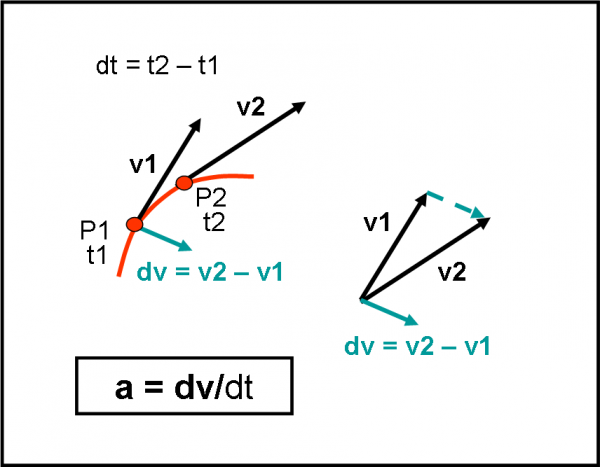
A questo punto basta trovare le componenti del vettore lungo due direzioni particolari (quella tangenziale e quella normale) per risolvere completamente la faccenda, come mostrato in Fig. 3. Vi informo che la componente normale si chiama anche accelerazione centripeta e questo nome la dice già lunga… Notiamo, inoltre, che ogni componente ha un suo ben preciso compito. Quella tangenziale modifica solo il modulo della velocità; quella centripeta modifica solo la direzione. Cose già dette, ma troppo importanti per rischiare di perderle per strada…
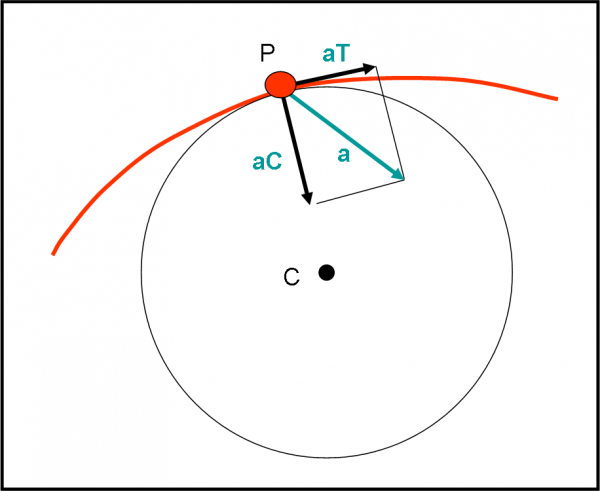
Avrete notato che ho inserito tranquillamente il cerchio osculatore, alla curva traiettoria, nel punto P. Ormai lo conosciamo bene, dato che è lui che ci permette di definire geometricamente la tangente a una curva senza mettere in ballo la derivata. Ovviamente, la componente centripeta è istante per istante diretta verso il suo centro, mentre la componente tangenziale è sempre, istante per istante, normale a questa direzione.
Un moto curvilineo qualsiasi lo possiamo anche immaginare come la traiettoria che ha in ogni suo punto la velocità come tangente, una specie di inviluppo delle velocità. La velocità non cambia per niente? E allora il moto è rettilineo e uniforme. La velocità cambia direzione? E allora la traiettoria è obbligata a curvare. La velocità cambia solo il modulo? E allora la traiettoria rimane una retta, ma viene percorsa più o meno velocemente. La velocità cambia solo direzione, ma non modulo? E allora la traiettoria è …. No, lo diremo tra poco, dato che è proprio il caso che c’interessa!
Possiamo definire l’accelerazione come una specie di sicario, che colpisce la velocità ma non influisce direttamente sul moto. Non si sporca le mani fino a quel punto. Comunque, essendo solo un sicario, pagato per colpire la vittima, è assai più importante trovare il mandante del crimine che ha infastidito al tal punto il moto rettilineo uniforme inerziale.
Alla ricerca del mandante
Riassumiamo in modo molto intuitivo. Un corpo si muoverebbe sempre secondo un moto rettilineo uniforme, ossia manterrebbe la sua velocità costante con la stessa direzione e verso. Se ci accorgiamo che il vettore velocità cambia, vuol dire che esiste qualcosa che lo disturba (lo devia o l'allunga o l'accorcia). L’unica cosa che può far variare la velocità è il “sicario” accelerazione. In particolare, se il movimento comincia a non essere rettilineo siamo più che sicuri che esiste un’accelerazione, dato che varia la direzione della velocità (è inutile controllare quanto vale il modulo). Se il moto resta rettilineo bisogna invece controllare se varia il modulo. Ribadiamo ancora che la presenza di un’accelerazione, ossia di un sicario, vuole dire, con la massima sicurezza, che esiste un mandante, ossia qualcosa che agisce sul corpo attraverso l’accelerazione. Il mandante prende nome di forza esterna. Come può agire il corpo per ribellarsi a questa imposizione esterna? L’unica sua arma è la massa (inerziale), ossia quel qualcosa che cerca di ridurre gli effetti del crimine. A parità di mandante, più la massa è grande è più è debole l’azione del sicario accelerazione. Con l’ultima frase abbiamo introdotto anche il secondo principio della dinamica… Torneremo, però, su quest’ultimo concetto, dato che, a volte, la massa gioca di … nascosto
C’è ancora da lavorare parecchio prima di arrivare sulla Luna. Ma abbiamo già incontrato parecchi personaggi veramente interessanti. Leggete e rileggete per essere pronti al passo finale.
Finiamo qui la prima parte del nostro piccolo giallo e … alla prossima puntata!






17 commenti
Ciao Enzo, questo va stampato e allegato alla Fisica Addormentata, è un bell'approfondimento visto che le derivate nel libro non sono contemplate (x fortuna eh! Meglio arrivarci con piccoli passi alle cose più difficili! :-D)
eh sì, carissimo... ne stiamo facendo di strada...!!!
Il signore in Giallo!!!
Enzo, sei impagabile, lo Ellery Queen della fisica!
Grazie per questi articoli, leggerti è una distrazione gratificante, tu sai quanto ne ho bisogno...
caro Beppe,
sono contentissimo di riuscire a lenire un po' i tuoi problemi...
un abbraccione!!!
Come sempre chiaro, bravo e preciso
E a questo punto io avrei una domanda, relativa alla forza centrifuga quando non è compensata dall'accelerazione gravitazionale di un corpo di massa ben maggiore attorno al quale noi, corpo di massa relativamente insignificante, si stia orbitando.
Premetto di essere ben consapevole di star per fare una figura decisamente barbina: ma c'è un caso in cui io la forza centrifuga non la "vedo" più come necessaria e scontata nella mia mente. O meglio... perdo le mie certezze relativamente alla sua entità, perché il sistema inerziale di riferimento mi diventa un po' metafisico, laddove quando stavo dalle mie parti (nel Sistema Solare, pieno di masse significative qui e là) tutto sembrava funzionare tanto bene.
Perché dico non compensata?
Perché ad esempio, se io rendo significativo e non trascurabile il rapporto fra le masse del corpo orbitante rispetto a quello attorno cui si orbita, ecco che devo ben tener conto del baricentro comune del sistema costituito dalle due masse (come se fossero unite da un segmento rigido ma di massa nulla), che trovo con una leva di primo genere: le metto su un perno che fa da altalena.
***
Nel caso della terra, il baricentro se non rammento male sarebbe sui 1800 km e qualcosa sotto la superficie della crosta, in media, per cui si può parlare ancora di sistema pianeta/satellite, e non di pianeta doppio. Ma ci son casi, come quello di certe stelle doppie, in cui il rapporto fra le masse è tanto vicino alla parità che esse appaiono ruotare all'opposizione l'una rispetto all'altra, attorno a un punto in cui non trovo masse di sorta. Perfetto. Vedo, vedo. Mi pare assolutamente necessario tutto ciò, forse vuol dire che l'ho un po' capito.
***
Quando la forza di attrazione gravitazionale non sia sufficiente, posso compensare la forza centrifuga con una reazione vincolare: è quello che tutti i bimbi sperimentano (anche il mio lo ha fatto, con prudenza che slogare la spalla di un bimbo è cosa da poco) quando papà o mamma gli fan fare "vola vola".
***
Ora, ancora una volta, il fulcro è il baricentro comune: anche un ex pilone della nazionale di Rugby da 160 kili mentre fa far "vola vola" al suo bimbo di 13 kili si inclina un po' all'indietro con l'asse delle gambe e la schiena, se no la forza centrifuga generata dalla rotazione dei due corpi lo sbilancerebbe in avanti. Evabbé.
***
Passiamo adesso ad una scala un po' più grande: la visionaria Stazione Spaziale di Wehrner Von Braun, quella "adottata" da Arthur Clarcke e omaggiata da Kubrik all'inizio di 2001 Odissea nello spazio. Alla Stazione, a forma di ruota di bicicletta, viene imposta una rotazione di velocità angolare calcolata accuratamente perché la forza centrifuga appaia agli occupanti come una gravità artificiale rivolta verso l'esterno, magari inferiore a quella terrestre sufficiente a non avviarli subito alle vertigini e presto all'osteoporosi ed altri acciacchi.
Anche nell'astronave verso Giove, mentre gli altri astronauti dormono felicemente ibernati, l'unico che resta sveglio a badare alla baracca fa jogging solo come un cane, accennando a qualche pugno all'aria come un pugile in allenamento, correndo in un interminabile (perché toroidale) corridoio in cui per lui il "pavimento" è la superficie esterna. Ricordi la scena? Per il 1967, un realismo incantevole.
Rispetto a che quella parte di astronave ruota attorno ad un asse? Rispetto ad un riferimento inerziale assoluto, come dici tu. Siamo nel Sistema solare, di massa in giro ce n'è tanta, siamo immersi in un campo gravitazionale variegato e potente. Fin qui, tutto bene.
***
Ma siamo arrivati al punto in cui il mio cervelletto bacato va in crisi.
Adesso io prendo la "ruota" di Von Braun, e grazie a dei potenti razzi vettori chimici all'inizio, a dei sofisticati e delicati propulsori a ioni poi, la accelero sino a fuggire al campo gravitazionale terrestre, ed anche ad allontanarsi seguendo una grande spirale dal Sole sino a sfuggire anche alla sua gravità, ed avventurarmi nello spazio interstellare.
Di più: siccome posso far funzionare il propulsore a ioni per un tempo molto lungo, piano piano piano ecco che esco dalla Via lattea, mi allontano dal gruppo locale di cui fa parte, mi allontano, mi allontano... verso una direzione nella quale trovo la massima scarsità di massa possibile.
Ora sono nel buio apparente più totale, se guardo fuori non vedo più non dico una stella che è una, ma nemmeno un debole evanescente fiocchetto indistinto che con un potente binocolo potrei identificare come una galassia o un ammasso. Nemmeno il telescopietto di bordo, con qualche decina di minuti di posa, mi fa vedere un accidente di niente.
Motori spenti. Ora accendo un pochino i propulsori tangenziali, quelli destinati ad imprimere un moto di rotazione alla ruota, come nel film. Li accendo con un impulso minimo, proprio minimo. La ruota inizia ad essere accelerata attorno al suo "mozzo", perché i motori sono in controfase. Proprio come si fa per generare una gravità artificiale.
Ora ogni punto della sua "circonferenza" (della ruota) e quindi anche io che sto dentro attendendo di poter fare jogging, viene perturbato dal suo stato di quiete o di moto rettilineo uniforme iniziale, e non c'è una accelerazione gravitazionale rivolta verso un centro di massa, perché la massa del centro rispetto a quella dei "bordi" non è poi dominante: quello che tiene insieme il tutto è la reazione vincolare, i "raggi della ruota" e la consistenza fisica della struttura.
Non c'è dubbio.
Ipotizziamo che SE potessi vederla dalla Terra, potrei osservare che da zero, gli ho pianiiiiiiiiiiiiiissimo fornito una velocità angolare di un giro ogni due secondi. Se fossi stato dalle parti del nostro mondo, due calcoletti e avrei potuto in base al diametro della faccenda dire "all'interno chi voglia far jogging vivrebbe una gravità artificiale di poco più di un terzo di quella terrestre, può andare".
Ma io mi son andato masochisticamente a ficcare in un punto dell'Universo che è straordinariamente in prima analisi vuoto, scarso di masse, son così misantropo e... misatro (se po' dì?) da non avere più la parvenza di un cielo stellato attorno. Il più lontano che posso da tutto. In un punto in cui se fossi stato messo là da una immensa manona divina, chissà quante decine di migliaia di anni ci vorrebbero perché un ipotetico supertelescopio a Terra potesse rilevare l'inizio della mia "caduta" verso qualcosa, la galassia o il gruppo di galassie più vicino, perché qualcosa ovviamente a grande distanza sempre c'è.
***
A questo punto, il sistema inerziale funziona esattamente come prima? Un giro ogni due sec attorno a un asse mi deve generare una "finta gravità" rivolta verso l'esterno (che altro non è che forza centrifuga che io vivo come gravità) uguale a quella che misurerei se fossi in orbita attorno a Urano? I numeri mi dicono di si, mi dicono "devi pensare a una terna cartesiana virtuale xyz che sta laggiù, pollice indice e medio a 90° fra di loro disegnate con le freccette e tutto quanto in bianco su fondo nero là nello spazio, tu non la vedi con gli occhi ma puoi mentalmente disegnarla, e rispetto alla quale se prima la ruota non ruotava, poi ruota, la forza centrifuga c'è, quindi conta la velocità angolare e la distanza dall'asse di rotazione esattamente come prima, le leggi dell'Universo non come le norme del Codice Penale per certi politici potenti quando finiscon nei guai, o valgono o non valgono, falla finita con questi distinguo" ma le budella questa cosa se sono in un punto molto molto isolato la accettano meno.
O meglio, non è che non la accettano, è che si perdono e cominciano a non "vederla". Perché è come se fosse la massa complessiva dell'Universo a determinare il sistema inerziale, il che è molto logico, l'Universo può dirmi come il marchese del Grillo "io so' io con le mie 10 alla chissàquanto t di materia totale e tu non sei un c..., perciò tutti i moti che ti prefiggi lineari o curvilinei o attorno a un asse sempre rispetto a me nel complesso li fai", però...
...però non lo vedo. Non ci arrivo proprio. La pancia mi dice che se non potrò mai essere fuori da qualsivoglia campo gravitazionale, perché se nell'Universo c'è materia dev'esserci un campo, però se vado scientemente a cercarmi un angolino molto molto vuoto, qualcosa dovrebbe agire meno. Come se quel giro ogni due sec, impostato all'inizio del viaggio, man mano che vado a cacciarmi in buie solitudini intergalattiche dovesse farmi registrare sulla bilancia un peso un cincischino inferiore, anche se nulla in assenza di attriti avrebbe potuto rallentarlo e quindi "so" che la velocità angolare è rimasta costante ...
Allora vuol dire che la mia pancia inizia a pensare a quel sistema inerziale di riferimento come un qualcosa di più evanescente, come se la nettezza del tratto grafica di quei tre assi xyz dipendesse dalla presenza di masse adeguatamente prossime che lo legittimino... come se un pochino, la legge quadratica inversa influenzasse anche l'autorevolezza del riferimento... il che NON ha logicamente senso!
Una donna non può essere "un po' incinta"!
Lo so che sbaglio, ma non capisco dove.
Perché con lo "vedo" più con la dovuta naturale evidenza, quando son lontano da tutto?
mamma mia, Valerio!
io cerco disperatamente di semplificare e non di complicare... Il tuo "romanzo" crea, invece, un insieme di situazioni particolari e generali mischiate assieme da diventare veramente incomprensibile. La fisica è semplice e deve essere spiegata in modo semplice. L'unica cosa che va imparata è che il modo con cui si spiega un fenomeno in un sistema inerziale non può più essere usato in un sistema non inerziale (ad, esempio rotante). Il fenomeno deve essere lo stesso, ma non il modo di spiegarlo. Che tu accendi un motore o ti metti in orbita attorno a una massa non cambia il succo del discorso. In entrambi i casi, se vedi la faccenda dall'esterno (sistema inerziale) esiste solo la forza centripeta, che sia la massa centrale o che sia il vincolo che non ti fa scappare per la tangente. Se invece ti metti nel sistema rotante, devi introdurre una forza centrifuga che viene annullata dalla forza centripeta affinché tu ti senta fermo. Non è il terzo principio della dinamica, stai attento! E' solo un annullamento di una forza che ti trascina e che tu devi annullare per stare fermo nel tuo sistema. Da fuori la forza che trascina non esiste, ma solo una velocità che tende a farti seguire un moto rettilineo uniforme che viene istante per istante piegata attraverso il sicario accelerazione che nasce dall'unica forza reale, ossia la centripeta. Per un satellite artificiale è la massa della Terra, per un razzo sono le pareti del razzo o la corda della giostra.
Non complichiamo inutilmente il discorso per renderlo più scientifico. Rimaniamo terra-terra: è più che sufficiente.
Inoltre, sono solo alla prima parte e non ho ancora introdotto nessuna forza... un po' di pazienza per coloro che seguono il discorso aspettando la soluzione del giallo
Prima di tutto buona Pasqua a tutti!
Poi, se questo può aiutare, rileggendo il post di Valerio mi sembra che l''incomprensione è generata dal fatto che mi pare confonda il calcolo dell'accelerazione di gravità con la forza centrifuga, soprattutto quando si rifà ad un sistema di riferimento gravitazionale con masse significativamente diverse,
cit : "Perché ad esempio, se io rendo significativo e non trascurabile il rapporto fra le masse del corpo orbitante rispetto a quello attorno cui si orbita, ecco che devo ben tener conto del baricentro comune del sistema costituito dalle due masse (come se fossero unite da un segmento rigido ma di massa nulla".
Mi fa pensare che si riferisca a questa formula:
o alla legge di gravitazione Universale,
ecco perché la sua idea di accelerazione vacilla se applicata in spazi privi da masse, come le chiama lui "di riferimento"
Nel nostro caso, correggetemi se sbaglio, la massa va intesa solamente come quantità di materia, e la forza centrifuga in un sistema di riferimento come ad esempio la nostra stazione spaziale rotante, dipendendo solo dalla velocità di rotazione è la medesima anche all'inferno!
Accidenti, non sono apparse le formule!
stiamo attenti ragazzi,
il fatto che le masse siano comparabili oppure no non cambia di certo la forza gravitazionale! Se voglio, posso sempre fare una trasformazione di assi e considerare un corpo immobile. Comunque sia, le masse si attraggono l'una con l'altra e ognuna di esse subisce l'accelerazione centripeta causata dalla forza gravitazionale e, nel sistema di riferimento rotante, anche la forza centrifuga. Che ruotino l'una attorno all'altra o attorno al baricentro non muta la situazione. La navicella spaziale ha bisogno di una velocità impartita da noi per potersi opporre all'accelerazione gravitazionale che tende a farla cadere e, quindi, si rimette in perfetta linea con un corpo naturale che ruota perché soggetto a una velocità rettilinea e uniforme deviata dall'accelerazione di gravità Se non ci sono masse in giro siamo nel caso della giostra con i seggiolini. Il motore impartisce una velocità rettilinea uniforme che viene contrastata dalla forza centripeta dovuta ai vincoli. Proprio come una macchina che fa una curva...
Su... aspettiamo di concludere il post prima di fare congetture. Se no si rischia di creare confusione su un argomento abbastanza spinoso.
caro Valerio,
ho cercato di leggere con attenzione il tuo post, eliminando tutte le parole di contorno che ravvivano lo scritto ma che creano confusione sul vero punto della questione. Sarebbe bello se riuscissi a scrivere in modo sintetico e descrivere il problema senza marchesi del grillo o cose del genere. Anche a me piace scherzare, ma per fare una domanda è necessario essere precisi e sintetici. Almeno io sono confuso da tanti voli della fantasia che non aiutano a entrare nel problema ma -sempre secondo me- a divagare e a disperdere l'attenzione. Oltretutto, ho anche settantanni...
Dunque le frasi che sembrano significative sono:
E a questo punto io avrei una domanda, relativa alla forza centrifuga quando non è compensata dall’accelerazione gravitazionale di un corpo di massa ben maggiore attorno al quale noi, corpo di massa relativamente insignificante, si stia orbitando.
Mi sembra, quindi che il problema sia relativo a quello di una giostra o di un'automonile che curva. Ossia, quando l'accelerazione centripeta (che è quella che fa variare la velocità) non è dovuta alla gravità, ma a qualche altra cosa.
OK?
Andiamo avanti:
il sistema inerziale di riferimento mi diventa un po’ metafisico
E qui già mi sembra che si cambi discorso. Perché metafisico? Se considero una giostra che gira, è facilissimo trovare un sistema che in prima approssimazione è inerziale. Basta sedersi su uno scalino e farsi trascinare solo dal moto della Terra e altre cose del genere. Rispetto al fenomeno che sto guardando, estremamente localizzato, è più che sufficiente stare fuori dalla giostra. Le perturbazioni dovute ai fenomeni vari dell'Universo possono essere completamente trascurate. Nessuno potrà mai sognarsi di trovare un VERO sistema inerziale. Sempre e soltanto qualcosa che si adatti alla situazione che si vuole studiare...
Poi parli di sistemi doppi e/o di sistemi satellitari e ti poni problemi sul baricentro. Questo non l'ho proprio capito. Cosa c'entra con la giostra o con qualcosa in cui l'accelerazione centripeta non deriva dalla gravità? Siamo proprio nel caso della forza gravitazionale, in cui vale la legge di Newton. Se il baricentro si sposta non cambia di certo la forza centripeta... Scusa, ma non riesco a capire il problema...
Subito dopo, infatti, torni sulla giostra e quindi escludi di nuovo la forza gravitazionale come "mandante".
Poi, dopo tanti bellissimi, ma divaganti, paragoni, arrivi su una ruota che esce dal campo gravitazionale terrestre e anche solare o galattico. OK... possiamo dire che nessuna massa esterna influenzi il moto di rotazione. Beh... questo è abbastanza simile al caso della giostra sulla Terra. Una rotazione locale subisce ben poco gli effetti perturbativi di masse enormi, ma distanti. In altre parole, anche se ci fossero, rientrerebbero benissimo in un sistema inerziale, come lo è la Terra rispetto alla giostra.
Adesso arriviamo alla conclusione. Nel sistema inerziale impartisci una rotazione alla ruota, qualsiasi sia il motore che vuoi usare. Parliamo di velocità che è più che sufficiente. Il punto P che sta sul bordo esterno della ruota o quello che sta vicino al mozzo centrale si muovono tutti con la stessa velocità che, OSSERVATA DA UN OSSERVATORE ESTERNO (inerziale), tenderebbe a far muovere questi punti lungo una traiettoria rettilinea e uniforme. Non lo riescono a fare perché i vincoli della struttura li tengono uniti tra loro e anche al mozzo centrale. Cosa vedo dall'esterno? Tanti punti che variano istante per istante la loro velocità e allora posso solo concludere che esiste un'accelerazione centripeta (e quindi anche una forza che l'ha generata). Niente di diverso rispetto alla giostra sulla Terra. Al limite, dovrai dare più gas per riuscire a ottenere una certa velocità... Non esiste nessuna forza centrifuga, perché se tu staccassi il punto P dal resto della ruota lui se ne andrebbe per la tangente con un moto rettilineo uniforme (non subisce più nessuna accelerazione centripeta).
Ben diversa è la situazione spiegata da un punto che è legato alla ruota e che vede le cose dal sistema rotante. Ma tu non parli di questo problema che è, invece, quello fondamentale per il mio articolo. E, non volendo creare confusione attendo di descriverlo nella seconda parte con molta calma e attenzione e semplicità massima.
Non capisco poi cosa significhi :
Un giro ogni due sec attorno a un asse mi deve generare una “finta gravità” rivolta verso l’esterno (che altro non è che forza centrifuga che io vivo come gravità)uguale a quella che misurerei se fossi in orbita attorno a Urano?
No, assolutamente no. La rotazione non genera una finta gravità diretta verso l'esterno. Anzi, non capisco proprio cosa possa essere una forza di gravità diretta verso l'esterno. la ruota che gira crea un vincolo che "piega" la velocità e che quindi manifesta senza ombra di dubbio che esiste una forza centripeta, diretta verso l'interno e che simula quella della gravità. Tutto ciò, sempre e comunque, visto dall'esterno della ruota.
Poi, dopo varie simpatiche amenità, concludi con:
come se la nettezza del tratto grafica di quei tre assi xyz dipendesse dalla presenza di masse adeguatamente prossime che lo legittimino… come se un pochino, la legge quadratica inversa influenzasse anche l’autorevolezza del riferimento…
Le masse esterne non influenzano (come già detto), il moto della ruota e la sua forza centripeta che dipende dal motore che dona una velocità a ogni punto della ruota ma gli impartisce la forza centripeta dato che non li fa scappare per la tangente..
Insomma, non ho capito ancora cosa ti turba e cosa non capisci... scusa, ma sarò un po' "tardo"... ma non ci riesco proprio...
AIUTO!!!!
Attenderò con ansia... grazie per ora a lucianodev per essersi posto il problema di porsi nei miei panni...
 Buona Pasqua a tutti.
Buona Pasqua a tutti. 
In effetti, per sapere se ho iniziato o no (magari lentissimamente per non notare l'accelerazione tangenziale) una rotazione secondo un asse, mi basta constatarne l'effetto, questo lo capisco: se dentro la "ruota" di Von Braun, misuro un'accelerazione verso l'esterno, che dal mio punto di vista assume il pratico ruolo di una gravità artificiale, "vuol dire che sto ruotando", ossia individuo la causa dall'effetto, è l'effetto che mi è indice della mia condizione di corpo che ruota su se stesso. Anche se guardando fuori è tutto nero come la pece (modo casareccio per dire "non ci son masse significative a una distanza decente tale che io possa pensare mi stiano influenzando significativamente sulla mia scala").
Di più. Posso verificare il mio assetto nel Cosmo anche senza avere nemmeno un'oblò o un sensore esterno, se solo prima del lancio accelero un raffinato giroscopio e lo tengo a girare tutto il tempo. Tenderà ad opporsi, con una inerzia proporzionale al suo momento angolare, dipendente dalla velocità di rotazione oltre che dalla massa, ad ogni variazione della direzione del suo asse... un perfetto riferimento inerziale tascabile!
E allora dov'è che mi ingrippo? E' sull'idea che in un certo senso, per valere, è come se... il riferimento inerziale esterno "sapesse" tener conto della distribuzione di tutta la massa dell'Universo... un abisso, per me.
Su, su, aspetto.
caro Valerio,
se tu sei nel sistema rotante, sentirai una forza centrifuga "fittizia" che viene annullata da quella centripeta (i vincoli). Su questo non si scappa e a nulla servono le masse esterne. Tu ti senti fermo, ma per un osservatore esterno non lo sei assolutamente e per lui non esiste alcuna forza centrifuga. Hanno,ovviamente, ragione tutti e due perché il sistema rotante NON E' INERZIALE! Tutto lì... niente di più e niente di meno. Se poi qualcuno ti telefona e ti dice che ruoti puoi anche crederci, ma tu sei comunque fermo nel tuo sistema di riferimento. E non esiste nessuna forza gravitazionale diretta verso l'esterno... E poi parli di accelerazione tangenziale, di cui non c'è assolutamente bisogno in una ruota che gira. Anzi, non esiste proprio nel moto circolare uniforme... tutta l'accelerazione è centripeta e basta. La puoi usare solo per raggiungere una certa velocità che vuoi tu, ossia proprio quella che simula una gravità fittizia (basta uguagliare certe quantità...). va bene, ne parliamo dopo l'uscita del post completo... Buona Pasqua!
Forse è ora di introdurre il concetto di forza o è ancora troppo presto?
@Valerio:
Per sapere se e come stai ruotando basterebbe fare dei segni nelle pareti dell'astronave.
Se fossi in caduta libera galleggeresti nella tua cabina, e con te tutti gli oggetti, privi di peso.
Se l'astronave ruotasse su un asse, verresti spinto verso le pareti esterne, opportunamente contrassegnate.
Per quanto riguarda Von Braun, con tutto il rispetto, mi sembra che la sua ruota sia irrealizzabile... a che velocità dovrebbe ruotare per simulare la gravità esercitata dalla massa della Terra?!?
Inoltre in alcuni punti mi sembra che tu confonda la velocità tangenziale con l'accelerazione tangenziale.
L'accelerazione tangenziale la tiravo in ballo per la fase in cui con non meno di due piccoli propulsori disposti a 180° l'uno dall'altro applicavo una forza propulsiva per far ruotare secondo il suo "mozzo" la ruota di Von Braun.
Questa, peraltro, fu vaticinata da lui per l'estrema facilità con la quale, in una astronave molto grande come quella da lui immaginata (un centinaio di metri di diametro se non di più) con una velocità angolare relativamente piccola si poteva simulare un'accelerazione verso l'esterno (che in realtà, come giustamente rimarcava Enzo, è fittizia trattandosi in realtà della reazione vincolare della struttura verso il centro dell'asse di rotazione, ossia in effetti una forza centripeta) assolutamente accettabile per le esigenze di vita di un astronauta. Diciamo dell'ordine di 5-6 (m/sec)2.
Per avere un'accelerazione apparente verso l'esterno assai grande basta una velocità di rotazione abbastanza bassa: io stesso tanti anni fa potei vivere su me stesso l'esperimento di una gravità artificiale in un cilindro rotante, alle cui pareti mi dovevo appoggiare a braccia semiaperte, e che iniziava a ruotare. Raggiunta una certa velocità, il pavimento su cui inizialmente i miei piedi poggiavano si abbassava di un paio di metri, ma la forza centrifuga era ampiamente sufficiente a generare un attrito fra il mio corpo e le pareti del cilindro, da sovrastare con facilità l'attrazione gravitazionale verso il basso, che peraltro quasi non percepivo più, avendo la sensazione, ovviamente, di essere sdraiato sulla schiena. E' cosa di molti molti anni fa, e ricordo grossomodo che il diametro del cilindro non era forse superiore a 5-7 m, e che girava a - grossomodo - più di 360°/sec e meno di 720°/sec. Ero sottoposto a una accelerazione apparente verso l'esterno se non rammento male superiore al mio peso, anche se non di molto.
Ora, il mio problema di comprensione, sottile e drammatico, non è come si svolga il fenomeno, e che effetti abbia: quelli la mia mente bacata li "vede" bene da quando ero bambino, e su tanti libri era raffigurata la "ruota" di Von Braun. Infatti ho scritto poco sopra più o meno, se nella ruota percepisco - essendo solidale alla sua struttura, ovvio - che "peso" verso l'esterno, e ciò non avviene in una direzione sola precisa (allora l'accelerazione sarebbe lineare = motori accesi) ma in tutte le direzioni a partire da un asse, allora posso dire « rispetto a un sistema inerziale esterno, devo star girando attorno a un asse, che è normale alla direzione in ogni punto della circonferenza della "ruota" verso la quale mi sembra di "pesare" ».
Il mio problema è che non "vedo" con altrettanta ineluttabilità la necessaria costanza del valore della stessa forza apparente, che la fisica mi dice a parità di parametri dover essere lo stesso ovunque, e se non erro ciò si definisce principio di equivalenza. "Ci credo", naturalmente, ma non lo "vedo" con la stessa evidenza, nel caso mi trovi in un punto dell'Universo lontano da qualunque concentrazione di masse. Il che percepisco essere contradditorio, ma è un mio problema.
Bellisimo e molto chiaro, Grazie Enzo per queste chicche... Sono veramente uniche...