Questo è il sesto articolo della serie "Ponti sospesi, catenarie, parabole & co."

Affrontiamo lo scoglio maggiore di questa serie di articoli, ossia determiniamo l'equazione della catenaria, quella "strana" condizione di equilibrio di una catenella sospesa tra due chiodi intorno alla quale Galileo ha disquisito, accorgendosi di non essere in grado di ricavarla e accontentandosi di approssimarla a una parabola.

Prima di iniziare la parte più matematica, cerchiamo di vedere la situazione in modo puramente concettuale. La traiettoria di un proiettile è data dalla somma di due moti: uno rettilineo uniforme e uno diretto verso l'alto con la conseguente ricaduta a causa della gravità. In altra parole, un moto a velocità costante e uno ad accelerazione costante. Moti, comunque, che sono eseguiti su rette tra loro perpendicolari. La parabola non è altro che la combinazione di due moti e risulta abbastanza chiaro che il risultato sarà un'equazione di secondo grado in x, ossia una parabola (l'accelerazione introduce il quadrato e la velocità il termine lineare). Non voglio confondere, ma solo cercare di far notare alcune differenze sostanziali. La catenaria, ossia la forma che assume la nostra catenella sospesa può essere considerato una somma di moti congelati, o -ancora- meglio l'equilibrio, ossia la situazione di stallo, ottenuta applicando tre moti. Uno di questi è sempre dovuto alla gravità, mentre gli altri due sono in qualche modo uno opposto all'altro (ma non esattamente uguali!): una specie di "tira e molla". L'importante è però che la gravità agisce sempre lungo l'asse delle ordinate, mentre le altre due forze NON agiscono lungo l'asse delle ascissa, ma proprio lungo la catenella stessa. Sperare che venga fuori una parabola sarebbe a dir poco troppo pretenzioso. La natura si inventa qualcosa di apparentemente più complesso, ma che, in realtà, a parte la difficoltà di determinarlo per via analitica, segue proprio la via della semplicità naturale.

Scusate questo inizio più filosofico che scientifico, ma  a volte la Natura va interpretata e bisogna fare uno sforzo per cercare di seguire i suoi ragionamenti che per noi e per il nostro linguaggio matematico possono sembrare complicati. Vedremo, alla fine, che per ottenere la curva che a noi sembrerebbe forse la più ovvia (la parabola) basta solo modificare leggermente le caratteristiche della fune, deformando in qualche modo la maggiore generalità e semplicità della catenaria.

Va bene... cominciamo e cerchiamo di andare avanti a piccoli passi, in modo da poter essere seguiti da tutti coloro che hanno una minima conoscenza di derivate e di integrali. I quattro asterischi sono relativi più che altro alla "pazienza" dei lettori...

Appendiamo, allora, in A e B, la nostra catena che raggiunge immediatamente la sua condizione di equilibrio (Fig. 1).  Noteremo tra breve che non è assolutamente necessario che i due chiodi alla quale è appesa siano posti alla stessa altezza.

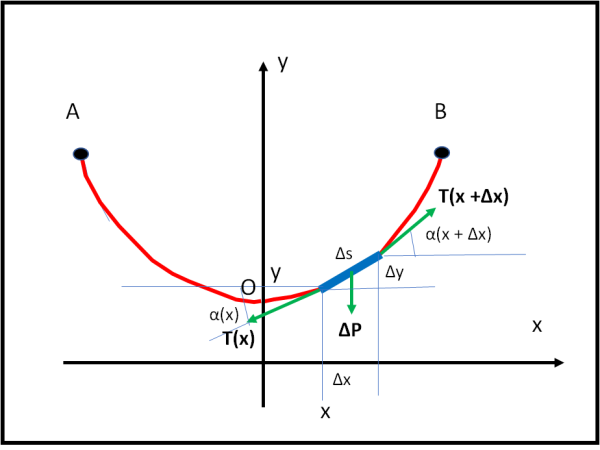
Per prima cosa dobbiamo scegliere degli assi di riferimento e, come quasi sempre, non ci facciamo mancare gli assi cartesiani x e y. Li scegliamo, però, con qualche piccola precauzione. L'asse y deve passare per il punto più basso O della catenella e avere il verso positivo verso l'alto (in tal modo divide anche la catenella in due parti esattamente uguali per simmetria). L'asse x deve essere perpendicolare all'asse y, ma poco importa la sua distanza dal punto O della catenella. La cosa è del tutto ininfluente, dato che l'asse delle x  sarà scelto proprio per avere la sua distanza dal punto O esattamente uguale all'unico parametro  che contraddistingue l'intera curva.

Su un qualsiasi elemento della catenella (di lunghezza Δs) agisce la forza peso ΔP che vogliamo esprimere attraverso la densità del materiale di cui è composta la catenella, immaginata a sezione circolare di area uguale ad A.

ΔP = Δm g                                           (seconda legge della dinamica)

ΔP = ΔV ρ g                                        (la massa è uguale al volume ΔV dell'elemento, moltiplicato per la densità ρ)

ΔP = A ρ g Δs                                     (L'elemento considerato ha forma cilindrica di area A e di altezza Δs)

N.B.: Questo è il punto veramente fondamentale che discosta la nostra curva dalla parabola. In questo caso manteniamo ρ costante, ossia costante la forza peso per ogni elemento Δs della catenella. Se la forza peso variasse uniformemente la curva si "complicherebbe" diventando una semplice parabola.

Sull'elemento che subisce il peso ΔP agiscono altre due forze date dalla tensione del resto della catenella. Un diretta verso il basso e a sinistra T(x)(di segno negativo) e una diretta verso l'alto e a destra di segno positivo T(x + Δx).

L'equilibrio sull'elemento di lunghezza Δs si ha quando le tre forze, con il loro segno, si annullano. Scriviamo questa condizione per le due coordinate lungo x e lungo y:

- T(x) cos α(x) + T(x + Δx) cos α(x + Δx)  = 0

- T(x) sen α(x) + T(x + Δx) sen α(x + Δx)  - ΔP = 0

divido la prima per  Δx (≠ 0) e ottengo un bel rapporto incrementale della funzione T(x) cos α(x)

(T(x + Δx) cos α(x + Δx)  - T(x) cos α(x))/Δx= 0

rendendo  Δx sempre più piccolo il primo membro diventa la differenza sempre più piccola di T(x) cos α(x) rispetto a dx, ossia la sua derivata rispetto a x

d(T(x) cos α(x))/dx = 0

ossia

T(x) cos α(x) = T₀ = costante                       .... (1)

Differenziando anche la seconda equazione, possiamo scrivere:

d (T(x) sen α(x)) = dP                                              .... (2)

Ma dalla (1) sappiamo che

T(x) = T₀/ cos α(x)

Sostituendo nella (2), otteniamo

T₀ d(tan(x)) = dP

Sappiamo però anche che

tan(x) = dy/dx = y'                                    (usiamo il simbolo y' per la derivata di y rispetto a x per comodità di scrittura)

Per cui si ha:

T₀ d(y') = dP

T₀ d(y') = A ρ g ds                              .... (3)

Tuttavia, possiamo ancora esprimere ds in funzione di dx e dy. Basta applicare Pitagora...

ds = √( dx² + dy²)

Ma sappiamo che dy = y' dx e possiamo sostituirlo

ds = √( dx² + y'² dx²) = dx√(1 + y'²)

Sostituendo nella (3)

T₀ d(y') = A ρ g dx√(1 + y'²)

T₀ d(y')/dx = A ρ g √(1 + y'²)

T₀ y'' = A ρ g √(1 + y'²)                    .... (4)

che equivale a (usando la terminologia usata nelle equazioni differenziali)

T₀ d²y/dx²= A ρ g √(1 + (dy/dx)²)

Bene, siamo arrivati al punto chiave della trattazione. Dobbiamo risolvere un'equazione differenziale non certo banale come quelle trattate QUI.

E' ora di fare il primo trucchetto...

Perché portarci dietro la y' che compare sia a sinistra che a destra? Cominciamo a chiamarla in altro modo e a tempo debito le ridaremo la sua vera identità. E' o non è anch'essa una funzione di x? Sì! e, allora, chiamiamola z(x). La (4) diventa:

T₀ z' = A ρ g √(1 + z²) 

Scriviamola nel modo che meglio conosciamo e separiamo le variabili...

T₀ dz/dx = A ρ g √(1 + z²)

dz/√(1 + z²)   =  dx

Non ci resta che integrare entrambi i membri

∫(1/√(1 + z²)) dz = (A ρ g/T₀)∫dx = (A ρ g/T₀) x + c

Eh sì... dobbiamo ancora risolvere l'integrale del primo membro e qui bisogna proprio usare la furbizia e l'esperienza. In pratica, bisogna trovare una funzione la cui derivata prima sia proprio 1/√(1 + z²).

Un calcolo non banale

La parte che segue può anche essere saltata, ma è, comunque, un bel banco di prova sia per ricordarsi le derivate non banalissime, sia per vedere quanto più difficile e fantasiosa sia l'operazione inversa.

Eseguiamo un doppio percorso, in modo che possa essere seguito anche solo nella sua prima parte:

Calcoliamo una derivata.

Prendiamo questa bella funzione:

t = ln(z + 1/√(1 + z²))

e facciamone la derivata

Essa è chiaramente una funzione composta , per cui dovremo anche moltiplicare  per la derivata dell'argomento

t' = (1 /(z+ √(1 + z²))) d((z + √(1 + z²))/dz

t' = (1 /(z + √(1 + z²))) d((1 + z²)^1/2 + z)/dz =

(1 + z²)^1/2 è anch'essa una funzione composta per cui dobbiamo ricordarci di moltiplicare anche per la derivata di (1 + z²)

t' = (1 /(z + √(1 + z²))) ((1/2)(1 + z²)^{(1/2) - 1} )d(1 + z²)/dz ) + dz/dz)

t' = (1 /(z + √(1 + z²))) ((1/2)(1 + z²)^-1/2 )d(1 + z²)/dz ) + 1)

dobbiamo ancora eseguire una derivata (facile questa volta)

t' = (1 /(z + √(1 + z²))) ((1/2)(1 + z²)^-1/2  (0 + 2z) + 1)

t' = (1 /(z + √(1 + z²))) ((((1/2)/√(1 + z²)) 2z) + 1) 

t' =(1 /(z+ √(1 + z²))) ((1 /√(1 + z²)) z) + 1) =

t' = (1/(z + √(1 + z²))) (z /√(1 + z²))+ 1) =

ponendo √(1 + x²) come comune denominatore della seconda parte

t' = 1 /(z + √(1 + z²))(z + √(1 + z²)) /√(1 + z²)

t' = 1/√(1 + x²)

Guarda caso la nostra derivata è proprio la funzione di cui dobbiamo fare l'integrale. Ne segue che la funzione di partenza è proprio il risultato dell'integrale!

Sì, sì, tutto bene... un bell'esercizio di attenzione e pazienza... ma, per quale motivo dovevamo scegliere proprio quella funzione apparentemente così diversa?

Calcoliamo un integrale con i "fiocchi"

La vera cosa da fare è cercare di immaginarsi un pochino come potrebbero andare l faccenda e poi maneggiare un po' sull'integrale per farlo diventare "fattibile" e decisamente più semplice. In tutto ciò ci vuole non solo esperienza e pazienza, ma anche un guizzo di fantasia... Il punto chiave è comunque quello di cominciare a pensare ai logaritmi quando si ha a che fare con una funzione che ha un'espressione al denominatore (la derivata del logaritmo di z è uguale a 1/z).

Prendiamo allora il nostro integrale e mettiamolo sotto torchio

∫(1/√(1 + z²)) dz 

Cominciamo col porre 

u = z + √(1 + z²)                             .... (5)                    (dove u è un parametro ausiliario)

√(1 + z²) = u – z

√(1 + z²)² = (u – z)²

1 + z² = u² – 2uz + z²                  

1 = u² – 2uz

2uz = u² – 1

z = (u² – 1)/(2u)                      .... (6)

Abbiamo espresso z in funzione della sola u e possiamo derivare rispetto a u

dz/du = (2u(2u) - (u² -1)2)/(4u²)

dz/du = ((4u² – 2(u² – 1))/(4u²)

dz/du = (2u² + 2)/(4u²)

dz/dt= 2(u² + 1)/(4u²) 

dz/dt = (u² + 1)/(2u²)

Possiamo esprimere dz in termini di u e du

dz = ((u² + 1)/(2u²)) du

Torniamo al nostro integrale iniziale

∫(1/√(1 + z²)) dz 

e inseriamo al posto di z il suo valore come funzione di u, ricordando che quadrando la (6) si ha:

z² = (u² -1)²/(4u²)

∫(1/√( 1 + (u² – 1)²/(4u²)) ((u² + 1)/2u²) du =

= ∫( 1/√( u⁴ – 2u² + 1 + 4u²)/(2u))((u² + 1)/2u²) du =

= ∫(2u/√(u⁴ + 2u² + 1)) ((u² + 1)/(2u²)) du =

= ∫(1/√(u² + 1)²) ((u² + 1)/u) du =

= ∫(1/(u² + 1) ) ((u² + 1)/u) dU =

= ∫(1/u) du =

= ln u + C =

ma, ricordando la (5) si ha infine:

∫(1/√(1 + z²)) dz = ln (z+ √(1 + z²)) + C

C.V.D.... ma che fatica!

Ho volontariamente eseguito tutti i passaggi, anche i più semplici, proprio per permettere a chiunque di risolvere questo integrale non certo facile. L'idea originaria della sostituzione è la parte fondamentale, ma accettandola con fiducia non ce ne siamo pentiti.  Ritorniamo alla nostra catenaria...

Risolto l'integrale, possiamo scrivere:

∫(1/√(1 + z²)) dz =  (A ρ g/T₀) x + c

ln (z + √(1 + z²) = (A ρ g/T₀) x + C1                         (C1 tiene conto anche dell'ultima integrazione)

Chiamiamo

A ρ g/T₀ = 1/a

Pensiamo un attimo alla costante d'integrazione...

La tangente alla catenaria nel suo punto più basso deve essere uguale a zero. Ossia:

y'(x = 0) = 0

e quindi anche

z(x = 0) = 0

Questa condizione ci permette di determinare C1, inserendo x = 0 (e quindi z = 0) nell'equazione risolvente

ln (z + √(1 + z²) = (A ρ g/T₀) x + C1

ln( 0 + 1) = 1/a · 0 + C1

ln (1) = C1

C1 = 0

Per cui abbiamo l'equazione che segue:

ln (z + √(1 + z²) = (A ρ g/T₀) x =  x/a

Non ci resta che eliminare il logaritmo utilizzando il solito numero e:

e ^{ln (z + √(1 + z · z)} = e^x/a

z + √(1 + z²) = e^x/a                    .... (7)

Molto bene... adesso possiamo divertirci un po' con passaggi poco più che elementari.

Moltiplichiamo entrambi i membri per  z - √(1 + z²), ricordando il solito prodotto notevole (a + b)(a - b) = a² - b²

(z - √(1+ z²))(z + √(1+ z²)) = (z - √(1+ z²)) e^x/a

z² - (1+ z²) = (z - √(1+ z²)) e^x/a

-1 = (z - √(1+ z²)) e^x/a

ricordando che 1/e^x/a = e^-x/a

- e^-x/a = z - √(1+ z²)                     .... (8)

Sommando la (7) e la (8) abbiamo:

z + √(1 + z²) + z - √(1+ z²)  = e ^x/a - e ^-x/a

2z = e ^x/a - e ^-x/a

z = (e ^x/a - e ^-x/a)/2

Finalmente qualcosa che abbiamo imparato a conoscere molto bene: il seno iperbolico!

z = senh(x/a)

Ma, non dimentichiamoci chi è veramente z. Ormai ha svolto il suo prezioso compito e possiamo tornare a scrivere:

y' = z e quindi

y' = senh(x/a)                                 .... (9)

Dobbiamo integrare ancora una volta, ma questa è un'operazione banale ricordando (QUI) che la derivata del cosh(x) è proprio il senh (x).

y =∫senh(x/a) dx

Scriviamo la (9) moltiplicando e dividendo per a il secondo membro

y = a∫(1/a )senh(x/a) dx

All'interno dell'integrale abbiamo proprio la derivata di cosh(x/a) ed è per questo che ci siamo "creati" 1/a che è la derivata dell'argomento (x/a)

Ne segue che l'integrale della (9) è proprio la funzione che cercavamo fin dall'inizio

y = a cosh(x/a) + c

Basta scegliere c in modo che la catenaria abbia la y del suo punto più basso uguale ad a. Il che vuol dire c = 0 dato che per x = 0, y = a.

In conclusione:

y = a cosh(x/a)

Questa curva dipende in pratica solo e soltanto dal parametro a. Se tale parametro non fosse costante la faccenda cambierebbe in modo relativamente più semplice. Facendo i conti se  la densità variasse linearmente con la distanza dal punto più basso della curva, in senso orizzontale, avremmo che l'integrale del prodotto tra a e x non varrebbe solo ax, ma spunterebbe fuori una x² e la nuova curva sarebbe proprio una parabola!

Si otterrebbe, in pratica, una curva del tipo:

y = x²/2a + a

La Fig.2 illustra la differenza tra parabola e catenaria.

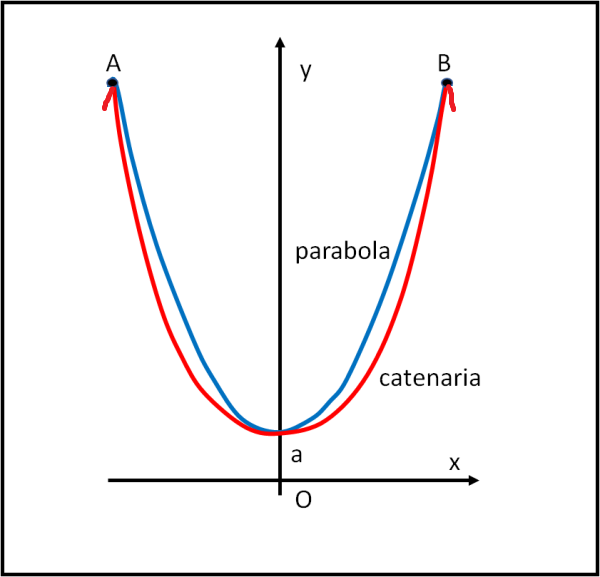
In fondo Galileo aveva ragione : per angoli non superiori a 45° le due curve si sovrappongono quasi perfettamente, Anzi senza il quasi per la tecnologia di quei tempi. 

Notare che la catenaria è più "piatta" della parabola. Questo è dovuto alla loro distribuzione di peso. Il ponte sospeso ha lo stesso peso per ogni elemento orizzontale, mentre la catenaria no. Vi è un peso relativamente maggiore lontano dal punto centrale, dove la curva è più ripida. Perciò c'è più catenaria in ciascun intervallo rettilineo unitario. Questo fatto rende più leggera la catenaria lontano dal centro, dato che le viene imposto un peso sempre uguale per lunghezze crescenti della catenaria.

P.S.: sembrerebbe impossibile che una curva in cui sia costante la densità diventi più faticosa a determinarsi di quella che ha invece una densità variabile (la parabola di vertice in V(0.a) si troverebbe velocemente). Cerchiamo di rispondere in modo fisico e non puramente geometrico o analitico. Nella catenaria gli unici "moti" (fatemeli chiamare così), sono quello verticale e quello lungo la catenella. Questo sulla catenella si riversa sia su x che su y e rende l'equazione del "moto" più complicata. Quando invece lavoriamo con una x che comanda la densità della catenella, variando in modo rettilineo uniforme l'ungo la "strada", ci riconduciamo proprio al caso della traiettoria parabolica: un moto orizzontale rettilineo uniforme e uno verticale legato al peso. La curva, in qualche modo, si semplifica e coincide con la parabola.