Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure

Premessa.

Se vogliamo addentrarci correttamente alla comprensione delle varietà Riemmane, abbiamo bisogno di qualche concetto riguardante argomenti di matematica avanzata,  che di solito di studiano nei primi due anni di università . Chiaramente non è nei nostri scopi né nelle nostre possibilità approfondire tali argomenti. Provo perciò a presentarli in modo pratico-intuitivo,  sfruttando anche il lavoro fatto da Vincenzo e  da Fabrizio. Parleremo di matrici e del loro prodotto, di derivate parziali e equazioni parametriche, nonché di prodotti scalari. Spero che questo sia sufficiente per comprendere uno dei concetti più belli e potenti della matematica che è alla base delle teorie relativistiche e della cosmologia: le varietà Riemmane.

visto il percorso fatto --> varietà topologiche-->varietà differenziabili ci sarà facile  darne  (almeno)la definizione formale:

Una varietà Riemmana è una varietà differenziabile dotata di metrica. Già, ma cos'è una metrica? Lo abbiamo visto in modo molto generale qui, dove ci si riferiva ad un insieme qualsiasi.. ma qui la struttura a disposizione (varietà differenziabili) è molto più ricca, e possiamo parlare di coordinate. Infatti, dove abbiamo a che fare con delle coordinate possiamo definire una distanza partendo da un prodotto scalare (funzione che a due vettori associa uno scalare).

La  definizione di distanza.

Ricordiamo un attimo la definizione di distanza ovvero le proprietà a cui deve  soddisfare d:X x X--->R in un insieme X qualsiasi:

1)d(x,y)

2) d(x,y)=0 se (e soltanto se) x=y

3) d(x,y)=d(y,x) simmetria

4) d(x, y) + d(y, z) ≥ d(x, z) che continuiamo a chiamare diseguaglianza triangolare.

C'è un modo di operare per definire la distanza quando si ha a che fare con spazi con coordinate, (ovvero spazi in cui sia definibile una base ), ed è quella di definire un prodotto , detto scalare, di cui abbiamo tutti sicuramente sentito parlare, e di cui si è parlato più volte in questo sito, però in modo un po' diverso. Ma cominciamo dall'inizio.

Intermezzo: la base di uno spazio vettoriale

Dobbiamo per un attimo abbandonare i concetti generali di varietà per metterci a lavorare in  (per adesso in ).  è uno spazio di vettori; ogni punto P di  (o , più in generale, di ) individua un vettore che parte dall'origine O e la cui punta corrisponde al punto P .

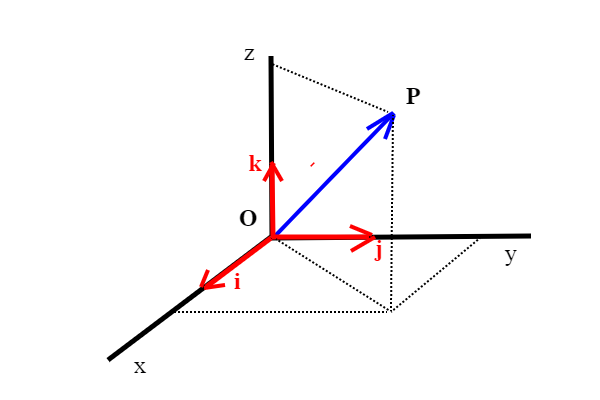
Definiamo in due parole cos'è una base in uno spazio di vettori; sappiamo che , ad esempio in un piano, possiamo scomporre un vettore in due vettori usando la regola del parallelogramma, quindi lungo due direzioni fissate. Chiaramente potremmo farlo anche con tre vettori, scomponendo uno dei due in altri due vettori. Ma noi siamo interessati al numero minimo di  direzioni sufficienti a scomporre tale vettore. Si parla anche di dimensione dello spazio in questione. Nel caso del piano la dimensione è due, nel caso dello spazio euclideo la dimensione è tre. Detto in modo più formale, dato uno spazio di vettori (che possiamo ben immaginare cosa sia) chiamiamo base un insieme di vettori ciascuno dei quali sia non nullo, e che generi tramite combinazioni dette "lineari"*, tutti i  vettori di tale spazio. Per esprimere un vettore tramite una base nel piano, abbiamo bisogno di due direzioni e di due numeri, detti coordinate.Per esprimere un vettore tramite una base nello spazio, abbiamo bisogno di tre direzioni e di tre numeri, detti coordinate.  i,j,k  nella figura è una base dello spazio tridimensionale;

*(esempio di combinazione lineare; dati i vettori  a,b,c e gli scalari x,y,z una  combinazione lineare dei tre vettori è il vettore d= xa + yb +zc)

Calcolare il prodotto scalare usando le coordinate di un vettore.

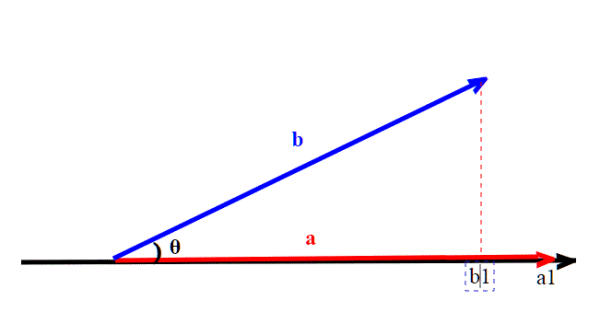
La definizione più nota   di prodotto scalare è la seguente; se indichiamo con |a|, |b| i moduli dei vettori di cui fare il prodotto, e  l'angolo fra di essi, sappiamo che il prodotto scalare (, è dato da :

. Considerato il fatto che ci troviamo in un piano, e avendo a disposizione le coordinate , (assumendo come asse delle x  quello contenente il vettore a) possiamo semplicemente scrivere :

.

Infatti b1 rappresenta proprio la proiezione di b su a, nonché la coordinata rispetto all'asse x. Ma estendiamo questo discorso alle altre dimensioni:

Per il generico spazio di dimensione n si Ha:

o scritto in modo più compatto, usando il simbolo di sommatoria:

quindi, per n=2 :

per n=3

Notiamo che  il prodotto scalare è simmetrico ()  .

Ma perchè è così importante il prodotto scalare?  Esso ci permette  di definire delle proprietà geometriche importanti, quali la distanza o l'angolo fra due vettori. Vediamo come definire la distanza: introduciamo prima la norma di un vettore (che altro non è che la lunghezza del vettore),in tal modo:

; il radicando è infatti sempre positivo, essendo , ovvero una somma di quadrati.

Per definire poi la distanza fra due punti, prendiamo il vettore(differenza) che li unisce; per trovare la distanza fra i punti individuati dalle punte delle freccie dei vettori a,b, prendiamo la norma della differenza fra i due vettori:

è possibile verificare che la distanza così definita soddisfa le proprietà 1) 2) 3) 4) scritte sopra.

Mettiamoci ora in , e vediamo che  ogni vettore è rappresentabile tramite i vettori ortogonali i,j opportunamente combinati linearmente:

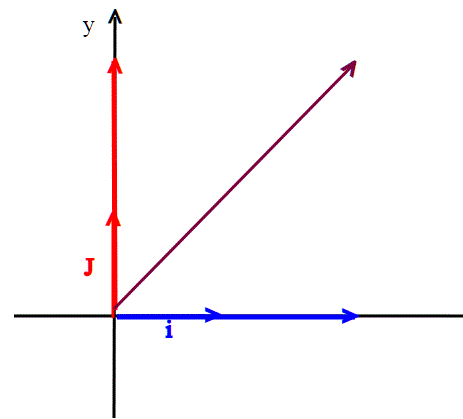
se identifichiamo ogni vettore con una coppia di numeri reali, coordinate delle punte dei vettori, il prodotto scalare risultauna applicazione:

;

ora, se il prodotto scalare è dato dalla formula sopra (per n=2)   ci proponiamo di trovare una matrice, con determinate proprietà, che assumerà una grande importanza nel seguito del discorso. Essa ci permetterà di scrivere in modo compatto le operazioni di questo tipo sui vettori. Se ricordate o qualcuno vi ha mai spiegato quali operazioni si possono fare con una matrice, allora sapete cos'è il prodotto righe per  colonne. Se non lo sapete, allora potete immaginarlo dalla definizione.

Vogliamo trovare una matrice M,  per esprimere il prodotto scalare in forma , per l'appunto , matriciale. Siano a,b due vettori. Possiamo scriverli sia come riga che come colonna.Indichiamo  con  il vettore riga,

il vettore colonna . Il prodotto scalare vogliamo sia espresso da:

dove M è la nostra matrice incognita.

Eseguiamo tale prodotto (righe per colonne):

affinché il termine di destra sia uguale al nostro prodotto scalare,, è sufficiente che sia:

che riscriviamo in forma matriciale:

questa è la matrice del prodotto scalare canonico usuale in . Analogamente, in  abbiamo:

Ricordando ciò che abbiamo visto sopra riguardo alla distanza , possiamo concludere che tale distanza è individuata da una matrice M, detta anche tensore metrico. E qui volevamo arrivare; visto così il termine tensore non sembra che spaventi più di tanto. Ma se ne fa un grande uso nella fisica teorica.

L'equazione di una curva e il vettore velocità

Un altro concetto importante che ci servirà nella prossima puntata è il concetto di equazione di una curva nel piano e nello spazio.

Tutti abbiamo in mente cosa sia una curva nel piano cartesiano. Di solito, però, si è soliti dare  le curve per equazione, come ad esempio l'equazione della circonferenza, ovvero le coppie (x,y) di punti del piano che soddisfano per esempio l'equazione:

altra cosa è dare una curva per parametri. In genere, per una curva piana, si dà una applicazione  e si specifica la corrispondenza fra un parametro (di solito indicato con t) e un punto del piano, cioè 

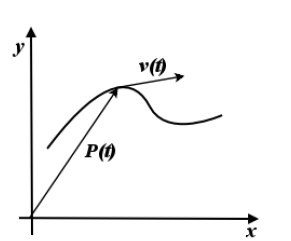
Questo tipo di equazioni ha senz'altro origine da problemi riguardante il moto di un punto; se consideriamo ad esempio un moto parabolico, x,y sono le due coordinate lunghezza e altezza, mentre t è il tempo:

 1)

risulta quindi naturale definire il vettore velocità, v, derivando le due componenti  rispetto al parametro t:

oppure,con una notazione un p0' più vettoriale:

2)

risulta allora evidente l'analogia con la velocità del moto in 1); essa è rappresentata proprio dalle formule appena viste:

Se invece di una curva nel piano, vogliamo considerare una curva nello spazio, poco cambia; basta aggiungere una coordinata alle equazioni parametriche:

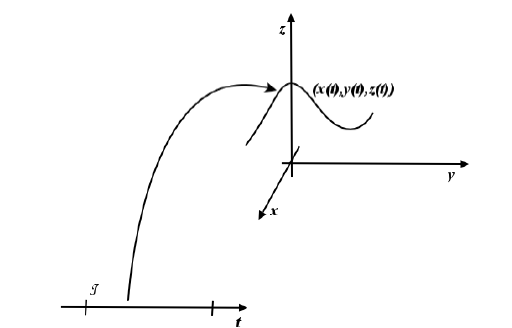
avremo allora, per le equazioni parametriche:

e per la velocità:

Ci fermiamo qui. Nella prossima puntata, tratteremo questi concetti per definire le varietà Riemmane.

Gli altri articoli di questa serie:

0) Un progetto ambizioso

1. LE OMOTOPIE E LA SEMPLICE CONNESSIONE
2. L'ENUNCIATO DELLA CONGETTURA.
3. Le TRI-Varietà topologiche
4. Le varietà differenziabili