Matematizziamo il nastro di Möbius ,parte 1° : Gli Spazi metrici
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Recentemente abbiamo visto degli interessanti articoli (potete trovarli entrambi qui) su quella che si definisce "sartoria topologica" . Questo è il primo di una serie di articoli che ci porterà a capire come è possibile generare matematicamente figure geomatriche tipo il nastro di Moebius senza usare carta e colla.. il percorso non sarà immediato ma nemmeno troppo complesso.
Chi ha nel suo patrimonio culturale personale una conoscenza base degli insiemi e delle relazioni potrà seguire agevolmente senza alcun altro prerequisito. In ogni caso potete trovare in questi link tutto il necessario per proseguire:
insiemi, corrispondenze e funzioni, relazioni di equivalenza.
La trattazione sarà molto intuitiva, anche se le dimostrazioni saranno complete, i disegni dovrebbero aiutare molto per la comprensione.
La topologia in due parole.
Si tratta di un tipo di geometria generalizzata. Si interessa comunque ,per esempio, di sfere e cubi , ma in essa vengono considerati "oggetti uguali". Infatti possiamo prendere uno di essi e trasformalo nell'altro stirandolo o schiacciandolo senza però lacerarlo.
In Topologia è lecita ogni trasformazione continua. Dove per "continua" si intende che punti "vicini" prima della trasformazione, restano tali anche dopo.
Non sottovalutate la topologia che sembra solamente il frutto di menti sofisticate: L'incidenza della Topologia nella scienza moderna è impressionante: la Fisica, a tutti i livelli, dalla Teoria delle Particelle Elementari alla Cosmologia e alla Reletività, ne fa un uso .
Il punto chiave della topologia è la parola omeomorfismo,che è la trasformazione continua a cui accennavamo (dal greco homoios = simile e morphe = forma).
Un’espressione del linguaggio corrente che si avvicina al concetto di omeomorfismo è quella di “A è a forma di B”. Ad esempio l’espressione “il salvagente è a forma di ciambella”, nel linguaggio del topologo è
tradotto “il salvagente e la ciambella sono omeomorfe”. In realtà però sono tra loro omeomorfe anche figure che
non si assomigliano poi così tanto, ad esempio una tazza con il manico e una ciambella sono tra loro omeomorfe.

Per poter parlare di omeomorfismo dobbiamo prima parlare di continuità, ma per definire cosa intendiamo per continuità avendo a che fare con degli insiemi qualsiasi, dobbiamo fornire questi insiemi di un qualcosa in più che è appunto la Topologia dell 'insieme. Se prendiamo un insieme qualsiasi e lo forniamo di una topologia lo facciamo diventare uno spazio Topologico.


Un cerchio e un "otto" non sono invece figure omeomorfe: partendo dall'otto non è possibile realizzare un cerchio senza strappare il punto P che è in comune alle quattro linee.
Una definizione di spazio topologico?
Quando si legge la definizione assiomatica di spazio topologico si può restare immediatamente interdetti. Nella maggior parte dei casi, senza alcun preambolo, si butta là una definizione assiomatica tipo questa:
Una struttura topologica, o topologia su X è una famiglia t di sottoinsiemi di X tale che valgano le seguenti proprietà:
- l’insieme vuoto e X appartengono a t;
- l’unione di una qualunque famiglia di elementi di t appartiene ancora a t;
- l’intersezione di un numero finito di elementi di t appartiene ancora a t.
Gli elementi di t sono aperti della topologia t....
Chiaramente il neofita può restare completamente stupito da queste due definizioni, che sembrano uscire dal nulla. Scopo di questo articolo sarà proprio fare vedere come lo spazio topologico sia una generalizzazione di spazi che già conosciamo. In particolare introdurremo per primi gli spazi metrici. Tralasciamo quindi questa definizione che riprenderemo più avanti. Partiremo dallo spazio Euclideo che tutti conosciamo per arrivare agli spazi metrici e poi alla topologia. In questo modo le definizioni dovrebbero essere più chiare.
Lo spazio Euclideo: il più semplice spazio metrico.
Vediamo sotto un altro punto di vista lo spazio Euclideo che tutti conosciamo; tale spazio può avere diverse dimensioni:
- La retta di dimensione 1
- Il piano , di dimensione 2
- Lo spazio tridimensionale, di dimensione tre.
Sappiamo che i punti di questi spazi sono in corrispondenza biunivoca naturale con ,
,
qualora si fissi una origine e un sistema di coordinate, che ad ogni punto faccia corrispondere le sue coordinate.
In tutti e tre i casi abbiamo una nozione naturale di distanza fra due punti.
Per comodità mettiamoci nel piano. Per trovare la distanza fra due punti dobbiamo semplicemente applicare il teorema di Pitagora:

La distanza P1P2 si ottiene applicando il teorema di Pitagora al triangolo P1CP2: sappiamo che :
1)osserviamo che la distanza è un numero >=0;
2) che è nulla solo nel caso che i punti coincidano;
3)ovviamente P1P2=P2P1 (simmetria)
se prendiamo inoltre tre punti nel piano :
 sappiamo dalla geometria Euclidea, che:
sappiamo dalla geometria Euclidea, che:
4) AB<AC+CB (in un triangolo un lato è sempre minore della somma degli altri due. Questo fatto è noto come diseguaglianza triangolare. Analiticamente, questo si traduce in:
Con questa definizione di distanza, che è quella naturale, lo spazio euclideo diviene uno spazio metrico.
Ma ai matematici piacciono le generalizzazioni:
prendiamo un insieme qualsiasi, X , dove sia definita una applicazione: d: X x X--->R che soddisfi alla 4 proprietà illustrate nell'esempio sopra:
1)d(x,y)
2) d(x,y)=0 se (e soltanto se) x=y
3) d(x,y)=d(y,x) simmetria
4) d(x, y) + d(y, z) ≥ d(x, z) che continuiamo a chiamare diseguaglianza triangolare.
L'insieme X, munito della applicazione d(x,y) diventa uno SPAZIO METRICO.
Come ripeto stiamo generalizzando ; X può essere un insieme qualsiasi. Vediamo un esempio.
Su un insieme qualsiasi X possiamo definire la distanza detta discreta definita da:
d(x, y) =1 se
d(x, y)=0 se x = y.
E' una distanza?
- d(x,y)
(o è 1 o è 0)
- d(x,y)=0 solo se x=y per definzione
- d(x,y)=d(y,x) (la definizione non dipende dall'ordine)
- d(x, y) + d(y, z) ≥ d(x, z); chiaramente i tre punti sono distinti, per cui 1+1>1
Un tale spazio (X, d) `e chiamato spazio metrico discreto.
Un altro esempio addirittura con le funzioni! Sia X l'insieme delle funzioni continue f : [0, 1] → R
definiamo d(f,g)=. Anche questa è una distanza;qualcuno vuole provare a dimostrarlo?
Adesso che abbiamo visto che gli spazi metrici sono oggetti totalmente generali, vogliamo definire in essi un concetto che molti di voi già conoscono dallo studio di funzioni reali di variabile reale, ma in altro modo totalmente generico. Per far ciò abbiamo prima bisogno di un tipo di insieme fondamentale:
Definizione di Bolla in uno spazio metrico.
Sia X no spazio metrico dotato di una certa distanza d; prendiamo un punto x di X, chiamiamo bolla di raggio r, dove r è un certo numero reale maggiore di zero, e centro x, l'insieme : {
tali che
}
Esempi:
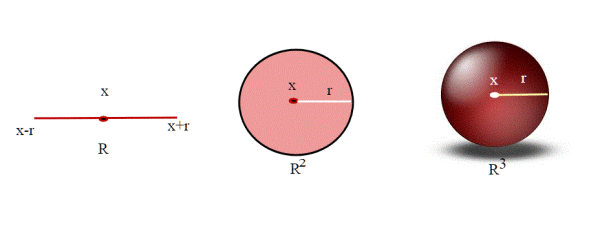
1) In R, con la distanza usuale (|x-y|) la bolla di raggio r e centro x è l’intervallo (x − r, x + r).
2) In , con la metrica euclidea, le bolle di centro x sono dischi centrati in x.
3) In le bolle sono delle sfere piene.
Faccio una parentesi; di recente abbiamo pubblicato un quiz, che potete trovare QUI, in cui abbiamo parlato di distanze un po' particolari, e della forma delle loro bolle.
Continuità
Grazie alla definizione di bolla possiamo dare un'altra definizione, quella di continuità.
Diremo che una funzione fra due spazi metrici f: X-->Y è continua in un punto p, se comunque prendiamo una Bolla di raggio ε e centro f(p) in Y , troviamo una bolla di raggio σ e centro p in X, tale che la sua immagine sia contenuta nella bolla scelta in Y:

detto in termini più formali:
Sia f:X-->Y una funzione fra spazi metrici; diremo che f è continua in se per ogni
>0 esiste un σ>0 tale che
. Diremo poi semplicemente che f:X-->Y è una funzione continua se è continua in ogni punto p di X.
Insiemi aperti
Un altra definizione che ci servirà è che è molto importante, è quella di insieme aperto.
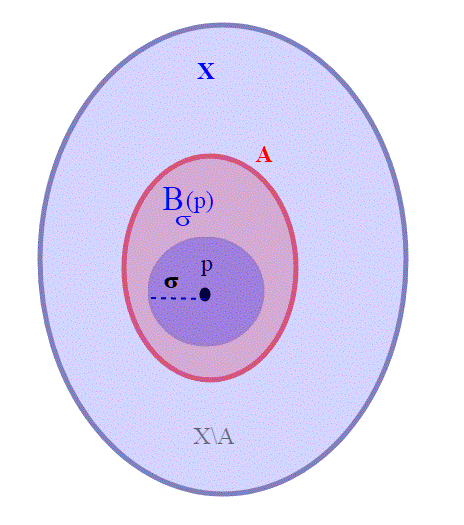
Dato un insieme X con la sua metrica d, definiamo un sottoinsieme
aperto, se comunque scegliamo un punto p appartenente ad A,
, esiste una bolla con centro in p contenuta in A, ovvero più formalmente, esiste un
>0 tale che:
.
A cosa ci fa pensare questa definizione? Al fatto che in tale tipo di insieme ci si può avvicinare quanto si vuole al suo bordo, trovando sempre "infiniti" punti accanto ad esso.
Dopodichè si sfrutta questa definizione per darne un altra:
Un sottoinsieme C di X si dice chiuso se il suo complementare (X\C) è aperto.
In R con la distanza data dal valore assoluto della differenza fra le ascisse di due punti, gli intervalli (a, b) sono aperti mentre quelli di tipo [a, b] non sono aperti (infatti ogni bolla di centro b esce fuori dall’ intervallo [a, b] e quindi non vi può essere contenuta). Gli intervalli di tipo [a, b) oppure (a, b] non sono ne aperti ne chiusi.
Le bolle, in uno spazio metrico, sono sempre aperte.
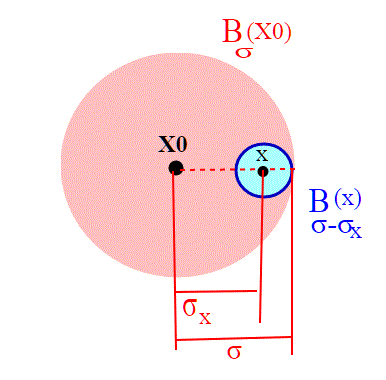
Infatti se ,
,
. E' evidente dal disegno.
Prendiamo adesso uno spazio metrico X con la sua distanza d. Consideriamo gli insiemi aperti di X. allora:
(insieme vuoto) e X sono aperti
non ha punti,quindi è aperto; prendiamo un qualsiasi punto x di X; qualsiasi bolla con centro in X è per forza contenuta in X , basta vedere la definizione di bolla;
{
tali che
}
2 se A1 e A2 sono aperti anche A1 U A2 è un insieme aperto; in generale se al variare dell'indice i sono aperti , anche
è un insieme aperto
(supponiamo infatti che un punto ; allora , per qualche i,
; esiste allora una bolla
, ma tale bolla allora è contenuta anche nell'unione
3 Se A1, A2 sono aperti, anche l'intersezione è un insieme aperto
( se un punto p appartiene all'intersezione , allora appartiene sia ad A1 che A2; ma A1 e A2 sopo aperti,

esistono allora due bolle centrate in p, che stanno rispettivamente dentro A1 e dentro A2; sono concentriche, quindi la loro intersezione che è sempre una bolla (quella più piccola) starà dentro l'intersezione .
L'aver introdotto gli insiemi aperti, ci permette di cambiare la definizione di funzione continua,in questo modo;
Una funzione f: X-->Y fra due spazi metrici è continua se e solo se per ogni aperto A di Y, è un aperto di X.
Supponiamo per prima cosa che f sia continua con la definizione usuale . Sia un aperto. Dato un
, sia
(ricordiamo che dato un insieme A nel codominio, l'insieme è l'insieme degli
tali che la loro immagine f(x) vada a finire dentro A)
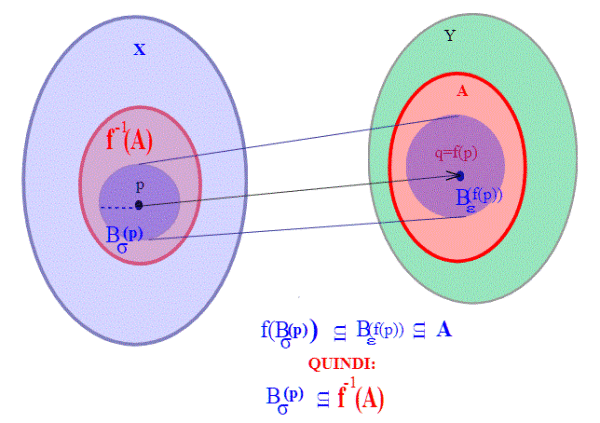
Dobbiamo dimostrare che è aperto, ovvero che esiste una bolla di centro p tutta contenuta in
.
Per ipotesi A è aperto, quindi esiste una bolla di centro f(p) contenuta in A: ; essendo f continua, esiste un altra bolla di centro in p tale che
, ovvero abbiamo trovato una bolla
,quindi
è aperto .
(se l'immagine di un insieme C , f(C) è contenuta in A, allora l'insieme è contenuto in )
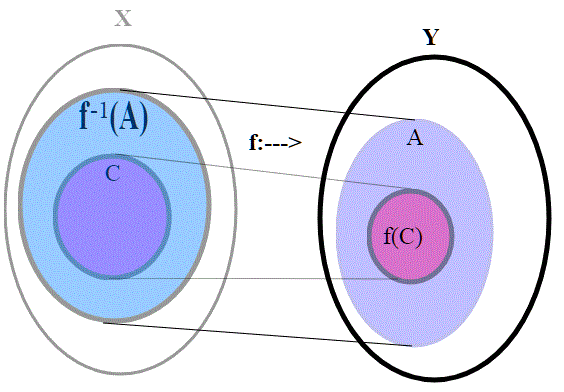
dobbiamo adesso dimostrare l'altra implicazione; supponiamo che per ogni aperto A in Y, sia aperto. Dobbiamo dimostrare che f è continua.

prendiamo ora un e un
>0; la bolla
è un insieme aperto. Quindi per ipotesi
è un insieme aperto e contiene p. Sappiamo allora che esiste una bolla (e un
) con centro in p contenuta in
, ovvero
che implica
.Ma questo significa proprio che f è continua in p.
Questo è un fatto molto importante, ovvero la possibilità di studiare la continuità senza fare uso della distanza (o senza nemmeno conoscerla), ma solamente conoscendo gli insiemi aperti. In topologia si studiano le trasformazioni continue fra spazi; grazie a questa dimostrazione possiamo dimenticarci il concetto di distanza e assegnare assiomaticamente gli insiemi aperti. Siamo perciò ora in grado di capire da dove nasce la definizione assiomatica citata all' inizio.
Nel prossimo articolo cominceremo a parlare della Topologia vera e propria.






1 commento
per non parlare degli approfondimenti di Umberto, in cui la matematica diventa quasi una forma di arte...
Insomma, ce n'è per tutti... forza ITDC (Infinito Teatro Del Cosmo)