Questo quiz è stato introdotto come preludio allo studio degli spazi metrici. Uno spazio metrico è un  insieme di punti (e può essere anche quello euclideo) , in cui è stata introdotta una definizione di distanza,anche chiamata metrica.Prima di continuare, mi sembra doveroso dire quali proprietà deve avere una distanza.

1) d(P1,P2)>=0 (La distanza è definita positiva!)

2)  d(P1,P2)=0)  se e solo se P1=P2

3)d(P1,P2)=d(P2,P1) (simmetria)

4)d(P1,P2)+d(P3,P4)>= d(P1,P4) diseguaglianza tringolare.

 

Nello spazio Euclideo, la distanza più  semplice, dati due punti per esempio nel piano, altro non è che la congiungente i due punti; se abbiamo poi un sistema di coordinate, possiamo trovarla facilmente (se conosciamo le coordinate dei due punti) applicando il teorema di Pitagora.

La sua definizione la conosciamo bene:

 

Questa non è la sola distanza  definibile fra due punti, potremmo dire che è la minima.Infatti Quazel ci propone un altra distanza, quella reticolare:

In realtà, è stata una nostra vecchia conoscenza ad introdurla per primo: Niente meno che Minkowski !

Essa prende il nome di distanza di Manhattan,  ed è chiamata anche geometria del taxi; le strade di  Manhattan sono un reticolo ortogonale, per cui il tassista per calcolare una distanza,visto che non può buttare giù i muri,altro non può fare  che fare la somma dei valori assoluti delle differenze fra coordinate: d1(P1,P2)=|x2-x1| + |y2-y1|. Abbiamo chiamato questa distanza d1 e presto vedremo perchè. Infatti  due distanze , quella Euclidea e quella di Manhattan si possono scrivere in un modo generico:

1. 

infatti per p=1,abbiamo d1(P1,P2)=|x2-x1| + |y2-y1| (Manhattan)

e per p =2 abbiamo:

distanza Pitagorica

Ebbene , Minkowski dimostrò in modo generico, che la 1) è sempre una distanza per p>=1, ed è chiamata distanza di Minkowski.  Vi prego di non confondere assolutamente questa distanza così specificata con quella dello spazio Minkowski della relatività ristretta,che è un'altra cosa*.

Non è finita qui. Durante  lo sviluppo dei commenti al quiz, ho inserito un altra domanda, citando la distanza:

(P1P2)=max(|x2-x1|,|y2-y1|), ovvero il valore massimo della differenza fra i valori assoluti delle due coordinate.

Questa distanza prende il nome di  distanza di Čebyšëv, conosciuta anche come distanza della scacchiera o distanza di Lagrange. Pensate al Re degli scacchi che deve raggiungere una certa posizione e capirete perchè è definita così.

Questa distanza viene indicata con ; Infatti può essere considerata una estensione di quella di Minkowski  quando p tende a infinito:

Infatti si dimostra che( anche se noi non lo faremo):

.

___________________________________________________________________________________

• La metrica di Minkowski della Relatività Ristretta,non è proprio una metrica; intanto non è definita positiva e addirittura in essa non vale la diseguaglianza triangolare, un lato di un triangolo è sempre maggiore della somma degli altri due.

Ma veniamo al quiz; si richiedeva di trovare che aspetto avessero i "cerchi" con le differenti distanze, e le loro posizioni reciproche rispetto al nostro cerchio usuale. In matematica si preferisce chiamare queste entità come "bolle".Infatti , a seconda della metrica possono cambiare forma, e diventare addirittura dei quadrati.Esse sono alla base della topologia. Definiamo pertanto bolla di centro a e raggio R, l'insieme:

{ tali che }; Chiaramente  nel piano con la distanza pitagorica le bolle sono i cerchi.

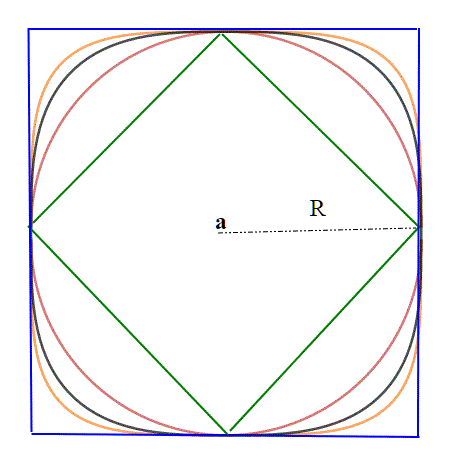
Procedendo dall'esterno verso l'interno: , d4, d3,d2 (cerchio), d1 (la distanza del quiz)

Le domande del quiz erano :

dimostrare la diseguaglianza triangolare nel caso p=1, e la forma delle bolle per d1 e .

Riporto le soluzioni dei partecipanti, che sono esaustive; ricordatevi che sono del tutto valide, anche se talvolta sono stati scelti degli assi centrati in modo particolare, essendo la distanza d1 (ma in genere ogni distanza dp) invariante per traslazioni.(Traslare le coordinate nel piano, significa aggiungere una costante; facendo la differenza questa costante viene eliminata)

Arturo, forma della bolla con p=1:

le 4 rette che vengono fuori dalla relazione che definisce la "circonferenza" di Quazel sono, in forma implicita:

x+y-R=0     (per x>0 e y>0)

-x+y-R=0   (per x<0 e y>0)

-x-y-R=0    (per x<0 e y<0)

x-y-R=0     (per x>0 e y<0)

Dette rette si intersecano a due a due nei 4 punti di coordinate (R,0), (0,R), (-R,0) e (0,-R), che sono i vertici del quadrato inscritto nella circonferenza di centro O e raggio R:

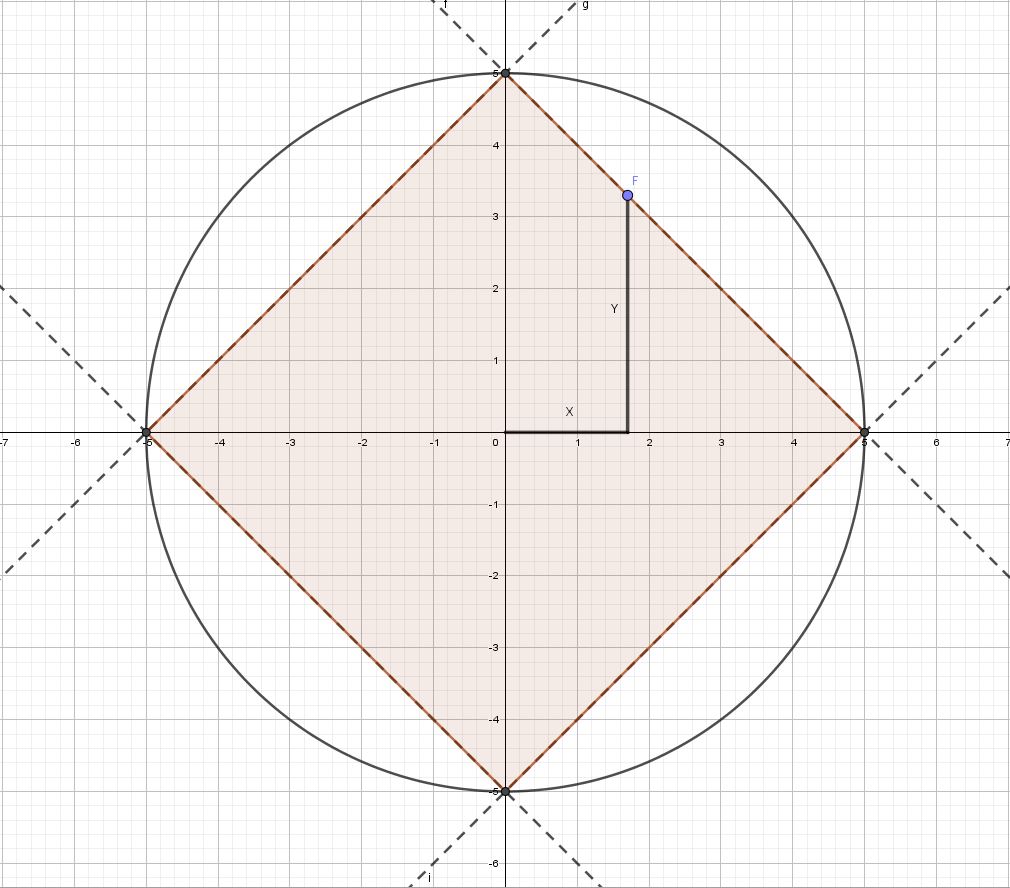
Facendo variare il punto F lungo i 4 lati del quadrato, la somma /X/+/Y/ resta costante e pari ad R.

Vincenzo, diseguaglianza triangolare per p=1:

Mi limito al primo quadrante, ma le cose non cambiano passando agli altri...

Il perimetro del triangolo OAB alieno è dato dal rettangolo di figura. La somma di due lati (ad esempio OA e OB) è per costruzione maggiore del lato AB, dato che coprono più di metà del perimetro. Identica situazione si avrebbe cambiando i lati... Se A  B fossero sugli assi y e x (caso degenere) avremmo che la loro somma sarebbe uguale al terzo lato.

La relazione decisiva è che la somma di due lati è sempre maggiore della metà del perimetro del rettangolo (triangolo alieno) e quindi è sempre maggiore del terzo lato.

 

Arturo, diseguaglianza triangolare per p=1:

Devo dimostrare che

AC < AB + BC     (1)

Suppongo che non sia vera la (1) cioe' che

AC > AB+BC      (2)

Per Quazel:

AC = AF + FC

AB = AD + DB

BC = BE + EC

Sostituendo nella (2):

AF+FC>AD+DB+BE+EC    (3)

Ma dalla figura si vede che DB+BE=AF e che FC+EC =AD quindi dalla (3):

FC>AD+EC --> FC>FC+2EC-->EC<0

il che e' impossibile. Quindi la (1) deve essere vera.

Pero' mi pare che se i tre punti A, B, C sono i vertici di un triangolo rettangolo isoscele con ipotenusa inclinata di 45 gradi rispetto all'asse x, la distanza AC sara' proprio pari alla somma AB+BC, quindi la (1) e' vera ma non sempre.

(Si, la diseguaglianza triangolare è da interdersi con il >=, anche se con la distanza Pitagorica vale sempre il >.

Maurizio, forma della bolla nella metrica del max:

La distanza è definita come il valore massimo tra la componente orizzontale e la componente verticale

Fisso il raggio = modulo (x2-x1)  e il centro (x1,y1)

il  "cerchio" è il quadrato circoscritto al cerchio (euclideo) di raggio   e centro x1,y1.

Immagino il raggio che esce dal centro x1,y1 e interseca il "cerchio" quadrato, e lo osservo ruotare: finché non arriva ai 45° la distanza è la proiezione orizzontale, sulle x, maggiore della proiezione verticale, sulle y. In corrispondenza ai 45° le due proiezioni sono uguali,  oltre ai 45° la situazione si inverte e la componente verticale è quella massima, fino a 135° ,  e così via fino a completare il giro.