Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Premessa storica

Nei primi anni del 1900 Poincarè stava costruendo la topologia algebrica, in particolare sviluppò un strumento chiamato omologia  che gli permise di classificare le varietà di dimensione due. Estese le omologie anche alle varietà di dimensione 3 ma si accorse che tale strumento non  era quello più appropriato. Non parleremo  delle omologie, sia perchè sono tecnicamente difficili, sia perchè si dimostrarono non completamente efficaci. Poncarè trovò un altro sistema per classificare le varietà; le omotopie e il gruppo fondamentale. Di questo parleremo in questo primo articolo.

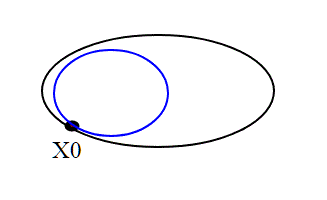
Le omotopie (dal greco homos = identico e topos = luogo)  serviranno per introdurre il concetto di gruppo fondamentale e di  semplice connessione. L'idea intuitiva,per esplorare le superfici e le varietà topologiche, è di partire da un punto e tornare in esso stendendo una corda.Pensiamo di fissare la corda con un chiodo e di andare in giro per la superficie srotolando la corda. Dopodichè tornare al chiodo e cercare di riavvolgere la corda, tenendo sempre legato l'altro estremo al chiodo. Se questo è sempre possibile,qualsiasi sia il punto da dove si parte e qualsiasi sia il percorso, diremo che la superficie è semplicemente connessa.   Abbiamo due esempi lampanti di superfici dove questo si possa o non si possa fare; la sfera e il toro:

 

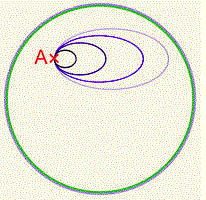
Intuitivamente, la semplice connessione ci fa capire se la varietà "ha buchi" o no.

Questo fu proprio il punto di partenza di Poincaré per classificare le varietà topologiche. Per formalizzare la semplice connessione abbiamo bisogno di un concetto importante:

L'OMOTOPIA

Date due applicazioni continue , dove X,Y sono due spazi topologici diremo intuitivamente che f0,f1 sono omotope  se f1 si ottiene per deformazione continua da f0:

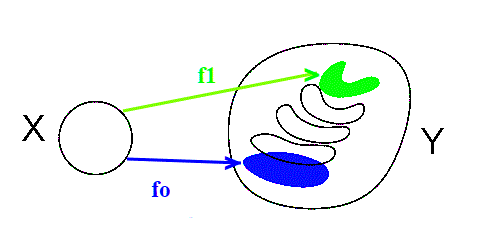
detto formalmente, e indicando con    ,  si dicono omotope se esiste una funzione continua,   tale che  per ogni   si abbia:

F(x,0)=f0(x);  F(x,1)=f1(x) .

Per indicare che f0,f1 sono omotope scriveremo . Se poi poniamo  avremo una famiglia di funzioni dipendenti dal parametro  che variano con continuità do f0 a f1.

Facciamo subito un esempio; se ,ovvero il disco piano, consideriamo come f0 l'identità su , ovvero la funzione che manda ogni punto in se stesso. Mentre per f1 la funzione costante , f1=0. Se consideriamo la funzione , essa realizza un omotopia tra f0 e f1. Infatti f0(x)=(1-0)x=x che è l'identità. Mentre f1(x)=(1-1)x=0.

 

IL GRUPPO FONDAMENTALE  

In uno degli articoli della vecchia serie, abbiamo trattato la connessione per archi,  di conseguenza  abbiamo introdotto il concetto di arco:

Sia X uno spazio topologico.Consideriamo l'intervallo [0,1]. Sia f:[0,1]--->X una funzione continua. Tale funzione prende il nome di arco su  X(è una linea continua contenuta in X). L'arco viene anche chiamato cammino. Ricordiamo anche la definizione di connessione per archi:

Diciamo che il nostro spazio X è connesso per archi, se comunque scegliamo due punti a,b esiste un arco f tale che f(o)=a,f(1)=b. Noi tratteremo d'ora in poi spazi connessi per archi.

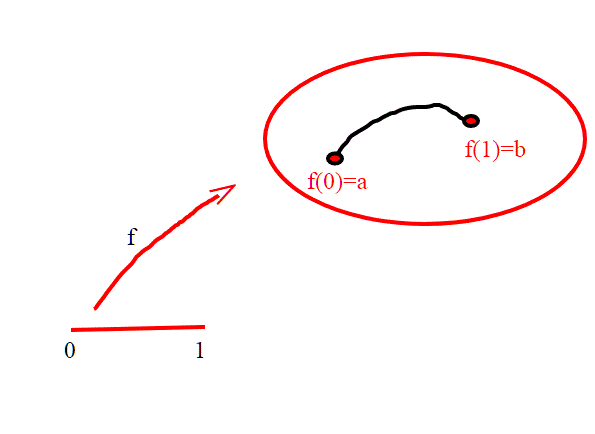
f(0) viene anche chiamato punto iniziale, e f(1) punto finale (del cammino).Se f(0)=f(1) allora il cammino diventa un cammino chiuso, e viene anche chiamato cappio. Diremo ancora più precisamente, se , che è un cappio di punto base x0.

 

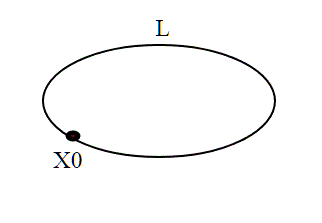
Consideriamo adesso l'insieme dei cappi (base x0) che sono omotopi. Essere omotopi è una relazione d'equivalenza. Chiamiamo  l'insieme quoziente di tale relazione d'equivalenza. Intuitivamente (come abbiamo visto sopra per la corda) questo insieme dovrà darci delle informazioni sulla struttura della spazio X; vogliamo definire sull'insieme   una operazione interna.  Trattandosi di applicazioni, la cosa più naturale è pensare alla composizione:

siano 

definiamo: 

questa operazione è ben definita, ovvero non dipende dai rappresentati scelti per le due classi.

 

Si dimostra (noi non lo faremo) che con questa operazione   diventa un gruppo, ossia soddisfa alle tre proprietà:

1. proprietà associativa
2. esistenza elemento neutro
3. esistenza dell'inverso per ogni elemento.

il gruppo  prende il nome di GRUPPO FONDAMENTALE di X ed è uno degli oggetti più affascinanti della topologia algebrica. Esso dà  informazioni su come è fatto lo spazio topologico X, senza pensare a dove sia immerso.

(a scanso di equivoci, il gruppo fondamentale in uno spazio connesso per archi non dipende dal punto scelto; se infatti x0,yo sono due punti dello spazio X e se esiste un arco f che congiunge x0 con y0, allora si dimostra che . Essendo per ipotesi X connesso per archi, questo vale qualsiasi siano i due punti.)

Perchè costruire i gruppi fondamentali di un insieme topologico?

Quello che interessa di più in topologia, è vedere se due spazi sono omeomorfi. Spesso però questo è difficile; si prova perciò a confrontare i rispettivi gruppi fondamentali; se sono isomorfi, allora i due spazi sono omeomorfi. Ricordo che due gruppi sono isomorfi se esiste una corrispondenza biunivoca fra i due che conserva le operazioni. Per il matematico due gruppi isomorfi sono algebricamente lo stesso oggetto, come lo sono due spazi topologici omeomorfi. Per trovare il gruppo fondamentale dobbiamo trovare tutte le classi di equivalenza dell'insieme quoziente . Dobbiamo ragionare dunque sui cappi omotopi.

Due esempi molto significativi.

Ma vediamo degli esempi; trovare qual'è il gruppo fondamentale della circonferenza o del toro non è effettivamente la cosa più semplice di questo mondo. Noi procederemo per intuizione. Cominciamo dalla circonferenza.

 

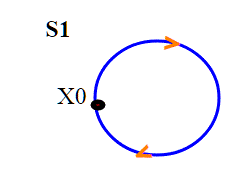
Il nostro insieme X consiste dunque in una circonferenza. I cappi, dovendo stare su di essa, sono rappresentati da degli archi.  I cappi sono degli archi che fanno uno o più  giri completi della circonferenza, partendo da X0 e tornando in X0. Essi non sono riducibili ad un punto, e non sono fra di loro omotopi. Il cappio costante corrisponde invece a zero giri.  Quindi le classi di equivalenza rispetto all'omotopia sono tante quanti i numeri interi (possiamo girare in senso orario o antiorario). Concludiamo dicendo che il gruppo fondamentale della circonferenza è Z, anzi è isomorfo a Z.

 

Per quanto riguarda il toro,il cappio C del disegno  può ridursi con continuità ad un punto. Non ci dà quindi  nessuna informazione sui possibili buchi.

 

 

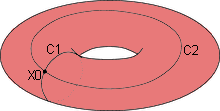
I cappi C1 e C2 non possono ridursi ad un punto; entrambi individuano il buco nel toro.  Trovare il gruppo fondamentale del toro significa trovare tutte le classi di equivalenza della relazione di omotopia. Se partiamo dal cappio C1, ad ogni giro successivo avremmo un cappio non omotopo al precedente.  Questo vale anche per C2. Se poi componiamo due qualsiasi di questi cappi, otteniamo un terzo cappio, che non è omotopo a nessuno dei due. Quindi avremo in totale Z x Z classi di equivalenza distinte. Possiamo dire che il gruppo fondamentale del toro è omeomorfo a Z x Z.

 

La connessione semplice

Eccoci arrivati  al dunque;  fra tutti i gruppi  consideriamo  quello banale, che consta di un solo elemento. Diremo che uno spazio X è semplicemente connesso se il suo gruppo fondamentale è il gruppo banale.Il gruppo banale consta dunque di un solo elemento. Se chiamiamo e tale elemento, esso deve essere sia l'inverso di se stesso e sia l'elemento neutro del gruppo.Questo elemento altro non può essere che il cappio costante, ovvero  un punto.Sappiamo che per trovare il gruppo fondamentale di X dobbiamo considerare un punto X0 su X e trovare le classi di equivalenza dei cappi rispetto alla omotopia.Quindi dobbiamo considerare i cappi omotopi con punto base X0.  Se tutti i cappi si riducono a un punto, allora X è semplicemente connesso.Per quanto visto sopra nella definizione di gruppo fondamentale, questo deve valere  per qualsiasi altro punto Y0 diverso da X0.

La sfera è semplicemente connessa , mentre il toro non lo è:

Nel toro non tutti i cappi si riducono ad un punto (come abbiamo visto sopra). Mentre nella sfera si, qualsiasi sia il punto A. Nel toro infatti il gruppo fondamentale è il gruppo Z x Z, che non è il gruppo banale.

Avremmo potuto parlare di semplice connessione  senza parlare di gruppo fondamentale, ma questo è il percorso storico che fece arrivare Poincarè alla congettura. Avremmo cioè potuto dare la definizione più in uso che riassume i discorsi fatti sopra:

Uno spazio topologico si dice semplicemente connesso se è connesso per archi e ogni curva chiusa giacente su di esso può essere deformata fino a ridursi a un singolo punto.

Ma da dove ha origine il termine "semplice connessione"?

Perchè "semplice connessione"?

Ricordo che una curva semplice chiusa è in pratica una curva che non ha auto-intersezioni. Ogni curva semplice chiusa è omeomorfa chiaramente alla circonferenza.

Curva chiusa semplice	Curva chiusa intrecciata

 

Si dice che una curva chiusa semplice C appartenente ad una superficie S separa  S se S\C non è connesso, ovvero la superficie viene tagliata in due pezzi da C.

 

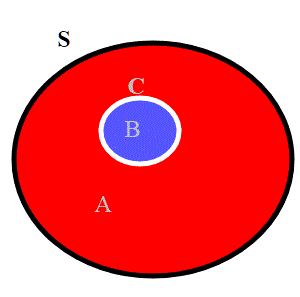
Da questo concetto deriva la terminologia "semplicemente connesso".  La sfera è connessa in modo più semplice del toro, in quanto la prima si riesce a separare con una curva chiusa semplice , mentre non è possibile separare il secondo con una sola curva chiusa semplice.
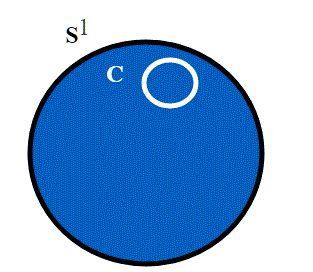