Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nell'ultimo articolo di questa serie abbiamo parlato di spazi connessi. Ricordo le due definizioni più importanti di connessione, che ci serviranno subito.

Due definizioni equivalenti di connessione.

Sia X un insieme: X è connesso se:

1) Non esistono due aperti che siano non vuoti, disgiunti e tali che la loro unione dia tutto X.

2)  Non esistono due chiusi che siano non vuoti, disgiunti e tali che la loro unione dia tutto X.

Continuiamo il discorso sugli spazi connessi, introducendo le componenti connesse e la connessione per archi.

Una osservazione importante:

Siano Y e Z connessi in uno spazio topologico X. Se Y Ç Z ¹ Æ, allora Y È Z è connesso.

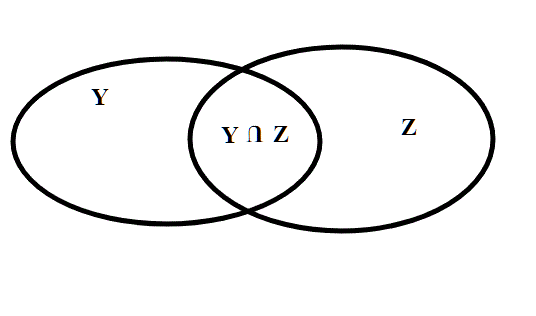
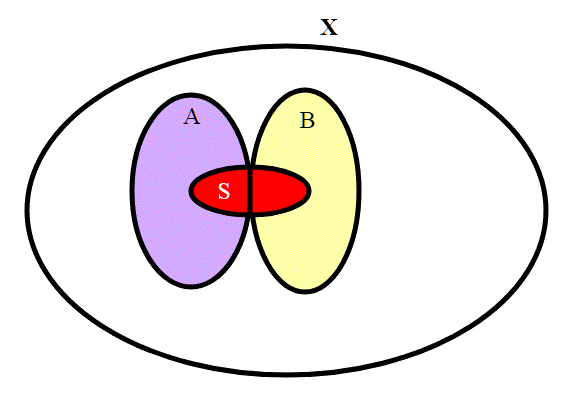
Facciamo una premessa:      sia S un sottoinsieme connesso di X, e supponiamo  con A e B aperti non vuoti e disgiunti, allora S   A oppure S  B infatti, se non fosse così, potremmo scrivere ) unione di aperti in S non vuoti e disgiunti che implica che S  è sconnesso; quindi vale oppure, da cui oppure , che è possibile solo se   S   A oppure S  B

Torniamo alla proposizione:

Siano Y e Z connessi in uno spazio topologico X. Se Y Ç Z ¹ Æ, allora Y È Z è connesso.

Assumiamo per assurdo che esistano A, B aperti, non vuoti, disgiunti tali che . Questa uguaglianza comporta che   e che .

Per ipotesi Y  è connesso, quindi Y  A oppure Y B, (osservazione precedente) questo vale anche per Z, inoltre si esclude che Y  Z sia contenuto completamente in A (oppure in B) perché in tal caso B (oppure A) sarebbe vuoto; quindi non perdiamo di generalità assumendo Y A e Z B   che implica che   A  B  Y   Z, ma sappiamo che  . 

Componenti connesse

Se consideriamo l'iperbole nel piano come sottospazio topologico, vediamo che è sconnessa:

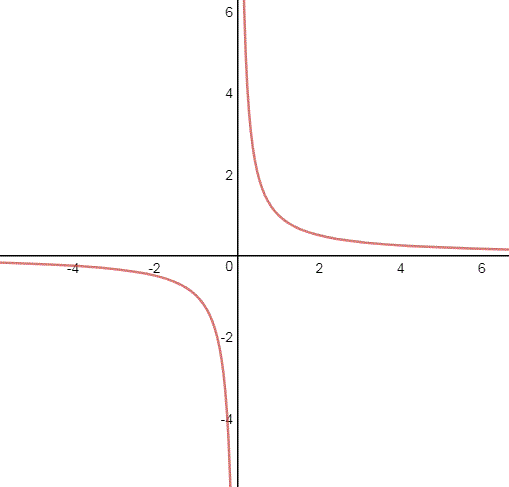
I due rami sono invece connessi . Chiaramente i due rami sono disgiunti, e la loro unione dà l'iperbole. I due rami prendono il nome di componenti connesse. Ciò risulta molto intuitivo. Ma vediamo come si arriva alla definizione formale di componenti connesse.

In uno spazio topologico X, due punti x e y sono detti connessi se $ un  connesso Y tale che x, y Î Y.

La relazione r definita su uno spazio topologico X da: "" x, y Î X, xr y Û x e y sono connessi in X" è una relazione di equivalenza :

i) x  x;  infatti basta considerare un connesso che contiene x,

ii) se x  y, allora y  x  se esiste un connesso che contiene x e y, questo contiene anche y e x

iii) se  x  y e  y  z  allora esiste un connesso C che  contiene  x,y e un connesso C' che contiene y,z; ma allora C e C' hanno un punto in comune, y, pertanto ; ma allora , come dimostrato sopra, C U C'è connesso e contiene x, z  quindi x  z

Ma una relazione di equivalenza induce una partizione di X:

Ogni spazio topologico X è unione disgiunta delle sue componenti connesse.

1. L’iperbole in R2 ha 2 componenti connesse, ovvero i due rami, ciascuna dei quali omeomorfo a R.
2. X = [0, 1] ∪ [2, 3] ha due componenti connesse: [0, 1] e [2, 3]

Connessione per archi; un piccolo cenno.

Un altro sistema per verificare la connessione di uno spazio topologico è la seguente.

Sia X uno spazio topologico.Consideriamo l'intervallo [0,1]. Sia f:[0,1]--->X una funzione continua. Tale funzione prende il nome di arco su  X(è una linea continua contenuta in X).

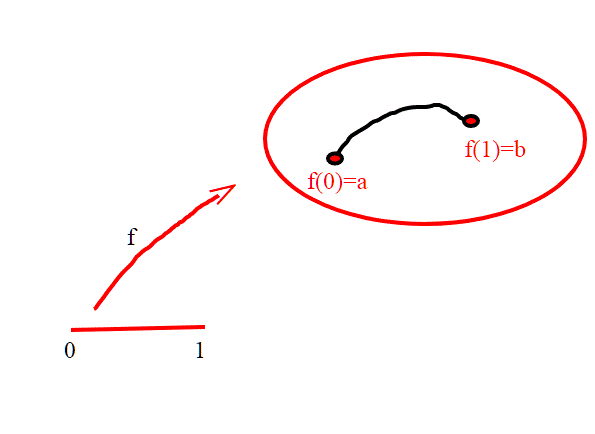
Diciamo che il nostro spazio X è connesso per archi, se comunque scegliamo due punti a,b esiste un arco f tale che f(o)=a,f(1)=b. Uno spazio connesso per archi è connesso:

Assumiamo per assurdo che X = A  U B con A, B aperti non vuoti, disgiunti, allora prendiamo aA e b B; per ipotesi esiste un arco a che li congiunge:

f : [0, 1] ---> X tale che f(0) = a, f(1) = b; I = [0, 1] è connesso quindi  f(I) connesso,

sarebbe unione di aperti non vuoti e disgiunti, quindi sconnesso: assurdo.

Non è però vero il viceversa; ci vuole un controesempio e ne esiste uno molto complesso, detto il seno del topologo,

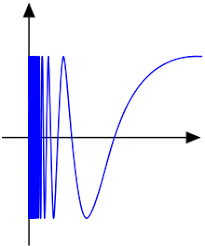
chissà forse un giorno potremmo provare a  dimostrarlo per esercizio,cercando di approfondire meglio.

Chiudiamo qui con la connessione: la prossima volta affronteremo concetti più avanzati che ci porteranno a definire dei sottospazi importanti, fra i quali il nastro di Möbius. Sto parlando di topologia quoziente.