Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Introduzione.

Abbiamo visto che gli omeomorfismi sono un sistema per verificare se due spazi sono topologicamente equivalenti. A volte è un po' difficile però decidere se esiste o no un omemorfismo fra due spazi, perciò si è costretti a ricorrere ad altri metodi. Siamo alla ricerca di una proprietà che contraddistingua gli spazi e che resti tale se le si applica un omeomorfismo.

Una di queste proprietà è la connessione.

Insiemi chiusi.

Ricordo che per definire una topologia, dobbiamo dare un famiglia di insiemi, detti aperti. Se X è l'insieme dei punti dello spazio topologico, Un sottoinsieme di X, C, si dice chiuso se il suo complementare A  in X è aperto; partendo dalla topologia di uno spazio metrico come , proviamo a capire il senso di questa definizione.

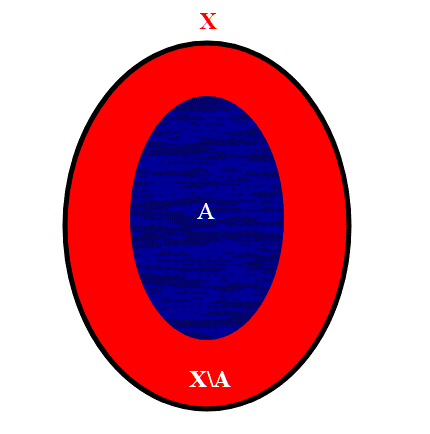
Quando abbiamo parlato degli aperti negli spazi metrici, qui, avevamo visto in particolare che:

1.  (insieme vuoto) e X sono aperti

 non ha punti,quindi è aperto;  prendiamo un qualsiasi punto x di X; qualsiasi bolla con centro in X è per forza contenuta in X , basta vedere la definizione di bolla;{ tali che }

Ma allora se  è aperto, il suo complementare X è chiuso; allo stesso modo essendo X aperto, il suo complementare  è chiuso. Capiamo allora che un insieme può essere contemporaneamente  aperto e chiuso, una cosa non esclude l'altra.

Dalle proprietà degli aperti, si deducono delle analoghe proprietà per i chiusi:

i)  (insieme vuoto) e X sono chiusi

(lo abbiamo appena visto)

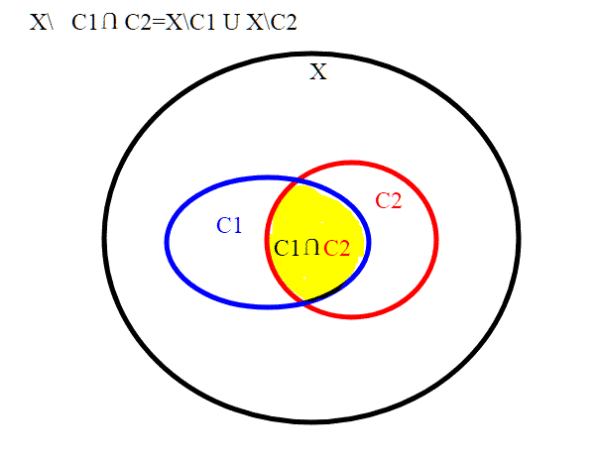
ii)l'intersezione di una famiglia di insieme chiusi, Ci ,è un insieme chiuso:

sappiamo che X \ = (X \ C_i)  risulta essere un aperto, quindi l’intersezione sarà un chiuso.

Vediamo la validità di questa eguaglianza  graficamente nel caso di due insiemi C1,C2

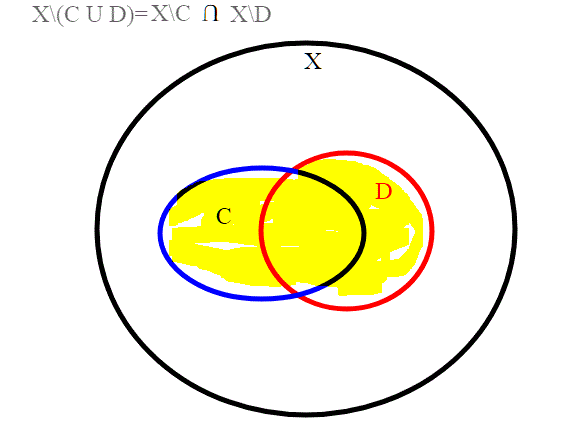
iii) se C e D sono chiusi, anche C U D è chiuso.

essendo X\C U D)=(X\C)  (X\D)  che risulta un aperto, quindi l’unione sarà un chiuso.

Definizione di connessione.

Uno spazio topologico X si dice connesso se gli unici sottoinsiemi di X che sono sia aperti che chiusi sono X e ∅. Viceversa, uno spazio topologico X che ha un sottoinsieme contemporaneamente aperto e chiuso, diverso da X e da ∅, si dice sconnesso. L'idea intuitiva di uno spazio connesso è quella di "spazio fatto di un unico pezzo ".

 

Lo spazio R  della retta reale è connesso.

Non dimostreremo questo fatto, perchè la dimostrazione implica delle conoscenze di analisi matematica che non tutti possono avere.

Intuitivamente, è una conseguenza della continuità dei numeri reali; sappiamo che nella retta reale non ci sono "buchi".

 

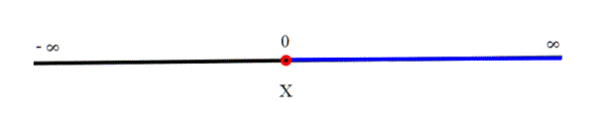
Se consideriamo la retta R, che  è connessa, e gli togliamo un punto, ad esempio  lo zero, otteniamo un insieme X = R − {0} che risulta sconnesso.infatti D=(−∞, 0) è un sottoinsieme di X che è sia aperto che chiuso. Per vedere questo osserviamo che (−∞, 0)= X ∩ (-∞, 0], quindi è chiuso * (intersezione di chiusi) e (−∞, 0) = X ∩ (-∞, 0) e quindi è aperto (intersezione di aperti). Quindi D è sia aperto che chiuso.

*Teniamo presente che X è sia chiuso che aperto.

Definizioni equivalenti di connessione.

Esistono altre due definizioni di connessione, equivalenti a quella data.

1) Non esistono due aperti che siano non vuoti, disgiunti e tali che la loro unione dia tutto X.

2)  Non esistono due chiusi che siano non vuoti, disgiunti e tali che la loro unione dia tutto X.

Intanto vediamo che 1,2 sono equivalenti.

supponiamo  (per assurdo)che esistano A, B aperti non vuoti e disgiunti, la cui unione è X, vogliamo vedere che in questo modo esistono C, D chiusi non vuoti e disgiunti la cui unione sia X; basta prendere C = B = X \ A è il complementare di un aperto e quindi è chiuso;  e D = A=X\B che è sempre il complementare di un aperto, quindi è chiuso; D U C dà poi proprio X.

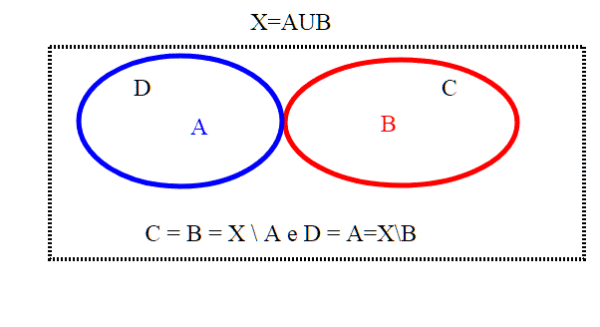
Riprendiamo adesso la prima definizione di spazio connesso che abbiamo visto per prima:

Uno spazio topologico X si dice connesso se gli unici sottoinsiemi di X che sono sia aperti che chiusi sono X e ∅.

dimostriamo che questa definizione è equivalente alla 1)

esistono A, B aperti non vuoti e disgiunti tali che A U B = X ; A è aperto e B = X \ A aperto se e solo se A è chiuso. Quindi A è sia aperto che chiuso.

Ci serve adesso un criterio per poter dire se uno spazio è connesso o no, basandoci sulla connessione di spazi che conosciamo (ad esempio proprio R). Ci viene in aiuto questo teorema, che possiamo provare a dimostrare:

Se f : X → Y `e una funzione continua tra due spazi topologici e X è connesso, allora anche f(X) è connesso.

Possiamo supporre f suriettiva. f : X--->Y. In tal caso Y prende il ruolo di f(X). Per assurdo scriviamo,  se Y non è connesso, Y = A    B con A e B aperti non vuoti e disgiunti;

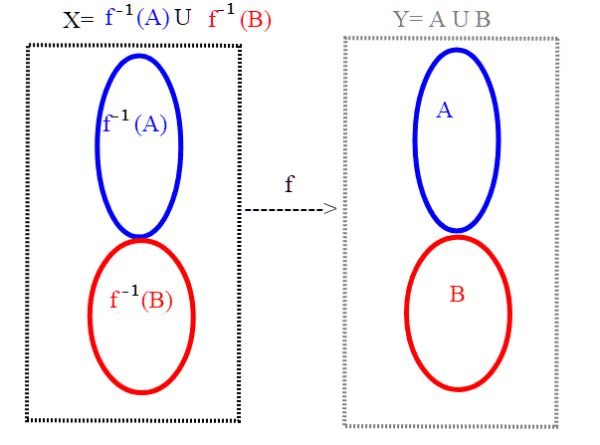
Vediamo che  ; infatti chiaramente ; dobbiamo dimostrare che . Sia x un qualsiasi  ; allora f(x)=y appartiene a Y = A    B. Questo significa che y appartiene ad A o y appartiene a B. Ma allora  o .

Abbiamo poi che . Infatti se per assurdo  , essendo , , avremmo un , contro l'ipotesi che siano disgiunti.

Dunque f ^–1 (A) e f ^–1 (B) sono aperti (per la  definizione di continuità), non vuoti e disgiunti quindi  X è sconnesso. Assurdo.

Ma se abbiamo a che fare con un omeomorfismo la funzione f ,continua, è senz'altro suriettiva su  Y. Se ne conclude che  se esiste un omeomorfismo di X-->Y , X è connesso se e solo se Y è connesso. Infatti la f è continua e suriettiva ed anche la sua inversa  lo è per definizione di omeomorfismo. quindi il discorso vale in entrambi i sensi. Ritorniamo dunque al discorso  fatto nell'introduzione: abbiamo trovato un metodo alternativo per vedere se due spazi sono omeomorfi. Infatti, se X è connesso e Y no, non possono essere due spazi omeomorfi, quindi inutile cercare un omeomorfismo.

Teniamo presente adesso gli esempi di omeomorfismo fatti qui.

L’intervallo [−1, 1] è connesso, essendo l’immagine di R tramite la funzione f(t) = sin t, di conseguenza anche ogni

intervallo di tipo [a, b] è  connesso essendo omeomorfo a [−1, 1]. (  sappiamo che un omeomorfismo può “allungare” o “accorciare” a piacere un segmento.)

 

Si può dimostrare che i sottoinsiemi di R connessi sono tutti e soli gli intervalli.
Il cerchio S1 (cerchio di raggio unitario) `e connesso, essendo immagine della funzione continua f :   data da f(t) = (cos t, sin t).

 

La prossima volta parleremo di un altro modo per definire la connessione (connessione per archi) e delle componenti connesse.