Vorrei cambiare un po' metodo di stesura degli articoli, e farne tanti di piccole dimensioni , su cose semplici, ma che magari sfuggono alla conoscenza della maggior parte dei lettori. Non mi sono dimenticato della serie su Poincarè, ma l'articolo che sto preparando sulla connessione fra metrica e curvatura è impegnativo, e richiede molto tempo. Introduco questo argomento per proseguire con la teoria di Ramsey, come anticipato nell'ultimo quiz. Questo principio ci servirà infatti fra poco. Scusate il nome provvisorio del principio, un pò macabro, ma attualmente è quello che mi viene in mente attualmente.

Stiamo comunque parlando  del più noto "Principio dei cassetti"

Il Principio dei cassetti (in inglese Pigeonhole Principle, "principio della piccionaia") afferma un fatto abbastanza ovvio": n + 1 buste non possono essere collocate in n cassetti in modo che ogni  cassetto contenga una sola busta.

Detto in termini di piccioni o colombi: se n+1 piccioni volano in una piccionaia con n buche, in almeno una buca
finiranno due o più piccioni.

Detto in modo formale: non esistono applicazioni iniettive da un insieme di n+1 elementi in uno di n elementi.

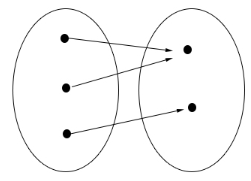
In realtà, il principio dei cassetti non è un principio, ma un teorema vero e proprio.

Possiamo dare infatti una piccola dimostrazione:

Per assurdo, se ogni contenitore contenesse solo un oggetto, si avrebbe che il numero totale di oggetti sarebbe solo n. Ma noi abbiamo supposto che tale numero sia n + 1.

Possiamo anche dimostralo per induzione:

non possiamo collocare n+1 oggetti in n contenitori.

Per n=1 è vero. Infatti abbiamo due oggetti e un unico contenitore. Supposto vero per n, dobbiamo dimostrarlo per n +1.

Dunque; per ipotesi induttiva, non riusciamo a collocare n+1 oggetti i n contenitori. Aggiungiamo un oggetto agli n+1 , quindi passiamo da n a n+1 per quanto riguarda l'induzione. Gli oggetti diventano n+2, e le buche n+1. Possiamo mettere l'oggetto aggiunto solo nel nuovo contenitore, ma per ipotesi induttiva più di un oggetto è già nello stesso contenitore .

Notiamo che  il principio  non dà indicazioni su quale contenitore abbia più di un oggetto. L'unica cosa che possiamo affermare con certezza è l'esistenza di un tale contenitore.

Esiste una forma  più forte del principio dei cassetti, ma la vedremo in un altro articolo.

La prima formulazione ufficiale di tale principio è dovuta a Dirichlet nel 1834 col nome Schubfachprinzip
("principio del cassetto"). Per questo motivo tale principio è anche noto come principio di Dirichlet.  Vediamo attraverso degli esempi,  come un principio talmente banale, possa portare ad affermazioni a prima vista sconcertanti.

A Roma ci sono due persone (non calve) che hanno lo stesso numero di capelli.
Il numero di capelli di un essere umano è sicuramente inferiore a 500.000. Poiché a Roma risiede più di un milione di persone,segue che ce ne devono essere almeno due con lo stesso numero di capelli.

Due o più persone che partecipano al nostro  circolo hanno lo stesso compleanno.

Ci sono 366 possibili compleanni (incluso il 29 febbraio in un anno bisestile) e questo blog ha molti più di 367 lettori. Pertanto, due di essi  devono avere lo stesso compleanno.

Una persona possiede n paia di identici guanti di lana, ogni paio di un colore diverso. Quanti
guanti deve prendere come minimo, al buio, per essere sicuro di aver selezionato almeno un paio di guanti
dello stesso colore?

Prendendo n guanti, non può avere la certezza di un paio completo (potrebbero essere tutti di colore
diverso). Con n + 1 guanti, ce ne devono essere due dello stesso colore.

Questi esempi sono classici e sono  stati trovati  nella letteratura matematica; vi lancio una sfida creativa (per questo ho messo anche il tag QUIZ):

Senza cercare da nessuna parte sareste in grado di inventare di sana pianta degli esempi di questo tipo? Così li aggiungiamo all'articolo come patrimonio personale del circolo.