In ricordo di Umberto Cibien, prematuramente scomparso, riproponiamo alcuni dei suoi migliori articoli.

Adesso che abbiamo introdotto il concetto di insieme, vediamo come legare fra loro due insiemi. Introduciamo il concetto di corrispondenza fra due insiemi con un esempio. Chiamo R l'insieme delle regioni italiane  e C l'insieme delle città italiane. Definisco una corrispondenza fra R e C in questo modo: associo ad ogni regione le proprie città:

 

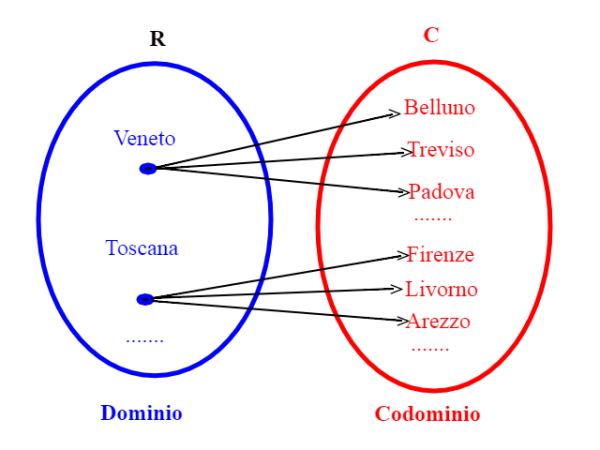
Si ha una corrispondenza quando sono assegnati un insieme di partenza, detto dominio, un insieme di arrivo, detto codominio, e un insieme di collegamenti (che possiamo pensare come delle frecce) che uniscono elementi del dominio con elementi del codominio.

In questo esempio abbiamo visto che ad un elemento del dominio possono anche
corrispondere più elementi del codominio. Si dice anche che la corrispondenza non è univoca.
Le corrispondenze univoche, sono invece quelle corrispondenze in cui ad ogni elemento del dominio viene associato al più un elemento del codominio. Una corrispondenza univoca è anche detta funzione.
Si dice funzione di A in B una corrispondenza univoca f tra gli insiemi A e B, cioè una corrispondenza che associ ad ogni elemento di A un solo elemento di B. Le funzioni si indicano di solito in questo modo:

f:  A---> B

Nell'esempio precedente, se restringiamo l'insieme C delle città a quello dei capoluoghi di regione, otteniamo una corrispondenza univoca (ovvero uno funzione):

 

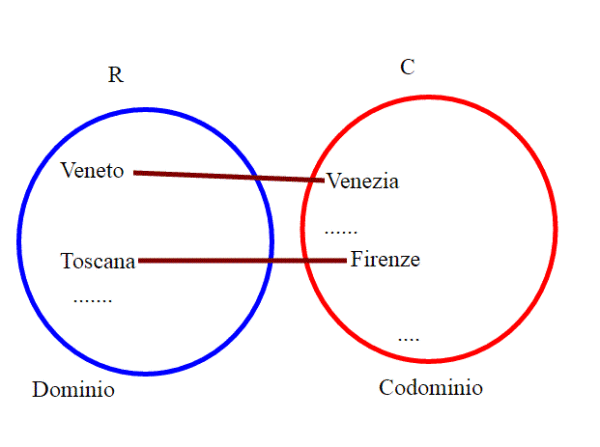
Partendo dalle corrispondenze, abbiamo ottenuto un altro oggetto matematico che è la funzione. Andiamo ad analizzare due importanti  proprietà delle funzioni. In generale una funzione manda un elemento del dominio in un solo elemento del codominio.

Immagine di un elemento del dominio.

Data una funzione f : A---> B, chiamiamo immagine  di un elemento x del dominio A l'elemento f(x) che appartiene al codominio B. Chiamiamo invece immagine di A e lo indichiamo con f(A) l'insieme costituito da tutti gli f(x), con x che appartiene ad A.

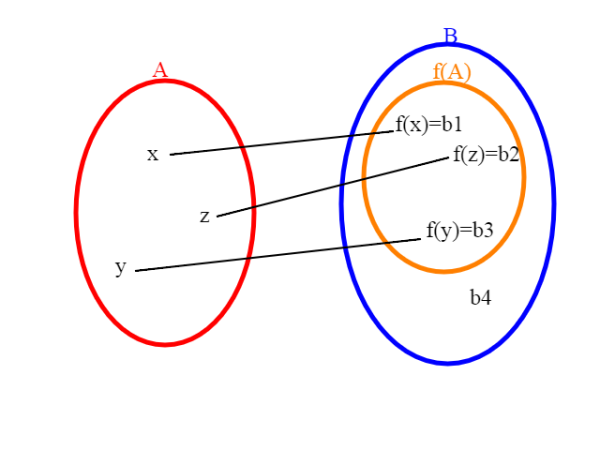
A={x,y,z} , B={b1,b2,b3,b4}; f(x)=b1 (l'immagine  di x è b1) f(y)=b3 (l'immagine  di y è b3) f(z)=b2 (l'immagine  di z è b2).

f(A) (immagine dell'insieme A) è f(A)={f(x),f(y),f(z)}={b1,b3,b2}

 

Funzione iniettiva

Una funzione è iniettiva quando manda elementi distinti del dominio in elementi distinti del codominio.

Procediamo con degli esempi. Consideriamo le città e le regioni, ed associamo ad ogni città la propria regione.

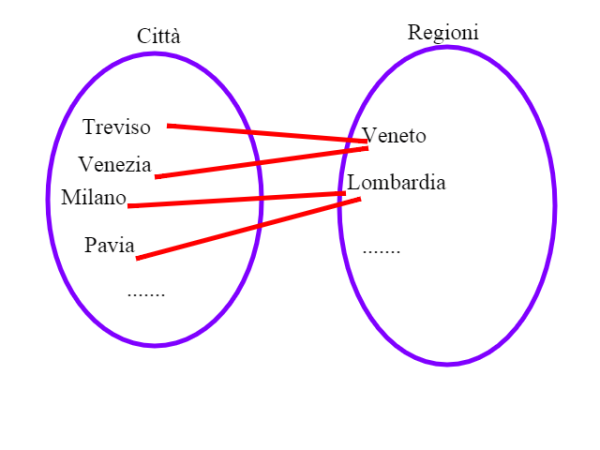
questa non è una funzione iniettiva, in quanto una regione ha più città.

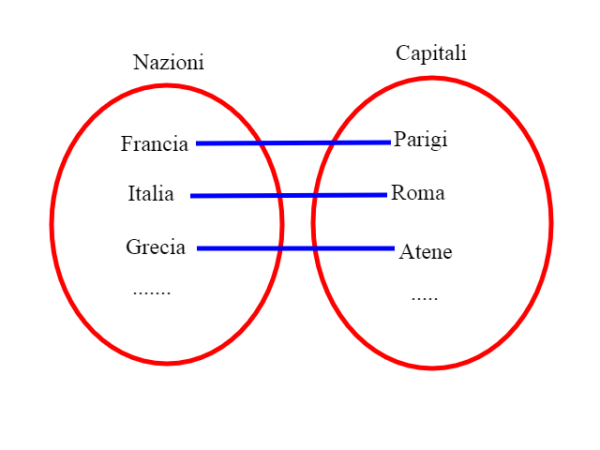
Mentre  se associamo uno stato con la sua capitale abbiamo una funzione iniettiva, in quanto per stati diversi abbiamo capitali diverse.

Funzione suriettiva.

Come sappiamo, per definire una funzione, a parte la legge di corrispondenza, servono due insiemi A e B, detti dominio e codominio. La funzione f : A-->B si dice suriettiva se tutti gli elementi di B sono immagine di qualche elemento di A. In parole povere f copre tutto B.

 

 

 

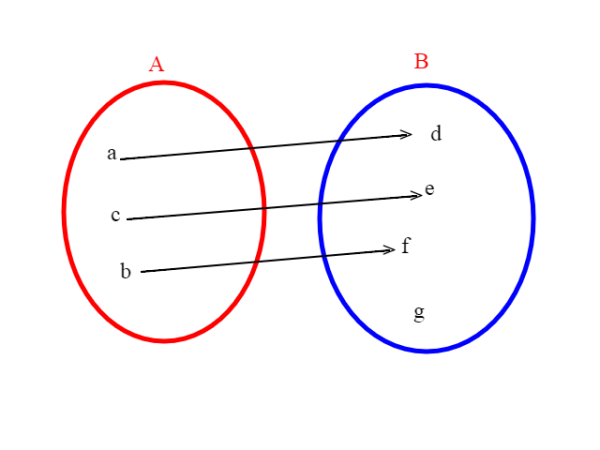
Questa sopra NON è una funzione suriettiva, in quanto l'elemento g di B non è immagine di alcun elemento di A.

Questa funzione invece è suriettiva in quanto copre tutto B (anche se non è iniettiva):

 

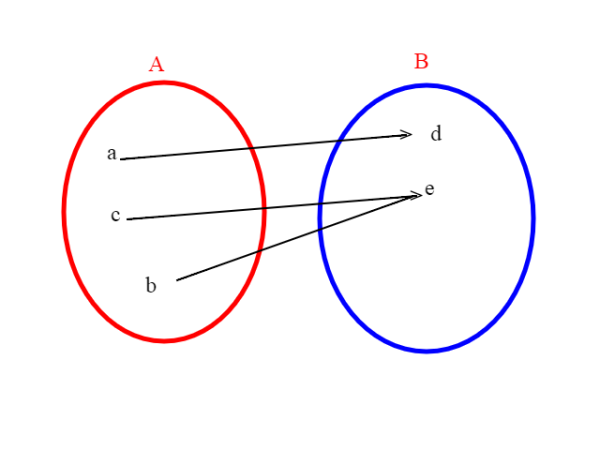
Ricordando la definizione di immagine di un insieme tramite una funzione f, si può anche dire che f è suriettiva se f(A) coincide con il codominio B.

Funzioni biettive.

Una funzione si dice biettiva se è iniettiva e anche suriettiva. Possiamo anche dire che in tal caso esiste una corrispondenza biunivoca fra dominio e codominio. L'esempio di Nazioni e Capitali è una corrispondenza biunivoca.

Una corrispondenza biunivoca è fondamentale per definire la cardinalità di un insieme (o meglio, definire quando due insiemi hanno lo stesso numero di elementi).

Infatti possiamo dire che due insiemi hanno lo stesso numero di elementi (senza preoccuparci quale sia tale numero) se possono essere messi in corrispondenza biunivoca.

Esempi di corrispondenze biunivoche con insiemi numerici

Se consideriamo l'insieme dei numeri naturali N={0,1,2,3,4,5,....}

e l'insieme dei numeri pari P={0,2,4,6,8,10....}

consideriamo la funzione f: N---> P così definita:

f(n)=2 n :dimostriamo che è una funzione iniettiva .

 

Infatti se   e moltiplico a destra e sinistra per 2 ottengo    ma :

 ,  (sono le rispettive immagini di n1 ,n2 quindi   quindi la funzione manda elementi distinti in elementi distinti.

é anche suriettiva: infatti dato un qualsiasi numero pari p, esso è divisibile per 2, quindi p si può scrivere come p=2*n, ma allora p=f(n). Quindi f è biettiva, ovvero è una corrispondenza biunivoca.

Notiamo una cosa importante; i due insiemi N, P sono degli insiemi infiniti (non riusciamo infatti a contare gli elementi dei due insiemi) e addirittura  P è contenuto strettamente in N , però riusciamo a metterli in corrispondenza biunivoca.

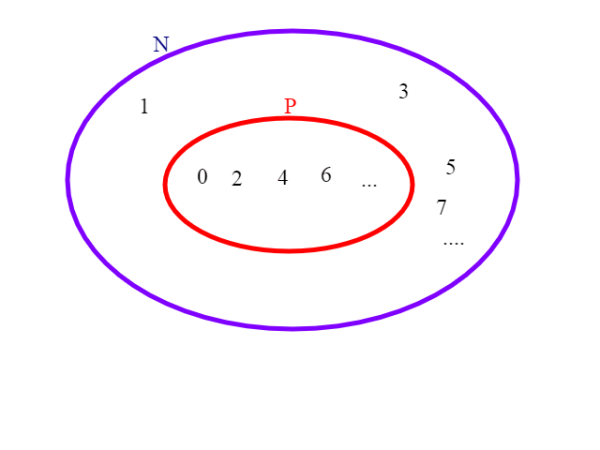
Galileo aveva notato questo fatto, usando però due insiemi diversi, l'insieme dei quadrati perfetti e l'insieme N dei naturali:

1	2	3	4	5	6	7	8
1	4	9	16	25	36	49	64

Anche i quadrati perfetti sono ugualmente numerosi a tutti i numeri naturali, basta associarli alle loro radici quadrate.

Nei prossimi articoli chiariremo meglio questo fatto assai strano, che è caratteristica degli insiemi infiniti.

 

Indice di tutti gli articoli di Umberto Cibien presenti in archivio-Matematica