LA SFERA DI POINCARÉ 6)Le varietà Riemmane .***
Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure
Riassunto della puntata precedente.
Nell'ultimo articolo abbiamo introdotto due concetti importanti; la base di uno spazio di vettori e il prodotto scalare. Mettiamoci in dove possiamo rappresentare un vettore tramite coordinate. La base non è altro che un insieme minimo di vettori che può generare con le sue combinazioni lineari tutto lo spazio vettoriale in questione. Abbiamo poi introdotto la metrica, e quello che viene "spaventosamente" chiamato tensore metrico. Non dimentichiamoci poi delle curve e della definizione di vettore velocità.
Superfici in
Ma torniamo alle nostre varietà differenziabili; in ogni punto alla varietà sappiamo che esiste un piano tangente, chiamiamolo . Il nostro obiettivo ora è trovare una base per
, che sarà legata alle equazioni parametriche che definiscono la superficie.
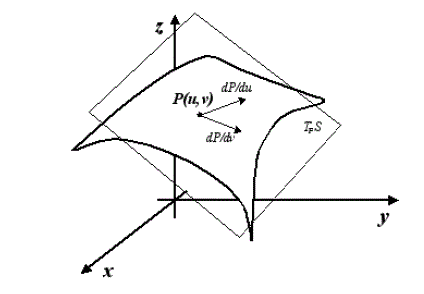
Esiste un sistema semplice per trovare una base per TpS; se nel piano u,v fissiamo una coordinata, diciamo u0 e facciamo variare l'altra (internamente chiaramente al nostro aperto dove è definita la superficie) otteniamo una retta parallela all'asse v (analogamente se fissiamo v0 e facciamo variare u otteniamo una retta parallela all'asse u). Ora, la retta u=u0 avrà come immagine una curva in , che sarà contenuta nella superficie S , essendo l'intervallo considerato contenuto in V.
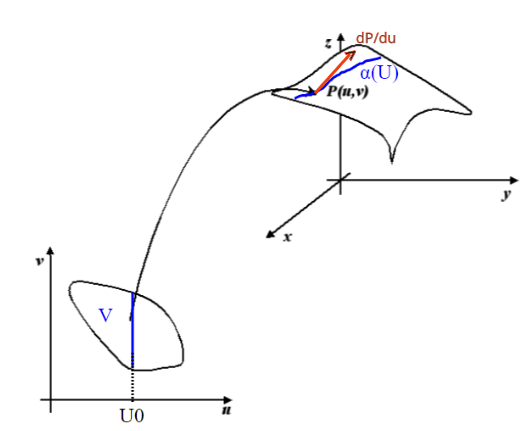
Le immagini dei punti della curva,che si possono ottenere tramite la funzione , dipendono da un solo parametro v e si possono quindi esprimere con
; (ricordiamo che parametri=1 vuol dire varietà di dimensione 1, ovvero una curva). Per trovare il vettore tangente alla curva, facciamo la derivata rispetto al parametro v; Essendo
, questa espressione costituisce una curva parametrica con parametro v; il vettore tangente alla curva lo troviamo subito derivando rispetto a v:
(nel disegno indichiamo sinteticamente tale vettore con dP/du).
Lo stesso dicasi per la linea coordinata u. Per semplificare le notazioni chiameremo questi due vettori semplicemente ; essi costituiscono una base* per TpS, che dipende dal punto di tangenza considerato.
(*: questo in teoria andrebbe giustificato più a fondo , ma per una volta credetemi sulla parola)
Continuiamo adesso con il nostro prodotto scalare, che sappiamo generare una metrica; restringiamo il prodotto scalare tridimensionale su a Tps e vediamo cosa salta fuori. Prendiamo due vettori p,q che stanno su TpS, che quindi saranno vettori ottenibili tramite combinazioni lineari dei vettori
; che costituiscono una base per il piano tangente.
( sono le coordinate dei vettori p,q)
Calcoliamo il prodotto scalare dei due vettori;
che si rifà ai prodotti scalari dei vettori della base; chiamiamo E,F,G tali prodotti:
che sono ovviamente dei numeri dipendenti dal punto P. Ritornando ancora al prodotto scalare, che è anche esprimibile in forma matriciale,analogamente a quanto visto nel precedente articolo, per fare il prodotto scalare in TpS di due vettori qualsiasi, o per calcolarne la norma (il modulo), possiamo usare i prodotti scalari E,F,G usati sulla base. Il prodotto scalare è quindi rappresentato dalla matrice:
detta anche tensore metrico, mentre E,F,G sono i coefficienti della metrica. Notiamo che
è il prodotto scalare dei due vettori della base. Sappiamo, nel caso euclideo (
), che F è nullo essendo i vettori della base ortogonali. Potendo essere F non nullo, si dice che F è la misura della non ortogonalità della base.
A differenza del caso euclideo, dove dato il piano la matrice M risulta costante , lo stesso non può dirsi per TpS, dove varia da punto a punto della superficie. Come prima applicazione,ci proponiamo, tramite il tensore M, di calcolare la distanza di due punti sulla superficie.
Versione “infinitesima” della metrica
Leggendo un articolo di geometria differenziale o di relatività, ci si imbatte una pagina si e una no in scritture del tipo:
oppure:
di solito questo, dopo pochi minuti, comporta per i non addetti ai lavori l'abbandono della lettura e la tendenza ad occuparsi di altro. Questo accade perché nessuno si prende mai la briga di dare una spiegazione anche solo sommaria di tale formalismo. Scritture di questo tipo sono poco intuitive, se non viste in un contesto tipo quello di questo articolo. Se vogliamo misurare una distanza che non sia quella fra due punti in o in
dove basta il teorema di Pitagora, ma sia lo spazio percorso per raggiungere due punti su una traiettoria curvilinea, per risolvere il problema ci troviamo davanti ad una versione infinitesima della distanza.
Dato un vettore w appartenente a TpS, consideriamo una curva passante per P e tangente a w
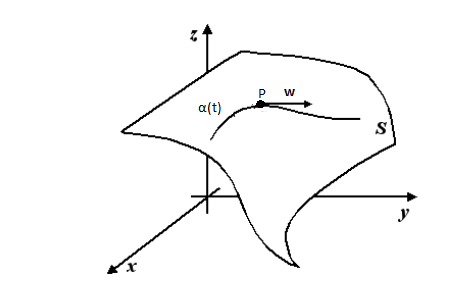
ricordando che :
otteniamo
se chiamiamo la lunghezza dell'arco infinitesimo,
, otteniamo:
1)
Questo elemento è detto anche elemento di linea. Ma veniamo al dunque; se vogliamo calcolare la distanza fra due punti A e B su una varietà differenziabile, dobbiamo tenere conto che non possiamo uscire da tale varietà, che è il nostro mondo. La distanza fra due punti "vicinissimi" la conosciamo, è quella definita dalla 1). Prendiamo quindi un percorso che unisca A e B e sommiamo tutti questi pezzettini infinitesimi (che corrisponde analiticamente a calcolare un integrale). Ma che percorso prendiamo? Quello che dà la minima lunghezza. Tale percorso prende anche il nome di geodetica. Ma non anticipiamo troppo i tempi..parleremo di questa definizione più volte nel seguito. Indichiamo comunque tale lunghezza in questo modo:
.
Che si legge: integrale dell'elemento ds lungo la curva .
L'importanza della metrica è enorme; la relatività generale ne fa ampio uso, e accenneremo come le equazioni di Einstein nel vuoto (che derivano dai principi relativistici) abbiano come incognita proprio la metrica. Una delle soluzioni (sotto particolari condizioni)è proprio quella di Schwarzschild, di cui si è ampiamente parlato in questo sito. In pratica, tutto parte da qui, per quanto riguarda la comprensione della forma dell'universo in cui viviamo.
Gli altri articoli di questa serie:





