Ormai stiamo spaziando da un argomento all'altro della matematica, anche  con piccoli concetti che, pur essendo intuitivi, forse non hanno mai avuto nella nostra esperienza matematica una precisa collocazione. Chiariamo bene prima il concetto di albero, per affrontare poi un simpatico paradosso che può essere denominato come la versione geometrica dell ultra famoso  paradosso di Russell.

Cominciamo col vedere cos'è un albero in matematica.

Chiaramente il concetto di albero in matematica, ha una profonda analogia con gli alberi genealogici, per cui tanto vale usare la stessa terminologia.

Un albero è un insieme di oggetti, chiamati nodi dell'albero, su cui è definita una relazione padre-figlio  che gode della seguente proprietà. Ogni nodo, tranne la radice, ha uno e un solo padre. La radice non ha padre.

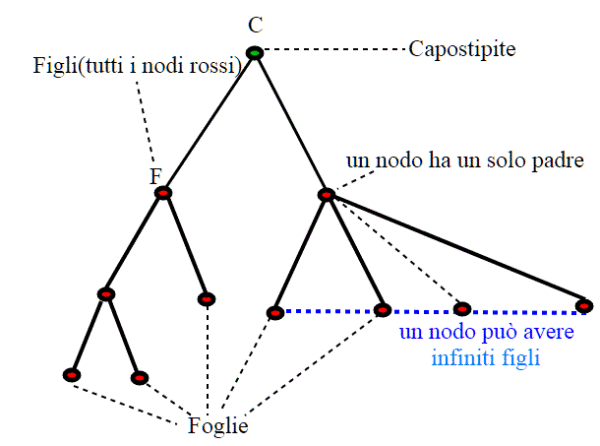
Ogni nodo ha zero o più figli. I nodi con zero figli si chiamano foglie dell'albero. E' ammessa la possibilità che un nodo abbia infiniti figli.

Parliamo  adesso dei discendenti.

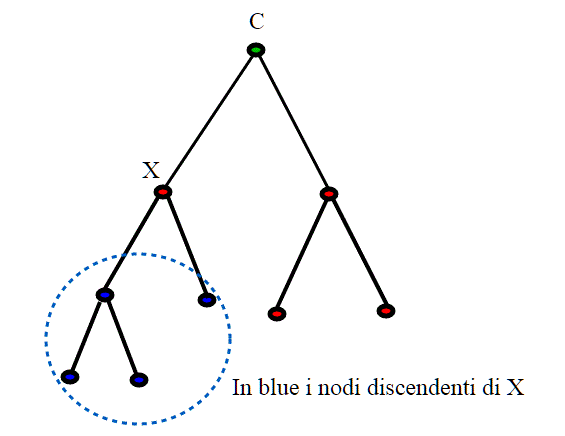
I discendenti di un nodo x sono quelli che si ottengono a partire da esso tramite un cammino finito, ovvero una successione finita di nodi che parte da X e in cui ogni nodo è figlio del precedente. Richiediamo, nella definizione di albero, che ogni nodo sia un discendente della radice (il capostipite).

Introduciamo ora un'altra definizione che riguarda gli alberi, quella di fondatezza:

Un albero è ben fondato se non ha cammini infiniti

Questo significa che prima o poi, qualsiasi sia il nodo padre, non ci sono più discendenti. E' come dire che una sorta di eredità di blocca. Notiamo la differenza fra cammino infinito e il fatto che un nodo possa avere infiniti figli. Questo può succedere anche se l'albero è ben fondato. L'importante è che i cammini, ovvero gli spostamenti da un nodo al figlio, non siano infiniti.

Una Osservazione sugli alberi ben fondati:

1. Se un albero contiene una copia di se stesso come sottoalbero, allora non è ben fondato.

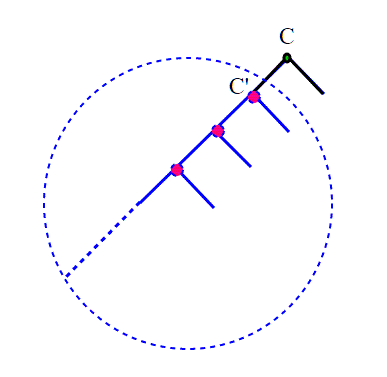
nella figura vediamo un albero con capostipite C che contiene un sottoalbero copia di se stesso con capostipite C'. Notiamo che , se accade questo, anche i sottoalberi dell'albero di partenza contengono una copia di se stessi.

Costruisco allora un cammino in questo modo: parto da C e mi sposto su C' che è la radice della sua copia; e da lì itero il procedimento, ovvero mi sposto sempre verso il sottoalbero che è copia di quello da cui sono partito, producendo in tal modo un cammino infinito.  Questo significa  che l'albero da cui sono partito, non è ben fondato.

Riflettiamo per ora su queste definizioni, con il secondo articolo vedremo come si articola il paradosso.