Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Abbiamo visto che un insieme numerabile contiene dei sottoinsiemi propri, che sono anch'essi numerabili. L'esempio era stato quello dei numeri pari e dei numeri dispari, che possono essere messi in corrispondenza biunivoca con l'intero insieme N. Consideriamo adesso un qualsiasi sottoinsieme proprio infinito X di N. Quale sarà sarà la sua cardinalità? Di sicuro X non potrà essere più numeroso di N, in quanto ha meno elementi (l'inclusione è propria). Vogliamo dimostrare che la sua cardinalità è ancora Aleph(0), che è la cardinalità di N. Prima di iniziare devo ricordare qualche nozione sugli insiemi e su i numeri naturali.

Insieme complementare.

Dato un insieme A e un suo sottoinsieme B, definiamo insieme complementare, l'insieme costituito dagli elementi di A che non appartengano anche a B.

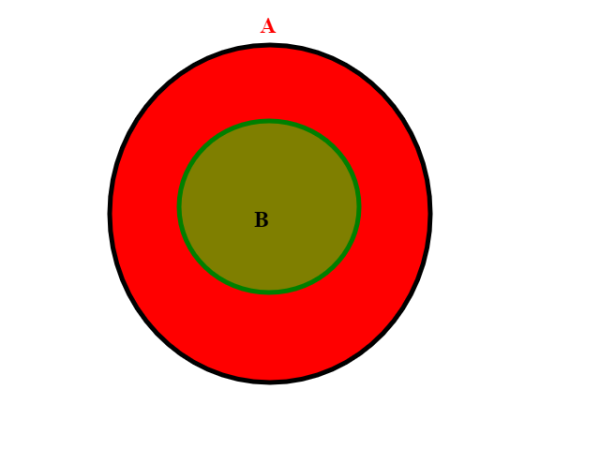
Nel caso evidenziato dalla figura, la parte rossa è l'insieme complementare di B in A. Indichiamo Con A-B il complementare di B in A. Notiamo che un elemento x o sta in A o sta nel complementare A-B.

Minimo di un insieme di numeri naturali

Tutti sappiamo come fare il confronto fra due numeri naturali distinti a e b per dire chi è il più grande; risulta o a < b oppure b>a. Definiamo minimo di un insieme X il numero naturale  più piccolo appartenente all' insieme, ovvero il numero m<=x per qualunque  x appartenente ad X. Ad esempio dato X={5,2,3,4,7} se indichiamo con min(X) il minimo di X;in questo caso è 2. Sembrerebbe così semplice stabilire il minimo di un insieme, ed è anche intuitivo farlo, nell'esempio vediamo subito che 2 è più piccolo di qualsiasi altro elemento di X. Ma nel caso X  non si possa elencare così esplicitamente, oppure sia infinito? In questo caso ci soccorre il:

Principio del buon ordinamento: Ogni insieme non vuoto di numeri naturali ha un elemento minimo. Questo principio fa parte della  base assiomatica data da Peano  per i numeri naturali, come il principio di induzione che abbiamo trattato nell'articolo precedente; il realtà basta uno dei due principi, perchè si dimostra che sono equivalenti.

Dato per vero  Il principio di induzione, che abbiamo visto nell'articolo precedente, possiamo dimostrare il principio del minimo ordinamento, che riscriviamo :

Per qualsiasi sottoinsieme non vuoto   , esiste un elemento minimo, cioè esiste m tale che ,  per ogni x appartenente ad X

Sia A un sottoinsieme dei naturali che non ha un elemento minimo: mostriamo che è vuoto dimostrando per induzione che il suo complementare N-A coincide con tutto l'insieme N dei naturali.

Base dell'induzione:

Lo 0 appartiene a N-A; se così non fosse dovrebbe appartenere ad A, e avremmo che A ha un elemento minimo (infatti 0 è il più piccolo numero naturale) contro l'ipotesi.

Passo induttivo:

supponiamo che N-A contenga i numeri naturali da o a n:

{0,...,n} ma allora N-A deve contenere anche n+1; altrimenti n+1 dovrebbe appartenere al suo complementare A; quindi A conterebbe n+1, ma non 0,..n che sono tutti minori di esso, quindi A avrebbe come minimo n+1, contro l'ipotesi. Quindi {0,...,n,n+1}. ma allora, per il principio di induzione {0,...,n} è vera qualsiasi sia il numero naturale n.

Dunque N-A coincide con N e quindi A è vuoto.

Funzioni crescenti.

Consideriamo una funzione f: N-->N; diremo che tale funzione è crescente se n<m implica  f(n)<f(m). Notiamo che una funzione crescente è iniettiva; infatti se supponiamo che n<>m allora f(n)<>f(m) (se n,m sono diversi, uno dei due è maggiore dell'altro, quindi questo vale anche per le immagini,che quindi sono diverse).

Sottoinsiemi infiniti di N

Fra i sottoinsiemi infiniti di N, c'è nè uno molto noto: l'insieme X dei numeri primi,  X={2,3,5,7,11,13,17,...}. Vogliamo dimostrare  che questo insieme (come del resto ogni sottoinsieme infinito di N) può essere messo in corrispondenza biunivoca con N. Prendiamo X come esempio, ma vogliamo arrivare ad una dimostrazione generica. Come possiamo creare questa corrispondenza? L'idea è quella di enumerare gli elementi di X in ordine crescente:

N	0	1	2	3	4	5	6
X	2	3	5	7	11	13	17

Senza rendercene conto abbiamo costruito una corrispondenza biunivoca fra N e l'insieme X, che associa a 0-->2,1-->3, 2-->5, 3-->7, 4-->11 ecc. qualsiasi sia n, possiamo sempre trovare l'n-esimo numero primo, visto che i numeri primi sono infiniti.Ma nel caso generico, come possiamo fare questa operazione? Dobbiamo ordinare l'insieme X in modo crescente ma dobbiamo dare una funzione,  una regola, un algoritmo che ci permetta di trovare per ogni numero naturale n il corrispondente nell'insieme X. Nell'articolo precedente, abbiamo definito le funzioni definite per ricorrenza, o ricorsive. L'idea è quella di trovare dapprima il primo elemento dell'insieme X, poi di togliere tale elemento dall'insieme e trovare quindi il secondo elemento e così via. Dato un sottoinsieme proprio infinito   X di N, definiamo la seguente funzione ricorsiva (F: N--->X) in tal  modo:

F(0)=min X

F(n+1)=min X-{F(1),F(2),F(3),...F(n)}

(togliamo ogni volta ad X  tutti i valori calcolati precedentemente, poi facciamo il minimo. Per quanto visto sopra sul principio del minimo ordinamento tale minimo esiste sempre, in quanto l'insieme X è infinito, quindi  X-{F(1),F(2),F(3),...F(n)} non è mai vuoto.

Questa definizione può spaventare! In realtà se la illustriamo con un esempio diventa molto più comprensibile. Prendiamo come X il sottoinsieme infinito di N dei numeri primi: X={2,3,5,7,11,13,17,..}

F(0)=min X=2

F(1)=min {2,3,5,7,11,13,17,..}-{F(0)}=

min {3,5,7,11,13,17,..}-{2}=min {3,5,7,11,13,17,..}=3

F(2)=min {5,7,11,13,17,..}-{F(0),F(2)}=

min {2,3,5,7,11,13,17,..}-{2,3}=min {5,7,11,13,17,..}=5

Visto in altro modo, in forma tabellare, possiamo costruire la sequenza:

n	F( 0)	F(1)	F(2)	F(3)	F(4)
0	2	3	5	7	11
1		3	5	7	11
2			5	7	11
3				7	11
4					11

Osserviamo che otteniamo proprio quello che volevamo, ossia dei valori crescenti per F(n) cioè F(n+1)>F(n) ;questa è una conseguenza di come è costruita, come si vede dall'esempio (più precisamente: parto da zero e trovo il minimo di X, al passo successivo prima tolgo il minimo a X, poi calcolo il nuovo minimo, che senz'altro è più grande del passo precedente, poi tolgo a X i due valori trovati e ricalcolo il minimo, ottengo ancora un valore più grande..e così via) .

F è una funzione biunivoca di N in X; quindi X è numerabile.

(Ho messo la dimostrazione alla fine dell'articolo per non appesantire troppo l'esposizione; è abbastanza tecnica. Comunque non è necessaria per comprendere i concetti che seguono.)

Ogni sottoinsieme infinito di un insieme numerabile è numerabile

Per N lo abbiamo dimostrato; Prendiamo adesso come M un qualsiasi insieme numerabile, e sia Y un suo sottoinsieme proprio infinito. Se M è numerabile, esiste una funzione F: M---> N biunivoca.

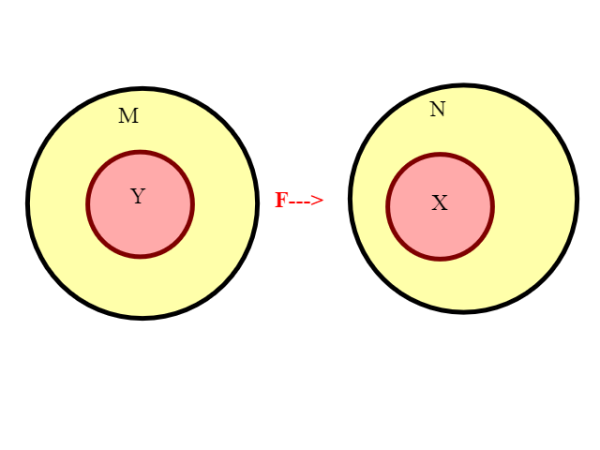
Tale funzione manda il sottoinsieme Y di M in X=F(Y), e la funzione F ristretta ad Y è una applicazione biunivoca di Y--->X=F(Y), sottoinsieme di N; ma sappiamo che X è numerabile (è un sottoinsieme infinito di N), quindi anche Y lo è.

(Ricordo  che  F: Y-->F(Y)=X è una funzione suriettiva, infatti copro tutto F(Y) per la definizione stessa di immagine)

Confrontare la cardinalità di due insiemi.

Fino ad ora siamo riusciti a dire che due insiemi (infiniti) hanno la stessa cardinalità se esiste un corrispondenza biunivoca fra di essi. Ma se ciò non si verifica?  Vogliamo cioè definire quando la cardinalità di un insieme X sia minore di quella di un insieme Y.  Diremo che |X|<=|Y| se esiste una funzione iniettiva f di X in Y: f: X--->Y (e sottolineiamo che una funzione iniettiva di X in Y è una corrispondenza biunivoca di X in un sottoinsieme di Y, che non è altro che l'immagine di X, f(X)). Diremo invece che |X|<|Y| se esiste una applicazione iniettiva f di X in Y, ma tale applicazione non è suriettiva. In parole povere non copre tutti gli elementi di Y.

Il minimo ordine di infinito:Aleph(0)

Esistono ordini di infinito minori di quello dei naturali? Sia X un insieme infinito con cardinalità |X|<=|N|. Per quanto visto sopra sul confronto fra numeri cardinali, esiste una funzione iniettiva

f:X-->N ; chiamiamo Y l'immagine di X ,Y=f(X). Ma allora la funzione f-->Y=f(X) è anche suriettiva, quindi è biunivoca. Ma allora |X|=|Y|. Ma Y è un sottoinsieme infinito di N, quindi è numerabile. Ma allora |X|=|Y|=|N|. Dunque X è numerabile, quindi Aleph(0) è il minimo numero cardinale.

Appendice

La funzione ricorsiva:

F(0)=min X

F(n+1)=min X-{F(1),F(2),F(3),...F(n)}  dove X è un sottoinsieme infinito di N

è una  funzione biunivoca di N---> X

Abbiamo visto che  F è crescente, ma  allora è iniettiva, per quanto visto prima sulle funzioni crescenti.

Notiamo poi  che F(n)>=n ; questo fatto si può dimostrare per induzione.

Infatti è vera per 0; F(0)=min X >=0 . Supponiamo sia vera per n, dimostriamola per n+1.

F(n+1)>F(n); per ipotesi induttiva, F(n)>=n, allora F(n+1)>F(n)>=n, quindi F(n+1)>n, ma questo vuol dire F(n+1)>=n +1. Quindi F(n)>=n qualsiasi sia n.

Sfruttiamo questo fatto per dimostrare che F è anche suriettiva. Dato un qualsiasi x appartenente ad X,  vogliamo dimostrare che x appartiene all ' immagine di F({0,1,...,x}).  Ma F({0,1,...,x})={F(0),F(1),.. F(x)}

(in pratica se prendiamo un insieme abbastanza grande, la sua immagine andrà a contenere x)

ma F è crescente! Quindi l'immagine di F({0,1,...,x}) è costituita dagli m appartenenti ad X, tali che m<=F(x). Ma sappiamo che x<=F(x), quindi x appartiene all'immagine   F({0,1,...,x}).

Articoli precedenti:

Cantor pare quinta,Il principio di induzione

Cantor, parte quarta. L'abergo di Cantor

CANTOR parte Terza, gli insiemi numerabili

CANTOR parte Seconda: Corrispondenze e funzioni

CANTOR parte prima, gli insiemi

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica