Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Dopo una lunga pausa ho pensato di riprendere gli articoli sugli insiemi infiniti e sulle loro applicazioni a cose decisamente "strane". In questo articolo abbiamo visto la necessità di inserire nella teoria degli insiemi un assioma, detto " assioma della scelta" che ci permette di effettuare infinite scelte su famiglie di insiemi. L'assioma della scelta è proprio un assioma, pur avendo una giustificazione intuitiva; cè chi lo prende per buono e chi no. Accettare l'assioma della scelta porta a situazioni paradossali, come l'insieme di Vitali e il paradosso di Banach, che spero di riuscire a sviscerare.Rinunciare a tale assioma comporta invece la perdita  di importanti risultati sugli insiemi infiniti, quali ad esempio l'unione numerabile di insiemi numerabili, il teorema di Zermelo o l'equivalente lemma di Zorn.

Anticipiamo una nozione che ci servirà più volte nell'articolo:

Equidecomponibilità

Parliamo di insiemi.Indichiamo  con questo simbolo  l'unione disgiunta di C,D: .

E' semplicemente l'unione di due insiemi disgiunti, ossia tali che  . Diciamo che due sottoinsiemi A, B sono equidecomponibili se è possibile trovare degli insiemi (disgiunti) A1,..An e dei movimenti rigidi   tali che

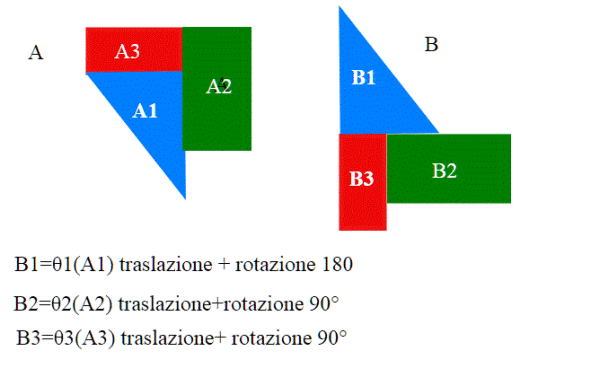
Come al solito è più difficile dirlo che farlo: Vediamolo nel piano:nella figura A e B sono degli insiemi apparentemente molto diversi , ma sono equidecomponibili

 

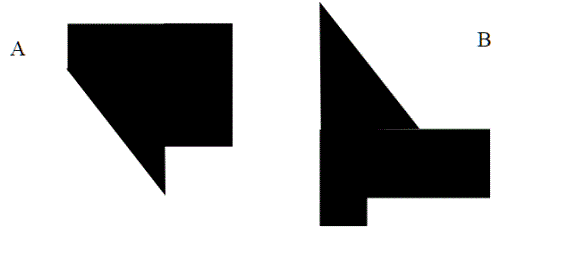
Misurare gli insiemi

Ci proponiamo di definire cos'è la misura di un insieme.  Chiamiamo  tale misura,che agisce sui sottoinsiemi di  .Avremo quindi  una applicazione definita su sottoinsiemi di  a valori in , ovvero sui numeri reali positivi o nulli . La misura  è dunque una funzione  .

Misurare un segmento è facile, così pure altre semplici figure geometriche nel piano, o i solidi principali nello spazio; In ogni caso otteniamo tramite formule più o meno complesse una lunghezza, una superficie o un volume.

La stessa cosa non si può dire per un insieme qualsiasi di punti, che siano essi in . Non ci preoccupiamo però di come calcolare una tale misura, ossia quali tecniche usare. Ma quali proprietà deve avere una tale misura? Bè, ci farebbe comodo scomporre l'insieme che misuriamo in parti  e poi sommare le misure delle varie parti.  Per applicare tale proprietà, abbiamo proprio introdotto la nozione intuitiva di equidecomponibilità; possiamo pensare di scomporre un insieme A in tanti pezzi A1..An che siano  disgiunti. Cosa  ci aspettiamo da questa misura ?  Che la somma delle misure dei singoli pezzi A1..An sia uguale alla misura dell'unione dei pezzi, e di conseguenza alla misura di A. Scomponiamo A nell' unione di tanti pezzi disgiunti:In modo formale:

; questa scrittura significa che facciamo variare k nell insieme N, che è l'insieme dei numeri naturali. Si parla di unione numerabile. La nostra misura deve avere perciò una "numerabile additività":

Chiaramente il fatto che valga l'additività nel caso di unione numerabile, implica che valga anche quando parliamo di unioni finite. Basta considerare infatti gli Ai tutti vuoti da un certo punto in poi.

Cos'altro deve avere la nostra misura per definirsi valida per i nostri scopi?

Se misuriamo un segmento, la sua misura deve chiaramente coincidere con la misura elementare. Qual'è la misura elementare di[0.1]? E'chiaramente 1. Quindi  >0.

In questo articolo avevamo accennato al gruppo delle isometrie piane, ossia ai movimenti rigidi. Vogliamo anche che la nostra  misura sia invariante per movimenti rigidi.

Detto in parole povere: se prendiamo un insieme e lo facciamo ruotare o traslare e lo misuriamo prima e dopo dobbiamo avere lo stesso risultato. In modo formale, indicando con  una isometria di :

.

Le proprietà che vogliamo dalla nostra misura, ovvero che ci farebbero comodo,sono quindi queste.

Sono cose abbastanza intuitive; non è invece intuitivo che se ci mettiamo in R e vogliamo trovare una tale misura, ci accorgiamo che non esiste. Ed è qui che interviene Vitali con il suo insieme: tale insieme non è misurabile. In genere la dimostrazione di questo fatto viene tralasciata perchè ritenuta complessa. ma con quello che abbiamo fatto sugli infiniti di  Cantor, possiamo provarci .

L'insieme di Vitali.

Mettiamoci sulla retta, che è pur sempre un caso di spazio , con n=1

Consideriamo l'intervallo [0,1]: in esso definiamo la relazione d'equivalenza:

  se e solo se

detto in parole povere, consideriamo  nell'intervallo [0,1] coppie tali che la loro differenza sia razionale.

Riuscire a visualizzare quali siano le classi che origina tale definizione è impresa ardua; sta di fatto che però è una relazione di equivalenza. Infatti:

i) è riflessiva in quanto x-x=0 è un numero razionale

ii) è simmetrica: se x-y=q, y-x=-q

iii) è  transitiva: (x-z)=(x-y)-(y-x); essendo le due differenze a secondo membro  razionali, anche il primo membro è razionale.

Notiamo che se prendiamo una classe qualsiasi, essa è un insieme numerabile.

Una classe ,per esempio, è costituita da numeri razionali in [0,1]. Infatti presi qualsiasi due numeri razionali in [0,1],la loro differenza è ancora un numero razionale. Chiaramente l'insieme dei razionali in[0,1] è un insieme numerabile. Preso un qualsiasi numero irrazionale in [0,1], ad esempio , per avere tutti gli elementi della sua classe,basta sommargli un razionale q, ovvero i numeri equivalenti sono del tipo  , con l'avvertenza di prendere i razionali per cui ; anche qui abbiamo una infinità numerabile di razionali che soddisfano a tale richiesta. Per chi non ne fosse convinto, prendiamo un q positivo e tale  cioè =0,292...

quindi basta prendere un 0<q<0.29=29/100; tutti i q=29/n con n>100 vanno bene, e sono quindi una infinità numerabile.

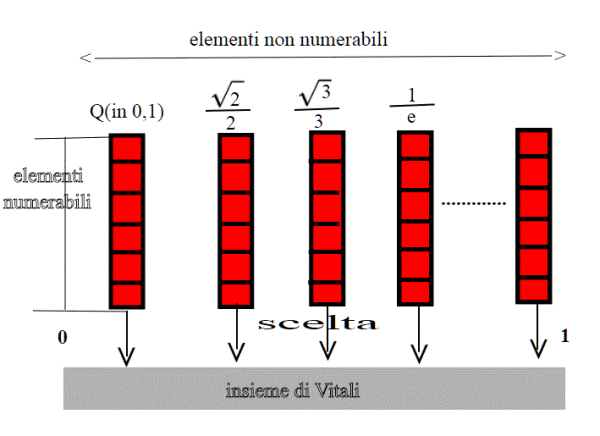
Per quello che abbiamo visto sulle classi di equivalenza, esse formano una partizione dell'intervallo [0,1]. Poichè ogni classe di equivalenza è un insieme numerabile, la famiglia delle classi di equivalenza ha la potenza del continuo. Infatti se consideriamo l'insieme di tutte le classi di equivalenza indotte dalla relazione appena definita,queste devono essere una infinità non numerabile, poiché se fossero un'infinità numerabile avremmo che l'insieme [0,1] stesso sarebbe numerabile (in quanto unione numerabile di insiemi numerabili). Questo fatto (unione numerabile di insiemi numerabili) lo avevamo visto qui.

Supponiamo adesso di  scegliere un rappresentante per ogni classe di equivalenza.  Chiamiamo V tale insieme; che questa scelta si possa fare è garantito dall 'assioma della scelta. Quindi V altro non è che l'insieme quoziente  della relazione .

Dato adesso un razionale x, definiamo traslato dell'insieme V, e lo indichiamo con  V+x, l'insieme :

V+x={x+y con y appartenente a V}.

Consideriamo adesso due numeri razionali q1,q2; vogliamo dimostrare che se q1<>q2 allora  i due insiemi traslati di V. q1+V, q2+V sono insiemi disgiunti, ovvero non hanno elementi in comune.

Supponiamo per assurdo che x  appartenga all'intersezione Vogliamo dimostrare che q1=q2;

sappiamo che x=q1+y1 con y1 appartenente a V; allo stesso modo, x=q2+y2, con y1 appartenente a V.

quindi:

x=q1+y1

x=q2+y2

sottraendo membro a membro otteniamo:

0=q1-q2+y1-y2;

y1-y2=q2-q1; ma q2-q1 è un numero razionale, quindi y1,y2 stanno nella stessa classe d'equivalenza

Ma V ha un solo elemento per ogni classe di equivalenza, quindi y1=y2. Di conseguenza q1=q2.

Trovandoci sulla retta quali isometrie sono possibili? Bè le traslazioni. Perchè abbiamo introdotto gli insiemi traslati? Perchè vogliamo sfruttare l'invarianza della misura rispetto alle traslazioni.

Vogliamo adesso dimostrare il seguente fatto:

i traslati razionali di V, r+V, con r razionale appartenente a [-1,1] coprono con la loro unione l'intervallo [0,1] ed inoltre  la loro unione è contenuta in [-1,2]

dobbiamo per prima cosa dimostrare che:

prendiamo un x appartenente a [0,1] ; c'è un unico y appartenente a  tale che r=x-y. Poichè x, y sono in [0,1]  , , quindi  x=r+y, con r razionale,   e quindi x appartiene ad un insieme del tipo r+V. il fatto poi che  è banale; infatti il valore più piccolo di r è-1,quello di un elemento di V è zero, quindi -1+o=-1; analogamente 1+1=2

L'insieme di Vitali non è misurabile

Supponiamo che V sia misurabile.

Partiamo da lontano; nella definizione di misura,abbiamo detto che deve essere invariante per traslazione; se prendiamo il nostro insieme V anche il suo traslato r+V deve essere misurabile e inoltre 

forse non lo abbiamo detto esplicitamente, ma se  è una misura, e  allora .Infatti se , possiamo scomporre B in una unione disgiunta: 

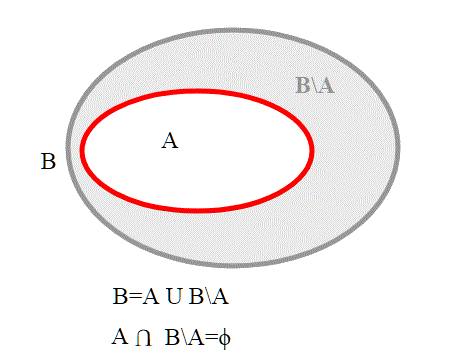
se applichiamo l'additività della misura,,

quindi 

quindi essendo ,

abbiamo poi parlato di unione numerabile; se Abbiamo una famiglia Ai numerabile  di insiemi misurabili,  si deve avere:

;

consideriamo adesso il nostro insieme  (lo abbiamo costruito così apposta!)

nel nostro caso gli Ai sono costituiti dagli r + V; non dimentichiamo infatti che i razionali compresi fra-1 e 1 sono un insieme numerabile. Applichiamo l'additività numerabile a questi insiemi, che come abbiamo dimostrato sopra sono disgiunti, e teniamo conto anche dell'invarianza per traslazione

()

 

l'ultimo membro dell'eguaglianza è una somma infinita di un termine costante; Se V è misurabile possiamo avere due casi:

 

:

 

Abbiamo poi visto che:

; ma zero o infinito non sono compresi fra 1 e 3. Dobbiamo quindi concludere che V non è misurabile, perchè supporlo tale porta ad un assurdo.