Cantor, parte 15°: L'assioma della scelta .
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Insiemi ben ordinati.
Abbiamo già visto degli esempi di insiemi ben ordinati: i numeri naturali .L'insieme dei numeri naturali è totalmente ordinato (un insieme è totalmente ordinato se presi comunque due elementi, posso sempre decidere se uno è maggiore dell'altro).Genericamente, quando si parla di insiemi ordinati, non si è sicuri che questi insiemi siano totalmente ordinati, per cui in generale si dice che tali insiemi sono parzialmente ordinati. Un esempio di insieme parzialmente ordinato è l'insieme delle parti di un insieme X, prendendo come ordine l'inclusione. Se due sottoinsiemi di X non sono uno contenuto nell'altro, non sono confrontabili.

Se oltre ad essere totalmente ordinati, tali insiemi soddisfano al principio del minimo (ovvero ogni sottoinsieme di X ha minimo), allora si dicono ben ordinati. Perchè riprendiamo questi concetti? Per rispondere a questa domanda: é sempre possibile confrontare la cardinalità di due insiemi? Cantor pensava di si ,a patto che ogni insieme si possa ben ordinare, anche se il nesso non è così immediato (vedremo che in due insiemi ben ordinati si può sempre definire una applicazione iniettiva di uno nell'altro).
Nel 1904 Ernst Zermelo ha dato una dimostrazione rigorosa del fatto che ogni insieme si può bene ordinare. Tale dimostrazione dipende sostanzialmente dall'accettazione dell'assioma della scelta,prima però dovremmo introdurre dei nuovi concetti sugli insiemi parzialmente ordinati, e considerare il fatto che l'assioma della scelta implica il lemma detto di Zorn. Lo schema che seguiremo in questa serie di articoli, sarà questo:
Assioma della scelta Lemma di Zorn
insiemi ben ordinati
confronto fra cardinali. Non ci resta che partire dall'assioma della scelta.
L'Assioma della scelta
Come già detto, Zermelo si occupo' di sistemare la teoria degli insiemi dal punto di vista assiomatico. Questo perchè la trattazione iniziale di Cantor(strettamente intuitiva) e detta anche "teoria ingenua degli insiemi", poteva dar adito a una serie di paradossi (quello più famoso quello di B.Russel). Nacque perciò la necessità della costruzione di una base assiomatica in modo rigoroso. Non tratteremo tutti gli assiomi di Zermelo , ma solo il più importante, che permette di risolvere (tramite una sua enunciazione equivalente, il lemma di Zorn) il problema di ben ordinare qualsiasi insieme. Il lemma di Zorn ci servirà anche per trovare la cardinalità dell'insieme prodotto in caso di insiemi infiniti qualsiasi (noi lo abbiamo visto solo nel caso degli insiemi numerabili, ma dobbiamo ancora dimostrarlo per il piano euclideo, ovvero R x R).
L'assioma della scelta stabilisce che:
Data una famiglia non vuota di insiemi non vuoti esiste una funzione che ad ogni insieme della famiglia fa corrispondere un suo elemento.
Informalmente, quando ci viene data una collezione di insiemi non vuoti possiamo costruire un nuovo insieme "scegliendo" un singolo elemento da ciascuno di quelli di partenza. Praticamene come posso procedere? Devo scegliere un elemento da uno degli insiemi, un altro elemento da un altro degli insiemi, e così via.
E’ evidente che se gli insiemi sono infiniti, le scelte devono essere fatte una ad una, e non si termina mai; ma è altrettanto evidente che una scelta di un elemento da ogni insieme è sempre possibile.
Un tipico esempio (dovuto a B. Russell:) con cui si spiega il senso dell'assioma è il seguente:
"Per scegliere un calzino da ognuna di infinite paia di calzini serve l'assioma della scelta,mentre l'assioma non e necessario se si vuole scegliere una scarpa da ognuna di infinite paia di scarpe."
supponiamo cioè di avere un numero infinito di paia di scarpe e di voler definire un insieme che contiene una (e una sola) scarpa di ogni paio; possiamo farlo senza problemi considerando ad esempio l'insieme delle scarpe destre. I problemi nascono se abbiamo un numero infinito di paia di calzini (supponendo che il destro e il sinistro non siano distinguibili), e vogliamo considerare come prima un insieme che contenga un calzino per ognuno di essi: non possiamo più parlare dell'insieme dei "calzini destri" e non abbiamo in effetti nessun modo di distinguere i due elementi di un paio, cioè di avere una funzione di scelta che ci assicuri di poterne scegliere contemporaneamente uno da ogni insieme. Per poter dire che un tale insieme comunque esiste dobbiamo invocare l'assioma della scelta.
Enunciato formale dell'assioma.
Definiamo prima cosa intendiamo per famiglia indiciata di insiemi; semplicemente una collezione di insiemi che abbiamo in qualche modo contrassegnato con un indice i; abbiamo già trattato collezioni di questo tipo (gli intervalli incapsulati,con n numero naturale). Qui in generale l'indice non è un numero naturale, ma appartiene ad un certo insieme I.
Di seguito useremo il simbolo per indicare l'appartenenza di un elemento ad un insieme, e i " : (due punti) per dire "tale che".
Passiamo allora all'enunciato dell'assioma:
Data una famiglia di insiemi non vuoti
, esiste una funzione f con dominio F, che manda ogni
in

L'importanza dell'assioma della scelta sta nel garantire l'esistenza di funzioni che potrebbero non essere definibili tramite una regola esplicita.
Cerchiamo di chiarire l'assioma con un esempio; supponiamo di considerare dei sottoinsiemi di R,
; per l'assioma della scelta, esiste una funzione che ad ogni
associa un elemento appartenente ad
, ma non sappiamo esprimere tale funzione esplicitamente; nel caso gli
siano sottoinsiemi di N invece che di R, riusciamo ad esplicitare una funzione di scelta in questo modo: f(
)=min
,minimo che sappiamo esistere qualsiasi sia il sottoinsieme
. Notiamo che non possiamo applicare la stessa definizione di f al caso di sottoinsiemi Ai di R, in quanto un sottoinsieme di R (anche se limitato) non sempre ha minimo (si pensi ad un intervallo aperto).
L'esempio si limita a sottoinsiemi di numeri naturali; In realtà e valido per qualsiasi insieme ben ordinato: se ogni insieme si può ben ordinare (teorema di Zermelo), allora vale l'assioma della scelta:
Consideriamo una famiglia di insiemi non vuoti
, e l'insieme
Se per ipotesi l'insieme
è ben ordinato, vuol dire che ogni sottoinsieme Ai ha minimo. Consideriamo la funzione f con dominio F, che manda ogni
nel minimo di Ai,
. Questa è una funzione di scelta per la famiglia Ai.
(abbiamo così anticipato che il Teorema di Zermelo, la cui dimostrazione verrà data nei prossimi articoli, implica l'assioma della scelta).
Vediamo subito delle conseguenze dell'assioma della scelta.
Se esiste un funzione f suriettiva f: B-->A, allora esiste una funzione iniettiva g di g: A-->B
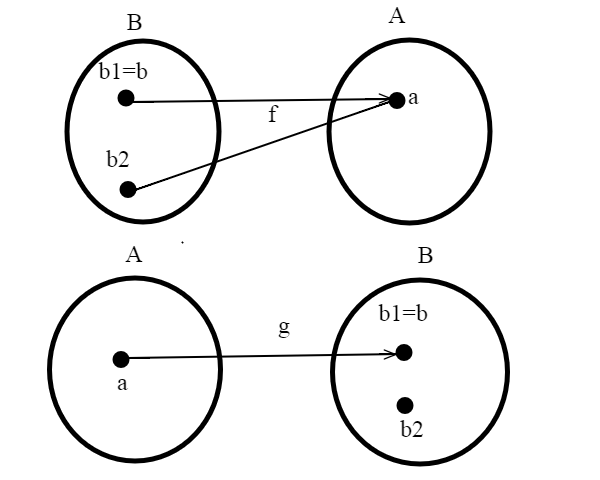
dobbiamo definire una funzione g: di A --->B; preso un qualunque a appartenente ad A, sappiamo, essendo f suriettiva, che esistono uno o più appartenenti a B, tali che
; grazie all'assioma ne scegliamo uno e lo chiamiamo b ; definiamo g(a)=b e abbiamo una funzione iniettiva(la funzione g è iniettiva perchè f è una funzione).
NB: questo ci dice che per dimostrare che |A|<=|B,ovvero che la cardinalità di A è minore di quella di B, basta trovare una funzione suriettiva di |B | in |A|.
Approfitto aprendo una piccola parentesi, per applicare subito questo importante risultato (derivante dall'assioma della scelta) agli insiemi numerabili.Abbiamo visto che l'unione di due insiemi numerabili è numerabile. Usando il principio di induzione, si può dimostrare che l'unione finita di insiemi numerabili è numerabile( per n=2 è vera, supposta vera per n ,
è allora numerabile, basta allora scrivere
e ho ancora l'unione di due insiemi numerabili) ; e se abbiamo una unione numerabile (quindi infinita) di insiemi numerabili?
L'unione di una famiglia numerabile di insiemi numerabili è numerabile.
Essendo ogni An numerabile, esiste una corrispondenza biunivoca gn: N-->An per ogni n: . Consideriamo adesso l'insieme N x N e costruiamo un funzione
ponendo
; f è suriettiva.Infatti se
, allora
per qualche n; quindi (essendo
suriettiva) esiste m tale che
Essendo f suriettiva,per quanto visto sopra, esiste una funzione iniettiva , quindi
essendo N x N numerabile; ma allora
è numerabile, essendo
il minimo ordine di infinito.
Nel prossimo articolo, vedremo come l'assioma della scelta implichi qualcosa di molto importante, il lemma di Zorn. Prima di arrivare alla formulazione del lemma, dovremo però acquisire delle importanti nozioni sugli insiemi ben ordinati. Il lemma continua a sembrare qualcosa di misterioso,anche un po' per il nome; ma non è altro che una formulazione equivalente all'assioma della scelta, però di più facile applicazione in certe dimostrazioni.






1 commento
Gli assiomi sono necessari nella matematica; ne abbiamo le prove dal tempo di Euclide. Ci sono dei concetti primitivi, che non è possibile scomporre ulteriormente.
Capire il perché della necessità di formulare l'assioma ella scelta (uno dei più importanti assiomi della matematica moderna) è un'impresa ardua. Spero di aver dato le indicazioni per una comprensione più raffinata.