Matematiche pure 3)I gruppi della matematica moderna **/***

Categorie: Matematica Tags: matematiche superiori Scritto da: Umberto Cibien Commenti:1

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

Continuiamo il nostro percorso sui prerequisiti fondamentali delle matematiche pure. Dopo esserci occupati di relazioni di equivalenza, fondamentali in ogni settore delle matematiche astratte, e di funzioni biunivoche (definizione di numero cardinale) ci occuperemo di una struttura molto nota e molto usata nella matematica moderna, quella di gruppo.

Un po' di storia

Lo studio dei gruppi è cominciato in Francia all’inizio dell’800, in relazione alla ricerca di formule risolutive per le equazioni algebriche, e ha riguardato inizialmente i gruppi finiti di permutazioni,iniziati da Évariste Galois negli anni 1830. In seguito a contributi provenienti da altri settori della matematica come la teoria dei numeri e la geometria, la nozione di gruppo fu generalizzata e definita stabilmente attorno al 1870.

Prima di dare la definizione di gruppo, alcuni concetti preliminari.

Operazione binaria interna

Dato un insieme A, una operazione binaria interna altro non è che una corrispondenza che ha come dominio l'insieme prodotto di A, e come codominio A; se indichiamo con * tale corrispondenza: $\bg_white *:A\times A\rightarrow A$ , essa associa alla coppia (a,b) il risultato di una certa operazione che indichiamo con a*b

(in pratica a*b=*(a,b). E' importante notare che il risultato dell'operazione resta all'interno dell'insieme; questa è la proprietà basilare di ciò che stiamo definendo, il fatto appunto che gli elementi di un insieme formano proprio un "gruppo".

Se ad esempio consideriamo l'operazione"-" ovvero la sottrazione (a-b), essa è una operazione binaria interna se come insieme A prendiamo Z (interi); Ma se come insieme prediamo quello dei numeri naturali N questo non è vero (se a<b, a-b<0 che non è un numero naturale.

Proprietà dell'operazione binaria interna

Proprietà associativa

Se a,b,c sono elementi di A, allora (a*b)*c=a*(b*c)

Cosa vuole dire? Vuol dire che è indifferente se abbiamo tre elementi a,b,c , eseguire prima l'operazione fra a e b e tale risultato comporlo con c, oppure comporre a con il risultato dell'operazione con b e c.

Lo abbiamo visto con i numeri e le usuali operazioni fin dalle scuole elementari; se devo fare 1+5+2 è indifferente fare 1+5=6, e poi 6+2=8, oppure 5+2=7, 1+7=8. Questo non è sempre vero; basti pensare alla sottrazione definita nei numeri relativi. In essa ad esempio fare (1-5)-2 che dà -6 non è la stessa cosa che fare 1-(-5-2) che dà 8.

Elemento neutro

Esistenza di un elemento e appartenente ad A, tale che e*a=a*e=a qualsiasi sia a appartenente ad A.Pensando ai numeri, se l'operazione è la somma, l'elemento neutro è lo zero (a+0=a), se invece consideriamo la moltiplicazione e=1 (a*1=a).

Inverso

Esistenza di un elemento $\bg_white a^{-1}$ detto inverso, che sia tale che $\bg_white a^{-1}*a=a*a^{-1}=e$ , qualsiasi sia a. Sempre nel caso numerico, se l'operazione è la somma e siamo nell'insieme Z l'inverso di a è -a (a+-a=0); se l'operazione è il prodotto e siamo nell'insieme Q dei razionali, l'inverso di a è proprio quello che chiamiamo inverso, ovvero $\bg_white a^{-1}=\frac{1}{a}$ , infatti il prodotto dà 1 (dobbiamo però limitarci ai numeri $\bg_white a \neq 0$ per avere un gruppo, ossia considerare Q\{0}).

Commutatività

L'operazione * è detta commutativa, se qualsiasi siano a,b appartenenti ad a, a*b=b*a. La somma e il prodotto di numeri interi sono operazioni commutative; la sottrazione no.

Definizione di gruppo

Dato un insieme A in cui sia definita una operazione binaria interna *, diciamo che la coppia (A,*) è un gruppo se l'operazione * soddisfa le seguenti condizioni:

* è associativa
per * esiste l'elemento neutro
per ogni A esiste l'inverso

se inoltre vale anche la proprietà commutativa, il gruppo si dice abeliano (o commutativo).

L'ordine di un gruppo A (identifichiamo il gruppo con l'insieme in cui è definita l'operazione *) non è altro che la cardinalità dell'insieme A; nel caso A sia finito è il numero di elementi di A, altrimenti è la cardinalità che abbiamo visto negli infiniti di Cantor . La cardinalità di A si indica sempre con |A|.

Un piccolo esercizio: in un gruppo l'inverso di un elemento è unico.

Supponiamo per assurdo di avere due inversi per a;indichiamo con a',a'' i due inversi di a .

allora $\bg_white a''=a''\cdot e=a''\cdot (a\cdot a')=(a''\cdot a)\cdot a'=e\cdot a'=a'$ dove la terza eguaglianza vale per la proprietà associativa. Dunque a''=a'.

Vi lascio verificare che l'insieme Z degli interi con l'usuale somma (Z,+) è un gruppo, anzi è un gruppo abeliano (commutativo). Così pure $\bg_white (Q- \begin{Bmatrix} 0\\ \end{Bmatrix},\cdot )$ ossia Q privato dello zero con l'usuale moltiplicazione è un gruppo abeliano. Per noi sarà più interessante trattare gruppi non numerici. Cominciamo dai gruppi simmetrici, in quanto lo studio dei gruppi partì proprio da qui. Prima un'altra definizione.

Sottogruppi

Se (G, °) è un gruppo, un sottogruppo di G è una struttura (H, °), dove H è un sottoinsieme di G, chiuso rispetto alla operazione ° definita in G e contenente $\bg_white e_{G}$ e l’inverso di ogni suo elemento. Si ha così che (H, °) è un gruppo e $\bg_white e_{H}=e_{G}$ .

I gruppi simmetrici

Dato un insieme A, consideriamo (tutte)le funzioni biunivoche f: A--->A

(per un chiarimento dettagliato sulle funzioni biunivoche vedere l'articolo sulla definizione di numero cardinale)

Chiamiamo $\bg_white S_{A}$ l'insieme di queste funzioni biunivoche. Prendiamo adesso come operazione tra due funzioni °: $\bg_white S_{A}$ X $\bg_white S_{A}$ ---> $\bg_white S_{A}$ , la composizione di due funzioni biunivoche f,g. f°g è una funzione che è anch'essa biunivoca, quindi l'operazione ° è una operazione interna.

Se ho tre funzioni f,g,h ovviamente è indifferente applicare f a g°h oppure f°g ad h; , infatti qualsiasi sia x, f°(g°h)(x) =f(g(h(x))=f°g(h(x)) quindi vale la proprietà associativa.

La funzione i che manda ogni elemento in se stesso (identità) è l'elemento neutro, in quanto se mandiamo un elemento a in b e poi applichiamo ancora i otteniamo ancora b; quindi componendo f con i ottengo f; lo stesso se compongo i con f.

Data una qualsiasi funzione f biunivoca, esiste la funzione inversa (potete verificarlo sempre QUI) che chiamiamo $\bg_white f^{-1}$ ; se componiamo $\bg_white \bg_white f^{-1}\cdot f=i$ , e anche se componiamo $\bg_white f\cdot f^{-1}=i$ ; quindi per ogni f esiste l'elemento l'inverso.

Quindi $\bg_white S_{A}$ è un gruppo. Non è un gruppo abeliano se il numero di elementi di A è maggiore o uguale a tre; se componiamo f°g in generale non otteniamo la stessa cosa di g°f

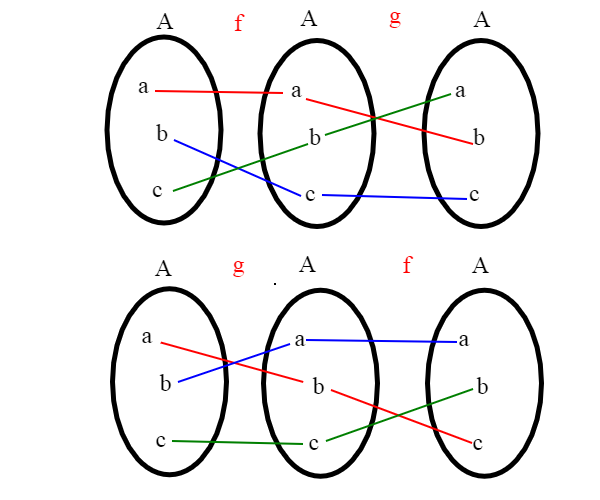
Le applicazioni biunivoche di un insieme A in se stesso si chiamano anche permutazioni; possiamo pensare infatti ad una applicazione biunivoca come ad una applicazione che sposta gli elementi di uno stesso insieme in posizioni diverse; se l'insieme è A={1,2,3,..n} i gruppi corrispondenti si denotano con Sn. Dalla definizione di fattoriale possiamo trovare l'ordine del gruppo Sn, che è uguale a n!. Infatti il fattoriale di un numero n altro non è che il numero di permutazioni di un insieme con n elementi.

Per rappresentare una permutazione $\bg_white \alpha$ in Sn, possiamo usare la scrittura:

$\bg_white \bg_white \bg_white \alpha =\begin{pmatrix} 1,\hspace{6mm} 2\hspace{6mm},3 \hspace{6mm},..n\\ \alpha (1),\alpha (2),\alpha (3)\hspace{6mm}..\alpha (n) \end{pmatrix}$

torniamo al caso n=2; usando questa rappresentazione, essendo 2!=2, esplicitiamo le due permutazioni:

$\bg_white \bg_white I=\begin{pmatrix} 1,2\\ 1,2 \end{pmatrix}$ (identità) e $\bg_white \tau =\begin{pmatrix} 1,2\\ 2,1 \end{pmatrix}$ se scriviamo una tabella per le composizioni possibili (qualcosa che ricorda la tabella Pitagorica), otteniamo:

°	I	$\bg_white \tau$
I	I	$\bg_white \tau$
$\bg_white \tau$	$\bg_white \tau$	I

Vediamo da qui che il gruppo S2 è abeliano.

IL GRUPPO DELLE ISOMETRIE PIANE

Il concetto di isometria.

Una isometria (dal greco ἴσος, isos, che significa uguale) è una nozione che generalizza quella di movimento rigido di un oggetto o di una figura geometrica.

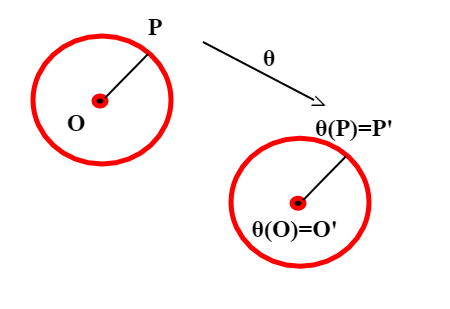
Consideriamo il piano Euclideo; se per isometria intendiamo una funzione che generi un movimento rigido, essa necessariamente conserva le distanze, e quindi applicata ad un ente geometrico, ne conserva la forma. Più in dettaglio, se Indichiamo con $\bg_white \mathbb{P}$ l'insieme dei punti de piano euclideo e con $\bg_white \theta$ una applicazione biunivoca $\bg_white \theta$ : $\bg_white \mathbb{P}$ ---> $\bg_white \mathbb{P}$ , diremo che $\bg_white \theta$ è un 'isometria se per ogni coppia di punti P,Q, chiamati $\bg_white \theta$ (P)=P' e $\bg_white \theta$ (Q)=Q' i punti corrispondenti, PQ=P'Q' (intendiamo con PQ la lunghezza del segmento con estremi P e Q).

iso1 — i segmenti PQ,P'Q' sono congruenti, perchè l'isometria conserva le distanze, o come preferite, genera un movimento rigido nel piano

Se consideriamo tre punti P,Q,R e $\bg_white \theta$ (P)=P', $\bg_white \theta$ (Q)=Q', $\bg_white \theta$ (R)=R' i due triangoli PQR e P'Q'R' sono congruenti avendo i tre lati uguali (terzo criterio). Essendo $\bg_white \theta$ un isometria;

iso2 — Una isometria trasforma un triangolo in un triangolo congruente, essendo i rispettivi lati congruenti. Se il triangolo degenera in un segmento, lo farà anche la sua immagine

Pertanto se R appartiene alla retta PQ anche R' appartiene alla retta P'Q'. Di conseguenza, ogni isometria trasforma rette in rette. Trasforma poi circonferenze in circonferenze dello stesso raggio; infatti se c è una circonferenza di raggio r, essa è il luogo geometrico dei punti equidistanti da un punto(centro) O, ossia i punti P del piano per cui PO=r; consideriamo allora l'immagine O'=θ(O) di O; se P è un punto di c, PO=r, ma allora P'O'=PO=r, quindi P'=θ(P) , immagine di P, appartiene alla circonferenza di centro O' e raggio r.

Chiamiamo H l'insieme delle isometrie.

H con l'operazione ° di composizione è un sottogruppo del gruppo delle biiezioni (applicazioni biunivoche) del piano in sé (in particolare H è un gruppo).
Dimostrazione.Dalla definizione di sottogruppo:

esistenza elemento neutro;Ovviamente, I∈H. (l'identità conserva le distanze, ovvero è una isometria).
La composizione di due isometrie è una isometria. Siano f, g∈H e siano P, Q due punti. Posto P' = f(P), Q' = f(Q), P" = g(P'), Q" = g(Q'), si ha P"Q" ≡ P'Q', perché g è un'isometria, P'Q' ≡ PQ, perché f è un'isometria, quindi P"Q" ≡ PQ. Ma allora anche g°f, che trasforma P in P" e Q in Q", è un'isometria.
L'inversa f di una isometria è una isometria. Se f manda P in P' e Q in Q', essendo PQ ≡ P'Q', anche f-1, che porta P' in P e Q' in Q, è un'isometria.

(chiaramente la proprietà associativa è vera per definizione, perchè una isometria è anche una applicazione biunivoca, e per le applicazioni biunivoche è valida).

Ci fermiamo qui come esempi di gruppi; visto che sono state ampiamente trattate in questo sito, mi piacerebbe se qualcuno provasse a verificare che le trasformazioni di Lorentz (con l'operazione di composizione) formano un gruppo. Questo fa capire come la struttura di gruppo sia applicabile anche alla fisica.

1 commento

Umberto

12/11/2016 at 17:38

C'è qualcuno che vuole provare a dimostrare che le trasformazioni di Lorentz (con l'operazione di composizione) formano un gruppo? Altrimenti non posso andare avanti, e dovrei farlo io.