Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Per dimostrare  il lemma di Zorn, abbiamo bisogno di un nuovo oggetto, le f-catene che sono un particolare  tipo di catene  che si definiscono a partire da una funzione di scelta, la cui esistenza è assicurata dall'assioma della scelta. Il nostro scopo finale è usare queste f-catene nel caso ammettano sempre almeno un maggiorante, per dimostrare che l'insieme che le contiene ha un elemento massimale.

f-catene

Dato un insieme P, consideriamo l'insieme delle parti di P. Sappiamo , grazie all'assioma della scelta, che esiste una funzione che associa ad ogni sottoinsieme di P , un suo elemento

 

Sappiamo che esiste almeno una f che fa questo; fissiamone una.

Consideriamo un sottoinsieme A di P; diremo che a è una f-catena se:

1. A è un insieme ben ordinato (è una catena).
2. Qualsiasi sia il segmento iniziale di A, (quindi qualsiasi sia ) consideriamo l'insieme   dei maggioranti stretti  del segmento ={x<a, x in A}, cioè i p maggiori di qualsiasi elemento di , ={p in P tali che p>}.(1) Se A è una f-catena, deve valere la condizione f()=a.

 

1. (la scrittura p>  significa che i p sono maggiori di qualsiasi elemento di )

Questa definizione di  f-catena può sembrare un po' strampalata, e troppo formale . Vediamo a cosa serve .  Quello che dobbiamo dimostrare è il lemma di Zorn:

Se P è un insieme parzialmente ordinato e se ogni sottoinsieme totalmente ordinato (catena)  di P ha maggiorante, allora P ha un elemento massimale.

L'idea  alla base di tutto, visto che abbiamo un insieme che è solo parzialmente ordinato, è di costruire una catena (che altro non è che un insieme ben ordinato) il più lunga possibile; supponendo di avere dei maggioranti stretti come nelle ipotesi del lemma, ciò si ottiene aggiungendo un elemento alla volta, scelto (tramite la funzione di scelta) fra l' insieme dei maggioranti (è necessario l'assioma della scelta). Otteniamo così una f-catena (f-catena perchè dipende dalla funzione f).

Se f è una funzione di scelta, supponiamo di costruire una f-catena così; sia =f(P), ovvero l'immagine di tutto P; A={} è una f-catena; infatti  (abbiamo un solo , ma nessun elemento di A è minore di  ), e  quindi P coincide con  (tutti gli elementi di P sono maggiori di quelli di , visto che non ha elementi); ma ; se  fosse un elemento massimale, non potremmo più andare avanti (però avremmo finito). In caso contrario, per la catena  {} abbiamo dei maggioranti;  consideriamo adesso i maggioranti di {}, ovvero M= {} e sia =f({}); > e inoltre l'insieme {,} è ancora una f-catena; infatti la condizione 2) è verificata per a= (lo abbiamo visto sopra), per a= , ={po}, ={p>}, f()=f({p>})=. Se è massimale, abbiamo finito; altrimenti possiamo andare avanti ancora nella costruzione, perchè abbiamo dei maggioranti stretti (che non appartengono ad A) appartenenti a P.

In generale per iterare il procedimento possiamo fare così: data la f-catena A, la estendiamo con

3);

passando a ;chiaramente vale la 1) (l'insieme A' è totalmente ordinato) dobbiamo verificare la 2) per ogni ; se  è vero perchè A è una f-catena, ci resta da provarlo per ; ma  il segmento iniziale coincide con A e l'insieme dei maggioranti di tale segmento è  quindi  per la 3)  .

Quindi per iterazione costruiamo una catena  A={}; continuiamo finché abbiamo dei maggioranti stretti, allungando al massimo la catena. Quando non ci saranno più maggioranti stretti,  sarà un massimo  per la f-catena , e un elemento massimale per P.

Abbiamo giustificato la definizione di f-catena e il suo utilizzo nel lemma di Zorn in modo informale ; per chi vuole la dimostrazione rigorosa del lemma, la trova  in appendice.

Osservazione sui massimali di un insieme

Non è vero in generale che ogni insieme parzialmente ordinato debba contenere elementi massimali;  basta pensare all’ insieme X i cui elementi sono i sottoinsiemi finiti di N, ordinato rispetto all’ inclusione. Chiaramente nessun elemento di X è massimale, perché a ogni sottoinsieme finito di N posso aggiungere un elemento, ottenendo così un sottoinsieme che lo include, ma ancora finito. Infatti X non soddisfa alle ipotesi del lemma di Zorn : C = {{0}, {0, 1}, {0, 1, 2}, {0, 1, 2, 3}, . . . } è una catena che non ammette alcun maggiorante in X.  In effetti, un sottoinsieme di N che contenga tutti tali sottoinsiemi (che sono tutti finiti) dovrebbe essere N stesso, che  non è un insieme finito, e quindi non è un elemento di X.

Applicazioni del lemma di Zorn

Nel prossimo articolo dimostreremo che il lemma di Zorn implica che  ogni insieme è ben ordinato,fatto noto come teorema di Zermelo; arriveremo così a dimostrare, grazie alla Tricotomia degli isomorfismi,  che due numeri cardinali sono sempre confrontabili, che non dimentichiamo, è il nostro obiettivo primario.

 

Appendice: dimostrazione rigorosa del lemma di Zorn

Due proprietà importanti delle  f-catene, che ci semplificheranno la dimostrazione del lemma.

Se A e B sono due f-catene, allora una è  un segmento iniziale dell'altra.

Visto che A e B sono buoni ordini, uno dei due è isomorfo ad un segmento iniziale dell'altro (per il teorema di Tricotomia  degli insiemi ben ordinati, visto nell'articolo predente).  Ad esempio, supponiamo che g : A --> S sia un isomorfismo, dove S è un segmento iniziale (non necessariamente proprio) di B. Vogliamo dimostrare che g è l'identità.

 

Se per assurdo g non è l'identità, allora non sempre i valori di g(x) sono uguali a x . Sia  ovvero il più piccolo elemento di A per cui questo succede(il minimo esiste perchè A è ben ordinato). Osserviamo due cose:  , se x<a g(x)=x, quindi sul segmento di A , g(x)=x; esistendo un isomorfismo che conserva l'ordine, se consideriamo l'insieme   che è un segmento iniziale di B, tale segmento coincide con .

Osserviamo innanzitutto, che se x=g(x), allora x appartiene sia ad A che a B; dobbiamo poi provare una doppia inclusione;

Se  , allora x<a; x=g(x)<g(a) essendo g isomorfismo. Dunque ;

se , x<g(a);  ma allora esiste a' tale che x=g(a'); a' <a  perchè g(a')<g(a); ma se a'<a, g(a')=a'=x, x=a'<a, quindi  x appartiene ad Aa, .

Ma se tali segmenti sono uguali, anche i maggioranti lo sono; ,  , contrariamente al fatto che abbiamo supposto 

 

L'unione C di tutte le f-catene di un insieme P è una f-catena . Essendo poi C unione di tutte le f-catene è l'f-catena massima.

Sappiamo che l'unione di un insieme di buoni ordini che sono un segmento iniziale dell'altro è ancora un buon ordine (lo abbiamo visto in  questo articolo. Abbiamo poi visto che date due f-catene, una è sempre segmento iniziale dell'altra (quindi sottoinsieme dell'altra) e quindi è ancora una f-catena.Supponiamo quindi che  sia l'unione di certi Ai, tutti f-catene. Qualsiasi sia , preso un segmento iniziale Cc  dobbiamo dimostrare che . Se  allora  per qualche A che compone l'unione. Sappiamo che A è una f-catena, quindi se Ac è il segmento iniziale corrispondente a c in A, . Vogliamo provare che  da cui seguirà ; se per assurdo i due insiemi non sono uguali, essendo , esisterà c'<c che sta in C ma non in A.

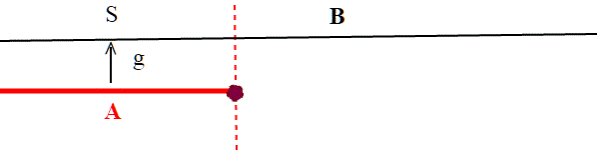
Tale c' dovrà appartenere a qualche B dell'unione, ma sappiamo che o A è segmento iniziale di B o viceversa; in entrambi i casi (vedi disegno) c' appartiene anche ad A.

(Ricordiamo la definizione di elemento massimale;Un elemento m appartenente ad  S si dice massimale se non esiste nessun elemento a appartenente ad ad S tale che m < a.)

Siamo pronti per dimostrare il lemma, di cui ripetiamo l'enunciato:

Lemma di Zorn: Se P è un insieme parzialmente ordinato e se ogni sottoinsieme totalmente ordinato (catena) di P ha maggiorante, allora P ha un elemento massimale.

Grazie ai risultati già elaborati sulle f-catene, la dimostrazione diventa relativamente immediata: sia C l'unione di tutte le f-catene di  S. Sappiamo che C è una f-catena, e quindi è la f-catena massima.  Non esistono maggioranti stretti di C (altrimenti la catena C potrebbe essere estesa). Da questo segue che un elemento maggiorante della catena C (che deve sempre esistere) è necessariamente il massimo di C, ed è inoltre un elemento massimale per P. Infatti se m è tale massimo, se non fosse massimale per P,  esisterebbe  n>m, n appartenente a P. Avremmo che l'insieme M dei maggioranti di C non è vuoto (contiene almeno n)e quindi la catena ottenuta estendendo (unendo) C con f(M)  (che è ancora una f-catena) sarebbe più grande di C, mentre sappiamo che C è l'unione di tutte le f-catene di P.