Cantor, parte 16°:Il lemma di Zorn 2/3

18/09/16

Cantor, parte 16°:Il lemma di Zorn 2/3

Categorie: Matematica Teoria degli insiemi Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Riprendo la definizione di isomorfismo data alla fine dell'articolo precedente. Questo articolo sarà completamente  dedicato alla dimostrazione di un importante teorema sugli isomorfismi, essenziale per la comprensione del lemma di Zorn.

Isomorfismi di buoni ordini

Siano dati due insiemi ordinati A e B e una funzione f : A---> B  crescente , ovvero x < y implica f(x) < f(y) per ogni x; y appartenente ad  A. Se f e anche biunivoca diremo che f e un isomorfismo . Ricordiamo che una funzione crescente è iniettiva, quindi basta che f sia suriettiva per essere biunivoca e per essere un isomorfismo. Non facciamoci spaventare da questa definizione:isomorfismo è una parola che deriva dal Greco ( ( ἴσος, isos, che significa uguale, e μορφή, morphé, che significa forma) ,e significa in pratica stessa forma; per i matematici due insiemi isomorfi nell'ambito di certe strutture praticamente sono la stessa cosa.

Esempio di isomorfismo: consideriamo i numeri naturali N e i  numeri pari P; entrambi sono insiemi ben ordinati ; l'applicazione f: N-->P che a n\rightarrow 2\cdot n è una applicazione crescente e copre tutti i numeri pari (è suriettiva). Quindi è biunivoca.

Restrizione di un isomorfismo

Un prosizione molto importante, che ci servirà nel seguito,è la seguente:

Sia h: A-->B un isomorfismo.  Per ogni a appartenente ad A, consideriamo la restrizione di h ad

A_{a}, h_{|A_{a}}: A_{a}\rightarrow B_{h(a)}  ; h è un isomorfismo tra il segmento iniziale di A generato da a  e il segmento iniziale di B generato da h(a) (la scrittura h_{|A_{a}} indica appunto  la restrizione di una funzione ad un sottoinsieme del dominio).

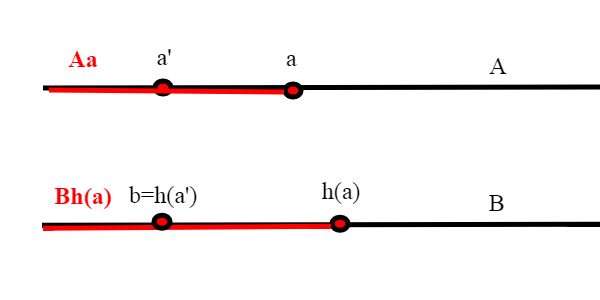
restrizione

Proviamo che h(A_{a}) = B_{h(a)}, ovvero che l'immagine del segmento A_{a} è uguale a B_{h(a)}, ovvero che h è suriettiva su B_{h(a)}

Basta dimostrare una doppia inclusione. Cominciamo da h(A_{a}) \subseteq B_{h(a)} ;essendo h crescente (x<a, h(x)<h(a)). Proviamo l'altra inclusione B_{h(a)}\subseteq h(A_{a}) ; prendiamo un b<h(a) ; h è suriettiva (stiamo considerando tutta la funzione h, da A-->B), quindi esiste a' tale che h(a')=b, e a'<a, perchè h è crescente.  Quindi  a'\in A_{a}.

Tre note preliminari, necessarie per la dimostrazione di un importante teorema sugli isomorfismi.

1)Se f: A-->A è un isomorfismo,( cioè se   a<a' implica f(a)<f(a')), allora f(a) >=a per ogni a\in A;)

Se per assurdo la tesi fosse falsa, esisterebbe x=min\begin{Bmatrix} a\in A: f(a)<a & \end{Bmatrix} (che è un sottoinsieme di A, ma A è ben ordinato). Ma allora f(x)<x, f(f(x))<f(x) quindi f(x)\in \begin{Bmatrix} a\in A: f(a)<a & \end{Bmatrix} contro il fatto che x è il minimo.

2)A non è isomorfo ad alcun suo segmento iniziale proprio.

Non possono esistere funzioni f: A ---> Aa che rispettano l'ordine, perchè si avrebbe f(a) \in A_{a}^{}, cioè

f(a) < a, contro la (1).

3) Segmenti iniziali propri diversi non sono isomorfi, cioè a\neq a' implica A_{a}\neq A_{a'}

se a\neq a' allora per esempio a' < a ;  possiamo considerare A_{a'} come un segmento iniziale dell'insieme (ben ordinato) A_{a} ; che  per la  2) non può essere isomorfo a A_{a'}.

Eccoci arrivati all'enunciato di un teorema molto importante sugli isomorfismi (anche detto Tricotomia degli insiemi bene ordinati)

Dati due buoni ordini A e B uno dei due è isomorfo ad un segmento iniziale dell'altro (non necessariamente proprio).

Indichiamo con   A\cong B due insiemi isomorfi

L'enunciato equivale a dire, che dati due insiemi ben ordinati A , B, ci possono essere tre possibilità:

  1. A\cong B
  2. A\cong B_{b}^{}\textrm{} (A è isomorfo ad un segmento iniziale di B)
  3. B\cong A_{a}^{}\textrm{} (B è isomorfo ad un segmento iniziale di A)

isomorismo

questo è un discorso molto simile a quello che vogliamo dimostrare sulla cardinalità degli insiemi; l'isomorfismo in fin dei conti è una applicazione biunivoca, che in più , nel caso di insiemi ordinati, conserva l'ordine. Il segmento iniziale di un insieme però altro non è che un sottoinsieme; dire che esiste una applicazione biunivoca di A in un segmento iniziale di B, vuol anche dire che esiste una applicazione biunivoca di A in un sottoinsieme di B (e questo nel caso dei cardinali significa che |A| <=|B|); se come anticipato  possiamo dimostrare che qualsiasi insieme si può ben ordinare, allora grazie a questo teorema avremo risolto il problema della confrontabilità dei cardinali.

Dobbiamo in qualche modo costruire una  funzione da A-->B che sia biunivoca e conservi l'ordine.  Definiamo un sottoinsieme di A x B in questo modo:

(ricordiamo che a volte per dare una funzione basta definire qual'è il suo  grafico)

Consideriamo una corrispondenza (un sottoinsieme di A x B) così definita:

G=\begin{Bmatrix} (a,b)\in A \times B : A_{a}\cong B_{b}\\ \end{Bmatrix}  (i due elementi corrispondono se esiste un isomorfismo fra i sottoinsiemi iniziali che definiscono ) questo è un sottoinsieme di A x B ; vogliamo dimostrare che è il grafico di una funzione F, che sarà l'isomorfismo cercato.

Dimostriamo per prima cosa che G è una funzione, ovvero che è univoca.

Se (a,b), (a,b') appartengono a G, alloraA_{a}\cong B_{b} e A_{a}\cong B_{b'}, quindi B_{b}\cong B_{b'} ( se esiste una applicazione biunivoca f fra A e B , e una g fra A e C  , ne esiste intanto una h fra B e A; allora componendo h con g otteniamo una applicazione biunivoca fra b e C). Abbiamo due segmenti iniziali di B isomorfi, necessariamente b=b'  per l'affermazione 3) delle note sopra ; quindi  G rappresenta proprio una funzione (è univoca, ovvero per un a abbiamo una sola immagine b) Possiamo allora chiamare F(a) l'immagine b di a.

1)Il dominio di F è un segmento iniziale di A

se b=F(a), alloraA_{a}\cong B_{b}\cong B_{F(a)}; esiste allora un isomorfismo h: A_{a}\rightarrow B_{F(a)} ; se a'<a,  possiamo considerare la restrizione di h su A_{a'}\rightarrow B_{h(a')} che è ancora un isomorfismo  (lo abbiamo visto sopra);perciò, oltre ad a, anche a' appartiene al dominio di F , dom(F). Quindi il dominio di F, chiamiamolo A'=dom(A) è un segmento iniziale di A (può anche essere tutto A,può infatti esistere un isomorfismo di A-->B per ogni elemento di A)

Inoltre F(a')=h(a')<b=h(a)=F(a) quindi  F è crescente.

2)L'immagine di F è un segmento iniziale di B.

Consideriamo ancora l'isomorfismo h:A_{a}\rightarrow B_{b}   ; se b'<b,sia a' l'elemento di di A tale che h(a')=b': consideriamo la restrizione di h :A_{a'}\rightarrow B_{b'}  che è ancora un isomorfismo. F(a')=b', quindi anche l'immagine di F è un segmento iniziale, stavolta di B. Chiamiamolo B'=imm(F) (che può essere tutto B per quello che ne sappiamo). Quindi F è un isomorfismo fra A' e B' (il dominio infatti è A' per definizione; la funzione è iniettiva perchè crescente, quindi è biunivoca sull'immagine B').

3) A' e B' non possono essere entrambi segmenti propri.

La funzione F è un isomorfismo fra un segmento iniziale A' di A è un segmento iniziale B' di B; Non può essere che A',B' siamo entrambi segmenti propri. Avremmo, se ciò fosse vero, un isomorfismoF:A_{a}\rightarrow B_{b} , e quindi (a,b) apparterebbe a G,  a apparterrebbe a dom(F)=A_{a}, b apparterrebbe a imm(F)=B_{b}, il che è assurdo. (a, b non possono appartenere ai segmenti A_{a} , B_{b}, che sono rispettivamente gli x<a, y<b)

Restano perciò le tre possibilità dell'enunciato del teorema:

  1. A'=A , B'=B ; quindi A\cong B
  2. A'=A, B'=B_{b}; quindi A\cong B_{b}^{}\textrm{} (A è isomorfo ad un segmento iniziale di B)
  3. A'=A_{a}, B'=B; quindi B\cong A_{a}^{}\textrm{} (B è isomorfo ad un segmento iniziale di A)

Siamo ora pronti per affrontare il lemma di Zorn; nel prossimo articolo applicheremo questo importante risultato ad un tipo particolare di insiemi ben ordinati; le f-catene.

 

Articoli correlati

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.