Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Questo è il primo di una miniserie di (tre) articoli dedicati unicamente al lemma di Zorn.

Per poter enunciare il lemma di Zorn, è necessario conoscere certe definizioni e certi risultati sugli insiemi ben ordinati. Ricordo che gli insiemi ben ordinati sono insiemi totalmente ordinati (ovvero insiemi in cui è possibile il confronto fra due elementi qualsiasi) in cui ogni sottoinsieme non vuoto ammette minimo.  Ne abbiamo visto un esempio: i numeri naturali. Invece gli insiemi Z, Q, R  pur essendo totalmente ordinati non sono ben ordinati, in quanto non tutti i sottoinsiemi hanno un minimo.Gli insiemi ben ordinati sono, per così dire, una "estensione teorica" dell'ordinamento dei numeri naturali.Se nei naturali esistevano concetti come il successivo,e l'induzione , in questi insiemi possiamo definire un successore e una sorta di induzione(induzione transfinita). Notiamo che un insieme ben ordinato non è detto che sia numerabile.

Proprietà e definizioni sugli insiemi ben ordinati.

Maggioranti di un insieme.

Dato un insieme A, chiamiamo b maggiorante di A se a<=b qualsiasi sia a appartenente ad A.

Segmenti iniziali

Dato un insieme ben ordinato A, definiamo segmento iniziale di A ogni sottoinsieme così definito:

dove a è un elemento qualsiasi di A; essendo l'insieme strettamente contenuto in A (a non appartiene ad ), il segmento iniziale si dice proprio.

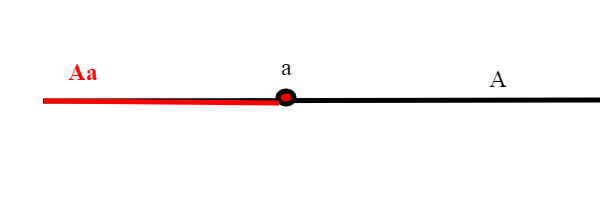
Quando in matematica si dà una definizione su un insieme(tipo quella di buon ordine) la prima cosa che si prova a fare è vedere se la definizione si conserva con le usuali operazioni, tipo l'unione. Non è però vero che l'unione di buoni ordini sia in generale un buon ordine ( vedi più sotto l'insieme delle parti, che non è totalmente ordinato ma può essere rappresentato come unione di insiemi totalmente ordinati) ma se aggiungiamo una condizione sui segmenti iniziali, allora si.

L'unione di un insieme (collezione,famiglia) di buoni ordini che sono uno un segmento iniziale dell'altro è ancora un buon ordine.

Supponiamo di avere una famiglia  (collezione) F di insiemi ben ordinati. Consideriamo l'unione di tali insiemi,  . X è totalmente ordinato; Dati a; b appartenenti a X, prendiamo A;B appartenenti a F tali che a appartenga ad  A e b appartenga B. Sappiamo che A è un segmento iniziale di B o viceversa;
sia vero per A; . Allora a,b sono confrontabili in B, e quindi nell'unione X.

Per vedere se X è un buon ordine, verifichiamo che ogni sottoinsieme Y di X ha minimo. Consideriamo ; supponiamo che non sia il minimo di Y, altrimenti avremmo già finito;  sia  tale che ;consideriamo adesso l'insieme degli  , che apparteranno a qualche B di F (). (In pratica ogni  apparterrà a qualche B  della famiglia, essendo appunto X unione di questi insiemi).Sappiamo che A è un segmento iniziale di B o viceversa, in ogni caso x appartiene anche ad A. 

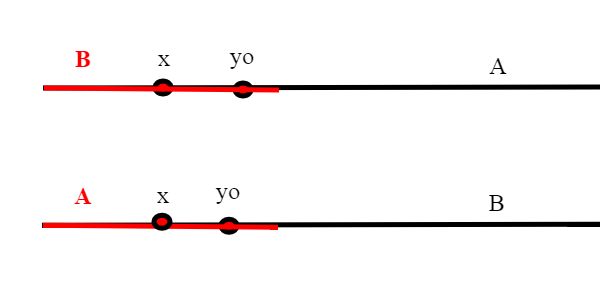
  e  quindi   (se vale per ogni x in X,allora vale senz'altro per quelli in Y), Ma A è un insieme ben ordinato, quindi Y' ammette minimo. E il minimo di Y in X coincide con il minimo di Y' in A (i minoranti infatti stanno tutti in A, come visto,e il minimo è il massimo dei minoranti).

Insiemi parzialmente ordinati

Qualora non tutti gli elementi di un insieme siano confrontabili si parla di insiemi parzialmente ordinati.

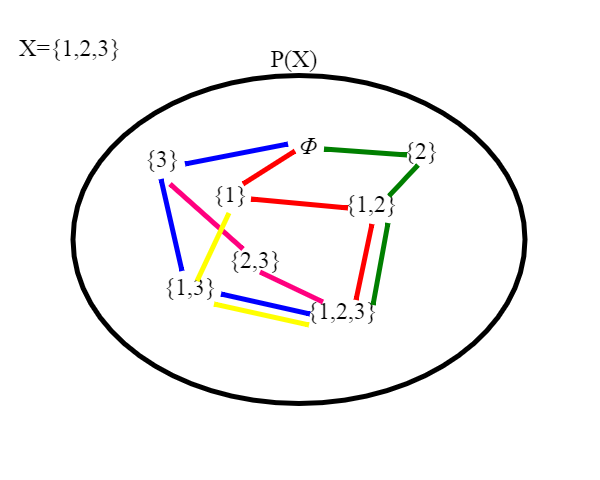
Un esempio di insieme parzialmente ordinato è l'insieme delle parti con l'ordine di inclusione; non tutti gli elementi sono confrontabili.

Elemento massimale

Un elemento m appartenente ad  A si dice massimale se non esiste nessun elemento a appartenente ad ad A tale che m < a.
Per un insieme A totalmente ordinato, le nozioni di elemento massimo ed elemento massimale coincidono, e sappiamo che il massimo è unico. Un insieme parzialmente ordinato può invece possedere più elementi massimali . Nell'esempio sopra di P({1,2,3}),  X={1,2,3} è evidentemente un massimo per P(X); se consideriamo invece P(X)\ {1,2,3}, ovvero togliamo {1,2,3} , abbiamo più elementi massimali, {1,2,},{2,3},{1,3}.

Catene negli insiemi parzialmente ordinati

Abbiamo visto che in generale in un insieme X parzialmente ordinato, non è detto che ogni elemento sia confrontabile con un altro elemento dell'insieme. E' però possibile che certi sottoinsiemi di X siano totalmente ordinati;

 

Se come esempio se  consideriamo l'insieme delle parti X=P({1,2,3} con l'ordine generato dall'inclusione,gli elementi di X   ,{1} {1,2}, {1,2,3} costituiscono un sottoinsieme totalmente ordinato di X. Tali sottoinsiemi prendono anche il nome suggestivo di catene. Se un sottoinsieme C di X è una catena, un elemento x di X si dice maggiorante di C se per ogni c di C, c<=x. L'elemento x può appartenere o no a C; nel caso non appartenga, x si dice maggiorante stretto.

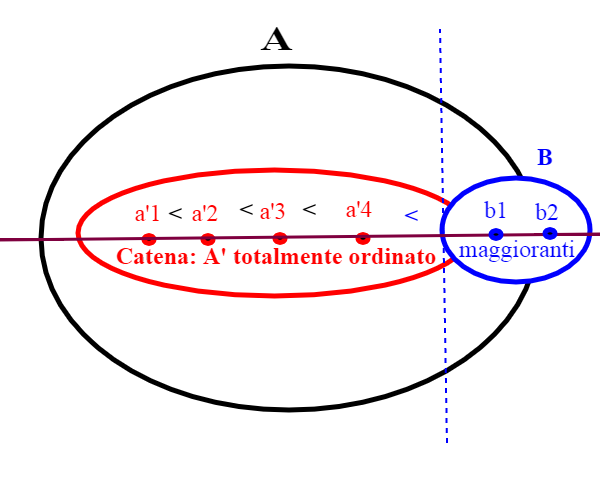
Vi chiedo un p0' di pazienza; per arrivare al lemma di Zorn sono necessari i concetti espressi  in questo articolo e nel prossimo. Se un insieme è ben ordinato, si fa presto a trovare elementi minimi e massimi. Se non lo è (e questo è il caso più generale) ,ma lo è solo parzialmente, dobbiamo esplorarlo sfruttando dei sottoinsiemi ordinati, che che abbiamo chiamato catene.

La prossima volta ci occuperemo di isomorfismi fra buoni ordini. Dò solo la definizione di isomorfismo, quale introduzione al prossimo articolo.

Isomorfismi di buoni ordini

Siano dati due insiemi ordinati A e B una funzione f : A---> B  crescente , ovvero  x < y implica f(x) < f(y) per ogni x; y appartenente ad  A. Se f e anche biunivoca diremo che f e un isomorfismo . Ricordiamo che una funzione crescente è iniettiva, Quindi basta che f sia suriettiva per essere biunivoca. Non facciamoci spaventare da questa definizione:isomorfismo è una parola che deriva dal Greco ,e significa in pratica che due cose hanno la stessa forma; per i matematici due insiemi isomorfi nell'ambito di certe strutture praticamente sono la stessa cosa