Il primo è stato discusso da vari lettori che sono arrivati in fretta alla soluzione. Il secondo è stato risolto brillantemente dal solo Arturo (un vero matematico!).

(1) Due fette uguali ma strane

I due punti M e N possono trovarsi ovunque lungo i due lati. Infatti, se dipingiamo di verde i due triangoli della Fig. 1, abbiamo che il triangolo formato dal pezzo rosso e da quelli verdi (ABN) ha un’area uguale a metà di quella del quadrato (base per altezza diviso 2 = lato per lato diviso 2).

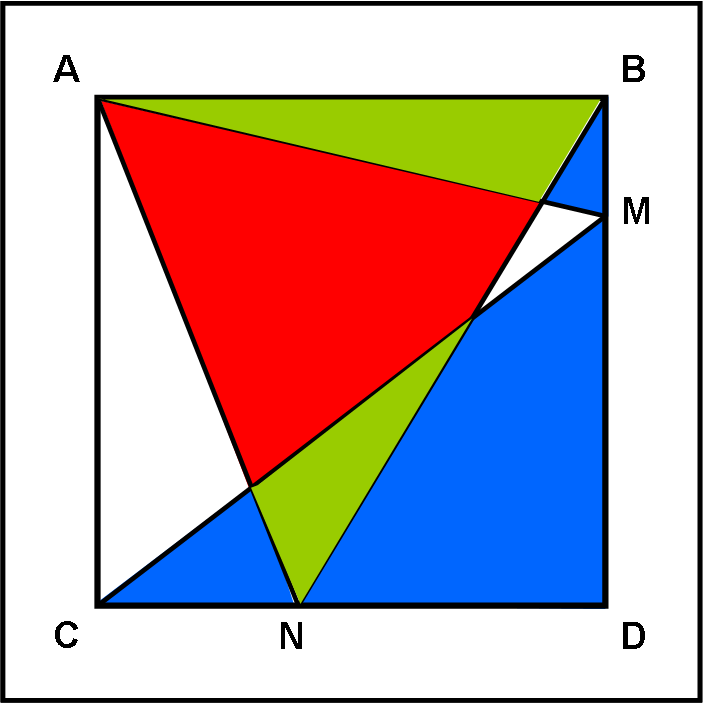
Ma anche il triangolo AMC ha la stessa area e quindi ciò che rimane (area della figura azzurra e verde) deve avere la stessa area, ossia la metà di quella del quadrato.

La parte azzurra e quella rossa hanno quindi la stessa area dato che a due aree uguali viene sottratta la stessa quantità (i due pezzi verdi). E questo vale sempre, qualsiasi siano i punti M e N.

(2) Semplifichiamo le cose complicate

Ottima la risposta di Arturo. C’è poco da aggiungere…

Il termine generico può essere scritto:

k/(k + 1)! = ((k +1) -1)/(k + 1)! = (k + 1)/(k + 1)! -1(k + 1)! = 1/k! – 1(k+1)!

per k = 1      si ha: 1 –1/2!

per k = 2     si ha: 1/2! – 1/3!

sommandoli  si eliminano i termini uguali di segno opposto. Continuando così via fino al termine k = n-1, che vale:

1/(n-1)! - 1/n!

Ci rimane soltanto:

1 - 1/n!

Che, giustamente, al tendere di n a infinito, tende a 1.

Più semplificato di così...

I quiz si trovano QUI e QUI