Categorie: Curiosità Matematica
Tags: giochi Maga dei Numeri matematica numeri quiz Valentina
Scritto da: Valentina
Commenti:13
La Maga dei Numeri - 1° puntata
Ciao a tutti!
Innanzitutto mi presento: mi chiamo Valentina, ho 17 anni, frequento il quarto anno del liceo scientifico e mi diverto a giocare con i numeri… mi diverto talmente tanto che, a volte, la mia testa ci gioca da sola senza che me ne renda conto finché, all’improvviso, si decide a far giocare anche me e mi “appaiono” davanti agli occhi delle regole o delle espressioni fino a quel momento sconosciute (almeno per me).
Zappi (é così chiamo il professore) mi ha proposto di condividere con voi queste “apparizioni” e lo farò volentieri: magari insieme scopriremo che a qualcuna ci aveva già pensato qualcun altro oppure che altre sono originali e potremo divertirci a trovare una dimostrazione generale che dia loro un senso matematico compiuto, oppure a trovarne i limiti o possibili varianti… vedremo, l’importante è divertirsi!
Però non aspettatevi troppo dalla sottoscritta, non dimenticate che non ho ancora finito il liceo e mancano ancora molte frecce al mio arco matematico!
Ma prima di proporvi la prima “apparizione” vorrei raccontarvi come sono nati i numeri… questa non è farina del mio sacco, si tratta di una storiella che ho letto in un libro (“Il mago dei numeri” di H.M. Enzensberger), nel quale un ragazzino supera la sua paura della matematica grazie ad incontri onirici con il mago dei numeri. Durante il primo incontro, per dimostrare a Roberto quanto i numeri siano “magicamente” semplici e stimolare la sua curiosità, il mago gli spiega come sono nati: per cominciare basta solo l’uno
1 x 1 = 1
Per far nascere il 2, non dobbiamo fare altro che moltiplicare per se stesso il numero 11 ovvero “2 volte 1”
11 x 11 = 121
Per fare la conoscenza con il 3, chiederemo aiuto al numero 111 (3 volte 1)
111 x 111 = 12321
Moltiplicando per se stesso 1111 (4 volte 1), facciamo nascere il 4
1111 x 1111 = 1234321
E così via…
Come avrete notato, oltre alla magia della nascita dei numeri, abbiamo anche la magia della palindromia: questi numeri si possono leggere indifferentemente sia da destra che da sinistra!
Per me questa storiella è una specie di droga e, ogni volta che ci penso, mi meraviglio sempre di più! Al punto che ho fatto alcune prove con combinazioni diverse di 1 e ho scoperto che se si moltiplica “3 volte 1” per “4 volte 1” non ce la facciamo a far nascere il 4 (manca un 1) ma si ottiene un numero molto simile a quello che avrebbe fatto nascere il 4 al quale, però, manca solo il... 4
111 x 1111 = 123321
Non è difficile capire come funziona questo meccanismo e non abbiamo bisogno della calcolatrice per il caso del 6 mancato!
11111 x 111111 = 1234554321
Chissà se qualcuno di voi riuscirà a trovare qualche altra regola ricorrente lavorando con l’uno…
Ma veniamo, finalmente, alle “cose serie” (si fa per dire!): non chiedetemi come ho fatto, ma mi sono accorta che, se sommiamo numeri interi progressivi, a partire da 1, tutti elevati al cubo, il risultato coincide con il quadrato della loro sommatoria, ovvero
![]()
![]()
Tutto bello, ma mi piacerebbe capire se questa formula ha carattere generale, quindi vi chiedo di aiutarmi, sempre che sia possibile, a dimostrare che
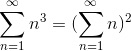
ovvero, visto che il secondo membro non è altro che la sommatoria di Gauss, dobbiamo dimostrare che
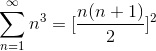
è verificata per ogni numero naturale.
Buon divertimento!
QUI trovate la dimostrazione completa
QUI trovate tutte le puntate de "La Maga dei Numeri"






13 commenti
Benvenuta tra noi Valentina!
Penso che questo quiz sia tagliato a misura per Umberto (Umberto, non scatenarti subito!!! )
)
penso che tutti possano risolverlo facilmente usando il principio di induzione
comunque molto interessante Valentina
attenzione però a quella sommatoria col simbolo di infinito: Diventa la somma di una serie che però non è convergente, ovvero non dà un numero.. Resta comunque vero che é valida per ogni ñ
Sul "facilmente" (almeno per me) qualche dubbio ce l'ho...
hai ragione, diciamo"abbastanza" facilmente; bisogna conoscere il principio di induzione e applicarlo correttamente.
...principio che proprio tu, Umberto, hai spiegato QUI
si, grazie mille!
Benvenuta Valentina. Un ottimo esordio!
Grazie per aver descritto il gioco di prestigio del mago... è davvero molto interessante e divertente (non lo conoscevo
(non lo conoscevo  ).
).
Paolo
Un tentativo di dimostrazione è quello che ci vuole per finire questa domenica in compagnia di questo Circolo.
a) La (1) è vera per n=1. Infatti, per n=1 risulta:
b) Se la (1) è vera per n, è vera anche per n+1 ? Vediamo.
Cioè ho ottenuto:
quindi la (1) è vera anche per n+1.
Allora, essendo verificate le condizioni a) e b), per il principio di induzione, la (1) è vera per qualunque valore di n. (se non ho sbagliato qualche cosa vista l'ora tarda )
)
A domani e buon inizio di settimana a tutti.
mamma mia, che piacere vedere questa rapidità e questa signorilità... Grazie a Umberto che non ha infilato subito il coltello nella ferita (e poteva farlo con facilità estrema) e grazie ad Arturo che mostra il suo divertimento puro e quasi infantile (che bello sarebbe essere tutti bambini nell'anima e nel cuore, qualsiasi cosa essi vogliano dire). Dopo un palloncino che vola ecco una dimostrazione ineccepibile. Siamo quasi tornati ai tempi degli antichi greci ( e non è una riduzione, anzi....). Non per niente il quiz prende proprio il nome di teorema di Nicomaco (l'ho scoperto da poco... ammetto!).
Ricordiamo anche che la sommatoria di Gauss si dimostra anch'essa per induzione.
Insomma grazie a tutti, Valentina per prima, che si divertono facendo girare la mente!!!!
La mia presenza qui diventa sempre meno importante (ma qualcosa la farò ancora!!!!) e questo non può che riempirmi di gioia

Un po' mi dispiace che questo Nicomaco ci avesse già pensato...
Comunque sono contenta di sapere che l'uguaglianza è sempre verificata. Ora purtroppo devo scappare a scuola perché mi aspetta un terribile compito di storia, ma, appena possibile, studierò la dimostrazione.
Grazie a tutti!
Si, la sommatoria di Gauss era stata dimostrata nel l'articolo sull'induzione matematica
Grazie a te Valentina !
Dal quarto anno di liceo scientifico ci sono ripassato due anni fa , con mia figlia. Trigonometria, che passione....