Quiz: appoggiamo una trave ***
Eccoci a un bel problemino geometrico-matematico. In fondo, però, si tratta solo di trovare la relazione tra due angoli… una cosa da ridere (?). Forza…
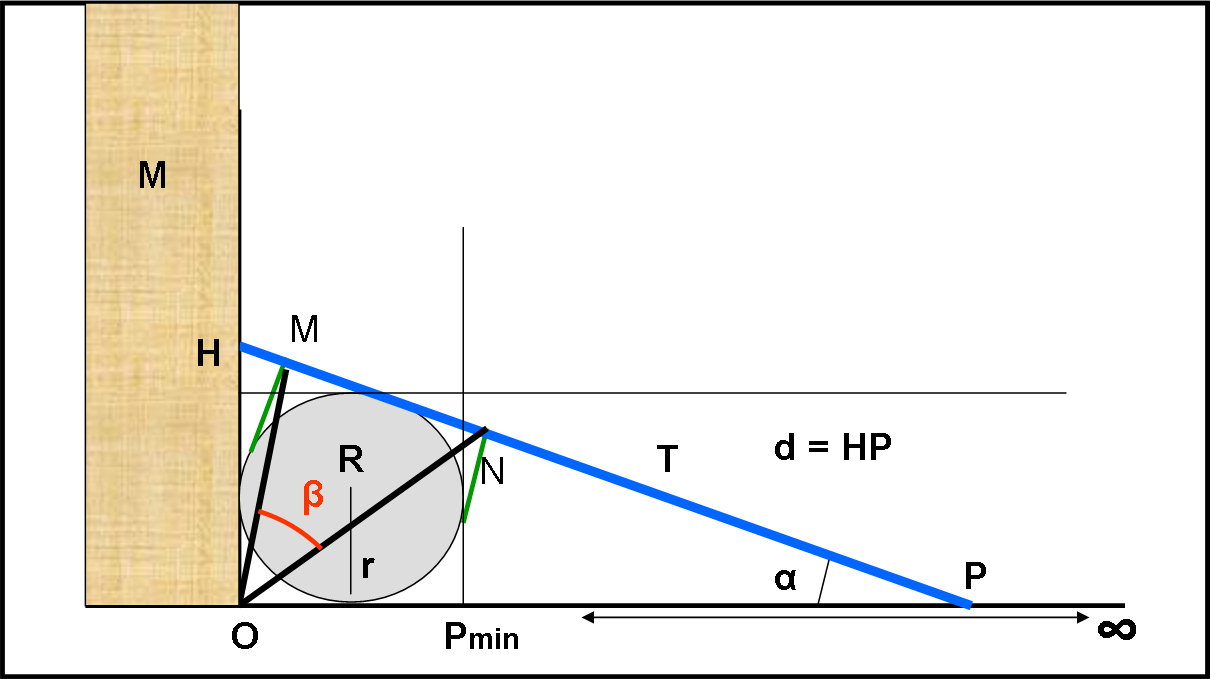
Un muro M è poggiato in modo perfettamente perpendicolare al terreno. Lo ipotizziamo di altezza infinita. Contro di lui si spinge una ruota circolare R di raggio r. A questo punto, si appoggia alla ruota una trave T, di lunghezza d, che vada a toccare il muro M nel punto H. Proiettiamo la ruota sulla trave. I punti di contatto siano M e N. O sia il punto alla base del muro M. Il punto di contatto della trave con il terreno sia P.
Facciamo variare il punto P (la sua posizione può variare, al limite, da Pmin fino a ∞). Cambia di conseguenza anche la lunghezza d = PH della trave. Chiamiamo α l’angolo tra la trave e il terreno, anch’esso variabile.
La domanda è: “Determinare come varia l’angolo β (MON) in funzione dell’angolo α, fissando una volta per tutte il raggio r della ruota R. Trovare ovviamente anche il suo valore minimo e massimo”...
Forza e coraggio… potrebbe risolvere il problema anche quello scanzonato di Scherzy (se si impegnasse seriamente almeno una volta…).
QUI trovate la soluzione
12 commenti
Il segmento MN è lungo 2R e giace sulla circonferenza centro C e raggio CM = CO.
/2 (90 gradi).
/4 (45 gradi).
Il triangolo MCN è un angolo al centro della circonferenza suddetta ed ha base MN= 2R
e altezza R. Esso vale dunque
Il triangolo MON forma un angolo "alla circonferenza" nel punto O e quindi vale la metà
Non vi è dipendenza da alfa per tutte le posizioni della trave da orizzontale a verticale e non dipende nemmeno dalle dimensioni della ruota .
Leandro... mi dimostreresti perché O dovrebbe stare sul cerchio di centro C e raggio CM? In altre parole, perché CO è uguale a CM?
Posso dirlo?
andate tranquilli... siete sempre più bravi o sono io che non sono più alla vostra altezza? Temo la seconda (anche perché mi ha scritto in privato Arturo dandomi la soluzione esatta). I miei trucchetti vi hanno fatto un ... baffo!
Evviva il Circolo!!!!
se la trave è orizzontale il quadrato MNPO è inscritto nel cerchio grande e circosrive l ruota.
Il raggio del cerchio grande è![R\sqrt[2]{}](http://latex.codecogs.com/gif.latex?R\sqrt[2]{})
![\sqrt[]{2}](http://latex.codecogs.com/gif.latex?\sqrt[]{2})
, sia calcolato dalla proiezione sulla trave che considerando la sola ruota. Al muovere di alfa la proiezione dela ruota sulla trave fa ruotare rigidamente il quadrato intorno al centro comune. Poiché simmetrie assiali mantengono la congruenza niente cambia nelle proporzioni della figura e quindi rimane costante anche l'angolo beta.
O anche: il quadrato che circoscrive il cerchio R è di lato MN, O è il vertice di uno dei quadrati possibili.
OK!
Bene , bene, visto che si sono aperte le danze alla grande, eccomi qui con un mio contributo.
Quella che riporto di seguito è la terza dimostrazione del fatto che l'angolo beta è sempre pari a 45°, a prescindere dal valore dell'angolo alpha.
Consideriamo la seguente figura:
Considero i triangoli MAC e NAC. Tali triangoli sono entrambi rettangoli, isosceli e tra loro uguali, perché AN=AM=r per costruzione, CA=r in comune e gli angoli MAC ed NAC entrambi retti. Quindi anche il lato MC deve essere uguale al lato NC.
Considero ora il triangolo OCG. Anche esso è rettangolo e risulta OG=GC=r. In pratica tale triangolo è uguale ai primi due, quindi deve essere OC=MC=NC. Posso pensare allora questi tre segmenti come raggi della circonferenza con centro in C e passante per i tre punti M, N e O, cioè la circonferenza circoscritta al triangolo MON. Adesso è immediato notare che l'angolo MON è angolo alla circonferenza, mentre MCN è angolo al centro. In particolare l'angolo MCN = angolo MCA + angolo NCA = 45° + 45° = 90°. Allora, poiché l'angolo alla circonferenza è sempre metà di quello al centro sotteso da uno stesso arco (MN), ne deriva che beta = 90/2 = 45°
Evviva il Circolo !
Mamma mia... e chi vi tiene più!!! Nessuno è caduto nel trabocchetto... devo ancora aumentare la difficoltà... ma poi non sarò in grado di rispondere nemmeno io...
PADOVA. L’Università di Padova intitola il proprio Dipartimento di Matematica a Tullio Levi-Civita e lo celebra con un evento aperto al pubblico nell’Aula Magna di Palazzo del Bo venerdì 25 novembre alle 9.
LEGGI ANCHE:
Facoltà intitolata al matematico che corresse Einstein
Il Dipartimento del Bo porterà il nome di Levi-Civita, lo scienziato padovano “ucciso” dalle leggi razziali
Tullio Levi-Civita nasce a Padova nel 1873, dove diviene a soli 24 anni professore di Meccanica razionale, allievo di Gregorio Ricci Curbastro (Fisica matematica), Ernesto Padova, e Giuseppe Veronese (Geometria).
Scusate la disgressione,ma è una vera gloria di Padova e della nazione,altro che quaqquaraqqua vari dei nostri tempi!
Gianni mi fai emozionare,non tutti conoscono questi fatti. A noi lo hanno raccontato subito appena arrivati in facoltà, davanti alla statua che allora era in biblioteca. si, la R.G. ê anche italiana o meglio veneta, anche perché Hilbert era molto vicino ad una soluzione autonoma e senza il Civita e il suo maestro Ricci non si sa come sarebbe andata a finire