Innanzitutto, come dice giustamente Scherzy (una volta tanto siamo d’accordo… il mondo sta forse invertendo il senso di rotazione?), la risposta alla domanda: “Cosa dovete fare, mentre disegnate la stella, per far sì che la somma degli angoli di tutte e cinque le punte (A + B + C + D + E) sia esattamente uguale a  180°?”. Bene facilissimo… : “Niente!”.  A parte, ovviamente, tracciare la linea continua, senza mai fermarsi, e concludere la stella cinque punte. Qualsiasi stella otteniate in questo modo ha SEMPRE la somma degli angoli delle punte uguale a 180°. Vedremo, poi, come Maurizio sia riuscito a generalizzare il problema… Un articolo da leggere, perché è un esempio brillantissimo di come la collaborazione, impostata sul divertimento (e sulle capacità, ovviamente), riesca a dare informazioni sempre nuove e inaspettate.

Vincenzo

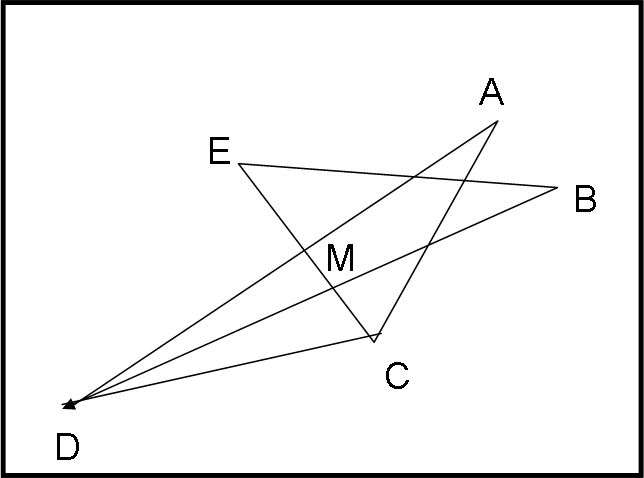
Congiungo le punte D e C della stella. Considero il triangolo DAC. L’angolo EMB è uguale a DMC. Ne consegue che la somma degli angoli della stella in E e B è uguale alla somma degli angoli MDC e MCD. La somma degli angoli alla base del triangolo DAC è allora uguale alla somma degli angoli della stella in E, B, C e D. Se sommo l’altro angolo del triangolo (angolo della stella in A) trovo proprio 180° (somma degli angoli di un triangolo).

In formule…

EMB = DMC

CEB + EBD= BDC + ECD

ADC = ADB +BDC

ACD = ACE + ECD

DAC + ACD + ADC = 180°

DAC + ACE + ECD + ADB + BDC = 180°

DAC + ACE + ADB + ECD + BDC = 180°

DAC + ACE + ADB + CEB + EBD = 180°

Valentina

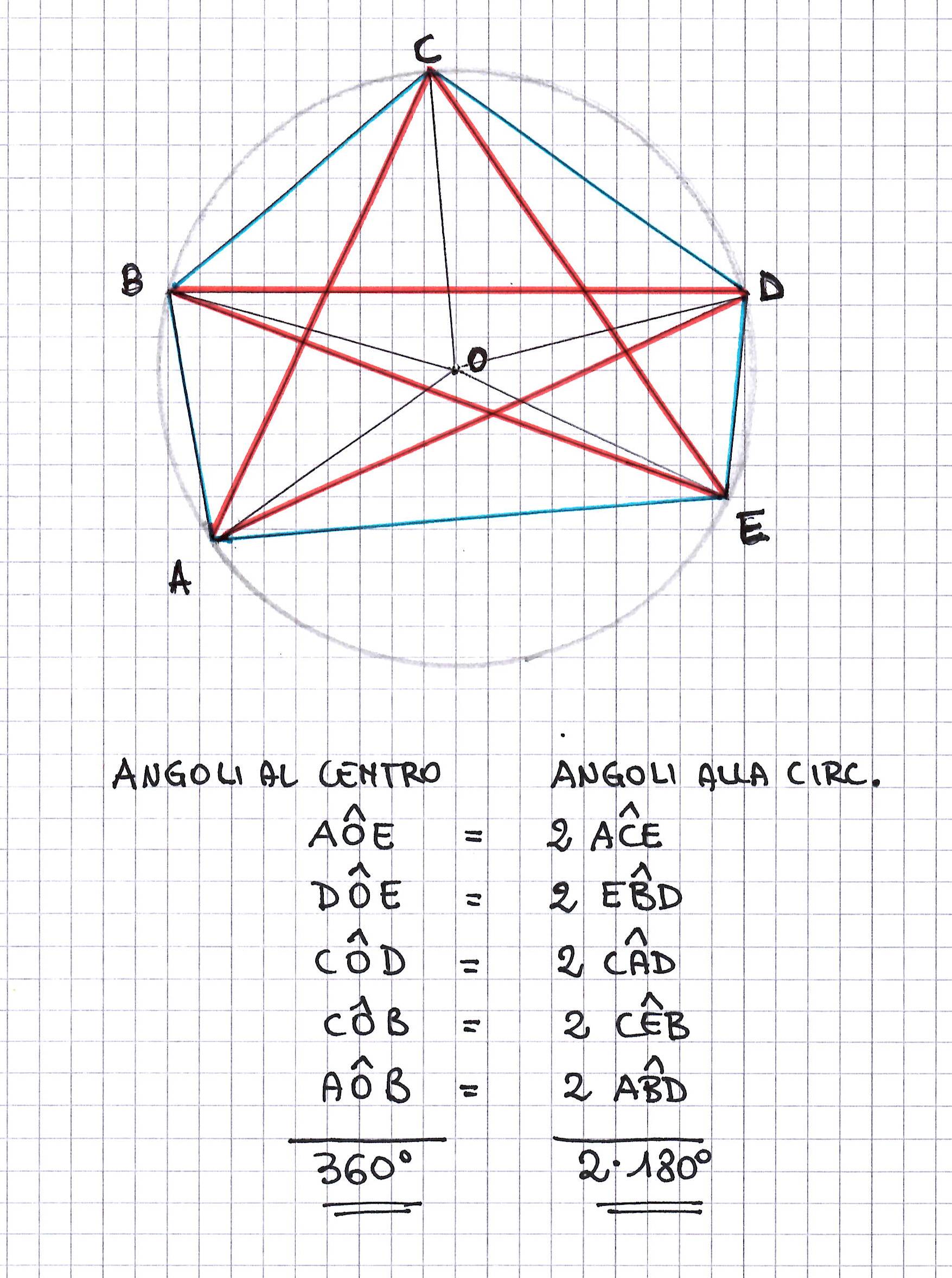
La sua prima soluzione è brillante, ma si riferisce solo a una stella inscrivibile in un cerchio. In tal caso basta sfruttare la proprietà che l’angolo al centro è doppio dell’ angolo alla circonferenza. Ossia: 360°/2 = 180°

 

Per cercare di tamponare la piccola imprecisione ha, inoltre, pubblicato un metodo che… più pratico non si può, come mostra la figura che segue:

 

Paolo Salvini

Parte subito con una bella soluzione grafica e delle chiare figure esplicative, che non hanno praticamente bisogno di spiegazione.

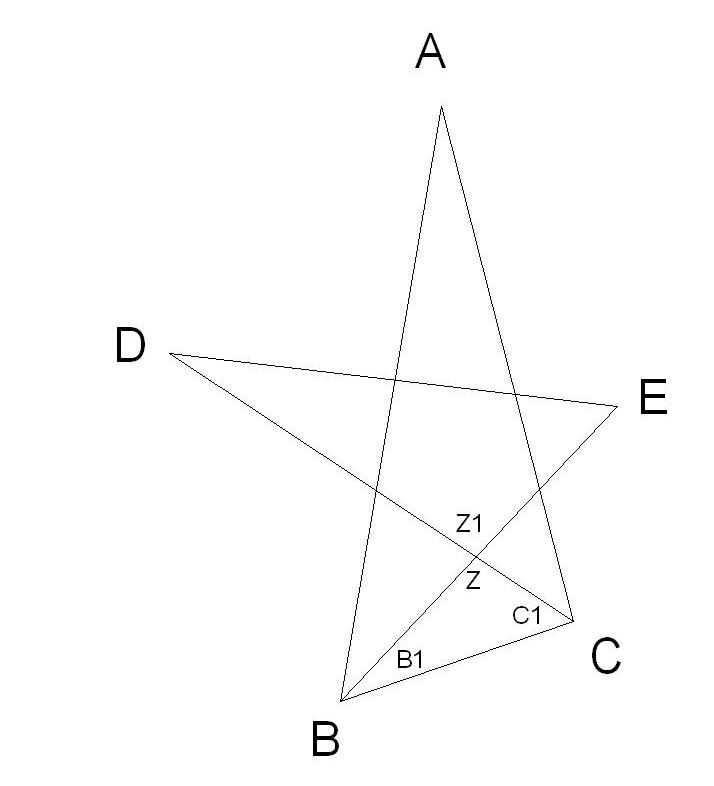
La somma  degli angoli interni del pentagono e' sempre di 540 ° (vedremo più tardi perché). Ora prendo i 5 triangoli che si formano inserendo una alla volta gli angoli del pentagono e le corrispondenti due punte della stella.

 

Ogni triangolo ha la somma degli  angoli uguale a 180° gradi. La somma degli angoli di tutti e 5 i triangoli e' 900°. Se tolgo da 900° la somma degli angoli appartenenti al pentagono (540°), ottengo 360°.  In questo approccio ogni punta compare due volte.  Per cui il risultato finale è proprio 360/2 = 180°.

Poi, non soddisfatto della bellissima, anche se un po’ lunga, costruzione si lancia in una splendida e contratta dimostrazione basata su un solo triangolo (splendida, anche perché è praticamente uguale a quella usata da Vincenzo… eh, eh, eh…).

Maurizio (Mauritius)

Parte al rallentatore, con una costruzione abbastanza farraginosa, ma poi si riscatta alla grande e generalizza il problema per una stella con un qualsiasi numero di punte. Confabulando con Valentina e con Vincenzo, arriva a un risultato estremamente compatto. Congratulazioni!

Innanzitutto, ricordo come si ottiene la formula che dà la somma degli angoli interni di un poligono qualsiasi. Basta sezionare il poligono con dei triangoli. Si vede che il numero dei triangoli è sempre uguale al numero dei lati del poligono meno due. Inoltre, la somma degli angoli del poligono è uguale alla somma degli angoli dei triangoli in esso contenuti, quindi:

 somma angoli interni poligono di n lati = 180 (n – 2)

 Passo al nostro problema.

Ai + Bi + Vi = 180

(180 – Pi) + (180 – Qi) + Vi = 180

360 – (Pi +Qi)  + Vi = 180

– (Pi +Qi)  + Vi = - 180

Vi = - 180 + (Pi +Qi) 

Sommando da 1 a n

∑ Vi = - n 180 + ∑Pi + ∑Qi

Ma

∑Pi = ∑Qi = 180 (n-2)

Sostituendo:

∑ Vi = - n 180 + 2 180 (n - 2) = - n 180 + 2 180 n – 4 180 = n 180 – 4 180 = 180 (n-4)

La formula ricorrente per qualsiasi n è:

∑ Vi = 180 (n – 4)

La formula funziona anche per il quadrato. Le punte delle stelle sono formate da rette parallele (ossia si incontrano all’infinito) e quindi la loro somma è uguale a ZERO. Per il triangolo abbiamo un risultato negativo, dato che le rette che dovrebbero formare le punte si discostano sempre più…

Arturo

Anche lui parte con una dimostrazione giusta, ma un po’ “impacciata”, che nemmeno riportiamo, dato che, poi, tira fuori dal suo cappello magico una soluzione geometrica ineccepibile ed elegantissima (e senza usare il palloncino...).

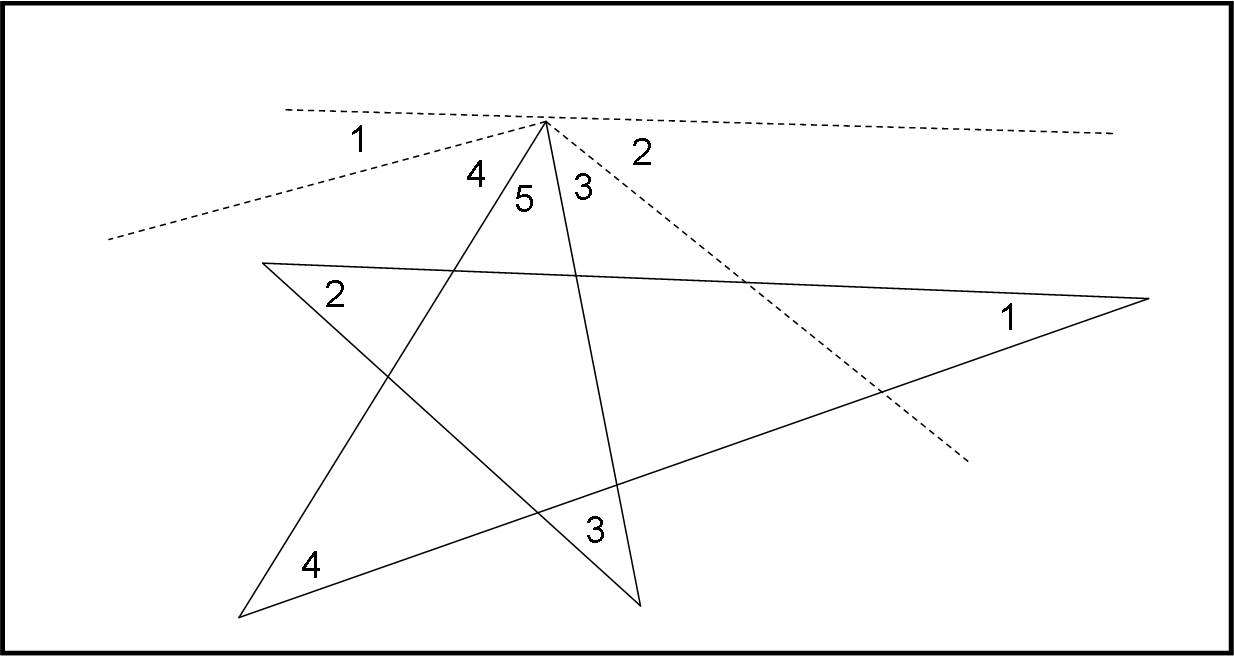
Prendo un vertice qualsiasi e traccio da lui le parallele alle linee della stella che non passano per quel punto. Basta lavorare con gli angoli di due rette parallele tagliate da una trasversale e si ottiene il risultato voluto…

Che dire? La collaborazione mirata a capire e a far capire, unita a una buona dose di ironia e umiltà, è sempre una ricetta insuperabile!

Il quiz lo trovate QUI