Categorie: Matematica
Tags: Club dei Maghi geometria quiz triangolo isoscele
Scritto da: Club dei Maghi
Commenti:3
Soluzione al quiz dell'angolo misterioso
Egr. sig. Oreste Pautasso,
siamo lieti di annunciarLe di essere riusciti a calcolare l'angolo che formano i raggi del Sole quando entrano in quella misteriosa piramide della quale gli archeofili di Cuneo hanno scoperto una raffigurazione in un'antica pergamena! Il bello è che lo abbiamo fatto senza bisogno di arrampicarci per misurarlo col goniometro, ma utilizzando quelle meraviglie che si chiamano matematica, geometria e trigonometria. E, siccome ci piace fare le cose per bene, abbiamo utilizzato metodi diversi per arrivare allo stesso risultato, così non avrà dubbi sul fatto che l'angolo calcolato sia proprio quello giusto!
Soluzione grafica
Questa soluzione richiede la conoscenza dei criteri di congruenza dei triangoli e di alcune caratteristiche fondamentali dei triangoli.
Consideriamo la figura del quiz:
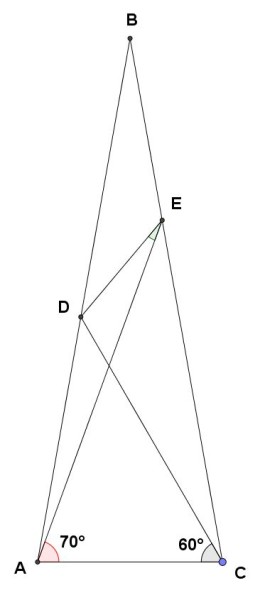
Tracciamo ora la retta per il punto D parallela alla base AC del triangolo isoscele e chiamiamo F il punto di intersezione tra tale retta e il lato obliquo BC del triangolo isoscele. Inoltre congiungiamo il punto A con il punto F e chiamiamo G il punto di intersezione tra tale segmento e il segmento DC . Per la simmetria assiale del triangolo isoscele ABC, il segmento AF risulterà inclinato di 60° rispetto alla base AC:
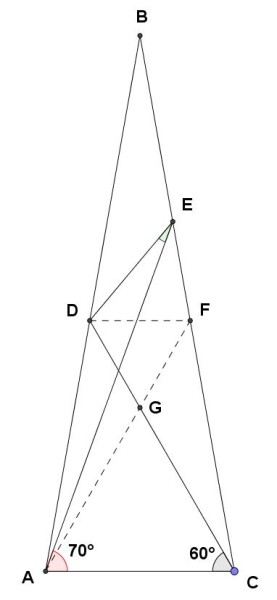
Sempre per la simmetria assiale del triangolo isoscele ABC, i due triangoli DGF e AGC sono equilateri.
Infatti, con riferimento al triangolo AGC, l'angolo AGC è pari a 60° perché i due angoli alla base GAC e ACG sono uguali e uguali entrambi a 60°. Quindi il triangolo AGC è equiangolo e quindi equilatero.
Con riferimento al triangolo DGF, l'angolo DGF è pari a 60° perché opposto al vertice dell'angolo AGC, che è appunto di 60°. Per la simmetria , i due angolo GDF e DFG devono essere tra loro uguali. Dovendo essere la soma degli angoli interni del triangolo DGF pari a 180 ° si ha allora che:
Pertanto, anche il triangolo DFG è equiangolo, quindi equilatero. Dunque sarà:
(1)
Consideriamo ora il triangolo ABG, che abbiamo evidenziato con il colore blu:
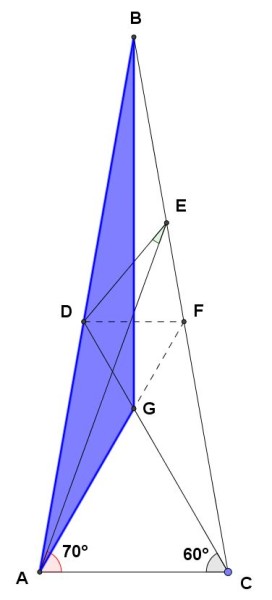
Gli angoli di tale triangolo sono tutti noti. Infatti:
Consideriamo ora il triangolo ABE, che abbiamo evidenziato con il colore verde:
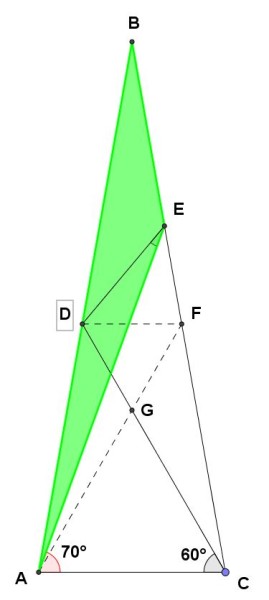
Gli angoli di tale triangolo sono tutti noti. Infatti:
Allora, con riferimento alla figura seguente, in cui sono evidenziati entrambi i suddetti triangoli:
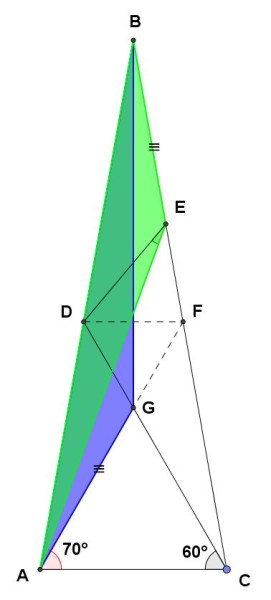
risulta che i due triangoli hanno il lato AB in comune e i lato omologhi angoli ad esso adiacenti tra loro congruenti. Pertanto, per il secondo criterio di congruenza dei triangoli, essi sono congruenti. Quindi avranno tutti gli elementi congruenti. In particolare:
(2)
Consideriamo, infine, il triangolo ABF, evidenziato in fucsia nella figura seguente:
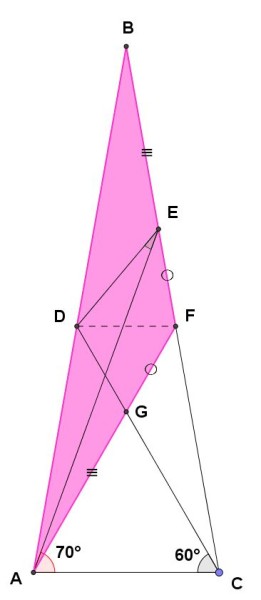
Questo triangolo è isoscele. Infatti :
Essendo isoscele, sarà
cioè, per la (2):
e quindi, per la (1):
Ma allora anche il triangolo DFE è isoscele, avendo i due lati DF ed EF congruenti.
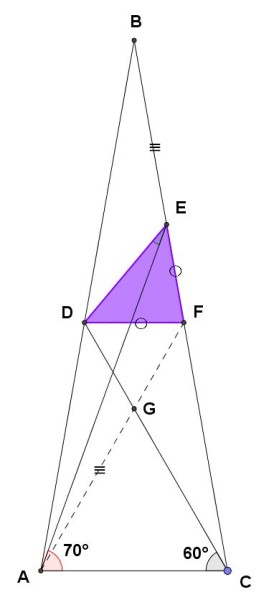
Essendo isoscele, i suoi angoli alla base DE sono congruenti, cioè, indicando con x l'angolo misterioso DEA e dovendo essere la somma degli angoli interni pari a 180°:
da cui, esplicitando rispetto alla x, otteniamo:
Soluzione analitica 1 (trigonometria)
Questa soluzione richiede la conoscenza del teorema dei seni. Consideriamo il triangolo DEA , evidenziato in blu nella seguente figura (la numerazione delle figure ricomincia ora da 1):
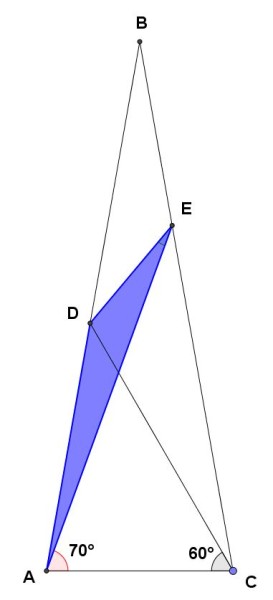
Per il teorema dei seni risulta, indicando con x l'angolo misterioso:
da cui, esplicitando rispetto ad AD e sostituendo i valori degli angoli noti:
(4)
Ora consideriamo il triangolo DEC, evidenziato in verde nella seguente figura:
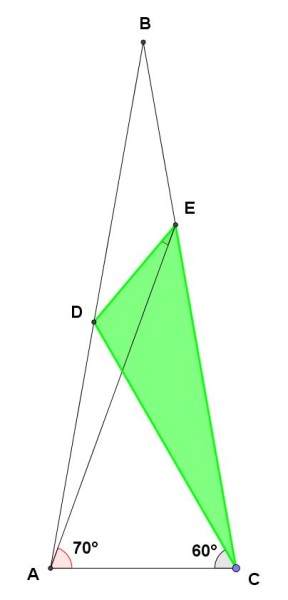
Sempre per il teorema dei seni risulta:
da cui, esplicitando rispetto a DC e sostituendo i valori degli angoli noti:
(5)
Infine, consideriamo il triangolo ADC, evidenziato in rosso nella seguente figura:
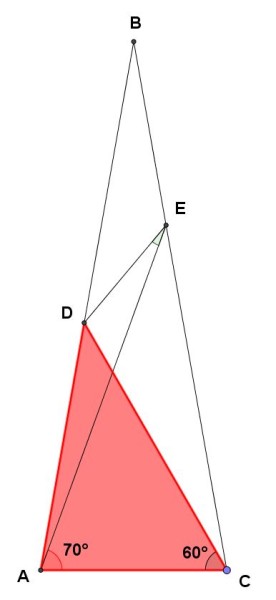
Ancora per il teorema dei seni risulta:
Sostituendo ora nella suddetta equazione le espressioni di AD e DC trovate rispettivamente con la (4) e la (5) otteniamo:
(6)
Per non portarci dietro i termini ai denominatori, definiamo il parametro
(il valore è noto ed è 2.23976411351 )
La (6) così diventa:
cioè, svolgendo il seno della somma al secondo termine:
cioè
moltiplico primo e secondo membro per 2, porto tutto a primo membro e sommo i termini simili:
Equazione lineare in seno e coseno risolvendo la quale, dopo avere sostituito a k il suo valore, otteniamo:
x=20 °
Soluzione analitica 2 (geometria analitica)
Questa soluzione, basata su considerazioni di geometria analitica, è quella proposta da Paolo nel suo commento al quiz. Paolo l'ha esposta in maniera così esauriente che ci sembra superfluo replicarla qui. Potete leggerla direttamente QUI.
Cosa succede se cambia l'inclinazione dei lati obliqui del triangolo
Questo quiz e il suggerimento di Vincenzo ci hanno fatto sorgere la curiosità di vedere cosa succede all'angolo misterioso al variare dell'inclinazione dei lati obliqui del triangolo isoscele ABC.
A questo proposito vi proponiamo questa animazione realizzata con Geogebra. Il valore iniziale dell'angolo di inclinazione dei lati obliqui è 80°, come da figura del quiz, e va crescendo fino a 90°.
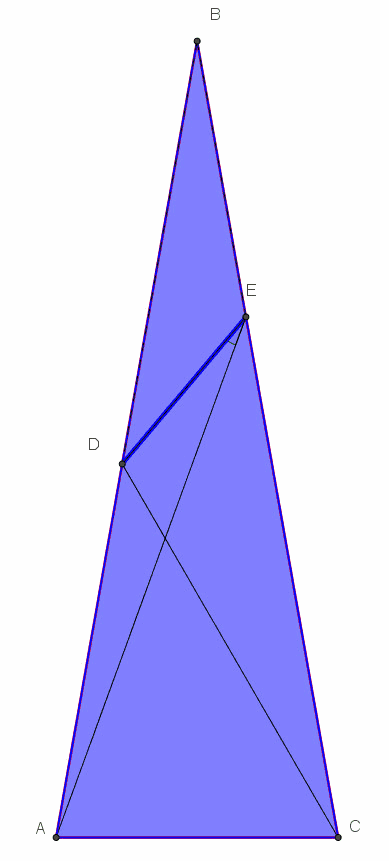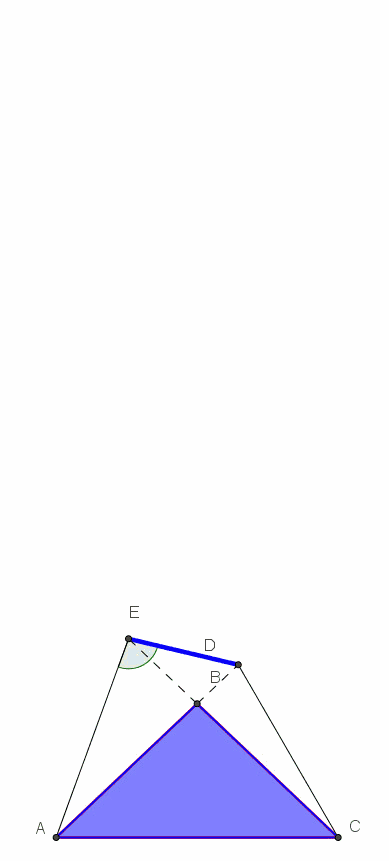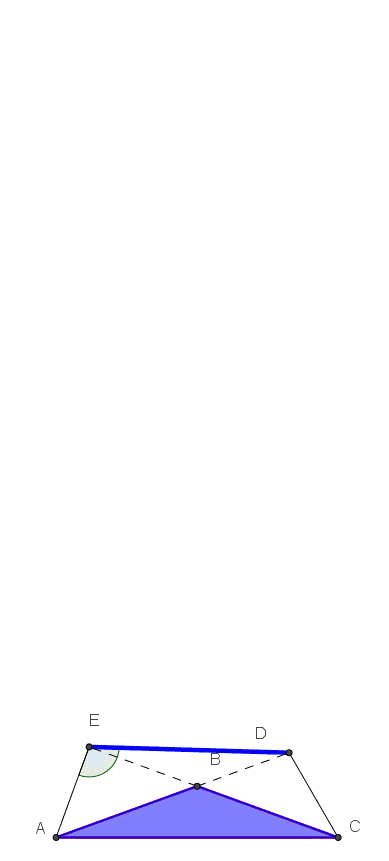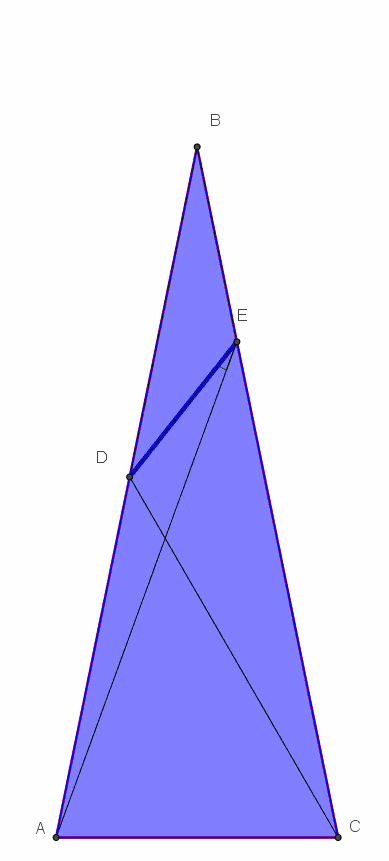
E' evidente che per inclinazione pari a 90° il triangolo diventa un rettangolo degenere, di base uguale a quella del triangolo isoscele di partenza e altezza di lunghezza infinita. L'angolo misterioso corrispondente a questa situazione è pari a 24,6°.
Una volta che l'inclinazione ha raggiunto il valore di 90° essa viene fatta nuovamente diminuire , passando dal valore iniziale di 80° e arrivando fino a 0°. Da 90° a 70° il valore dell'angolo misterioso va diminuendo. In corrispondenza di una inclinazione di circa 70°, l'angolo misterioso si annulla. Diminuendo l'inclinazione, per valori inferiori a 70° il punto E non si trova più sul lato obbliquo BC, ma sul suo prolungamento, e il valore dell'angolo misterioso torna ad aumentare. Giungendo ad un valore dell'inclinazione pari a 60°, l'angolo misterioso attinge un valore di 50°. Diminuendo ulteriormente l'inclinazione, per valori inferiori a 60° anche il punto D non si trova più sul lato obbliquo AB, ma sul suo prolungamento, e il valore dell'angolo misterioso continua ad aumentare. Giungendo a valori dell'inclinazione prossimi a 0°, il valore dell'angolo misterioso tende a 110°.
Naturalmente, il tutto può ricavarsi anche per via analitica, facendo lo studio della funzione che esprime come varia l'angolo misterioso al variare dell'angolo di inclinazione dei lati obliqui. Con un procedimento simile a quello seguito da Paolo per la soluzione da lui proposta, alla fine si ricava che l'angolo misterioso è dato da:
avendo indicato con l'inclinazione variabile dei lati obliqui del triangolo isoscele ABC e con DEA l'angolo acuto tra i segmenti DE ed EA.
Il grafico della suddetta funzione è il seguente:
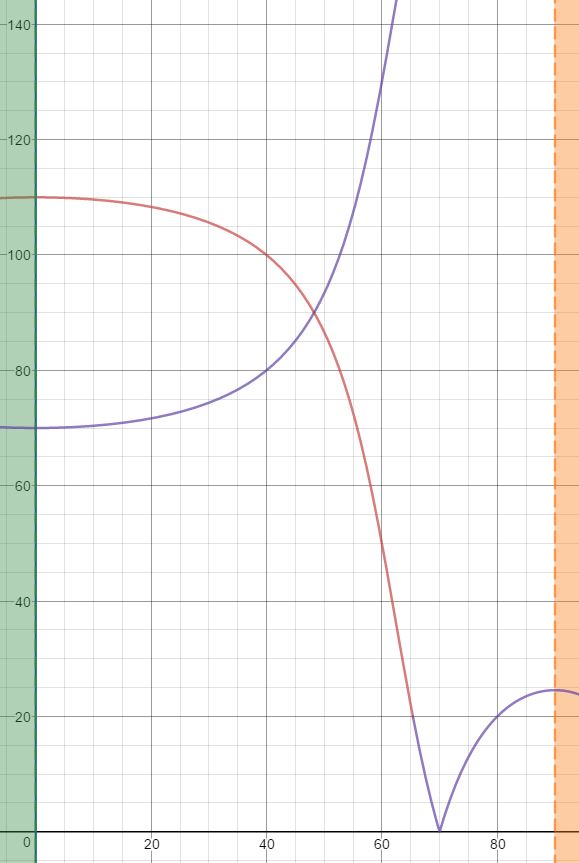
Nell'intervallo 0°-65,5° va presa in considerazione la curva marrone, mentre nell'intervallo 65,5°-90° va presa in considerazione la curva viola.
QUI trovate tutti i quiz del Club dei Maghi e QUI tutti i quiz pubblicati sul blog






3 commenti
Carissimi Maghi e Signor Paolo,
Questa notizia è arrivata come una bomba al CAC. Tutti gli archeofili e soprattutto il nostro Presidente, erano contenti come Pasque per le fantastiche soluzioni che avete trovato senza goniometro. Mi domando quali altre meraviglie avreste scoperto se solo fosse stato possibile usarlo.
Comunque, un grazie anche al Signor Gianfranco, che anche lui ha trovato, con la bellezza di 30 decimali, questi 20 gradi provvidenziali e così siamo tutti tranquilli.
Grazie a tutti anche a nome della Scienza.
Saluti estasiati
Oreste Pautasso
Complimenti per il quiz. Pur non essendo io riuscito a trovare alcuna soluzione, e' stato stimolante...
Ho trovato molto elegante il metodo geometrico per arrivare a dimostrare che ADF e' isoscele... fatto quello il quiz e' risolto...
pardon, DEF e' isoscele....