Fra i giocatori incalliti, il gioco protagonista del nostro
QUIZ è ben noto con il nome di Martingala. Vedo che tutti i partecipanti hanno capito subito perchè il gioco al raddoppio non sia conveniente.Direi che la soluzione di Fabrizio è perfetta ed è difficile scrivere qualcosa di meglio. Per cui abbiamo deciso di riportare quella. Aggiungo prima la spiegazione dei concetti che Fabrizio ha usato, ma che però potrebbero non essere noti a tutti. E' stato usato per primo il concetto di probabilità; tale concetto è talmente intuitivo che non avrebbe nemmeno bisogno di spiegazioni.
Definizione di probabilità
La probabilità che si verifichi un certo evento (un evento può essere l'uscita di un determinato numero alla roulette, oppure al lotto, ecc.) è un numero che indica appunto con che frequenza su tot ripetizioni questo può accadere; definiamo quindi probabilità p di un evento il rapporto fra i casi favorevoli e i casi possibili. In formule:
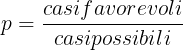
; esempi:
probabilità che esca testa o croce: 1/2; probabilità che esca il rosso: 18/37;
probabilità che esca il nero: 18/37;;
probabilità che esca il rosso o lo zero (quindi che non esca il nero): 19/37;
probabilità che esca il nero o lo zero (quindi che non esca il rosso): 19/37;
probabilità che esca un numero qualsiasi:1/37.
Somma di probabilità di eventi complementari
Un altro concetto che ha usato è il seguente; se in un gioco,in un esperimento la probabilità che si verifichi un evento è p e quella che non si verifichi è q , allora p e q e sono legate dalla formula:
p+q=1
Ciò deriva direttamente dalla definizione di probabilità; siano infatti Nf i casi favorevoli, Nnf i non favorevoli, ovvero che si verifichi il contrario; allora
p=Nf/(Nf+Nnf) ; q=Nnf/(Nf+Nnf);p+q=(Nf+Nnf)/(Nf+Nnf)=1
esempio; la probabilità che esca il rosso è 18/37; quella che non esca 19/37; la loro somma dà 37/37=1
Notiamo dal fatto che p+q=1, se la probabilità di vincere è p, la probabilità di perdere è q=1-p.
La probabilità di due eventi consecutivi
Nella dimostrazione si dicono poi due cose; si afferma che la probabilità di due eventi consecutivi (che non dipendono uno dall'altro) è data dal prodotto delle probabilità. La dimostrazione generica di questa affermazione richiede l'introduzione di concetti quali la probabilità condizionata e di eventi dipendenti e indipendenti; noi la giustificheremo con degli esempi concreti.
Supponiamo di avere delle biglie numerate da 1 a 10 in una scatola. Se estraggo un biglia a caso, la probabilità che sia la numero cinque è 1/10 ( 1 caso favorevole su 10 casi possibili.) Qual'è la probabilità che invece, rimettendo la biglia nella scatola, si estragga ancora la biglia numero 1? Tale probabilità è data da (1/10)*(1/10)=1/100, ovvero è il prodotto delle due probabilità. Perchè? Anche in questo caso dobbiamo contare i casi favorevoli. E' solo la coppia (1,1) che dà esisto favorevole. E i casi possibili? Sono tutte le coppie possibili, (1,1),(1,2), (1,3)...(1,10)...(2,1),(2,2),..(2,10).......(10,1),.(10,2),...(10,10). che sono 10 x 10=100 quindi la probabilità è sempre 1/100. Complichiamo un po' il ragionamento;Cerchiamo la probabilità che la prima biglia sia 1 e la seconda un numero pari. Siano p,q tali probabilità. Allora p=1/10, q=5/10=1/2, p*q=5/100; infatti i casi favorevoli sono (1,2),(1,4),(1,6),(1,8), (1,10) che sono 5, mentre quelli possibili sono sempre 100; dunque p*q=5/100. Dunque anche se e probabilità sono diverse, la probabilità che accadano i due eventi consecutivi è data dal prodotto delle probabilità.
Nel caso del rosso e nero,abbiamo 19/37 come probabilità che non esca il colore scelto; la probabilità che non esca due volte di fila è in tal caso
^{2})
. E che non esca tre volte? p=
^{2})
, q=
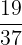
,
^{3})
,quindi quattro volte
^{4})
, cinque volte
^{5})
.
Le perdite costituiscono una successione geometrica
Altra cosa; nel caso di 5 perdite consecutive, giocando al raddoppio, la perdita è: 1+2+4+8+16=31
ma
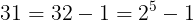
nel caso generale invece la perdita è
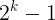
su k giocate perse. Infatti per la famosa identità:
posto a=2:
Bene, abbiamo quasi finito con i preamboli. Manca la cosa più importante, che è stata usata da Fabrizio:
Valor medio o valore atteso
Come anticipato da Quazel, per avere un indice per sapere se a lungo termine si vinca o no, ovvero si abbia un utile, bisogna introdurre il valore medio, a valore atteso.Come introduciamo tale valore? Se in un gioco si hanno due probabilità, una p di vincere e una q di perdere, e se in caso di vincita vinco x e in caso di perdita y,allora il valore atteso sarà:
Va=p*x +q*y. Perchè definirlo così? Sappiamo che vincita e perdita sono due eventi complementari, inoltre se la probabilità di vincere è minore di quella di perdere, in caso di vincita dovrei prendere più denaro, quanto basta almeno per andare a pari.Nel caso del rosso o nero il calcolo che fa Quazel è questo, indicandocon G il guadagno: G=18*1-19*1=-1<0 quindi mi aspetto un guadagno negativo giocando 37 volte;che possiamo anche riscrivere con un rapporto per calcolare un valore medio:
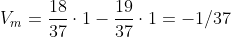
Quindi in un numero diverso di giocate, ad esempio 100, mi aspetto di perdere 100/37 di euro.
La soluzione di Fabrizio, sia nel caso k=5 che nel caso di k generico.
.....Per rispondere a questa ultima domanda utilizzerei questo schema che mi sembra possa semplificare il ragionamento.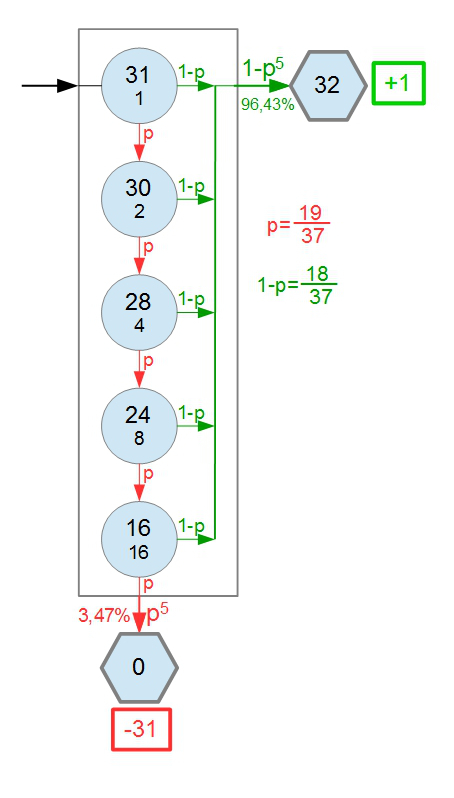
I cerchi rappresentano le giocate. I due numeri all'interno sono la somma disponibile prima della giocata e la puntata giocata. Se la giocata è positiva, allora esco dal gioco (esagono) recuperando il doppio della puntata. Se la giocata è sfavorevole, ritento (passo al cerchio sottostante) se posso raddoppiare la puntata, altrimenti esco perdendo i 31 euro.
La cosa che mi ha fatto vedere questo schema è che questo meccanismo è equivalente, dal punto di vista del risultato, ad un gioco con un unica puntata (rettangolo). La posta sono tutti i 31 euro. La vincita è la posta più 1 euro, la perdita è la posta intera. La possibilità di vincere o di perdere a questo gioco dovrebbero essere i valori vicino alle due frecce uscenti dal rettangolo.
La perdita si ha quando ci sono 5 risultati negativi consecutivi, ) . La possibilità di vincere non può che essere
. La possibilità di vincere non può che essere ) poichè è l'unica altra uscita dal rettangolo e la tornata di gioco è certo che avrà termine in una delle due uscite (o vinco o perdo).
poichè è l'unica altra uscita dal rettangolo e la tornata di gioco è certo che avrà termine in una delle due uscite (o vinco o perdo).
Il risultato medio di questo gioco partendo da 31 euro è 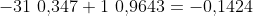 .
.
Se invece di partire da 31 ) euro si partisse da un ammontare di
euro si partisse da un ammontare di 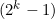 , invece di 5 giocate avrei a disposizione k giocate. Nello schema in figura cambia la lunghezza della catena delle giocate che fa cambiare le possibilità di vincita o perdita e cambia l'ammontare della perdita che è sempre il totale del capitale iniziale,
, invece di 5 giocate avrei a disposizione k giocate. Nello schema in figura cambia la lunghezza della catena delle giocate che fa cambiare le possibilità di vincita o perdita e cambia l'ammontare della perdita che è sempre il totale del capitale iniziale, 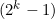 .
.
La media del risultato diventa \,&space;p^k+1\,&space;(1-p^k)=1-(2p)^k) . Nel caso di lancio della moneta, dove p=1/2 e 2p=1, la media dei risultati delle tornate è 0 indipendentemente dal capitale iniziale. Se la possibilità di perdere è maggiore di 1 volta su 2, come nel caso della roulette, al crescere del capitale iniziale la situazione lentamente peggiora. Con k=20, la media del risultato è circa -0,7.
. Nel caso di lancio della moneta, dove p=1/2 e 2p=1, la media dei risultati delle tornate è 0 indipendentemente dal capitale iniziale. Se la possibilità di perdere è maggiore di 1 volta su 2, come nel caso della roulette, al crescere del capitale iniziale la situazione lentamente peggiora. Con k=20, la media del risultato è circa -0,7.
Per giochi più rischiosi la perdita cresce molto di più rapidamente. Per un gioco con possibilità di vittoria 1 volta su 4, con k=20 la perdita media per tornata diventa più di 3000 euro contro i 6,5 euro per k=5.
Lo schema nella figura potrebbe essere lo spunto per rappresentare la modalità di gioco che riparte dal capitale accumulato. Invece dell'uscita dell'esagono in alto, ci dovrebbe essere una nuova catena. Ma la soluzione è lontana. Una cosa appare evidente. Sarà negativa in tutti i casi avendo solo uscite dal gioco con risultato negativo.
Scusate se mi sono fatto prendere la mano dal quiz molto interessante.
Conclusione
La perdita è sicura a causa di quel 1/37; giocando al raddoppio la situazione poi peggiora. Dunque l'affermazione di Quazel :
Tanto varrebbe giocarli tutti assieme sul rosso o sul nero. è giustificata. Quella piccola differenza basta per far accumulare al banco dei guadagni sicuri. Se infatti la probabilità p fosse 1/2, come nel testa o croce, se sostituiamo nella formula \,&space;p^k+1\,&space;(1-p^k)=1-(2p)^k) il valore p=1/2 otteniamo 1-1=0, cioè nessun guadagno e nessuna perdita. Pensate inoltre che le probabilità di vincita che dà il casino, che è considerato luogo di perdizione, sono ben superiori a quelle che dà lo stato in giochi come il lotto, dove paga 11 volte l'uscita di un numero che ha probabilità 1/90 di uscire. Non per niente, senza voler offendere nessuno, il politico italiano Camillo Benson definì il gioco del lotto la tassa sugli imbecilli.
il valore p=1/2 otteniamo 1-1=0, cioè nessun guadagno e nessuna perdita. Pensate inoltre che le probabilità di vincita che dà il casino, che è considerato luogo di perdizione, sono ben superiori a quelle che dà lo stato in giochi come il lotto, dove paga 11 volte l'uscita di un numero che ha probabilità 1/90 di uscire. Non per niente, senza voler offendere nessuno, il politico italiano Camillo Benson definì il gioco del lotto la tassa sugli imbecilli.
QUI tutti i quiz del club dei maghi, QUI tutti i quiz del blog

. La possibilità di vincere non può che essere
poichè è l'unica altra uscita dal rettangolo e la tornata di gioco è certo che avrà termine in una delle due uscite (o vinco o perdo).
.
euro si partisse da un ammontare di
, invece di 5 giocate avrei a disposizione k giocate. Nello schema in figura cambia la lunghezza della catena delle giocate che fa cambiare le possibilità di vincita o perdita e cambia l'ammontare della perdita che è sempre il totale del capitale iniziale,
.
. Nel caso di lancio della moneta, dove p=1/2 e 2p=1, la media dei risultati delle tornate è 0 indipendentemente dal capitale iniziale. Se la possibilità di perdere è maggiore di 1 volta su 2, come nel caso della roulette, al crescere del capitale iniziale la situazione lentamente peggiora. Con k=20, la media del risultato è circa -0,7.
il valore p=1/2 otteniamo 1-1=0, cioè nessun guadagno e nessuna perdita. Pensate inoltre che le probabilità di vincita che dà il casino, che è considerato luogo di perdizione, sono ben superiori a quelle che dà lo stato in giochi come il lotto, dove paga 11 volte l'uscita di un numero che ha probabilità 1/90 di uscire. Non per niente, senza voler offendere nessuno, il politico italiano Camillo Benson definì il gioco del lotto la tassa sugli imbecilli.






1 commento
Con le Slot Machines la tassa è diventata permanente, per gli imbecilli,ovviamente .
.