Soluzione del quiz: Un ricetrasmettitore un po' debole
Euclide o Lagrange? A voi l'ardua sentenza...
Quando si propone un quiz, assieme all'enunciato del problema, si ha in mente anche una determinata soluzione. Si sa in partenza che oltre a quel particolare modo di risolvere il problema ce ne sono altri, a volte anche molti, che potranno emergere dai vari commenti e dalla discussione.
A volte si cerca di creare qualche complicazione che renda le cose un po' più difficili. Ad esempio, in questo caso, invece di un contesto bidimensionale, avremmo potuto proporre uno scenario a tre dimensioni, dicendo semplicemente che le strade che i due ciclisti devono percorrere sono in discesa, magari adducendo, pretestuosamente, la motivazione di non farli affaticare eccessivamente. Invece abbiamo scelto di non affaticare troppo i lettori, così, con un tempo di risposta da record, è arrivata la soluzione di Mik, prima i risultati e poi la dimostrazione analitica. Ma poteva mancare il suggerimento di una scorciatoia geometrica “rocambolesca” da parte di Enzo? Certamente no! Ecco quindi che un tranquillo quiz di mezza estate offre l'opportunità di vedere, ancora una volta, confermata la regola che accanto alla via del metodo “sicuro” c'è un elegante sentiero alternativo che porta alla stessa conclusione.
Di seguito le due dimostrazioni, analitica e geometrica, tratte dai commenti pubblicati.
Soluzione di Mik
Posizioniamo i due ciclisti, diciamo X e Y, lungo gli assi di un piano cartesiano dove (inizialmente) si muovono ortogonalmente verso l'origine , che facciamo coincidere col punto P, con la medesima velocità
. Li posizioniamo lungo gli assi del piano cartesiano. L'equazione del moto dei due è:
X:
Y:
dove:
In ogni momento la distanza tra i due è:
La ricezione è massima laddove la distanza è minima. Per trovare il minimo della distanza si eguaglia a zero la derivata nel tempo, ma mi permetto una semplificazione e affermo che è minima laddove anche
è minima, e quindi posso fare meno fatica schivando le radici e trattando il quadrato della distanza:
Derivando ambo i lati rispetto al tempo:
Eguagliando a zero e svolgendo i calcoli:
il che ci dà l'istante al quale si ha la distanza minima. Sostituendo i valori si ottiene:
Dopo 6 ore i due ciclisti si trovano rispettivamente in:
X:
Y:
ovvero si trovano ai vertici opposti di un quadrato di lato 30km (cfr. disegno di Vincenzo più sopra) e pertanto distano ovviamente:
Soluzione di Enzo

Propongo un approccio puramente geometrico che sfrutti una caratteristica delle diagonali dei rettangoli aventi uguali perimetro.
Ovviamente, di tutto il percorso c’interessa solo quello che inizia con l’arrivo del ciclista A nel punto d’incrocio. Ammettiamo che sia quello che viaggia in orizzontale. In quell’istante il suo collega B deve essere a una distanza (lungo la direzione verticale) pari a 60 km (viaggiano alla stessa velocità, con una differenza di 60 km).
Facciamo procedere B verso il punto d’incrocio di una lunghezza h qualsiasi. Data la velocità uguale, nello stesso intervallo di tempo A si è spostato dello stesso valore h verso destra. Otteniamo il rettangolo B’PA’Q Che ha come lati h, 60 –h, h e 60 – h. La sua diagonale PQ non è altro che la distanza tra i due ciclisti A’ e B’. Continuando a togliere e aggiungere h ai due ciclisti, cambia il rettangolo, ma il perimetro resta uguale. E così via fino a che B arriva in P e A in A”.
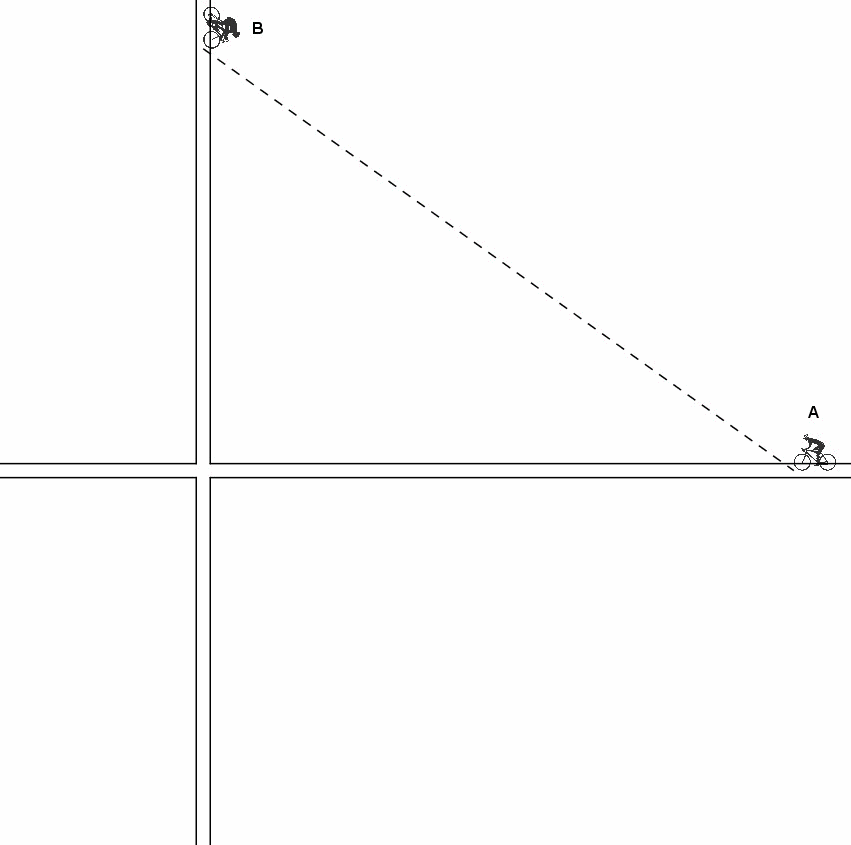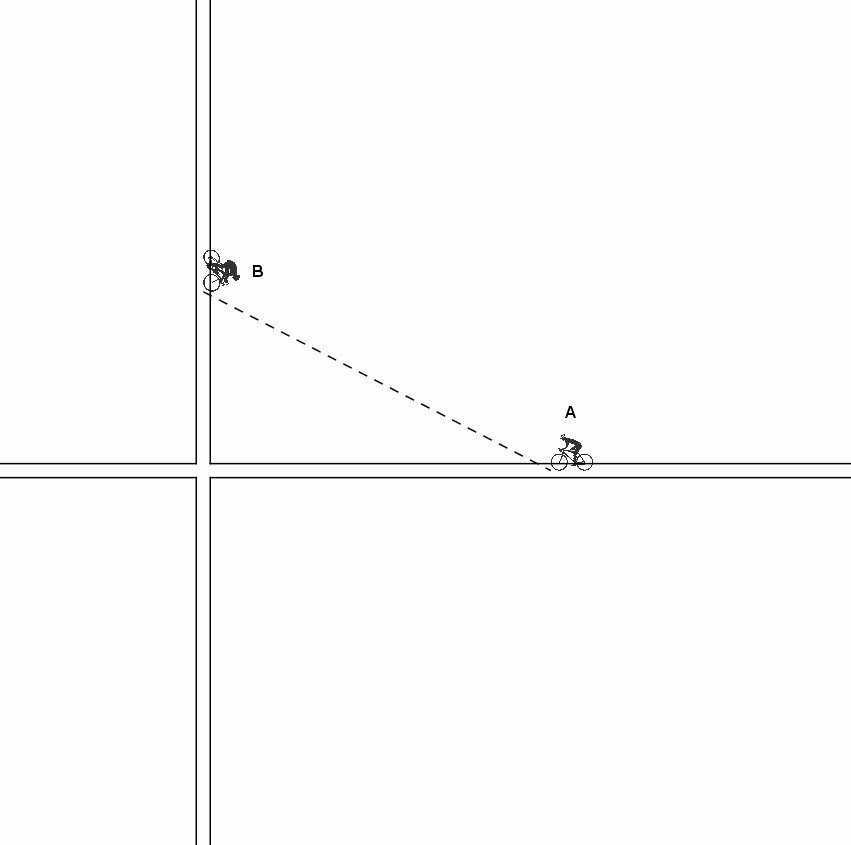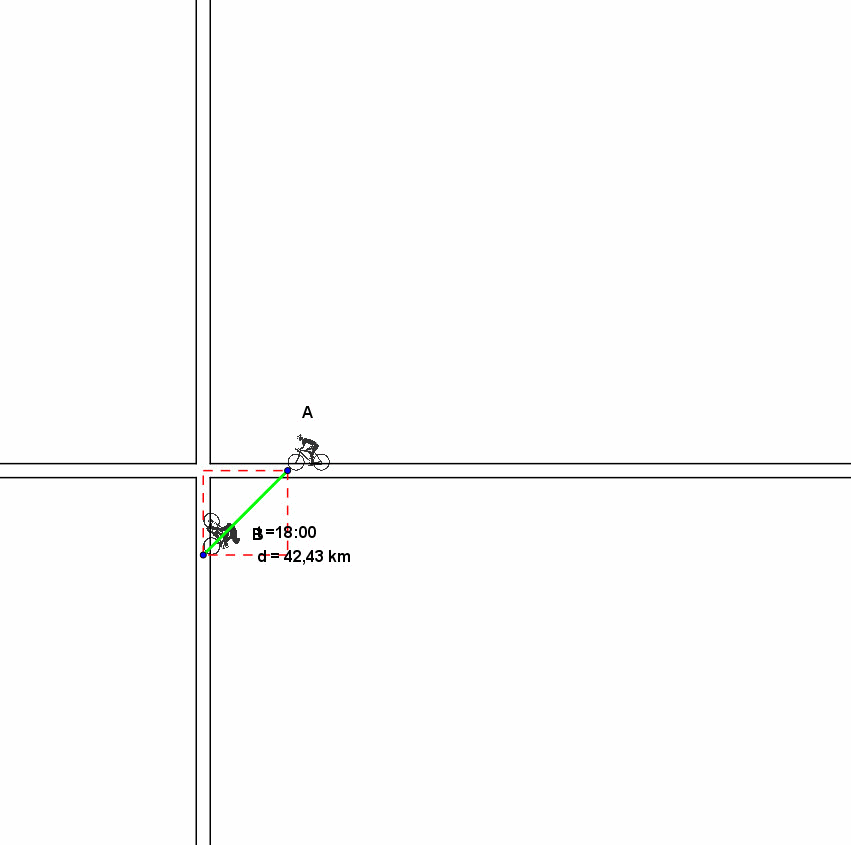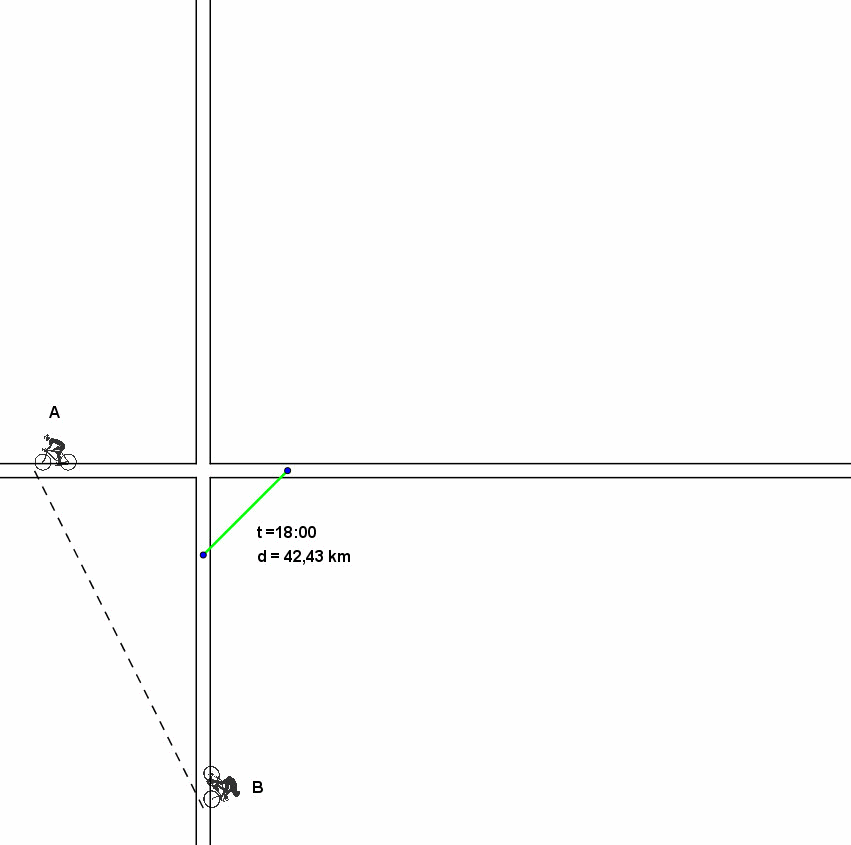
Una proprietà dei rettangoli di uguale perimetro è quella che dice che la minima diagonale si ottiene per il quadrato, ossia per una configurazione come quella disegnata in rosso. Ne segue che la minima distanza si ha a metà strada tra B e B’’ e A e A”.
Che questa sia la minima distanza si vede subito unendo gli spigoli esterni dei rettangoli: essi stanno ovviamente su una retta (per costruzione) e la minima distanza tra P e questa retta deve essere la perpendicolare, ossia PM.
Ne segue che la minima distanza si ha per 30(2)1/2.
L’ora di tale configurazione sono le 18. Infatti, A arriva in P 5 ore dopo la partenza (150/30), ossia alle 17, ma poi deve ancora percorrere la metà di 60 km, ossia 30 km che corrispondono a un’ora.
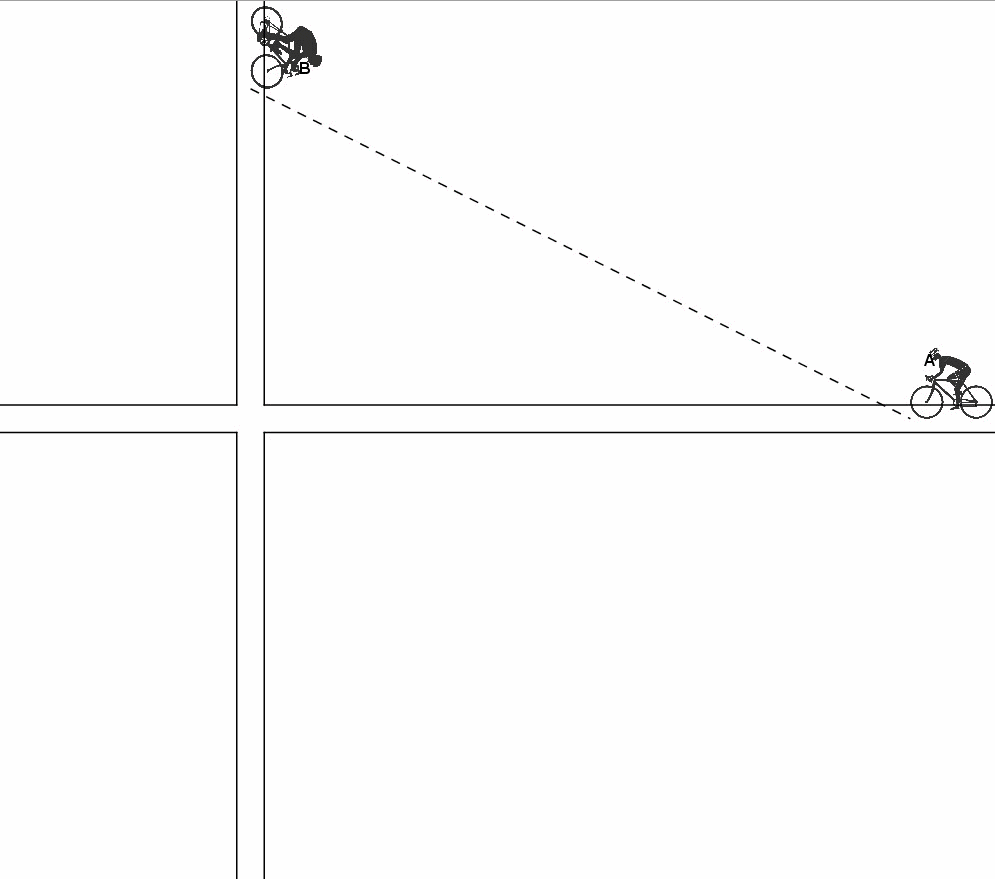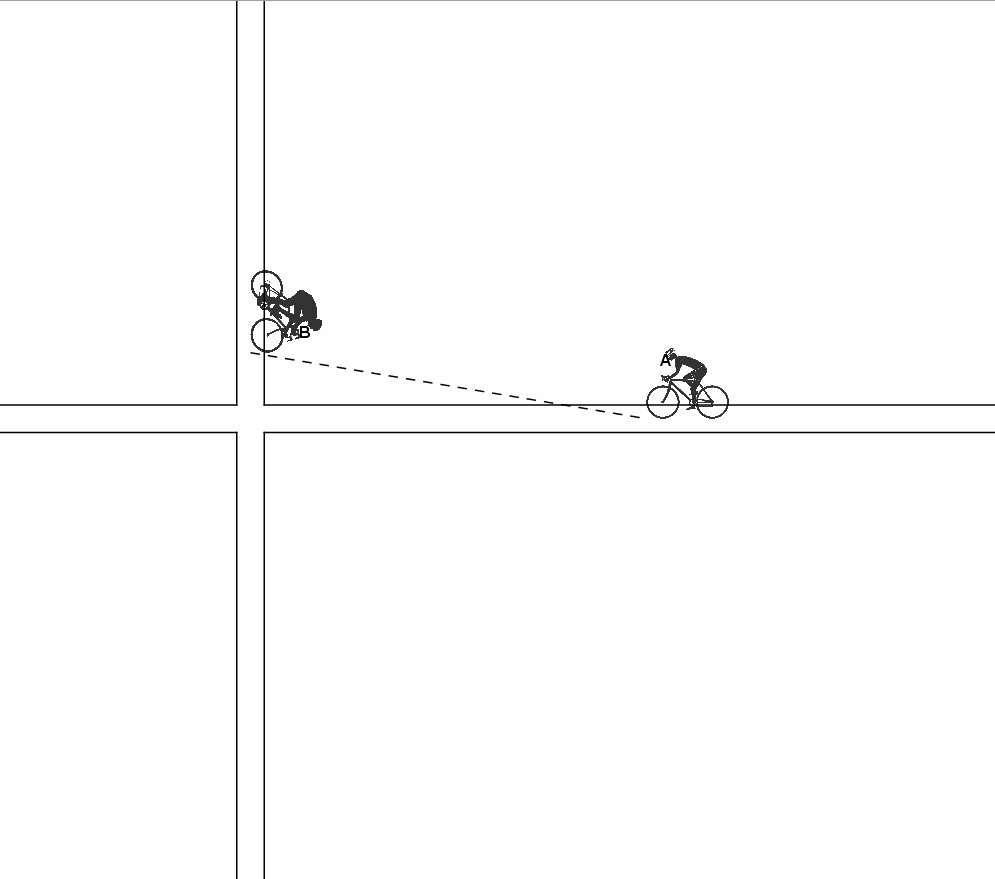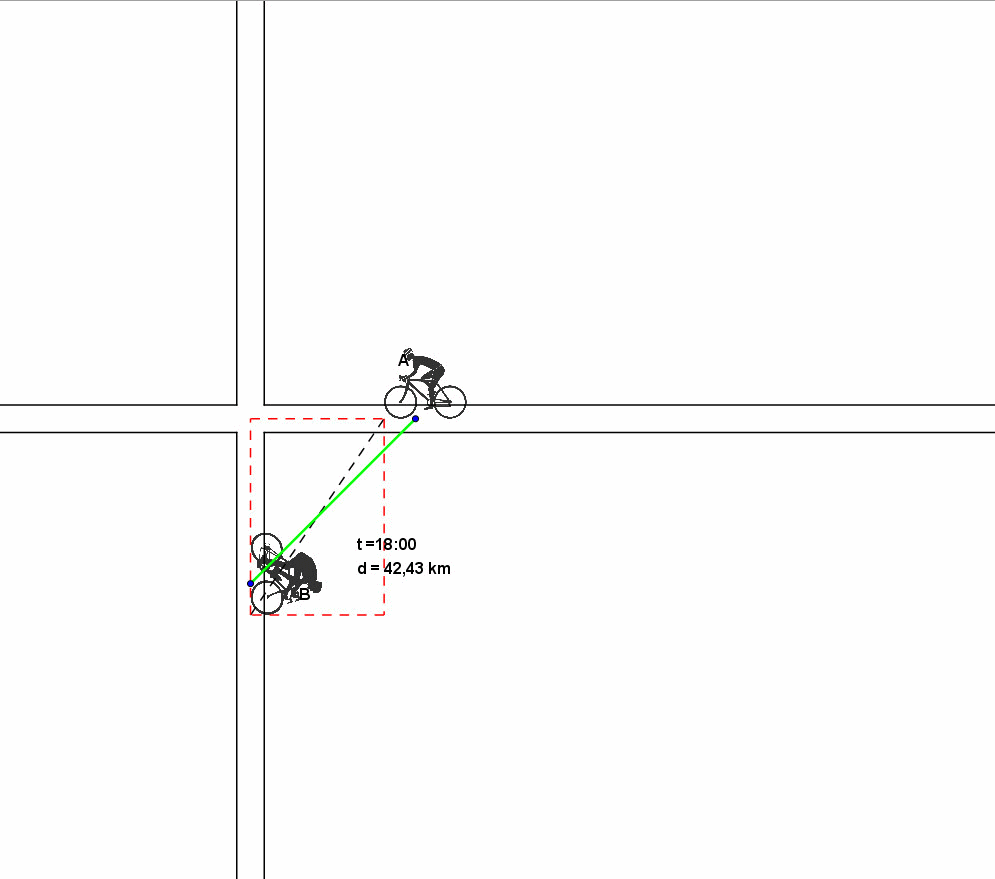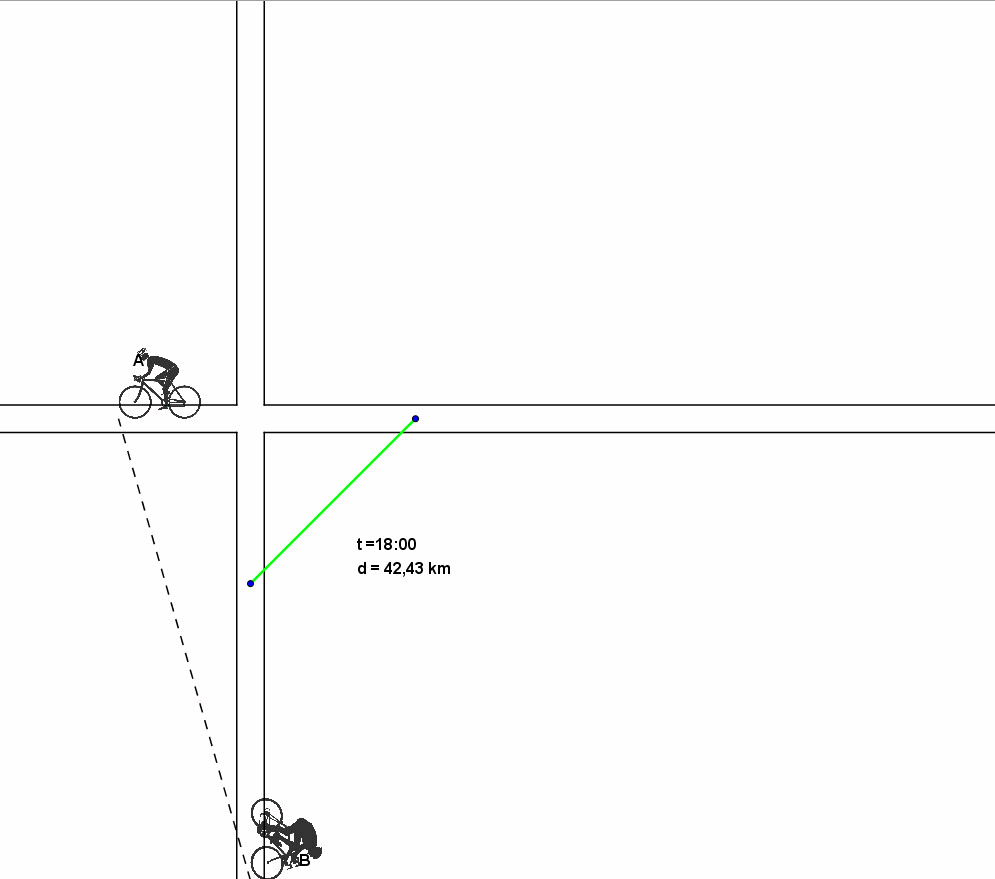
Infine vi proponiamo una animazione che illustra graficamente ciò che accade, con un successivo zoom sulla zona dell'incrocio in cui sono stati evidenziati i rettangoli di uguale perimetro della soluzione di Vincenzo.






1 commento