Mini-quiz: Polinomi e derivate.
Vorrei riprendere alcuni concetti necessari per introdurre un problema su polinomi e derivate, tanto per cambiare un po' argomento. Sono incappato in questo problema scrivendo un nuovo articolo, e volevo capire la sua difficoltà con l'aiuto di voi lettori. In pratica lo propongo come quesito.
Bene o male, i polinomi li conoscono tutti fin dalle superiori, e così pure le loro derivate. Vediamo quali altre definizioni serve sapere.
1)Ricordo che con n! si indica il prodotto dei primi n numeri interi, ovvero:
2) Ricordo anche cos'è un polinomio a coefficienti interi: non è altro che un polinomio di questo tipo
dove si suppone che tutti gli a0,a1,..an siano degli interi, ovvero appartengano a .
3) Sappiamo poi che per fare la derivata di un polinomio, basta derivare i singoli addendi, e poi sommarli; la derivata di un singolo addendo è:
Questo è tutto ciò che è necessario sapere.
Ebbene il problema che vi sottopongo è il seguente; dato un qualunque polinomio a coefficienti interi g(x), se indichiamo con la derivata di ordine h di g(x), allora sappiamo che
sarà un polinomio con certi coefficienti. Ebbene, vogliamo dimostrare che tutti questi coefficienti sono divisibili per h! (h fattoriale).
Sembra una cosa senza un senso compiuto; in realtà questo problema fa parte di una delle più importanti dimostrazioni della moderna teoria dei numeri, che affronteremo in seguito. Come di consueto, non darò la soluzione di questo mini-quiz, che sarà lasciata ai lettori con i loro commenti.
28 commenti
Un chiarimento...
Alcuni , o addirittura tutti i monomi che compongono il polinomio possono avere grado "n" inferiore all'ordine "h" della derivata. In questo caso, alla derivazione "n+1" il loro coefficiente si azzera . Lo zero non appartiene all'insieme Z. E' lecito dire che zero è divisibile per h! (?).
perché lo zero non dovrebbe appartenere a Z? Gli interi relativi vanno da meno infinito a più infinito. Comunque zero e divisibile per qualsiasi numero..diverso da zero
Procedendo con le derivazioni, per ciascun monomio del polinomio, considero l'evoluzione di questo rapporto:
numeratore = coefficiente * grado ( il grado decresce sempre di 1, a partire da n fino ad arrivare a n-h+1)
denominatore = ordine della derivazione ( l'ordine cresce sempre di 1, a partire da 1 fino ad arrivare ad h)
Inizialmente il coefficiente è "a"; eseguendo le progressive derivazioni lo moltiplico in questo modo:
prima: n/1 il numeratore è divisibile per il denominatore
seconda: n (n-1)/2 idem perché n*n-1 è sempre divisibile per 2 ( uno dei due fattori al numeratore è pari)
terza: n(n-1)(n-2) /2* 3 idem perché n*(n-1)*(n-2) è sempre divisibile per 3 ( uno dei tre fattori al numeratore lo è)
e così via.
Ad ogni passo questo rapporto resta intero perché tra i numeri che compongono il numeratore ne ho sempre uno divisibile per il numero che vado ad aggiungere al fattoriale al denominatore.
Sappiamo già che se ad un certo punto il coefficiente del monomio si azzera, perché abbiamo derivato una costante, è comunque divisibile per h!
Posso dirti che la strada giusta è proprio questa Maurizio. Altro no.
adesso che Maurizio ha spianato la strada concentriamoci sulla divisibilità di quel prodotto decrescente di interi per h!. Sono sicuro che troverete una soluzione più semplice della mia che.é come sempre un po' troppo " accademica". Le danze sono aperte a tutti..
un aiutino? pensate solo al coefficiente del termine senza x...
Nel polinomio di grado n>h supponiamo sia presente il termine a*x^h. Quando questo monomio viene derivato h volte, diventa:
(h)*(h-1)*(h-2)*....*(h-h+1) * a (ossia una costante)
Nella catena di moltiplicazioni prodotta a seguito delle successive derivazioni, che precede il coefficiente "a", si riconosce il valore di h! Quindi in questo caso è evidente la divisibilità per h!
Per i monomi di grado inferiore ad h, nel corso delle derivazioni si arriverà ad azzerare il coefficiente. Anche in questi casi si avrà la divisibilità per h! dato che zero/h! = zero
Resta da studiare il caso dei monomi che hanno esponente superiore ad h, da h+1 fino a n, estendendo le considerazioni fatte per il monomio di grado h...
Si - può - fare ! https://www.youtube.com/watch?v=Gp3gyx782eg
Mi sembra che Maurizio abbia dato già la soluzione. Forse ci sarebbe da aggiungere che è valida solo per coefficienti interi perché un razionale potrebbe elidere qualcuno dei fattori del fattoriale.
Un modo diverso per arrivare al risultato, forse meno matematico, potrebbe essere questo.
La derivata h-esima di uno dei termini del polinomio è:...(n-(h+1))x^{n-h}=a_n&space;\frac{n!}{(n-h)!}&space;x^{n-h})
Quel rapporto tra fattoriali mi ricorda i coefficienti binomiali
che corrispondono al numero delle possibili combinazioni di n oggetti presi ad h ad h senza ripetizioni.
Quindi la derivata di sopra la posso scrivere come
Ora un numero di combinazioni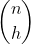
è un intero. Una combinazione c'è o non c'è. Dire 5 combinazioni e 3/4 non ha senso. Quindi un qualsiasi coefficiente del nostro polinomio derivato per h volte è il prodotto di 2 numeri interi moltiplicato per h! che evidentemente è divisibile per h!.
Posso scrivere ogni termine del polinomio nel seguente modo:
an x(n-h)xh
Poniamo tutti gli x(n-h) come se fossero costanti e i coefficienti iniziali uguali a 1 (non influisce assolutamente sul risultato).
Vanno eliminati tutti termini per cui n < h dato che derivando vanno a zero
Il che vuol dire che facendo la derivata h-esima ogni coefficiente deve essere h (h-1)(h-2)…1 ossia h!
Poi, in realtà, bisognerebbe svolgere le derivate anche della parte giudicata costante, ma il risultato è assicurato…
Buttata lì...
Vedo che siamo tutti concordi sul fatto che il problema si presenta quando si tratta di derivare monomi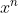
con n>h. Ho pensato su un po' anche al discorso di Vincenzo, in cui da quello che ho capito scrive 
e da qui si applica la regola di Leibniz del prodotto tenendo costante prima un termine e poi l'altro; il fatto è che n-h può essere ancora maggiore di h ma si potrebbe, essendo n>h, scrivere 
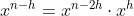; procedendo iterativamente finchè n<=h si arriva al risultato , penso che Vincenzo volesse dire questo.Non so, bisognerebbe scriverlo per bene formalmente. Ci proverò.Per quanto riguarda la soluzione di Fabrizio, è esattamente quella che avevo pensato io. Perchè dici che è meno matematica? L'unica cosa che si potrebbe sollevare, è che non tutti forse conoscono i coefficienti binomiali. Ho provato a cercarli nel sito con la funzione "cerca", ma non sono riuscito a trovarli. Penso però che se ci sono, Daniela saprà indicarci dove. Resta comunque il dubbio se sia possibile dimostrare il fatto che \cdot&space;....(n-h+1))
sia divisibile per h! , direttamente (senza passare per i coefficienti binomiali). Comunque se qualcuno vuole provarci è ancora in tempo.
Proviamo in questo modo ...
Il polinomio di grado "n" è costituito da monomi di grado variabile da 0 a "n", tutti con coefficienti interi, per ipotesi.
Eseguendo le h derivazioni, ad ogni derivazione i coefficienti vengono moltiplicati per un numero intero (l'esponente di x). Quindi il coefficiente di x^n è moltiplicato complessivamente (h volte) per
n*(n-1)*... *( n-h+1 )
Ad esempio: a*x^5 ( n= 5 ) , derivato 3 volte (h=3) risulta... a* 5*4*3 * x^2
Si tratta quidi di un numero intero, che posso anche scrivere in questo modo:
n*n-1*...*n-h+1 che è equivalente a...
= n!/ (n-h)! e mettendo in evidenza h! ...
= h!*(h+1)*...*(h+(n-h))/ (n-h)!
Da cui si deduce che si tratta di un numero multiplo di h!
applicando quanto detto al precedente esempio, considero il moltiplicatore del coefficiente "a", che è:
5*4*3
= 5!/(5-3)!
= 3!*(3+1)*(3+2)/2! divisibile per 3!
scusa Maurizio non riesco a capire questo passaggio
n*n-1*...*n-h+1 che è equivalente a...
= n!/ (n-h)! e mettendo in evidenza h! ...
= h!*(h+1)*...*(h+(n-h))/ (n-h)!
anche perchè ci vedo poco; riusciresti a scriverlo con latex?
Il coefficiente binomiale è servito
http://www.infinitoteatrodelcosmo.it/2015/11/13/39-bis-soluzione-degli-esercizi-sulle-serie-di-mclaurin/
grazie mille.
Umberto,
la soluzione che ho proposto mi sembra "meno matematica" perché fa uso della affermazione che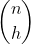
è un numero intero. La dimostrazione formale di questa affermazione credo che ci riporterebbe al punto di partenza. Per rompere questo ragionamento circolare ho introdotto ciò che rappresenta il coefficiente binomiale, cioè il numero di combinazioni, dicendo che sono intere. Però, per come l'ho giustificata, l'affermazione che il numero di combinazioni è un intero mi suona quasi un fatto "sperimentale" più che dimostrato.
capisco i tuoi dubbi che sono stati anche i miei.Dicevo solo che il calcolo combinatorio fa parte bene o male della matematica. Il fatto è che non ne abbiamo mai parlato a fondo. Cercherò di dire qualcosa a riguardo.Ma per me non è un fatto sperimentale. Le disposizioni si ricavano dalle combinazioni moltiplicando per K! Questa per me è matematica.
Aggiungo al mio commento precedente...
Nella espressione del coefficiente che si ottiene dopo le h derivazioni..
....(h+(n-h))}{(n-h)!})
il numeratore contiene h!
Eseguita la divisione per h! ci resta questo rapporto...
Per convincersi che esso rappresenta un numero intero, si può pensare al fatto che sia la produttoria al
numeratore, sia quella al denominatore, sono costituite da un ugual numero di fattori (n-h) in sequenza.
se n-h = 4 avremo
numeratore (h+1)*(h+2)*(h+3)*(h+4)
denominatore 1* 2* 3* 4
h+1 è sempre divisibile per 1.
h+2 o il numero precedente è divisibile per 2
h+3 o uno dei due numeri precedenti è divisibile per 3
h+4 o uno dei tre numeri precedenti sarà divisibile per 4
Questa situazione si ripropone per qualsiasi valore di h, dipende dalla struttura del rapporto.
Ok, chiudiamo pure qui e diamo spazio ad Achille; mi riserverò di dare delle precisazioni sulla soluzione, almeno per quanto riguarda l'uso dei coefficienti binomiali, che forse può lasciare delle perplessità.
Scusa Umberto, invio questo ulteriore tentativo di risposta che avevo quasi completato prima del tuo ultimo messaggio.
Pensandoci ancora sopra mi sono convinto sempre di più che il modo indicato da Maurizio possa portare ad una dimostrazione della presenza di h! nei coefficienti della derivata h-esima del polinomio.
Credo però che ci sia un punto da chiarire nel ragionamento. Forse una pignoleria, ma puntando ad una dimostrazione occorre affrontarla.
Riassumo la situazione prima di passare al punto da chiarire.
Ragioniamo sul termine
del polinomio. Possiamo ragionare mettendo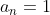 
, posto che sia un intero il suo valore non ha effetti sul ragionamento. Il coefficiente della derivata h-esima di questo termine è una sequenza di numeri interi consecutivi che va da (n-h+1) a n. Il nostro obiettivo è quello di dimostrare che questa sequenza è divisibile per h!, qualsiasi siano n ed h.
Ora vengo al punto che ritengo sia da chiarire.
Quando si dice che il prodotto di una sequenza di h numeri interi consecutivi è divisibile per ciascuno dei fattori di h! si dice una cosa vera. Questo però non garantisce che sia divisibile per tutti i fattori di h! insieme. Faccio un esempio banale con un solo numero. Nella sequenza ci potrebbe essere un numero dato dal prodotto di 4 per un numero primo (es.44 o 428). Questo numero è divisibile per 2 e 4, ma non per 2x4. Evidentemente non siamo in questo caso super semplificato, ma nulla ci garantisce che non ci sia un problema di questo tipo, a meno di non dimostrare il contrario.
Per fare questa dimostrazione credo che occorra non solo dire che c'è almeno un numero divisibile per ciascuno dei fattori di h!, ma dire anche quanti sono. Ci possiamo limitare anche ai numeri primi che compongono tutti gli altri.
Confrontiamo quanti sono in h! e in una sequenza qualsiasi di h interi consecutivi come quelle che troviamo nei coefficienti delle derivate del polinomio.
Partiamo da h!.
Prendo come esempio i multipli di 3.
Di numeri divisibile per 3 ce ne sono h/3. Però questa frazione può essere non intera. Quindi devo dire che è l'intero uguale o minore di h/3. Cioè h/3 arrotondato all’intero per difetto. Lo scrivo come intinf(h/3).
Ma non basta perché di 3 ce ne possono essere altri in 9, ancora di più in 27 ecc. Devo prenderli in considerazione almeno fino a quando il divisore è minore di h.
Anche per questi vale la stessa regola. Di multipli di questi numeri ce ne sono intinf(h/9), intinf(h/27) ecc.
Ora dobbiamo confrontare questo risultato con il numero di multipli che si trovano in una sequenza di h numeri interi consecutivi. Qui è più complicato perché dipende anche da dove inizia oltre che da quanto è lunga la sequenza.
Per avere una dimostrazione generale occorre mettersi nel caso per noi peggiore, cioè dove ce ne sono di meno. Questo è il caso peggiore perché se sono troppo pochi potremmo trovarci a non averne abbastanza per formare h!.
Per i multipli di 3 le sequenze peggiori credo siano quelle con in coda (3-1) numeri prima di un multiplo di 3 ed in testa altri (3-1) dopo un multiplo di 3 (es. 16 17 18 19 20 21 22 23). In queste sequenze il numero di multipli di 3 è dato da (h-(2 3-1))/3+1=intinf(h/3)-1+1=intinf(h/3).
Quindi anche nel caso più sfavorevole il numero di multipli di 3 nella sequenza di h interi è uguale a quello in h!. Non basta questo per esaurire il discorso sul 3. Occorre considerare anche i multipli di 9, 27 ecc. fino a che questi sono minori di h. Questi multipli aggiungono altri 3 a quelli già considerati. Il ragionamento fatto sopra per il 3 vale per qualsiasi altro numero che sostituisca il 3. Quindi anche per 9, 27 ecc. Anche di questi multipli ce ne sono in una sequenza di h interi consecutivi almeno quanti ce ne sono in h!.
Il ragionamento fatto per il 3 vale ugualmente per qualsiasi altro numero. Limitandoci ai numeri primi possiamo dire che in ciascuno dei coefficienti della derivata h-esima del polinomio ce ne sono almeno quanti ce ne sono in h!.
Questo significa che ciascuno coefficiente è divisibile per h!.
Credo che questo ragionamento, se corretto, ci avvicini alla dimostrazione che stiamo cercando.
avevo considerato queste ipotesi Fabrizio ma il tutto diventa troppo macchinoso. Capisco che è vero, ma in ogni caso preferisco la tua prima dimostrazione .Comunque il tutto chiaramente resterà scritto nei commenti, starà al lettore leggere la soluzione che preferisce. Io farò solo quella precisazione che ritengo necessaria.In fin dei conti lo scopo di questi miniquiz ê proprio questo
Il problema sollevato da Fabrizio non è affatto una pignoleria, è inevitabile e doveroso cercare chiarirlo a fondo. Aggiungo quindi qualche dettaglio, non citato in precedenza che mi ha portato alla conclusione esposta.
Analizzo il risultato della divisione del coefficiente dopo le derivazioni. Si presenta, come detto, in forma di un rapporto strutturato come una sequenza di N prodotti al numeratore (a partire da h+1) e di una sequenza di N prodotti al denominatore (a partire da 1).
numeratore (h+1)(h+2)(h+3)....
denominatore 1* 2* 3 .....
Dobbiamo dimostrare che questo rapporto è un numero intero.
A ciascun termine del numeratore associamo il corrispondente termine al denominatore, scrivendo il rapporto come prodotto di rapporti.
(h+1)/1 * ( h+2)/2 * (h+3)/3 ....
ora analizziamo progressivamente i risultati , aggiungendo ad uno ad uno i moltiplicandi.
(h+1)/1 è certamente intero. Eseguo la divisione e sostituisco (h+1)/1 con il risultato (h+1).
(h+1)*(h+2)/2 il rapporto (h+2)/2 può non essere intero se (h+2) è dispari, ma allora (h+1), ossia un "valore precedente" sarà pari, quindi posso dire (h+1)*(h+2)/2 intero.
Ora, se h+1 era divisibile per 3 , lo sarà anche (h+1)/2 , analogamente posso dire per (h+2)/2, infine, se nessuno di essi è divisibile per 3 allora lo sarà di certo (h+3)/3
Quindi, aggiungendo il terzo rapporto alla nostra costruzione...
(h+1)*(h+2)/2 * (h+3)/3 è certamente intero perché uno dei tre termini tra parentesi è multiplo di 3.
Questo ragionamento si può estendere indefinitamente scegliendo qualsiasi valore per h , inoltre si può estendere anche scegliendo qualsiasi valore per n e conseguentemente per n-h il che determina invece di raggruppamenti di 3 rapporti, raggruppamenti di 4 , 5 etc.
Sui numeri primi avevo fatto anche io un certo ragionamento, analizzando alcune sequenze in cui apparivano, ravvicinate, coppie di numeri primi gemelli. Ad esempio questo gruppo:
101 102 103 104 105 106 107 108 109 ( i numeri primi sono: 101 103 107 109)
Ci sono 4 primi in una sequenza di 9 numeri.
Evidenziando la catena dei rapporti da moltiplicare, abbiamo:
101/1 * 102/2 * 103/3 * 104/4 * 105/5 * 106/6 * 107/7 * 108/8 * 109/9
In ciascuna riga che segue, appare la progressione dei risultati,
IMPORTANTE: ogni passaggio utilizza solo uno o più termini precedenti e/o quello in aggiunta
Progressione risultati
101/1 101
101* 102/2 101*51
101*51* 103/3 101*17*103
101*17*103* 104/4 101*17*103*26
101*17*103*26* 105/5 101*17*103*26*21
101*17*103*26*21* 106/6 101*17*103*26*7*53
101*17*103*26*7*53* 107/7 101*17*103*26*1*53*107
101*17*103*26*1*53*107* 108/8 101*17*103*13*1*53*107*27
101*17*103*13*1*53*107*27* 109/9 101*17*103*13*1*53*107*3*109
Come c'era da aspettarsi, il risultato tende ad essere un prodotto di numeri primi ( i sei numeri non primi che avevamo al numeratore - 102 104 105 106 108 - sono stati rimpiazzati, nel risultato, da altrettanti numeri primi - 17 13 1 53 3 ) ma, aggiungendo nuovi elementi a numeratore e denominatore il rapporto resta comunque intero per il modo in cui sono correlate le due catene al numeratore e al denominatore. Ogni nuovo passo trova una divisibilità nel risultato acquisito precedentemente, il denominatore scompone il numeratore in numeri primi.
Insomma, l'esempio numerico non ha assolutamente alcun valore, come dimostrazione, ma mette in evidenza un preciso meccanismo "interno" che sarebbe auspicabile riuscire a descrivere in modo più formale.
ok se volete lasciamo aperto il quiz ancora un po', visto l interesse dimostrato. Chissà che qualcuno abbia qualche idea a riguardo
Approfittando della pazienza di Umberto e di Fabrizio, provo a giustificare il motivo per cui un rapporto di questo tipo:
(h+1)*(h+2)*(h+3)*(h+4)*...(h+ x )
__________________________________
1 * 2 * 3 * 4 * 5 * ... x
ha sempre come risultato un numero intero.
Per indicare le sequenze dei numeri che vanno moltiplicati, userò la parola "stringa" ( non illudetevi che si parli di teoria delle stringhe...
)
La stringhe minime su cui ha senso ragionare sono di due elementi: 1 e 2 le scrivo inizialmente identiche, al numeratore e al denominatore. In questa situazione sono "in fase", riferendomi al rapporto più sopra ho imposto h = 0.
1 2
1 2 il rapporto vale 1
il rapporto tra i due prodotti vale evidentemente 1. Ma se ora elimino il primo valore (1) al numeratore e introduco il valore successivo a 2 (ossia 3) non faccio altro che moltiplicare il numeratore per un "nuovo numero primo" che non compare ancora al denominatore per il momento. Lo sfasamento delle stringhe, ossia h, vale ora 1
2 3
1 2 il rapporto vale 3
il rapporto, rispetto a quello precedente, viene a crescere di 3/1 (infatti ho aggiunto 3 e ho tolto 1).
Diventa pertanto un numero intero che vale il triplo di prima. Ora sfaserò ulteriormente le stringhe, nello stesso modo di prima, eliminando il 2 e introducendo il 4
3 4
1 2 il rapporto vale 6
E' stato iniettato un 2 in più rispetto a prima. Per ora non serve, ma va ad aumentare la divisibilità potenziale del numeratore. intanto il rapporto è salito di 4/2, cioè si è raddoppiato, restando sempre intero. Proseguo con lo sfasamento
4 5
1 2 il rapporto vale 10
Il rapporto viene moltiplicato per 4 e diviso per 3 . Dato che il numeratore conteneva il 3, entrato due passaggi prima di questo, il risultato rimane intero.
Da notare che ora al numeratore è comparso il 5 che tra due passaggi dovrà uscire, così come era prima entrato ed ora è uscito il 3.
Passiamo ora a vedere cosa succede con una struttura più articolata, formata da stringhe di 5 elementi...
Considero questa struttura di due stringhe di numeri strettamente crescenti e inizialmente identici. Lo "sfasamento" tra le stringhe (h) vale zero
1 2 3 4 5 prodotto = 120
1 2 3 4 5 prodotto = 120 rapporto dei prodotti = 1
Ora opero sulla stringa superiore, del numeratore, eliminando il numero minore e accodando al maggiore il suo successivo. Come dire che ora lo sfasamento h vale 1
2 3 4 5 6 prodotto = 120 *6/1
1 2 3 4 5 prodotto = 120 rapporto dei prodotti = 6
ripeto lo stesso schema per h=2
3 4 5 6 7 prodotto = 120 *6/1 *7/2
1 2 3 4 5 prodotto = 120 rapporto dei prodotti = 21
ripeto lo stesso schema per h=3
4 5 6 7 8 prodotto = 120 *6/1 *7/2 *8/3
1 2 3 4 5 prodotto = 120 rapporto dei prodotti = 56
Il motivo per cui il rapporto dei prodotti resta intero sta nel fatto che a partire dal primo risultato (che vale 1, con le stringhe in fase) il numeratore viene moltiplicato per un numero intero via via crescente ed sempre multiplo del nuovo divisore ( i divisori seguono l'ordine dei numeri naturali).
Il punto nodale è che i numeri primi ( ma anche gli altri che serviranno a mantenere intero il rapporto) entrano al numeratore sempre in "anticipo" rispetto a quando appariranno al denominatore.
Ad esempio, ad un certo punto moltiplicherò quella sequenza per 17/12 e, cinque passaggi dopo, la moltiplicherò per 22/17. E' evidente che in quel momento troverò un numeratore che già contiene il numero 17 per il quale devo eseguire la divisione.
Via via che le due stringhe si allontanano (al crescere di h) aumenta solo il risultato del rapporto, che resta comunque intero.
Anche la lunghezza delle stringhe non ha influenza se non sul valore del risultato. Inizialmente, quando le due stringhe sono in fase e h vale 0, il risultato è sempre = 1 , poi al progredire dello sfasamento il risultato del rapporto cresce restando intero, a valori tanto più grandi quanto più lunghe e quanto più sfasate sono le stringhe.
Anche questo ragionamento meriterebbe una esposizione meno ingenua e più matematica.
Proseguendo il precedente commento... intendo mostrare il meccanismo con cui, aumentando h, il rapporto dei prodotti dei 5 numeri al numeratore e dei 5 al denominatore permane sempre intero
A fianco della prima colonna che indica il valore di h , abbiamo nella seconda colonna i numeri primi per cui viene moltiplicato il coefficiente e nella terza quelli per cui viene diviso.
Nei primi 5 passi "escono" i numeri che formavano il quintetto iniziale al numeratore (questo fa si che il rapporto resti intero) contemporaneamente, passo passo entrano i numeri primi contenuti nei numeratori delle frazioni per cui vado moltiplicando il coefficiente iniziale. Ciascuno di questi valori staziona nel numeratore per 5 passaggi, finché viene espulso (quando si ritrova nel denominatore della frazione per cui moltiplico).
Questa situazione garantisce che in ciascun momento il numeratore conterrà i numeri primi in valore e quantità necessari a mantenere intero il rapporto.
I valori di n e di h non influenzano in alcun modo questa dinamica.
Riprendo ad inserire qui i commenti.
Volevo chiedere un chiarimento a Maurizio riguardo la
Non riesco a identificare a quale variazione si riferisce la moltiplicazione di r per (M+1)/m.
Se la penso come incremento di n dovrei moltiplicarlo per (n+1)/(n+1-h)=(M+1)/(M-m+2).
Nel numeratore di r M=n e m=h+1
Nel commento sopra non è apparso il link che avevo messo verso il post di Maurizio.
Lo metto qui come testo.
http://www.infinitoteatrodelcosmo.it/2018/05/11/precisazioni-sulla-soluzione-del-quiz-polinomi-derivate/#comment-284237
Stiamo parlando di questo rapporto
come detto ( al link citato da Fabrizio) occorre dimostrare che rappresenta sempre un numero intero.
Detto a parole: il prodotto di k numeri in sequenza , diviso per il fattoriale di k è un intero.
esempio 1*2*3*4*5 / 5! è intero. Questo è il caso più ovvio, numeratore e denominatore sono identici e il rapporto vale 1.
Ma se considero 4*5*6*7*8 / 5! come posso dire con certezza che è un numero intero? Ebbene basta iniziare con il caso banale ed osservare come da esso si può arrivare ad un qualsiasi altro caso.
Dalla sequenza 1*2*3*4*5 faccio uscire 1 e faccio entrare 6, ossia moltiplico per il massimo +1 , ( 5+1) e divido per il minimo (1), Ottengo 2*3*4*5*6 al numeratore. Il rapporto con 5! resta intero (ho moltiplicato per un intero)
Ripeto l'operazione di moltiplicare il risultato per la frazione (M+1)/m e ottengo.
2*3*4*5*6 * (7/2) = 3*4*5*6*7*8 al numeratore , proprio la sequenza su cui ci siamo interrogati. Questa volta non ho moltiplicato per un intero (7/2 = 3,5) tuttavia il denominatore di 7/2 è contenuto nel numeratore, e non per caso, dato che il denominatore (m) è proprio il valore ricavato dal numeratore, il suo termine più piccolo.
Potremmo dire che nella frazione (M+1)/m.... "il moltiplicatore di oggi è il divisore di domani" dato che dopo 5 passaggi il valore massimo scivola all'ultimo posto, diventando valore minimo.
La ripetitività di questa operazione ci consente di dire che la sequenza del numeratore di r è sempre divisibile per la sequenza al denominatore, dando quindi regolarmente un numero intero.
Riprendendo la domanda di Fabrizio...
Se penso ad un monomio di grado n, derivato h volte, il suo coefficiente sarà collegato a questo r. Un monomio di grado n+1, sempre derivato h volte , sarà collegato ad un "altro r" , ( chiamiamolo r' ) che come dice Fabrizio, deve valere r' = r * (n+1)/(n+1-h)= r* (M+1)/(M-m+2). Ma questo nuovo r' avrà anche esso una struttura simile ad r. Se prima avevo il prodotto di 5 numeri in sequenza diviso 5 fattoriale, ora avrò 6 numeri in sequenza diviso 6 fattoriale. E torniamo al discorso di dover dimostrare che anche questo r' è un numero intero.
In conclusione: il senso di moltiplicare r per M+1 /m non è legato ad una variazione di n ma è funzionale a dimostrare che un rapporto del tipo 101*102*103*104 /4! è di certo un numero intero.
Per inciso 101*102*103*104/4! rappresenta il valore di r per un monomio di grado 104, derivato 100 volte,