Categorie: Matematica Quiz
Tags: esagono geometria proiettiva Pappo Pascal prospettiva quiz soluzione teorema di Pappo
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione dell’esagono pazzo e il via alla geometria proiettiva **
Riportiamo la soluzione del quiz sul poligono pazzo, già largamente compresa da alcuni lettori, e spieghiamo perché solo uno dei tre amici è riuscito a risolverlo. Non poteva che essere Pappo, dato che tutto si collega al "suo" teorema… Il quiz è solo un inizio che ci porterà verso la geometria proiettiva e la sua fondamentale importanza nella storia dell’arte.
Questo quiz, brillantemente risolto, assume particolare importanza per due motivi. Il primo si riferisce alla sua origine che si deve a Pappo di Alessandria, matematico del tardo ellenismo, capace di dare un ultimo colpo di coda alla geometria classica che si era ormai spenta lentamente.
Il secondo perché pone la basi ancora primitive per la geometria proiettiva, ossia quella che permette di descrivere rigorosamente le leggi della prospettiva, introducendo i punti all’infinito nello spazio euclideo. In realtà, il quiz si riferisce alla versione molto più recente di Pascal, che generalizza il teorema di Pappo alle coniche.
Il teorema dell’esagono di Pappo dice (occhio che se ne danno molto versioni) che se in un esagono ABCDEF i punti dispari (A,C,E) stanno su una retta e quelli pari (B,D,F) su un’altra retta complanare alla prima, allora i punti X,Y e Z di incontro di lati opposti dell’esagono sono anch’essiallineati. La Fig. 1 illustra la situazione:
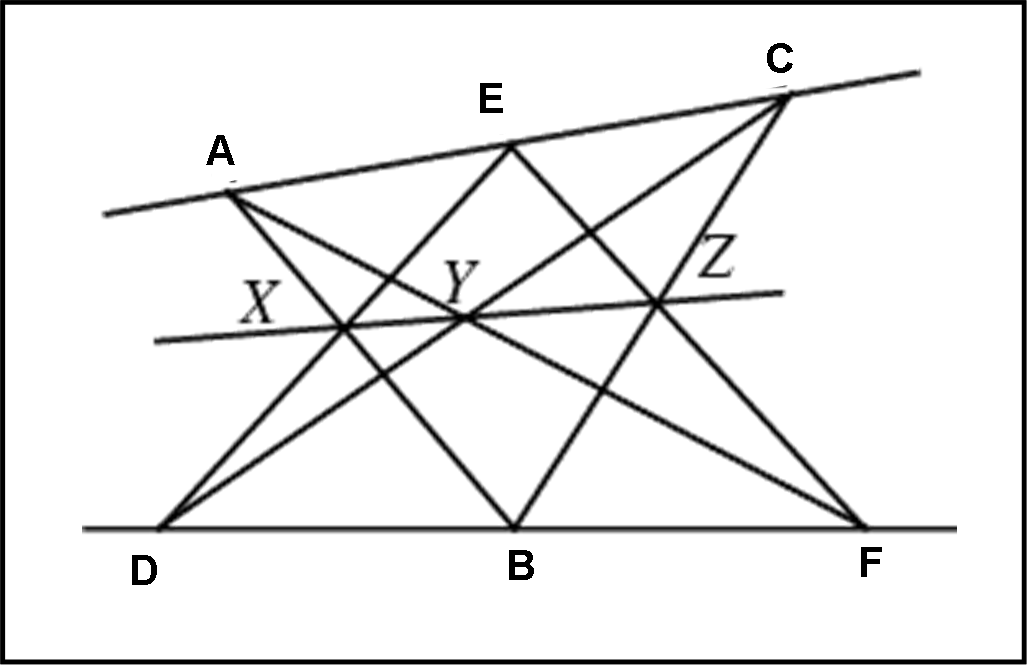
Possiamo semplificare l’enunciato, prendendo tre punti A,B e C su una retta e altri tre A’, B’ e C’ su un’altra retta. Unendo A con B’ e B con A’, A con C’ e C con A’ e, infine, B con C’ e C con B’, otteniamo tre punti X,Y e Z che sono allineati (Fig. 2). Questo è l’approccio che seguiamo.
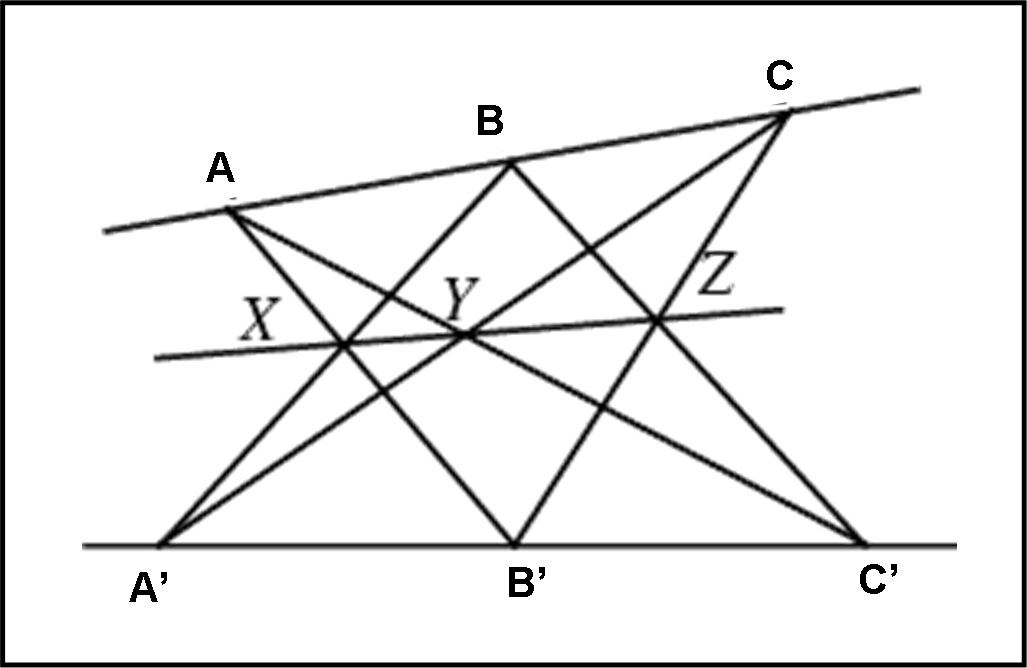
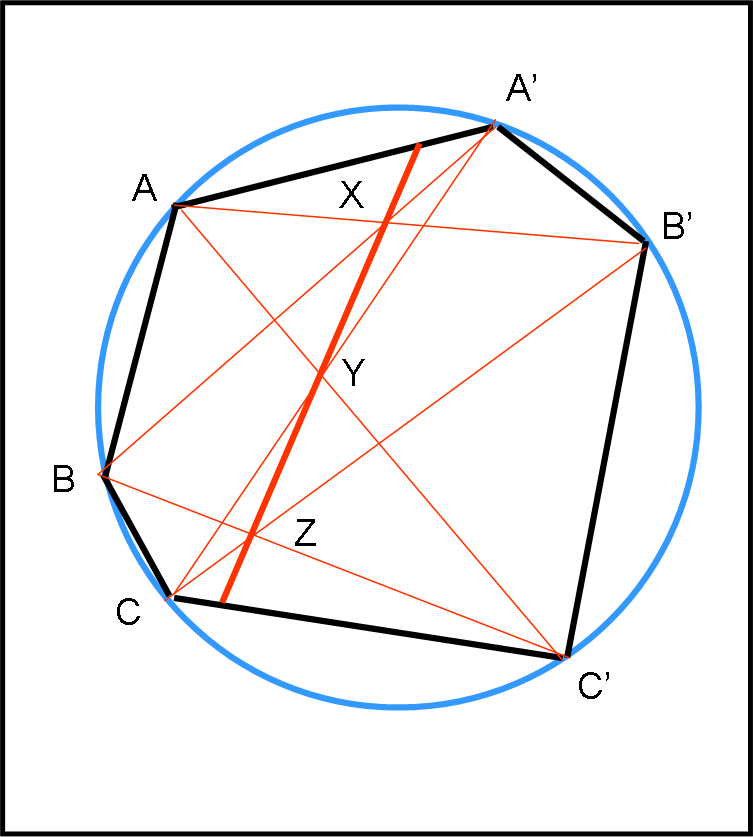
Il teorema di Pascal generalizza il teorema di Pappo e considera i sei punti su qualsiasi conica (Fig. 3) trovando che le intersezioni stanno su una retta; proprio il caso delle figure del nostro quiz, dove la conica scelta è il cerchio.
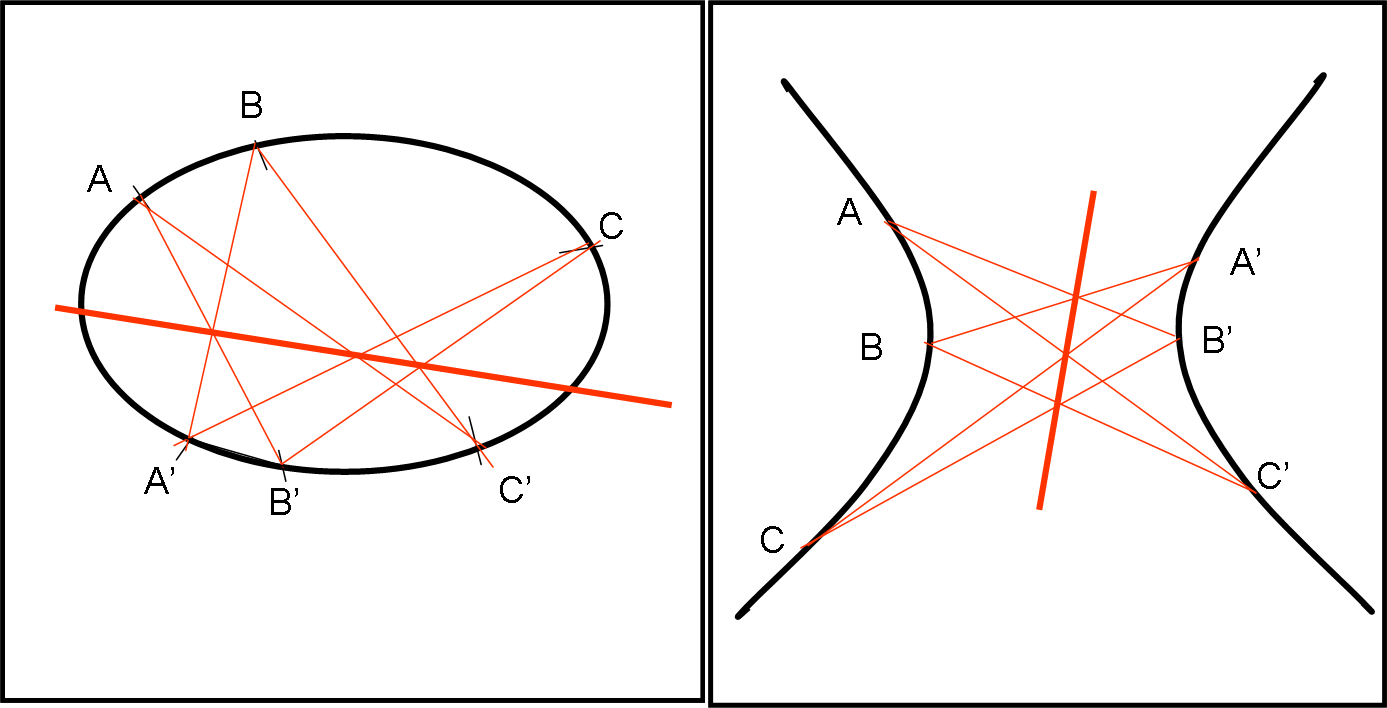
A seconda di come si applichino i teoremi e dell’esagono considerato, si possono cominciare a notare i legami con la prospettiva, ovvero con la geometria proiettiva. Ma su questo torneremo tra breve… Cosa c’è di più bello che legare regole geometriche alla realizzazione di opere d’arte ancora insuperate?
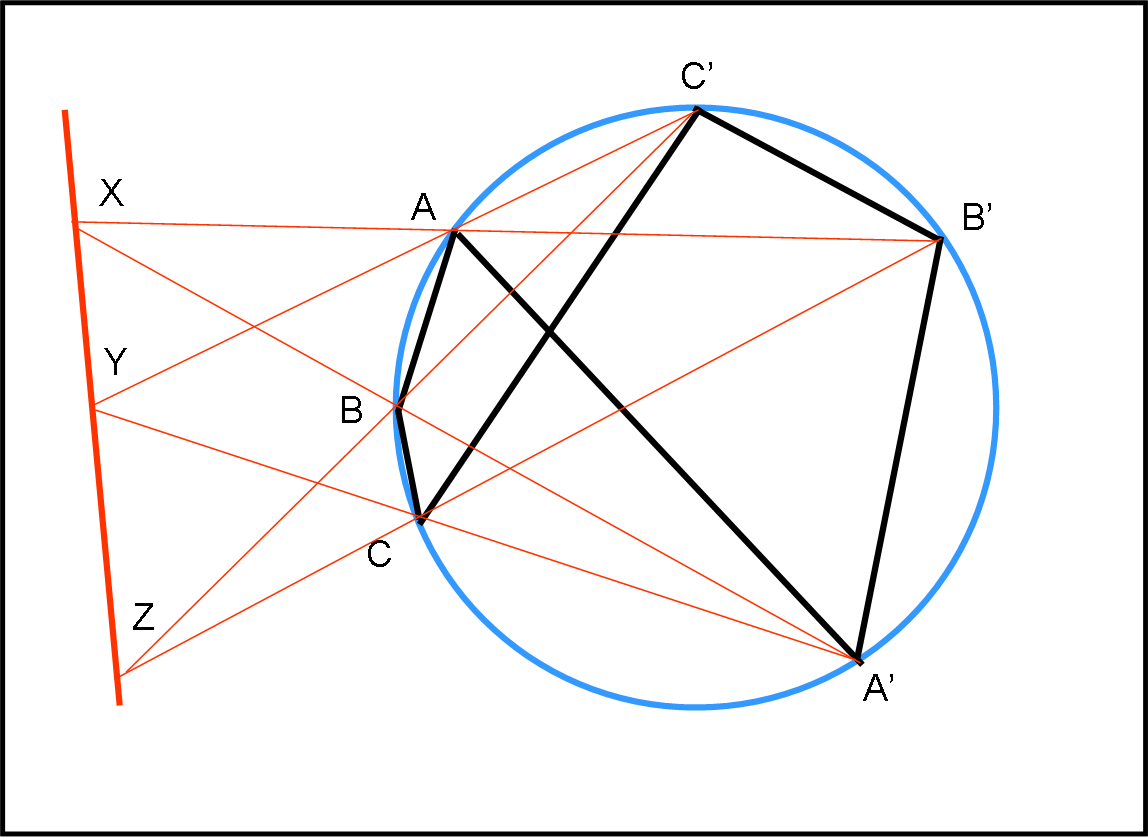
Continuando a ragionare su intersezioni di punti opposti otteniamo facilmente le rette proposte dal quiz. Ovviamente, la strana forma dell’esagono finale comporta una retta esterna al cerchio… La soluzione è riportata nelle Fig. 4, 5 e 6
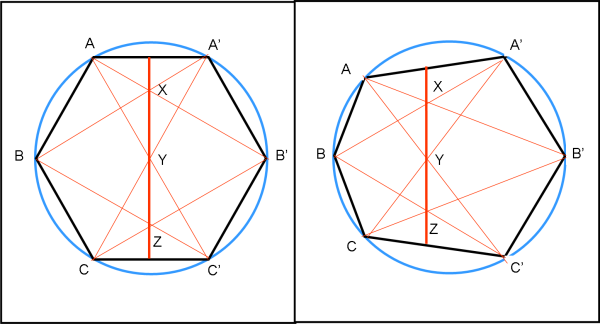
Bene, con questo quiz didattico, abbiamo aperto le porte alla geometria proiettiva non ci resta che descriverla in modo estremamente semplificato e farne la storia applicandola all’evoluzione della storia dell’arte.





