Categorie: Matematica Quiz
Tags: due uguale a zero numeri immaginari quiz
Scritto da: Vincenzo Zappalà
Commenti:38
QUIZ "immaginario": 2 = 0 *
Questo quiz è relativamente semplice per chi già conosce i numeri immaginari. Per chi non li conosce ancora, può servire come breve introduzione, dato che, forse, è arrivata l'ora di parlarne...
Non mi resta che scrivere delle relazioni che sembrano ineccepibili... eppure il risultato è alquanto imbarazzante.
2 = 1 + 1
2 = 1 + √1
2 = 1 + √((-1)(-1))
2 = 1 + √(-1) √(-1)
2 = 1 + (i)(i)
2 = 1 + i2
2 = 1 + (- 1)
2 = 1 - 1 = 0
Beh... il risultato sembra leggermente sbagliato, eppure...
Vi chiedo: dove sta ESATTAMENTE l'errore che ho commesso? Non cercate in rete, però...
38 commenti
La radice quadrata di 1 da come risultato ±1. E' del tutto evidente che se prendiamo come valore -1 (come si evince dalla 3° espressione) il risultato della 2° espressione è 0, in accordo con il risultato finale.
e quindi sarebbe giusto?
scrivere (-1) (-1) = + 1
non è un errore...
Credo che Cesare intenda dire questo:
Se nella prima riga appare +1, allora , nella seconda riga , la radice valida deve essere +1 ( e non -1)
Quindi nella terza riga va scritto , sotto radice, ( +1)(+1) invece di (-1)(-1).
Per effetto di questa subdola sostituzione si arriva al risultato assurdo 2 = 0.
Caro Enzo premetto che non conosco i numeri immaginari.
Quello che non mi convince è questo passaggio:
2 = 1 +√((-1)(-1))
2 = 1 +√(-1) √(-1)
Poiché (-1)(-1) = +1, qui viene tradotto nel prodotto di due radici quadrati di un numero negativo:
√(-1) √(-1)
Presumo, che la radice quadrata di -1 sia un numero immaginario...
Tu prosegui così:
2 = 1 + (i)(i)
2 = 1 + i²
2 = 1 + (- 1)
presumo che (i)² sia un numero immaginario (nel caso in esame √(-1) √(-1))..
ma se 2 = 1 + i², qualunque sia il segno di (i) il suo quadrato dovrebbe essere un numero positivo:
quindi:
2 = 1 + (+1) = 2
Comunque non conoscendo i numeri immaginari, potrei sbagliarmi di grosso...
Paolo
caro Paolo,
per uno che non conosce i numeri immaginari non potevi fare di più...
purtroppo devo dirti che l'unità immaginaria (i) è caratterizzata dall'essere il numero il cui quadrato è uguale a -1, per cui i2 = -1
caro Mau,
da che mondo è mondo (o quasi) la radice di 1 vale 1 e quindi la seconda riga è giusta (ho solo sostituito un valore con uno che è esattamente uguale, ossia ho scritto radice di 1 al posto di 1). La terza riga è sicuramente giusta dato che 1 è sicuramente uguale a -1 moltiplicato per -1... ho solo usato uguaglianze...
seguendo il tuo ragionamento
1 = √1 = √(-1*-1) = √-1 * √-1 = i * i = i^2 = -1 . quindi 1 = -1
Ammesso che 1 = √1 = √(-1*-1) sia corretto ( lo hai appena detto anche tu )
e lo sia anche √-1 * √-1 = i*i =-1 (proprietà dei numeri complessi)
significa che l'errore si trova in questo passaggio : √(-1*-1) = √-1 * √-1
E questa è la risposta alla tua precisa domanda :dove sta ESATTAMENTE l'errore che ho commesso?
Ora che abbiamo trovato il "dove" resta da spiegare il "perché" ( non fa parte dalla domanda ma è interessante)
La radice del prodotto di due numeri è uguale al prodotto delle radici di quei due numeri solo se i due numeri sono positivi. Nel campo dei numeri reali non esiste la radice di numeri negativi , quindi non possiamo scindere la radice del prodotto √(-1*-1) nel prodotto delle radici √-1 * √-1.
A mio parere l'operazione non lecita è il passaggio dalla 2a alla 3a riga.
Già da questa operazione nasce il risultato paraddossale finale.
L'operazione non è lecita perché contraddice il primo passaggio.
In generale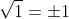
, ma in questo caso abbiamo già scelto una delle due possibilità nel primo passaggio 
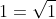e dobbiamo mantenere la coerenza.
Se volessimo mantenere le due possibilità dovremmo scrivere
Scusa Fabry... ma tu vorresti dire che non è plausibile scrivere (-1)(-1) = 1 ? A me sembra proprio di sì....
non dico altro...
Di per se è normalmente lecito. Qui però lo combiniamo con la radice quadrata utilizzando nella stessa espressione contemporaneamente le due soluzioni della radice.
Forse si vede meglio con un numero diverso da 1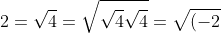(-2)}=-2)
o più banalmente diciamo che se sono vere, come sono vere,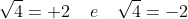
sarebbe vero anche che 
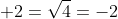che non è vera.
Stiamo utilizzando contemporaneamente i due possibili valori della radice di 4, è questo che non è lecito.
Nel nostro caso(-1)}=-1)
o più semplicemente
Aggiungerei questa considerazione: Enzo diceva "scrivere (-1) (-1) = + 1 non è un errore" e questo ci trova tutti d'accordo.
Ora, anche l'uguaglianza delle radici quadrate dei due termini dovrebbe essere valida, quindi:
e non è un errore neanche scrivere(-1)&space;}&space;=&space;\sqrt{(+1)(+1)})
e "dovrebbe essere possibile" (?) scrivere anche che
con la improbabile conseguenza che
quando invece sappiamo che 
meditate gente, meditate...
Il commento di Fabrizio è come sempre interessante e ha questa implicazione ...
Se b=a e b =c, è sempre lecito dedurre che a = c ?
Se b ammette due valori diversi , come nel caso della radice , non posso poi dire che i due valori sono uguali.
La proprietà transitiva non è sempre rispettata, ma dipende dalla relazione
il.problema proposto non è banale; dirò che in linea di massima sono d accordo con Maurizio, soprattutto sul punto incriminato. Si dimostra immediatamente per assurdo che quell uguaglianza fra radicali non può essere vera. Ma manca una dimostrazione diretta.
La dimostrazione diretta forse potrebbe essere ottenuta trasferendo sul piano complesso queste relazioni. Non so però quanto questo possa essere compatibile con il singolo asterisco dato al quiz.
La relazione(-1)}=?)
può essere scritta come
Per 1 vale anche la relazione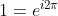
.
Possiamo quindi scrivere(-1)}=?)
come:
Ma in questo caso non possiamo uguagliarlo a 1 come abbiamo fatto sopra sfruttando il fatto che 0 diviso 2 è sempre 0, qui
Possiamo quindi scegliere per 1 diverse rappresentazioni nel piano complesso, ma poi dobbiamo essere coerenti con la scelta.
Argomenti diversi inseriti in una funzione possono dare uguale risultato. Ciò non significa che gli argomenti diventino uguali.
questo non significa che
, da cui avrei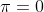 
Analogamente
questo non significa che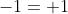
da cui avrei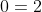 
Altrimenti, mettendo perversamente insieme i due risultati, potrei dire che , essendo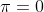
e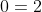 
, ne consegue che 
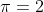, conclusione già dimostrata fallace , recentemente , qui
Seguendo la via della rappresentazione sul piano complesso la sequenza di passaggi proposti nel quiz dovrebbe essere
In rosso è evidenziato dove le sequenze divergono.
Per chi conosce i numeri immaginari, l'errore è banale e deriva da un proprietà delle radici quadrate. Una certa operazione vale solo e solo se entrambi i fattori sono positivi. Altrimenti può capitare questo:
SI SI SI NO SI
come diceva il buon Oreste...
i Si e i NO non sono in linea... riscrivo bene la ragione:
si può fare √a √b = √(ab) se e solo se a e b > 0
Avrei due domanda
Nel caso a o b o entrambi fossero negativi c'è una regola alternativa che permette l'operazione ?
Nella sequenza^2}=-1)
, che è evidentemente sbagliata, quale regola è infranta? Non mi sembra sia quella della scomposizione della radice.
si, però siamo nell'ambio dei numeri complessi. in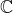
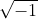esiste.A dirti la verità si dovrebbe affrontare la problematica lì, come ha cercato di fare Fabrizio. Il tutto non è ancora chiaro per me, anche se :
supponendo per assurdo che\cdot&space;(-1)}=\sqrt{-1}\cdot&space;\sqrt{-1})
(in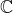 
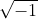esiste, quindi posso provare a scrivere quell'uguaglianza)
avremmo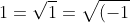\cdot&space;(-1)}=i\cdot&space;i=i^{2}=-1)
che è appunto assurdo. Quindi\cdot&space;(-1)}\neq&space;\sqrt{-1}\cdot&space;\sqrt{-1})
In pratica ho isolato l'unico passo falso della dimostrazione, e ho usato l'assurdo per arrivare alla conclusione.
Io vorrei però qualcosa che anche in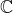
mi vieti (in R senz'altro perchè 
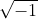non esiste) di scrivere :
In realtà bisogna sempre stare molto attenti a scrivere radici di numeri negativi...
Ad esempio, se volessimo usare i numeri immaginari, sarebbe meglio scrivere:
2 = 1 + 1 = 1 + (-1)(-1) = 1 + i2 i2 = 1 + i4 = 1 + 1
La regola che ci permette di non correre rischi di assurdità è quella di non usare mai √(-1) ma direttamente i.
L'ultimo passaggio che tu fai uguaglia le regole delle radici di numeri positivi con le regole delle radici di numeri negativi, il che non è vero...
Ti consiglio di leggere wikipedia (una volta tanto...) riguardo a radice quadrata... è spiegato abbastanza bene.
Comunque, la faccenda è molto sottile ed è per quello che si usa il numero i al posto di radice di meno uno, dato che quest'ultimo creerebbe ambiguità pericolose.
penso bisogni dimostrare che in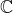
la formula:
non valga in generale, ma probabilmente solo quando a e b sono numeri reali positivi, o quando hanno segni discordi. Per rendersene conto basta fare la radice di due numeri complessi e poi la radice del prodotto. I calcoli sono però complessi per un numero con parte reale e immaginaria.
sappiamo già che per a=b=-1 non è vera; infatti\cdot&space;(-1)})
, mentre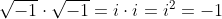 
inoltre questo è già sufficiente a risolvere il quiz. Nel quiz manipoliamo dei numeri e usiamo questo risultato,\cdot&space;(-1)}=\sqrt{-1}\cdot&space;\sqrt{-1})
come se fosse vero; in realtà essendo falso non posso procedere oltre.
sono pienamente d'accordo con Umberto
Umberto, per arrivare alla relazione sbagliata +1=-1 non mi sembra necessario passare per la scomposizione della radice e per i.
Ci deve essere qualcosa di sbagliato già in questa sequenza.
Sul quiz già nel post precedente mettevo in discussione questo passaggio (che noto è stato messo in discussione da tutti):
√((-1)(-1)) = √(-1) √(-1)
Non conoscendo i numeri immaginari mi chiedevo:
se (i)² = -1
a me sembra, per usare una similitudine con un vettore, un po’ come se si utilizzasse il quadrato del modulo e la moltiplicazione dei segni diversi fra loro, ossia:
(+1) (– 1) = - 1
(+) (-) 1² = - 1
Ma sicuramente mi sbaglio…
Paolo
però non è. Quello che ha scritto Vincenzo nel testo. Sarebbe un altro quiz. In tal caso ci fermeremmo qui, perché sai bene che é sbagliato, e non più avanti.
poi penso che come semplificare l esponente con la radice sia lecito come regola quando il numero sia positivo. In ogni caso davanti alla radice ê sottointeso il segno più e cosi deve restare. Se non conoscessimo il numero dentro parentesi dovremmo prendere il valore assoluto
Umbero, è vero che non coincide interamente con quanto scritto da Enzo, però coincide con la prima parte della sequenza.
Mi sembra che già in questi passaggi ci possa essere un errore.
in questi due? Per me no.
Scusa Umberto, in che senso non è quello che ha scritto Enzo nel testo?
Il passaggio nel quiz è il seguente:
2 = 1 +√((-1)(-1))
2 = 1 +√(-1) √(-1)
È evidente che in questo passaggio è stato semplicemente scomposto
√((-1)(-1)) = √(-1) √(-1)
Ma tale scomposizione origina un risultato differente rispetto alla partenza, trattandosi di radici quadrate di numeri negativi.
Su quanto dice Fabrizio, se non ho compreso male, mi sembra che lui metta già in discussione il passaggio precedente.
Se non ho capito male:
2 = 1 + 1
2 = 1 + √1
Ma √1 = ± 1
Se considero solo il risultato positivo, l’eguaglianza si mantiene:
2 = 1 + 1
ma se considero il risultato negativo l’eguaglianza non si mantiene:
2 = 1 - 1
Paolo
Vincenzo non ha scritto la radice del quadrato di -1 come Fabrizio
Verifichiamo se ad ogni passaggio i conti tornano....
2 = 1 + 1 Questa è la prima espressione.
2 = 1 + √1 (la radice di 1 sostituisce il +1 nella prima espressione ? SI )
2 = 1 + √((-1)(-1)) ( il valore √((-1)(-1)) sostituisce il +1 nella prima espressione ? SI)
Adesso arriviamo a questo passaggio ...
2 = 1 + √(-1) √(-1) (il valore √(-1) √(-1) sostituisce il +1 nella prima espressione ? NO, vale ì*ì = -1.
Questo è il punto.
in qualche vecchio libro si trova scritto:
la radice del prodotto é uguale al prodotto delle radici a patto che esse esistano. Naturalmente nel campo reale. Sembrerebbe di poter estendere tale regola nei numeri complessi, in quanto li esistono le radici dei numeri negativi. Ma cosi non é. Non mi ero mai posto il problema, calcolare la radice di un numero complesso implica un procedimento alquanto complicato. Conviene sempre fare prima il prodotto.
Detto in altre parole...
tutto nasce dal fatto che
(2)2 = 4
(-2)2 = 4
posso fare il quadrato di un numero positivo o negativo, il che vuol dire che esistono due numeri che danno lo stesso quadrato. Allora potrei dire che √4 = +/- 2. Ma questo NON E' VERO, perché porterebbe ad un'ambiguità, ossia alla possibilità di usare o un numero o l'altro (e ciao calcoli algebrici...). Invece la radice di 4 è solo e soltanto + 2. Il che significa imporre una sola possibilità. Infatti, nella definizione di radice quadrata si dice: "la radice quadrata di un numero n è quel numero POSITIVO m, tale che il suo quadrato sia n".
In pratica, non vale in campo complesso la proprietà √(A·B)=√A·√B.
In particolare, se A e B sono numeri reali negativi, la loro fase è 180°: quindi, siccome estraendo la radice quadrata la fase si dimezza, √A e √B hanno fase 90°. Inoltre, moltiplicando i risultati, le fasi si sommano, ottenendo come risultato (√A·√B) un numero con fase 180°. In altre parole, un numero reale negativo o nullo.
Al contrario, moltiplicando prima A e B si ottiene, per lo stesso motivo, un numero con fase nulla (180°+180°=360°, che è equivalente a 0°). Estraendo radice, infine, si ottiene un numero con fase nulla (0°/2=0°) moltiplicandoli le fasi si sommano ed estraendo radice si dimezzano, la fase di √(A·B) è (0+0)/2=0. In altre parole, √(A·B) è un numero positivo o nullo.
Quindi, a meno che A o B sia nullo (nel qual caso la fase sarebbe indeterminata), l'uguaglianza √(A·B)=√A·√B (da cui deriverebbe, se fosse applicabile, √((-1)·(-1))=√(-1)·√(-1)) non è valida.
Il tutto, utilizzando come radice quadrata quella principale.
il tuo commento è molto interessante, caro Marco... purtroppo, non abbiamo mai parlato di numeri complessi e quindi pochi lettori sanno cos'è la "fase". Prima o poi affronteremo l'argomento... Grazie!
Diciamo che un numero complesso a+ib si può rappresentare in un piano cartesiano dove sull'asse orizzontale viene rappresentata la parte reale a e sull'asse verticale quella immaginaria: in pratica a+ib è associato al punto P di coordinate (a;b). Si chiama fase (o anche, talvolta, argomento o anomalia) del numero a+ib l'angolo θ compreso tra il semiasse positivo delle x e la semiretta OP (dove O è, ovviamente, l'origine del sistema di riferimento). Esiste una convenzione secondo cui la fase θ deve essere tale che 0°≤θ<360°, anche se credo che quella convenzione più usata sia -180°<θ≤180°. Per esempio, per i numeri reali positivi θ=0°, mentre per quelli negativi θ=180°. Nel caso di i θ=90°, mentre per -i θ=-90°.
grazie Marco!
Anche se è passato un anno dall'ultimo commento volevo solo aggiungere il seguente concetto: prima di fare l'estrazione della radice (in questo caso quadrata) dovrebbe essere sempre specificato se siamo nell'insieme dei reali oppure dei complessi infatti:
se siamo in R allora la radice (se esiste) è unica ed è quella positiva
se siamo in C allora le radici esistono sempre e sono 2 (se la radice fosse quarta allora sarebbero 4 e così via)
Alla luce di questa premessa, dobbiamo necessariamente distinguere i due casi:
Caso dei reali: 1=sqrt(1)=sqrt[ (-1) * (-1) ]=sqrt(-1)*sqrt(-1) e qui mi devo fermare perchè l'ultima uguaglianza non ha senso in R
Caso dei complessi: 1=sqrt(1) e qui mi devo fermare immediatamente perchè in C non posso dire che sqrt(1)=1 perchè è anche vero che sqrt(1)=-1
Scusatemi se ho ripetuto dei concetti già espressi nei precedenti commenti.