Nei commenti del QUIZ, potete trovare la soluzione espressa in modi anche diversi tra loro. Noi ci limitiamo a quella -forse- più semplice che necessita delle minime conoscenze dello studio di una funzione.

Prima dell’intervento del diabolico Nobody il percorso era completamente rettilineo e si sviluppava per 2 km giusti giusti (il segmento AB).

La comparsa del muro invisibile pone un serio problema che potrebbe essere affrontato in vari modi. Il primo sarebbe quello di “sperare” di essere fortunati, ossia arrivare sempre fino a C e poi decidere sul momento (Fig. 1). Se il muro non c’è si può proseguire fino a B e compiere il percorso di 2 k. Se, invece ci fosse il muro… pazienza: ci si recherebbe fino a M e poi si proseguirebbe verso B lungo la congiungente MB (non vale certo pena di ridiscendere fino a C e proseguire fino a B…).

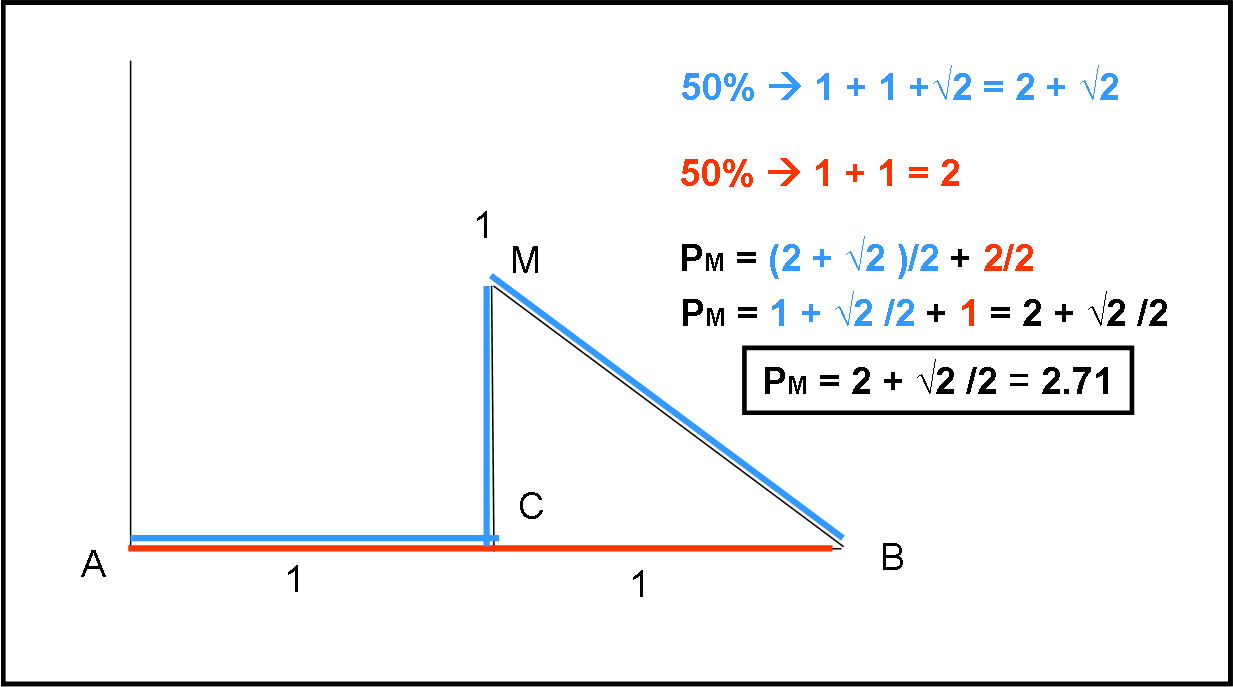
Ciò che succede allora è che per il 50% delle volte il percorso P₁ varrebbe

P₁ = AC + CB = 1 + 1 = 2

E per un altro 50%, varrebbe P₂, ossia:

P₂ = AC + CM + MB = 1 + 1 + √2 = 2 + √2

Il percorso medio P_M, vale, perciò

P_M = (P₁ + P₂)/2 = 2/2 + (2 +√2)/2 ≈  1 + 1 + 0.71 = 2.71 km

Un’altra possibilità (un po’ troppo sbrigativa) sarebbe quella di non curarsi del muro e andare ogni giorno da A a M e poi da M a B (Fig. 2).

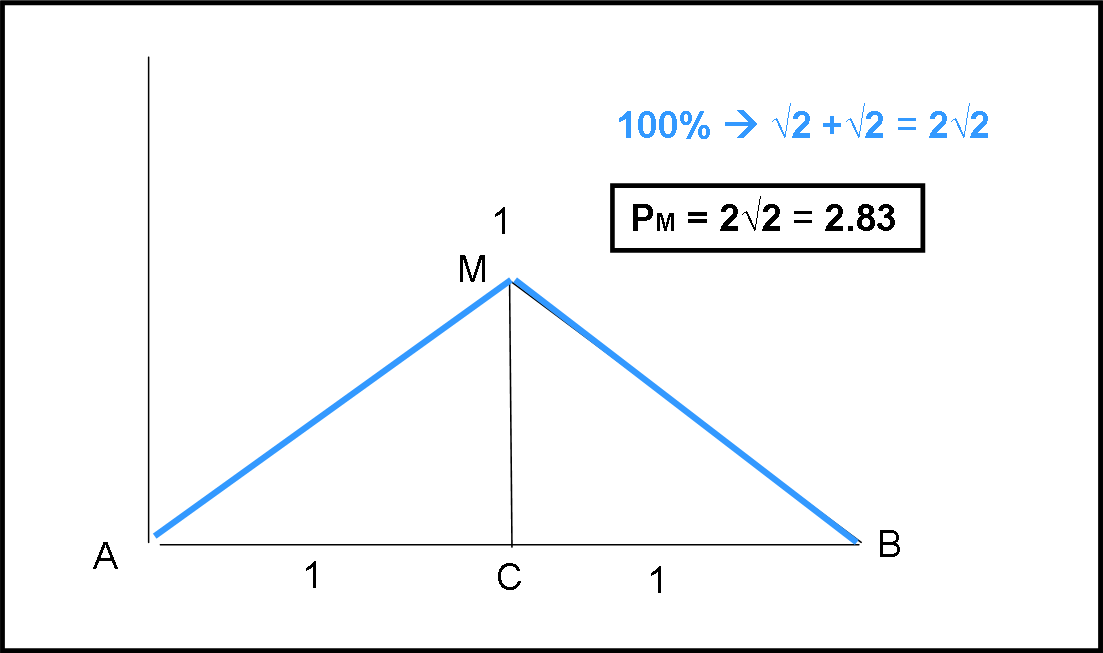
Un bel modo per “snobbare” Nobody, ma decisamente più lungo. Il percorso sarebbe sempre lo stesso e varrebbe:

P = AM + MB = √2 + √2 ≈ 1.41+ 1,41 = 2.83 km

Non ne vale la pena allungare di così tanto e i Pappidi pensano a un qualcosa di meno faticoso. L’idea è quella di andare da A fino a un certo punto P del muro (CP = y) e poi decidere il da farsi, come per la prima ipotesi: o proseguire per M e poi andare da M a B, oppure (se il muro non si è alzato) proseguire lungo MB (Fig. 3)

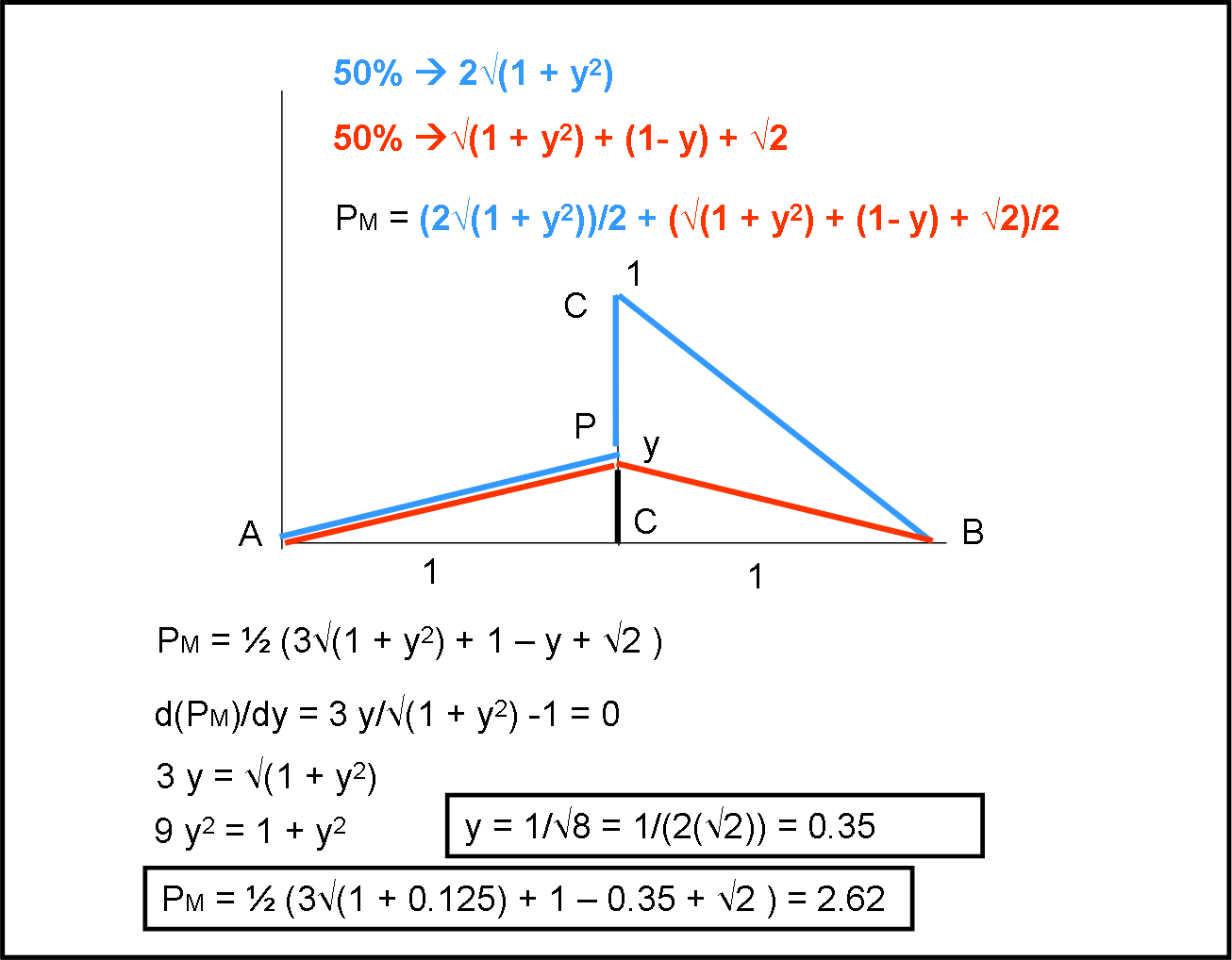
L’idea è sicuramente buona, ma come scegliere il punto P? Abbiamo già visto che non può essere né proprio C (y = 0) e nemmeno M (y = 1), ma un punto intermedio. Vediamo come si può scrivere il percorso in funzione della variabile y. Se non si alza il muro si ha (nel 50% dei casi):

P₁ = AP + PB = √(1 + y²) + √(1 + y²) = 2√(1 + y²)

Se si alza il muro (restante 50% dei casi):

P₂ = AP + PM + MB = √(1 + y²) + (1 – y) + √2

Il valore medio sarebbe, perciò:

P_M = ½(P1 + P2) = ½(2√(1 + y²) + √(1 + y²) + (1 – y) + √2)

P_M = ½ ( 3√(1 + y²) + (1 – y) + √2)

Non ci resta, adesso, che decidere per quale valore di y il valore P_M diventa minimo.

Tuttavia, è come se avessimo:

P_M = f(y)

E sappiamo bene che il minimo di una funzione si ottiene per il valore di y tale da azzerare la derivata prima della funzione. Non dobbiamo fare altro che derivare la f(x) e poi uguagliarla a 0 e vedere quale valore di y soddisfa questa relazione.

df(y)/dy = ½ d(3√(1 + y²) + (1 – y) + √2)/dy = 0

Ovviamente, ½ può essere fatto uscire dalla derivata (è una costante) e , oltretutto non è certo uguale a zero, per cui possiamo scrivere soltanto:

d(3√(1 + y²) + (1 – y) + √2)/dy = 0

Ricordiamo subito che √(1 + y²) è una funzione di funzione, del tipo m(g(y)), e quindi è necessario moltiplicare la derivata della funzione m per la derivata della funzione g.

3(2y/(2√(1 + y²)) – 1 = 0

3y/(√(1 + y²))  = 1

3y = √(1 + y²)

Quadriamo entrambi i membri

9y² = 1 + y²

8y² = 1

y = 1/√8 ≈ 0.35

Basta sostituire questo valore nella relazione che esprime il percorso P_M, per ottenere quello minimo:

P_M (minimo) ≈ ½ ( 3√(1 + (0.35)²) + (1 – 0.35) + √2) = 2.62 km

Decisamente più corto degli altri, come volevasi dimostrare.

Ai Pappidi non la si fa…

 

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!