Un quiz.. Diabolico!
Perchè diabolico? perchè la sua concezione sembra stata ispirata dal diavolo. Tipo una domanda posta ad un Faust-matematico per salvare l'anima. Un quiz apparentemente difficile, ma dalla soluzione semplicissima. Ognuno può seguire vari ragionamenti.. e potrebbero anche non servire calcoli complicati .
Considerate la figura:
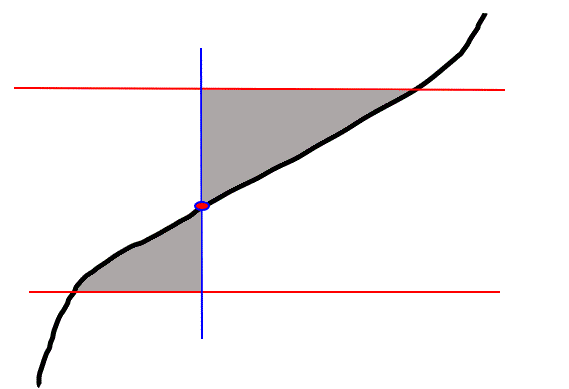
Abbiamo a che fare con una funzione monotona crescente. Aggiungiamo poi che è anche continua, affinché non possano generarsi ambiguità, e ovunque definita.
Il grafico di tale funzione è intersecato da due rette orizzontali in colore rosso, fissate, e con una certa distanza fra loro. Per ogni punto sulla curva è possibile tracciare una retta verticale, che assieme alle due rette orizzontali e alla curva delimita due aree. Eventualmente, una delle due aree può essere degenere.Trovare il punto sulla curva in modo che sia minima la somma delle due aree grigie limitate dalle rette orizzontali, dalla curva e dalla retta verticale blu che passa per il punto.
PS:







66 commenti
Poiché non è data l'equazione della curva, intuisco che la risposta sia valida a prescindere da quest'ultima, cioè vale per qualsiasi curva, purché questa sia monotona, crescente, continua e ovunque definita. Dopo avere stabilito le due rette orizzontali rosse, per esempio y=1 e y=3, ho così cominciato a provare con una curva semplice, cioè una retta di equazione y=1/2 x e ho trovato analiticamente il valore della x che mi annulla la derivata prima della somma delle due aree in questione. Poi sono passato ad una parabola, di equazione y = 1/2 x^2 e ho ripetuto il ragionamento. Idem per una curva di equazione y = 1/2 x^3. A questo punto mi sono accorto che l'ordinata del punto di intersezione tra la retta verticale blu e la curva data non cambiava passando da una curva all'altra. Infatti ho voluto provare infine con una curva di equazione y=ln(x) e con una curva di equazione y = radq(x) e ho verificato che succede la stessa cosa. Cambia l'ascissa del punto punto di intersezione tra la retta blu e la curva data, ma non l'ordinata. In particolare, l'ordinata di tale punto risulta essere sempre a metà strada tra le due rette rosse. Mi verrebbe quindi da azzardare che tale punto si trova semplicemente tagliando la curva (qualsiasi) con la retta orizzontale posta a metà tra le due rette rosse.
Se è così, mancherebbe solo una dimostrazione rigorosa e generale ...
non mi sembra una cattiva idea Arturo
Forse ci sono.
Sia y=f(x) l'equazione della curva (generica).
Indico con a l'area a sinistra della retta blu e con b quella a destra. Indico con A il punto di intersezione della curva con la retta rozza inferiore e con B quello con la retta rossa superiore. Indico con P il punto di intersezione della curva con la retta blu. Siano x(A) , y(A) , x(B), y(B) le coordinate (considerate note) dei punti A e B. Siano x, y le coordinate , ignote, del punto P.
Ricordando il significato geometrico dell'integrale definito, posso scrivere:
Infatti, l'area a è la differenza tra l'area sottesa dalla curva tra A e P e il rettangolo avente base (x-x(A)) e altezza pari a y(A). Stesso ragionamento per l'area b.
La somma delle aree , svolgendo i calcoli, è dunque data da:
cioè, mettendo in evidenza la x, :![a+b=\int_{x(A)}^{x}f(x)dx-x[y(A)+y(B)]+x(A)y(A)+x(B)y(B)-\int_{x}^{x(B))}f(x)dx](http://latex.codecogs.com/gif.latex?a+b=\int_{x(A)}^{x}f(x)dx-x[y(A)+y(B)]+x(A)y(A)+x(B)y(B)-\int_{x}^{x(B))}f(x)dx)
Poiché devo trovare il punto P per il quale si ha la minima somma delle aree, calcolo la derivata prima della suddetta espressione, ricordando il teorema fondamentale del calcolo integrale:
cioè:
Poiché tale derivata deve annullarsi, ottengo:
cioè:
Dunque, l'ordinata del punto P è a metà strada tra le due rette rosse.
vedrò Arturo anche se so che quello che scrivi ê senz'altro valido.volevo solo dire che anche chi non conosce il calcolo differenziale può risolvere il quiz. Comunque grazie per la risposta.
Se al posto della curva studio una poligonale che la approssima, in ogni tratto RETTILINEO trovo sempre che la linea che determina localmente la minimizzazione della somma delle due aree è a metà del dislivello in quel tratto, cosa che ha già verificato Arturo nel primo commento.
Mettendo insieme tutti i risultati nei vari tratti, ottengo che la limea blu si troverà a metà del dislivello totale tra le due linee rosse.
Il punto cercato è equidistante dalle due rette.
Ci si può arrivare guardando la figura, in cui il punto rosso è un po troppo basso e quindi a sinistra del punto ottimale.
Immaginando infinitesime strisce verticali grige che compongono l'area grigia, si vede che
Quindi conviene far scorrere il punto rosso verso dx in modo da considerare le strisce corte a sx e non quelle lunghe a dx.
Punto ottimale quello in cui sia a sx che a dx sono pari alla metà della distanza.
maledetti!!! ma voi lavorate di notte... io dormo...uffa!
Ti sbagli, Enzo, anche io dormo , lo prova il fatto che non capisco cosa ho scritto in stato di sonnambulismo questa notte.
Sarà stato un fenomeno diabolico....
grazie amici.. Aspettiamo anche gli altri, c e ancora spazio per i commenti.
infatti io avevo previsto un unico approccio e invece ne abbiamo già tre.quindi senz altro ce ne sono degli altri. Scusa Maurizio quando puoi fare un disegno esplicativo?
la tua idea Mauro mi piace, potresti chiarire meglio ai lettori cosa significa quel "conviene". Ricordiamoci la definizione di minimo.
Purtroppo non ho tempo da dedicare al bel quiz che si può risolvere sicuramente in modo puramente geometrico...
Conviene considerare per prima una retta che comporta un bel rettangolo che la retta divide a metà. I due casi estremi equivalgono a una somma delle aree uguali a mezza area del rettangolo. il caso di minima somma è ovviamente una linea che taglia a metà il rettangolo, dato che si ottiene solo 1/4 dell'area del rettangolo. In questo caso, però, la divisione comporta sia la metà del delta y, sia la metà del delta x.
Tuttavia, prendendo una curva qualsiasi si possono sempre costruire dei rettangoli e dei ribaltamenti della curva che pongono limiti ben chiari ai valori delle aree e fanno preferire, così a occhio per adesso, la metà del dy alla metà del dx.
Se qualcuno vuol provare questa strada... (magari è già stata adottata... non ho voluto leggere le risposte precedenti...). Magari nel pomeriggio ho più tempo... (ho il garage da sgomberare e un paio di articoli d terminare...).
Poi si può sempre usare il metodo della costruzione diretta e del taglia e confronta....
grazie Vincenzo, comunque non c'è fretta. Sono proprio curioso di scoprire come avrebbe risolto Euclide questo problema
Caro Umberto, lascerei da parte il mio commento precedente che, come spiegato ad Enzo, è frutto del dormiveglia notturno. Se mi torna in mente quello che intendevo dire te lo farò sapere.
Invece vorrei postare un disegno relativo alla idea di Mauro che mi sembra molto buona.
La figura al centro mostra la linea verde a metà tra le due rosse. In questo caso la linea blu delimita le due aree da sommare (quella azzurra, sotto la funzione, e quella gialla sopra) Da notare che l'altezza finale della zona azzurra è identica alla altezza iniziale della zona gialla.
Nella figura a sinistra, la linea verde è spostata più in basso della metà e la linea blu si sposta a sinistra rispetto a prima. l'area gialla aumenta della superficie che vediamo e l'area azzurra diminuisce in misura minore, perché ad ogni ordinata verso sinistra corrisponde una crescita di altezza per la zona gialla e una corrispondente diminuzione di altezza nella zona azzurra. In definitiva l'area globale aumenta.
Nella figura a destra, la linea verde è spostata più in alto della metà, conseguentemente la linea blu passa a destra. Anche qui le due aree gialla e azzurra si modificano. Ma questa volta è l'area azzurra ad aumentare più di quanto diminuisca l'area gialla. Il risultato è comunque un aumento dell'area totale.
Dato che ogni spostamento a sinistra o a destra comporta un aumento dell'area totale rispetto alla posizione intermedia, questa posizione rappresenta la situazione di minimo cercata.
Spero di avere interpretato correttamente quello che ho letto nel commento di Mauro e di non avere introdotto più confusione che chiarezza.
qualcosa del genere...
va bene...a più tardi... ho paura di spostare qualcosa e vedere uscire un dinosauro... l'epoca è quella (ossia quando ho messo a posto l'ultima volta...)
più o meno così Maurizio; in effetti l'idea di Mauro è proprio buona. Chissà se esiste il modo di formalizzarla.
Il metodo di Arturo è accademico e rigorosamente ineccepibile; chissà se è possibile trovarne un altro che non faccia uso del calcolo differenziale-integrale. Comunque in ogni caso siamo quasi a cavallo.
Mi butto su una soluzione geometrica.
Ribalto la parte della figura a destra della linea blu e traslo questa parte in modo da far coincidere le linee rosse.
L'area che ci interesse è quella contenuta tra la linea di base e la nuova curva ottenuta.
L'area ottenuta posizionando la linea blu in un punto qualsiasi mi sembra che contenga sempre quella che otterrei posizionando la linea blu nel punto dove la curva iniziale divide in due parti uguali il segmento tra le due linee rosse. Quindi quest'ultima è la minima area possibile.
In questo momento non riesco a fare la figura. Provo più tardi a farla.
buona idea Fabrizio. Si, la figura serve senz altro
Fabrizio sta andando nel mio verso... L'unico modo per avere un ribaltamento completo della curva si ha sulla retta y mediana. O sulla x mediana... basta confrontare queste due... Nel caso rettilineo coincidono... Proverò più tardi...
bene
Ho cinque minuti di tempo...
Invece di far variare la x, faccio variare la y (deve essere la stessa cosa)...
Le due aree limite sono l'area interna alla curva (y = 0) (praticamente il suo integrale) e Area rettangolo - Area curva (y = ymax). Muovendo la y, ottengo le due aree richieste che sono sempre l'integrale della curva al di sopra della retta y fino al valore di x corrispondente alla y (y = f(x)) e nuovamente la differenza di aree tra quella del rettangolo (comparso tra x e xmax e y e ymax) meno l'integrale della curva a partire da x fino a xmax al di sopra di y. Potrebbe darsi che non ci sia bisogno di fare realmente gli integrali... In pratica c'è un rettangolo da togliere ogni volta rispetto ai casi degeneri...
Va beh... ci vorrebbe troppo tempo... lascio perdere...
Insomma, praticamente questa figura...
penso si possa trattare l'integrale o i suoi pezzi come valori k(x) o k(y) e risolverlo comunque...
Adesso devo proprio scappare... UFFA!!!!
ricordando il teorema fondamentale del calcolo integrale...
Spero che questa animazione illustri quello che ho scritto questa mattina.
Ribalto la parte della figura a destra della linea blu e la traslo in modo da posizionarla sulla linea rossa alla base. L'area che ci interesse è quella evidenziata in giallo.
L'area scura che appare alla fine è quella ottenuta posizionando la linea blu nel punto dove la curva iniziale divide in due parti uguali il segmento tra le due linee rosse.
Comunque si posizioni la linea blu, l'area più scura sarà contenuta in quella gialla.
Il posizionamento della parte destra dell'area richiede solo una rotazione se si prende come asse la retta mediana tra le linee rosse.
Non c'è bisogno di integrali, ma solo di rettangoli...
La figura dovrebbe dimostrare che solo la linea mediana delle y risolve il problem, dato che è massima la somma di Q1 e Q2 (metà del rettangolo completo)
Non è proprio euclidea, ma poco ci manca!!
Ho buttato giù in fretta... ma, se non si capisce l'ordine delle relazioni, lo farò con più calma...
La prima figura è quella in cui (anche se non sembra) la riga orizzontale spessa è la mediana
bene bene mi piacciono questi approcci geometrici che non avevo considerato. Magari avrò bisogno di un commento riassuntivo. Poi aspetterò altre idee.
Mi sono accorto che non è corretto... devo sistemare meglio il legame tra A e S. La strada dovrebbe essere quella giusta... ma ci vorrebbe un po' di calma e io anche oggi sarò ultra preso... Se vuole aiutarmi qualcun altro...
....
Grazie Umberto,
cerco di spiegarmi meglio, ma senza usare nessuna formula.
Chiamiamo d-sup la distanza di ogni punto dalla retta superiore d-inf la distanza dalla retta inferiore.
(Per semplicità ipotizziamo la distanza delle due rette pari a 1)
L'estremo di sx avrà d-sup=1 e d-inf=0, mentre l'estremo di dx avrà d-sup=0 e d-inf=1.
Chiamiamo r-media la retta equidistante dalle due rette rosse. Il punto di intresezione tra r-media e la curva è il punto ottimale M (d-inf=d-sup=0.5)
Poichè le d-inf contribuiscono all'integrale inferiore, mentre le d-sup a quello superiore, e il nostro problema ci chiede di sommare l'integrale inferiore a sx di M all'integrale superiore a dx di M, dobbiamo considerare/sommare le d-inf finchè sono minori delle d-sup a sx, e le d-sup minori di d-inf a destra.
Il punto M è dove le d-inf e d-sup si scambiano di posto nell'essere le minori distanze.
non c'è fretta Vincenzo. Aspetto un commento riassuntivo come dicevo sopra.
ok Mauro se tu riuscissi a fare un disegno.. Sarebbe essenziale per questo tipo di quiz
Quello che conta nella figura sono solo i rettangolo Q1 e Q2. Essi ci dicono che la loro somma è massima quando la y è la mediana dato che vale proprio metà del rettangolo di partenza.
Bisogna quindi solo studiare l'andamento di una somma che è minima per la y mediana.
Ossia A1 + S1 + A2 + S2 è minima sicuramente.
Resta da dimostrare che è minima anche A1 + A2
Penso che basti scomporre ancora la differenza in rettangoli... ma devo scappare... no, non si può lavorare così... abbiate pazienza....
Pau o Harley completa tu in mia assenza....
Mentre aspettiamo la dimostrazione di Vincenzo completa, volevo fare il punto della situazione. A parte la rigorosa dimostrazione di Arturo, l'approccio che mi piace di più è quello di Mauro, rielaborato anche da Maurizio, pur non avendo ancora l'aspetto di una dimostrazione matematica. Sono certo poi che la dimostrazione di Fabrizio sia valida, ma mi permetto di chiedere se è possibile invece dell'animazione, fare una sequenza dei disegni con evidenziata anche la posizione della linea di mezzeria. La dimostrazione in questo caso è visiva, bisognerebbe se possibile aggiungere anche qualche ulteriore spiegazione per poterla capire meglio. Magari c'è chi l'ha capita meglio di me, che sono abbastanza scarso a livello di percezione visivo-spaziale.
Enzo, oggi , tra arrivi e partenze, la giornata se ne va via in aeroporto a Cagliari . Siamo tutti in giro senza PC.
Magari in serata si riuscirà a lavorarci spora. Intanto ci pensiamo ...
non c'è nessuna fretta Maurizio. Il quiz è stato pubblicato nemmeno da due giorni
intanto meditavo.. ancora una volta risulta vero il detto dei latini "in medio stat virtus" ...
Scusate ma a me sembra che se scorriamo l asfissia x verso x crescenti, l area di sinistra aumenta di un valore prop a f(x), mentre diminuisce a destra proporzionalmente a 1- f(x). L incremento netto è quindi proporzionale a 2 f(x) -1. Tale incremento sarà nullo per f(×) =1/2. Senza integrali ma soprattutto con uno stupido tablet che scrive quello che gli pare.
Questa volta penso proprio di non sbagliare… ma con i giorni che ho passato, tutto può essere. In realtà, la faccenda è di una tale banalità che mi sembra impossibile. Se ho sbgliato anche questa volta sbattetemi fuori dal Circolo!!
Parto con l’ipotesi che le aree minori siano quelle relative alla mediana delle y
Traccio una curva qualsiasi CRESCENTE e considero il caso di minima somma (lo devo provare però…)
Le due aree sono colorate in rosso e le ho spezzate in tre parti: A1, A2, A3.
Faccio la somma delle tre
S = A1 + A2 + A3
A2 è racchiusa nel rettangolo a linea spessa che è uguale a quello di sotto.
A2 = R – T
Posso scrivere:
S = A1 + R – T + A3
Adesso prendo un’altra qualsiasi retta parallela a y (le ho provate tutte e vale sempre)
Faccio di nuovo la somma delle tre nuove aree:
S’ = A1 + A2’ + A3
Ma
A2’ = R + T
S’ = A1 + R + T + A3
Per qualsiasi S’ posso fare la differenza rispetto a S:
S’ – S = 2T > 0
S’ > S
S ci regala la somma minima delle due aree (come nel caso della retta).
Mi sembra che il ragionamento di Leandro non faccia una piega...
Non penso ci sia modo più lineare, semplice e comprensibile da tutti per giustificare il risultato.
Non avevo letto Leandro ancora, ma mi sa che stiamo dicendo la stessa cosa...
non è vero che il.problema è banale. Se Arturo non avesse spianato la strada trovando la soluzione con il calcolo differenziale sarebbe ancora più difficile trovarla oltre che dimostrarla Scusa Leandro, ma come fa l'incremento di un area ad essere proporzionale al valore della funzione anche se crescente? Pensa ad una funzione asintotica..
La soluzione rigorosa formulata da Arturo non è certo una banalità, ma, nello stesso testo del quiz, si accenna ad una "soluzione semplicissima" , immagino intuitiva.
La regolarità della funzione, monotona crescente, continua e ovunque definita, suggerisce una possibilità di valutazione altrettanto semplice, e anche la figura, che interseca univocamente la linea inferiore e la linea superiore, incoraggia a pensare ad una soluzione geometrica elementare.
Per quanto riguarda gli incrementi e i decrementi delle aree, al variare della ascissa, rifacendomi a questa immagine , pubblicata in un precedente commento,
io li vedo ( nella prima e nella terza figura ) come "trapezi" , che hanno per base l'intervallo di variazione della x e come altezza il valore (intermedio) della f(x).
In questo senso, ritengo, vada letta la frase di Leandro, sulla proporzionalità delle aree alla f(x).
tutti i ragionamenti esposti sono validi Maurizio. Dicevo solo che l unico rigoroso dal punto di vista matematico é quello di Arturo .Ma ne troveremo un altro, ne sono sicuro.
Seguo l'invito di Umberto di esprimere la soluzione che ho proposto in modo più esteso e confidando di meno nell'intuito visivo.
Figura 1
Introduco un asse mediano tra le due rette rosse e traccio una seconda curva (verde) speculare alla curva considerata nel quiz rispetto a questo asse. Questa seconda curva ha 3 proprietà che ci interessano. Queste proprietà derivano direttamente dal modo con la quale l'abbiamo costruita e dal fatto che la prima curva è crescente e continua.
Le due curve si intersecano in un punto che si trova sull'asse mediano.
La nuova curva è sopra l'altra a sinistra del punto di intersezione ed è sotto a destra del punto di intersezione.
La terza proprietà che ci interessa riguarda le aree.
Figura 2a e 2b
L'area sovrastante la prima curva (fig.2a) è uguale a quella sottostante la nuova curva che abbiamo costruito (fig.2b). Questo è vero anche per porzioni di aree ottenute sezionando l'area totale con un segmento verticale (blu).
Da quanto detto sopra segue che l'area totale da considerare nel quiz (A1+A2 di fig.3a) è uguale ad A1+B2 della figura 3b.
Figura 3a e 3b
Ora vediamo come si presentano le nostre aree se scegliamo come retta verticale quella passante per l'intersezione delle due curve che abbiamo tracciato (fig.4a).
Figura 4a e 4b
Per confrontare le aree, in fig.4b sovrapponiamo le aree ottenute in fig.3b e 4a.
La figura è divisa in 3 parti delle due rette verticali che abbiamo utilizzato. Nelle parti a destra e sinistra le aree di fig.3b e 4a sono identiche. Differiscono invece nella parte centrale.
Per comodità chiamo f la curva originale del quiz e chiamo g la nuova curva (verde). Nella parte centrale l'area in figura 3b è limitata dalla nuova curva g mentre l'area di fig.4b è limitata dalla vecchia curva f.
Poiché siamo prima del punto di intersezione delle due curve ed f è una curva crescente e continua, allora g è sempre maggiore di f in questa sezione della figura. Vale a dire che in questo settore l'area di fig.4a e contenuta in quella di fig.3b. Poiché negli altri due settori le aree sono uguali, l'area totale di fig.4a e contenuta in quella di fig.3b.
Si può ripetere il ragionamento in modo analogo nel caso di retta verticale posta oltre il punto di intersezione con il medesimo risultato finale.
Ne segue che facendo passare la retta verticale (blu) nel punto di intersezione tra f e g si ottiene il minimo della somma delle due aree del nostro quiz.
Il tutto potrebbe essere tradotto in modo analitico utilizzando le funzioni f(x) e g(x).
mi farebbe piacere che qualcuno commentasse anche la mia soluzione grafica... grazie...
li sto rileggendo tutti.abbi pazienza sono tanti
Come già detto, il risultato deve valere per qualsiasi funzione crescente. Il che vuol dire che deve valere anche per la retta. In quel caso, bastano pochi triangoli rettangoli per stabilire che l'area minima si DEVE avere o per y mediana o per x mediana. La x mediana viene subito esclusa (varrebbe forse nel caso di una funzione decrescente... invertendo x con y), per cui basta provare che qualsiasi somma è maggiore di quella definita dalla y mediana. Per me è più che valida...
e' ovvio, che la soluzione rigorosa comporti l'utilizzo degli integrali e l loro proprietà... ma qui si cercava di dare soluzioni alternative, soprattutto geometriche e semplici... Oppure avevo capito male?
l intento sarebbe in questo momento di dare una soluzione generale senza usare gli integrali per qualsiasi funzione crescente.non dolo per la retta.
Ed è esattamente quello che ho fatto con l'ultima soluzione con figure accluse.... (la retta serve solo per sapere da dove partire, dato che la soluzione deve valere per qualsiasi funzione...)
bene. Abbi ancora un po di pazienza.
Il punto fondamentale che crea la banalità della soluzione è il fatto che la y mediana regala rettangoli uguali sopra e sotto, cosa che non fa la x mediana (a meno di non ruotare il tutto e usare funzioni decrescenti...).
Riprendo il commento di Enzo, di ieri pomeriggio in cui presenta la soluzione con le aree rosse, e il suo successivo commento in cui sottolinea la convergenza con la soluzione di Mauro.
Anche a me sembra che i due ragionamenti siano paralleli e si basino sulla analisi di cosa succede variando le coordinate del punto di separazione.
Il punto è che si fa una ipotesi sulla linea mediana e poi la si verifica. La cosa è legittima ma è diversa dal ricavare il risultato senza ipotesi priminari. E' forse questo che stai aspettando di vedere, Umberto?
si, bisognerà provare anche quello Maurizio. Vincenzo ho visto. Tu ti sposti a destra e trovi un area più grande. Lo stesso se ti sposti s sinistra?
Scusate ma non ci siamo.... la f(x) DEVE essere qualsiasi crescente e quindi può essere anche una retta. Se valesse solo per la retta, vorrebbe dire che per ogni f(x) ci sarebbe un valore diverso. Mi posso, perciò, permettere di lavorare solo con la retta per trovare il valore minimo.
Lavorando solo con la retta trovo che va bene sia la y mediana che la x mediana.
Attraverso la sola retta, mi accorgo di come tutto sia legato a un rettangolo che rimane uguale sopra e sotto (in verticale). Nel caso della retta il rettangolo è sempre tagliato perfettamente in due e una volta aggiunge un pezzo e una volta lo toglie.
La stessa identica cosa succede per qualsiasi f(x) crescente: c'è un pezzo da aggiungere e un pezzo da togliere, qualsiasi sia la funzione, dato che lei è sempre racchiusa dentro al famoso rettangolo, il 'perno di tutto.
Facendo qualsiasi prova (ma ne basta una, ovviamente) si conferma quanto ottenuto per la retta e si elimina la x mediana.
Non c'è bisogno di integrali ma solo di aree curvilinee e quindi era risolvibile perfettamente anche dai greci!
Temo che Umberto non abbia ancora afferrato appieno la generalità del rettangolo marcato in nero: lui è sempre quello, sia se preso prima o dopo il punto di mezzo delle y.
Cercherò di fare la trattazione completa partendo dalla retta...ma è di una banalità geometrica lampante. Basta avere il tempo di ragionarci sopra e oggi dovrei avercelo...
a dopo...
io penso di non essermi spiegato bene con la mia domanda. Tu nel primo disegno rosso parti con l'area minima.
Poi tracci una y parallela a destra e dimostri perfettamente che l'area aumenta. E se la parallela y la tracci a sinistra cosa fa l'area? Non mi sembra che il disegno sia simmetrico O forse per te è talmente ovvio che non vale la pena di farlo, o forse come dici tu non ho capito niente.
Come detto precedentemente è più che lecito che io usi una retta dato che si parla vagamente di una funzione qualsiasi e la retta lo è. Non può essere un caso particolare, altrimenti non varrebbe l'ipotesi di partenza f(x) qualsiasi!
E' immediato dimostrare quale sia la somma delle aree minime (basta sommare rettangoli e triangoli e un po' di Pitagora al limite (ed è ammesso!)).
Trovata questa situazione, vado avanti prendendo una retta più bassa e una più alta (così accontento Umberto ) e dimostro immediatamente, usando il famoso rettangolo e il triangolo T, che è veramente la somma di aree minima. Non ce n'era bisogno, ma la trafila mi serve per il passaggio alla curva e renderla più chiara. In pratica, DIMOSTRARE che nulla cambia anche se la f(x) è qualsiasi, ma crescente.
) e dimostro immediatamente, usando il famoso rettangolo e il triangolo T, che è veramente la somma di aree minima. Non ce n'era bisogno, ma la trafila mi serve per il passaggio alla curva e renderla più chiara. In pratica, DIMOSTRARE che nulla cambia anche se la f(x) è qualsiasi, ma crescente.
Ecco le figure per la retta:
dopo di che si possono usare le figure del commento precedente, dove non cambia niente, tranne che il triangolo T non è più un triangolo, ma è delimitato da un pezzo della curva f(x). Più banale di così...
Per me Euclide sarebbe contento...
caro Umberto,
il disegno non deve essere simmetrico, ma te l'ho dimostrato per la retta. Se vuoi posso farlo anche con la curva. Sopra o sotto che sia la retta che tracci le aree aumentano SEMPRE rispetto non a un'ipotesi, ma rispetto a una dimostrazione fatta con la retta che è anch'essa una f(x)...
era quello che volevo, ma non mi ero spiegato bene. Comunque se avrai tempo, quando scriverò la soluzione preferirei i tre disegni con una curva crescente qualsiasi. (scusa)
Ecco la figura che mi richiedevi... come vedi vale sempre la stessa relazione... dato il rettangolo una volta si somma e una si toglie.... Ma questo può essere fatto solo perché la linea è mediana, altrimenti i due rettangoli non sarebbero uguali!
perfetto, adesso siamo a posto
grazie
grazie a te!!!!
Sono riuscito a leggerlo ora Fabrizio. Grazie, così è molto più comprensibile.
Per sintetizzare il tutto con una sola figura...
Andando sia a sinistra che a destra della linea mediana, le due parti verdi rimangono inalterate e ciò che comanda è la parte azzurra che si somma sempre ...
e con questo concludo...
guardando questa figura temo che siamo arrivati allo stesso risultato.. O quasi
perché temi Umberto? Essere arrivati indipendentemente alla stessa soluzione geometrica direi che è ottima cosa... E' ovvio che quella di Arturo è la più rigorosa e classica, ma si chiedeva qualcosa senza integrali... e ormai la regola è stata trovata e in modo quasi banale (e più che sufficiente).
temo voleva dire ho paura che.. Non c entra Arturo. la mia soluzione che fra l altro richiama Mauro Maurizio Leandro é simile alla tua. Ma lo é diventata nell ultimo disegno. Poi vedrai.