Un quiz..rilassante.
Un quiz non troppo difficile , ma nemmeno troppo facile. In ogni caso spero sia rilassante. Sono però sicuro che verranno fuori in ogni caso discorsi interessanti.
Vogliamo trovare tutte le coppie di interi positivi (x,y) tali che:
Chiaramente sono ammessi tutti i metodi . Non è richiesta poi alcuna conoscenza particolare.






37 commenti
dunque... semplicissimo!
Scrivo un programmino (forse ne sarei ancora capace...) che fissa la x e fa variare la y. Poi cambia la x e via di nuovo con la y. La non troppo complicata relazione da verificare è:
y + x = xy/6
C'è bisogno che faccia variare x e y fino a infinito o quantomeno a miliardi di miliardi (tanto lo farebbe il computer)? Direi di no, dato che sommando due numeri di tre cifre otterrei un risultato già incompatibile con il prodotto dei due numeri (anche se diviso per 6). Posso perciò limitarmi a far variare x e y tra 1 (posso escludere lo zero) fino a 1000. Magari riuscirei a scriverlo col vecchio fortran... ma devo dire di essere soddisfatto? No, non lo sarei proprio e vado in cerca di una soluzione geometrica...


a ognuno il suo metodo! Come dice il testo del quiz. Io invece sono fissato con l algebra.
nel quiz precedente un programma andava bene e adesso non più... Dove sta la differenza? Ma sì, ma sì... un po' di algebra e di ragionamento va sempre bene... ma quando dico sempre, dico sempre... o dipende da altri fattori?
ribadisco quello che ho scritto nel testo: Sono ammessi tutti i metodi.
Siamo seri... basta ricavare una semplice funzione y = f(x)
Che siano queste ?
x ( 7 8 9 10 12 15 18 24 42 )
y ( 42 24 18 15 12 10 9 8 7 )
a parte il fatto che chiaramente non posso rispondere, andrebbero scritte come coppia (x,y) Maurizio altrimenti non si capisce bene. Poi chiaramente bisogna specificare il metodo usato per trovarle.
le coppie nella notazione richiesta sono queste :
(7,42) (8,24) ( 9,18) ( 10,15) (12,12) (15,10) ( 18,9) (24,8) (42,7)
Ovvia la simmetria attorno alla coppia (12,12)
Metodo usato ? Dato che il quiz invitava al rilassamento, ho ricavato y in funzione di x e poi, con excel ....
Potrebbero esserci altre coppie ? A sensazione direi di no. Intanto su questi risultati si possono già fare interessanti considerazioni che però lascio ad altri. Tutti hanno il diritto di rilassarsi.
ok intanto grazie mille Maurizio. Vediamo quanti metodi diversi vengono fuori. Sempre all insegna del rilassamento naturalmente!
in ogni caso non sottovalutate questo quiz che è si semplice ma può essere risolto in modo raffinato. Lo so, ricaviamo y in funzione di x sostituiamo i valori e poi vediamo quali valori sono interi. Ma qualcuno mi ha insegnato che in qualche prestigiosa università non badavano solo alla soluzione ma anche a come era stata trovata. Ciò è stato ribadito anche recentemente. Cerchiamo di introdurre un metodo che ci permetta di definire un range di valori possibili e la determinazione diretta di essi.
Oh mamma mia! excel... ma lo studio di funzioni dov'è finito? E ho cercato di spiegarlo in lungo e in largo... a cosa è servito?????
Penso di non essere più adatto al mondo di oggi e nemmeno al blog di adesso... lo posso abbandonare se questo è il nuovo stile (in questo periodo non piangerei nemmeno)
Cosa c'è di più bello e semplice e divertente di studiare la funzione:
y = 6x/(x-6) ?
Con i suoi asintoti e compagnia bella? Poi se si vuole si prendono degli interi sia positivi che negativi (chissà perché li dobbiamo trascurare?)e si risponde alla domanda. Ma diventa cosa secondaria e fine a se stessa. Il vero problemino matematico è disegnare la funzione. E, invece, vediamo quello sgorbio che trae in inganno qualsiasi lettore che vorrebbe studiare giustamente una funzione. Per x = 6, la y vale un numero finito! E sembra che la curva non passi per l'origine... e via dicendo...
No, io non ci sto più... matematica fine a se stessa non è rilassamento ma cadere nelle braccia di un programmino qualsiasi che non insegna un bel niente!
Mi dispiace, amici cari... ma così, io non vado più avanti! Se qualcuno vuole il blog se lo prenda pure....
E per concludere definitivamente... qualsiasi funzione può essere rappresentata andando avanti per punti (invece che interi possiamo mettere decimali con un dx piccolo a piacere). Chi me l'ha fatto fare a scrivere decine e decine di pagine per arrivare allo studio di una funzione? Basta chiedere a excel e pazienza se spariscono gli asintoti e i flessi e cose del genere... No, basta! Non posso più accettare questo svilimento assoluto dell'algebra e non solo. Rilassamento NON PUO' VOLER DIRE: "faccia tutto uno stupido programmino e al diavolo il significato finale..." Almeno in quello che era il "mio" blog...
La soluzione si ottiene manualmente senza dover studiare rigorosamente la funzione e senza demandare a programmi i facili calcoli da fare. Probabilmente esistono modi più raffinati e formalmente eleganti, tuttavia posso dire che ...
1/x + 1/y = 1/6 può essere scritto come 1/12 + 1/12 = 1/6 (significa x=y =12 ) coppia (12,12)
diminuendo progressivamente il denominatore del primo termine ( ossia la x ) di 1 avrò sempre valori di x interi e ricavando y posso verificare se anche questo valore è intero. Infatti 1/y = 1/6 - 1/x ossia y = 6x/(x-6).
1/11 +1/y = 1/6 ricavo y = 66/5 non è intero
1/10 + 1/y = 1/6 y = 60/4 = 15 coppia (10,15)
1/9 +1/y = 1/ 6 y = 54/3 = 18 coppia (9,18)
1/8 + 1/y = 1/6 y = 48 /2 =24 coppia (8,24)
1/7 +1/y =1/6 y = 42/ 1 = 42 coppia (7,42)
A questo punto, assegnando a x il valore 6, avremmo uno zero al denominatore della y.
Se poi scendessimo ulteriormente con la x avremmo valori di y negativi, non richiesti.
Le coppie trovate sono quindi 5 a cui vanno aggiunte altre 4 coppie ottenute invertendo x e y laddove i valori di x e y sono diversi.
Studiando la funzione salta subito all'occhio che 7 e 42 sono i limiti, dato che c'è un asintoto per x= 6 e y = 6...
Basta poi spostare gli assi per avere y=36/x, una bella iperbole con tutto quello che segue... I limiti diventano, ovviamente 1 e 36. E basterebbe scomporre 36 per avere subito i risultati interi.
Mi spiace, ma excel è proprio una scelta modernamente moderna, ma del tutto insipida... almeno in questo caso...
I risultati interi che si ottengono scomponendo il 36 vanno arricchiti (per via della traslazione eseguita) in modo da ottenere le coppie (7,42) e (10,15) con le loro simmetriche.
y = 36/x
y = 2 2 3 3/x
x = 1, 2, 3, 4, 6, 9, 12, 18, 36
basta poi aggiungere 6... caro excel, quanti calcoli inutili...
Invito caldamente a formulare i quiz (meglio diminuirli comunque se non escluderli del tutto) in modo che la soluzione sia legata alla logica e alla valutazione dell'importanza matematica o geometrica o fisica. Risolvere una funzione per punti dovrebbe essere cosa assurda per questo blog, almeno fino a che ci sarà il mio nome. Se non in casi più che necessari... Ma questo non lo era certamente...
A me sembra proprio di no... 36 + 6 = 42 e 9 + 6 = 15
Mi sento in obbligo, per i lettori meno esperti, di esplicitare meglio il ragionamento basato sullo studio di una funzione.
La relazione di partenza equivale a dire:
y = 6x/(x-6)
si potrebbe studiare questa curva e vedere subito i suoi asintoti orizzontali e verticali.
Ancora meglio è, però, fare una trasformazione di coordinate e porre:
X = x - 6
Y = y - 6
si ottiene, sostituendo:
Y + 6 = 6(X + 6)/(X + 6 - 6) = (6X + 36)/X
XY + 6X = 6X + 36
XY = 36
Y = 36/X
Y = 3 3 2 2/X
Le possibili X sono quelle che dividono esattamente il numeratore dando un numero intero come risultato:
X = 1, 2, 3, 4,6, 9, 12, 18, 36
da cui
Y =36, 18, 12, 9, 6, 4, 3, 2, 1
Basta poi fare
x = X + 6
y = Y + 6
per avere le coppie richieste...
Ma, intanto, è quasi obbligatorio calcolare gli asintoti, fare qualche limite destro e sinistro e capire con che funzione abbiamo a che fare. Infine, come divertimento puro (o rilassamento) si possono facilmente trovare le coppie richieste che sono sicuramente le SOLE positive (excel non dava certezza) per la stessa definizione di iperbole.
Buon divertimento, ma intelligente e istruttivo, sempre e comunque. Qualsiasi quiz deve servire per imparare o ripassare qualcosa, non certo solo per rispondere... altrimenti viva Celestia!


mi sembra che anche il tuo ultimo quiz sia stato formulato male allora, visto che anche li é stato usato Excel. Io non sono una persona autoritaria, quindi ho lasciato la più ampia libertà di soluzione. Quella frase te la potevi anche risparmiare. Il fatto poi che abbia avuto una soluzione logica matematica prova proprio il contrario.
e mi sembra che anche in quel caso avevo detto le stesse cose... anche se il problema era molto meno risolvibile con la pura logica, come questo. Il fatto che tu possa lasciare libera la scelta non mi sta per niente bene. Se io facessi un quiz in cui chiedo di ricavare la massa della terra a partire da certi dati e uno mi rispondesse andando a vedere il risultato su celestia, sarebbe ammesso? No, non servirebbe a niente e così è lasciare la libertà di andare per punti. E'una questione di divulgazione istruttiva. Non facciamo le gare, ma cerchiamo di insegnare a ragionare e a riflettere su cosa si è imparato. Forse non sono riuscito a far comprendere lo spirito del blog. Colpa mia, ma ho cercato di dirlo in tutti i modi possibili.
Se poi questo vuol dire essere autoritario... lascio che siano i lettori a dirmi di smettere...
Cari amici, da me ci sono 35 gradi e capisco che faccia caldo anche dove vi trovate voi.
Non è il caso quindi di scaldarsi ulteriormente.
Rispondo a Enzo...
Quando scrivevo che la scomposizione del 36 è la base che va arricchita per arrivare ai valori degli interi, intendevo proprio quello che hai scritto poi nel tuo commento (aggiungendo 6). Tutto OK.
Excel non disegna gli asintoti, ma nella cella segnala la divisione per zero.
Nel grafico la linea inizia da x=1 perché nei dati forniti è stato escluso il valore x = 0.
Sulla necessità di formulare i quiz spingendo il lettore a far funzionare il cervello e non il PC sono d'accordo, questa volta ci siamo presi una vacanza e sappiamo che non è la regola.
Rispondo a Umberto.
Nel quiz precedente di Vincenzo ho usato excel solo perché Arturo si era posto l'interrogativo se la cosa fosse fattibile. Non era esclusa a priori la possibilità di usare quello strumento.
Questo nuovo quiz che hai proposto con la apertura ad utilizzare qualsiasi mezzo (anche la divinazione) può dare ottimi spunti e lo vedremo di certo. Poco importa se in un commento salta fuori excel.
Io ho interpretato il quiz come un invito a fare una passeggiata con il mezzo che si vuole. Si può andare a piedi (ossia a mano - con il ragionamento) o in bicicletta ( con excel). A me sta anche bene, perché un quiz ogni tanto può essere anche di semplice evasione.
Insomma, non è il caso di prendersela. Lo dico per tutti, anche per il povero excel che potrebbe sentirsi vilipeso.
(Quasi lo disinstallo, per evitare tentazioni in futuro...)
Via, amici.. un sorriso !
non ho detto che tu sia autoritario, ho detto che non lo sono io. E secondo te cosa dovevo dire? Non usate Excel? Non usate il computer. O dire usate questo o quello? É un po' difficile. Sta alla persona capire il senso del metodo usato. Quando ho detto usate il metodo che volete mi riferivo chiaramente alla matematica in genere.
scusa, Umberto, basterebbe dire di non andare per tentativi ripetitivi, ma risolverlo con la propria testa e senza aiuti "meccanici". In questo caso ci stava benissimo. Ognuno può gestire il proprio quiz come vuole e quindi anche chiedere di ragionare e non di andare in moto al giro di Francia. Tutto lì... Non è questione autoritaria, ma di spirito del blog... Comunque fa caldo e lasciamo perdere... Mi prenderò un po' di vacanza...
mi sembrerebbe di offendere i lettori.chi segue il circolo senz altro non è Un bambino. Certe cose non riesco proprio a dirle. Visto appunto il caldo volevo solo fare un quiz leggero e rilassante. E invece guarda cosa é venuto fuori.
rilassante sì, ma escludendo soluzioni celestiali...
Direi che lo studio di un iperbole era cosa alla portata di tutti...
non serviva nemmeno l iperbole né lo studio di funzioni. Comunque vedrai.
Giusto per stemperare un po', che ne direste del grafico della funzione z= 1/x + 1/y tagliato dal piano z=1/6 ?.....
Ok, ok, decisamente piu' semplice e istruttivo lo studio della funzione y=f(x), che poi altro non e' che quella della curva intersezione tra le fue suddette entita' geometriche in 3D.
Qui oggi 32 gradi, fortunatamente in diminuzione per intervenuto amico maestrale
Grazie Arturo, stavo disegnando proprio quelle superfici, ma come sempre sei più veloce. (in più hai anche qualche grado di vantaggio)
finalmente soluzioni logiche e lucide... Ben vengano, ma non le celestiadi... Ovviamente, per fare le figure chiare l'uso di programmi computerizzati è tutta un'altra cosa. Malgrado il caldo, spero di essere stato capito...
Ovviamente, per fare le figure chiare l'uso di programmi computerizzati è tutta un'altra cosa. Malgrado il caldo, spero di essere stato capito...
se no... pazienza...
Vorrei tornare su questo mio commento precedente ..
17 luglio 2018 at 15:35
La soluzione si ottiene manualmente senza dover studiare rigorosamente la funzione e senza demandare a programmi i facili calcoli da fare. Probabilmente esistono modi più raffinati e formalmente eleganti, tuttavia posso dire che ...
1/x + 1/y = 1/6 può essere scritto come 1/12 + 1/12 = 1/6 (significa x=y =12 ) coppia (12,12)
diminuendo progressivamente il denominatore del primo termine ( ossia la x ) di 1 avrò sempre valori di x interi e ricavando y posso verificare se anche questo valore è intero. Infatti 1/y = 1/6 - 1/x ossia y = 6x/(x-6).
1/11 +1/y = 1/6 ricavo y = 66/5 non è intero
1/10 + 1/y = 1/6 y = 60/4 = 15 coppia (10,15)
1/9 +1/y = 1/ 6 y = 54/3 = 18 coppia (9,18)
1/8 + 1/y = 1/6 y = 48 /2 =24 coppia (8,24)
1/7 +1/y =1/6 y = 42/ 1 = 42 coppia (7,42)
A questo punto, assegnando a x il valore 6, avremmo uno zero al denominatore della y.
Se poi scendessimo ulteriormente con la x avremmo valori di y negativi, non richiesti.
Le coppie trovate sono quindi 5 a cui vanno aggiunte altre 4 coppie ottenute invertendo x e y laddove i valori di x e y sono diversi.
Questo approccio parte da una evidenza lampante ( 1/6 = 1/12 +1/12) e opera solo sui numeri interi inferiori al 12, fino a giungere al limite a cui si annulla il denominatore e poi diventa negativo.
I calcoli , rigorosamente a mano, riguardano solo 5 valori e generano tutti i risultati ottenibili. In altri termini non ci sono calcoli "inutili".
Mi sembra un metodo veloce e sicuro, comprensibile a tutti e basato su un ragionamento logico.
ti dico solo una cosa Maurizio; questo tipo di equazioni si chiamano diofantee e venivano risolte con metodi e trucchi . Al tempo non conoscevano le funzioni. Uno può anche usarle, ma allora..
Ho trovato 10 coppie di interi positivi che soddisfano la relazione proposta da Umberto. Poichè c'è una simmetria tra x e y le coppie (x,y) "originali" sono 5: (12,12), (10,15), (9,18), (8,24) e (7,42). Le altre 5 si ottengono scambiando i due valori.
Il metodo che ho utilizzato è piuttosto ingarbugliato, ma finora è questo quello che ho trovato.
Riscrivo la relazione come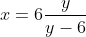 . x è intera se
. x è intera se 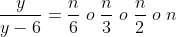 dove n è un intero.
dove n è un intero.
Parto con la prima possibilità. Risolvo l'equazione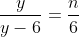 ottenedo
ottenedo 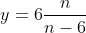 .
.
L'altro elemento è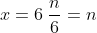
Affinché y sia intera n può avere solo alcuni valori tali che n-6 sia 6 o un sottomultiplo di 6. A questi valori di n corrispondono altrettante coppie di (x,y)
Proseguo con la seconda possibilità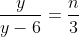 , che significa avere
, che significa avere 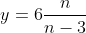 e x=2n
e x=2n
Anche qui, affinché y sia intera n può avere solo alcuni valori ai quali corrispondono altrettante coppie di (x,y)
Tra questi valori solo il secondo non era già tra i 4 precedenti, considerando anche lo scambio tra x ed y.
Si potrebbe continuare con le altre possibilità, ma si ottengono solo coppie già presenti tra quelle già trovate.
ok Fabrizio grazie. Sarà anche ingarbugliato ma è un metodo originale e diverso dagli altri
Non conoscendo le funzioni occorre trovare un modo per aggirare l'ostacolo. Forse seguendo questo ragionamento...
Considero intuitiva la seguente relazione:
1/12 + 1/12 = 1/6 da cui ho subito la prima coppia (12,12)
Ora riscrivo l'espressione in questo modo: 1/6 * a + 1/6 * b = 1/6 ove a+b = 1
Il primo termine corrisponde a 1/x e il secondo termine a 1/y
dato che 1/6 * 6/x = 1/x ne deriva che a = 6/x e quindi: b= 1- 6/x
In termini generali ho questa uguaglianza:
1/6 * 6/x + 1/6 *(1- 6/x) = 1/6
Sostituisco progressivamente a x i valori interi, positivi, decrescenti a partire da 11.
Tutte queste espressioni valgono 1/6.
Ricordo che la x è l'inverso del primo termine e la y è l'inverso del secondo termine.
1/6 * 6/11 + 1/6*(1-6/11) = 1/6 x=11 ; y=66/5 non intero
1/6 * 6/10 + 1/6*(1-6/10) =1/6 x=10; y=60/4 intero = 15
1/6 * 6/9 + 1/6 *(1-6/9) = 1/6 x= 9; y=54/3 intero = 18
1/6 * 6/8 + 1/6 *(1-6/8) = 1/6 x= 8; y=48/2 intero = 24
1/6 * 6/7 + 1/6 *(1-6/7) = 1/6 x =7; y=42/1 intero = 42
Scendendo sotto x = 7 troviamo:
1/6 * 6/6 + 1/6 *(1- 6/6) = 1/6 x=6 ; y= infinito non valido
1/6 * 6/5 + 1/6 *(1 - 6/5) = 1/6 x=5; y=negativo non valido
eccetera...
In conclusione le coppie trovate , oltre alla prima (12,12), sono;
(10,15) ( 9,18) (8,48) (7,42) e le loro simmetriche, scambiando x e y:
(15,10) (18,9) (48,8) (42,7)
Sarà abbastanza "truccato" ?
Un altro modo per trovare le nostre coppie di valori può essere questo.
L'obiettivo è sempre quello di evitare di andare per tentativi, anche se mirati.
Riscrivo la relazione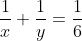 come
come 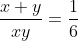 . Quindi se
. Quindi se 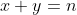 , allora
, allora 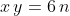 .
.
Da queste due equazioni elimino la y ed ottengo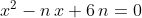 . Ricavo la n ed ottengo:
. Ricavo la n ed ottengo:
Quindi se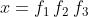 , dove le f sono i tre tipi di fattori elencati sopra,
, dove le f sono i tre tipi di fattori elencati sopra,
allora se in x-6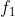 è preso due volte,
è preso due volte, 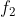 è preso una volta e
è preso una volta e 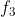 non è prese
non è prese
Quindi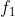 ed
ed 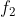 devono essere fattori di 6. Da questi si ricava
devono essere fattori di 6. Da questi si ricava 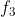 e dai tre fattori si ricava x come
e dai tre fattori si ricava x come
I 9 possibili casi sono riassunti in questa tabella
scusa Fabrizio ho già pubblicato la soluzione senza accorgermi del tuo ulteriore commento. Se vuoi aggiungere qualcosa puoi farlo lì