Quiz: il ritorno dell'ubriaco.
Ricordate il nostra simpatico ubriaco alle prese con le chiavi del portone? Ebbene adesso il nostro amico sta affrontando un impresa ben più difficile: uscire sano e salvo da un Hotel in cui si è intrufolato per ubriacarsi gratuitamente.

Fingendosi un cliente e quindi con addebito sul conto della camera di qualche sventurato, egli passa parecchio tempo al bar dell' Hotel ubriacandosi stavolta in modo molto serio, da coma etilico. Infatti abituato al vino, non regge i cocktail, che lo sballano quasi subito.

A un certo punto capisce però che è giunto il momento di sparire, quindi imbocca il corridoio C della figura sottostante:
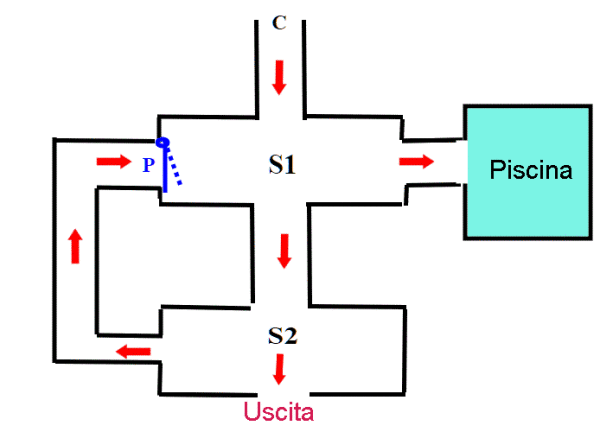
Le direzioni possibili sono quelle delle frecce rosse: per uscire l'ubriaco deve attraversare le due stanze di attesa S1 e S2 andando sempre diritto. Ma visto lo stato comatoso, possiamo considerare il suo cammino puramente aleatorio.
Giunto in S1, egli può andare dritto, oppure girare a sinistra verso la piscina, finendoci dentro e affogando.Non può girare a destra, perchè la porta P può aprirsi solo dall'esterno. La probabilità di andare dritto o girare è la stessa, ed è uguale ad 1/2. Se poi riesce ad arrivare in S2, può trovare subito l'uscita, oppure girare a destra e tornare indietro (sempre con le stesse probabilità di scelta, 1/2) e tornare in S1, spingendo la porta P apribile solo dall'esterno di S1. La domanda del quiz è:
qual'è la probabilità che il nostro amico guadagni l'uscita sano e salvo? E' possibile inoltre che esso continui a girare all'infinito per S1 ed S2 passando per la porta P e non trovando mai l'uscita ?






8 commenti
In S1 50 piscina, 50 prosegue.
In S2 25 salvo, 25 ritorno S1.
Si ripete e si somma come foto
La probabilità che si salvi è del 33,3333
ok Gianfranco grazie. Poi spiegherai meglio il tuo ragionamento che è un po' ermetico. Intanto aspettiamo anche gli altri
La probabilità p data dal rapporto fra i “casi favorevoli” e i “casi possibili”.
Al primo passaggio, in S1 casi possibili = 2, casi favorevoli uscita = 1, p = 1/2
In S2 il rapporto si riduce, di nuovo due casi possibili e uno solo favorevole p = 1/4
A intuito, se si ritorna in S1 il ciclo si ripete facendo aumentare il valore p = 1/4 + 1/(4*4) + 1/(4*4*4) + 1/(4*4*4*4) + 1/ecc. = 1/3 . Ogni volta che si arriva in S1 o S2 è come si facesse testa o croce con una moneta.
La possibilità che esca sempre testa (porta a destra) diminuisce ad ogni tentativo.
1/(4*4*4*4*4*ecc…..) la probabilità p che continui a girare 1/(4^n) con n numero ripetizioni.
ok Gianfranco, non stai dicendo cose errate. Mi piacerebbe però fare uno schema del problema in modo grafico per poterci ragionare meglio. Quello che in linguaggio tecnico si chiama proprio "grafo".
Giancarlo ha detto la sua; possono farlo anche gli esperti. Il quiz è aperto a tutti.
Partendo dalla sala S1 ci sono 3 esiti possibili per l’ubriaco:
1) finisce in piscina il 50% delle volte
2) trova l’uscita il 25% delle volte
3) si ritrova nuovamente nella sala S1 passando per la porta P il 25% delle volte, e riprende il ciclo.
In ciascuno dei giri che fa partendo da S1, la probabilità di finire a bagno in piscina (B) è il doppio di quella di trovare l’uscita (U). Cioè B=2 U, indipendentemente da quanti giri possa avere completato.
Per utilizzare questa relazione occorre rispondere alla seconda domanda di Umberto: “E' possibile inoltre che esso continui a girare all'infinito per S1 ed S2 passando per la porta P e non trovando mai l'uscita ?”
La mia risposta è no. Se un evento è possibile presto o tardi accade. E qui ci sono 2 eventi che fanno uscire l’ubriaco dal giro ed Umberto ha usato la parola infinito. Ovviamente, supponendo che non sia fermato dalla sicurezza dell’albergo o non crolli.
Questo si traduce in un vincolo sulla somma: U+B=1, non essendoci altre possibilità.
Se B=2 U come visto sopra, allora U+2 U=1. U deve quindi essere 1/3, come ha già trovato Gianfranco per altra via.
Una considerazione sulla seconda domanda di Umberto. Come ho detto, la risposta alla domanda come formulata credo sia: no, non è possibile che continui a girare all'infinito per S1 ed S2 ripassando per la porta P. Ma se la domanda fosse formulata in modo diverso: “Dopo quanto tempo puoi escludere di ritrovare il nostro ubriaco vagare tra le sale dell’albergo?” A questa domanda non si può dare una risposta certa. Anche dopo tempi lunghi non è possibile escludere totalmente di ritrovare il nostro ubriaco ancora vagare tra S1 ed S2. Comunque più passa il tempo e più questa probabilità diminuisce e si avvicina allo 0. Questo conferma la mia risposta alla domanda traguardata all’infinito.
perfetto Fabrizio
Bisognerebbe adesso trasformare il ragionamento do Gianfranco usando le serie infinite per avere un risultato più compatto della prima risposta