Categorie: Matematica
Tags: calcolo minimi e massimi divisione per zero quiz soluzione grafica
Scritto da: Maurizio Bernardi
Commenti:0
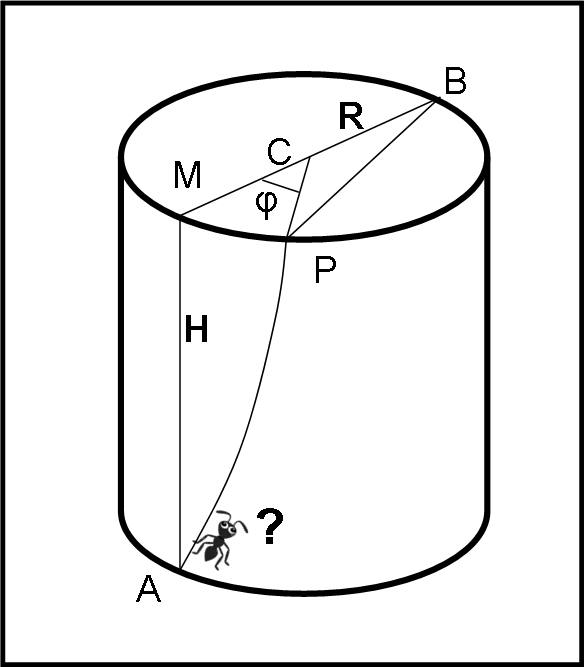
Soluzione del quiz "non è banale camminare su un cilindro"
Avevamo lasciato la nostra formica alla base del cilindro, in preda ai dubbi che le aveva instillato l'amico scarabeo.
|
|
“Stai attenta, cara amica. Tu hai preso una decisione trascurando la logica matematica. Sei arrivata a una conclusione senza valutare veramente tutte le variabili del problema. E’ un po’ come se tu avessi scelto la soluzione basandoti solo sui casi estremi, senza valutare le possibilità intermedie.” Così l'aveva ammonita, guardandola da sopra i suoi occhialini da presbite (o forse erano multifocali... mah). Ebbene la formica non è una che si tira indietro. Occorre studiare tutte le possibili alternative? Benissimo, e che sarà mai ? |
Per prima cosa prova a cercare una via esclusivamente analitica per dimostrare che il punto di nullo della derivata prima, quando esiste, corrisponde ad un punto di massimo della funzione “percorsomisto(φ), ma si rende conto subito che la cosa non è poi così banale.
Allora prova a sviluppare in serie il sen(φ) ma, avendo a che fare con la maledetta radice quadrata che compare dall'altra parte (non a caso le sono invise le radici), anche fermandosi solo al terzo termine della serie, le viene già un'equazione di sesto grado.
Morale della favola, l'unica alternativa che rimane è quella grafica.
Ed ecco che con l'aiuto di Arturo, deus ex machina di Geogebra, trova la risposta nel grafico della funzione e della sua derivata , raffigurate qui sotto per un possibile valore di K=0,84
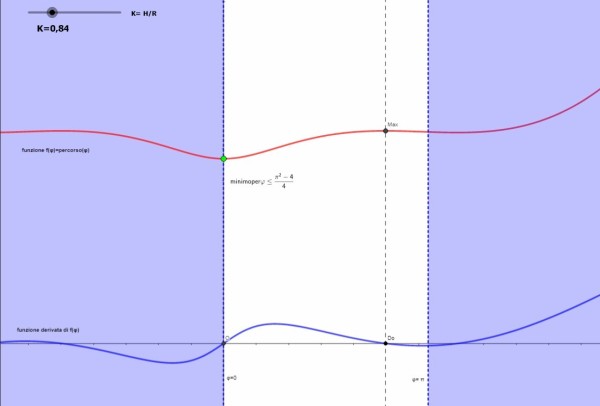
La linea superiore ROSSA rappresenta il valore di distanza tra A e B , al variare dell'angolo φ data dalla equazione del percorso misto, che passa per il punto P:
La linea BLU rappresenta l'equazione della sua derivata:
che, come si nota facilmente, si azzera nei due punti di ascissa φ = 0 e φ = D0 , intersecando l'asse orizzontale.
Nel primo punto per φ=0 si ha un minimo, nel secondo punto φ=D0 si ha un massimo.
Restando nell'intervallo φ ( 0 , π ), da questo punto in poi, la funzione diminuisce ma, arrivata in corrispondenza di φ = π , il suo valore resta comunque al di sopra del minimo.
Il percorso più breve sarà costituito da una salita verticale lungo il cilindro da A al punto P , lungo perpendicolare, e successivamente dal tragitto , lungo il diametro della circonferenza, da P fino a B.
Ora, per vedere la situazione in un caso generico, per un qualsiasi valore di K, basta seguire questo link che apre la finestra del grafico dinamico e, potendo variare con il comando lineare il rapporto k = H/R, constatare che all'interno dell' intervallo tra 0 e π, in corrispondenza dell'eventuale punto di nullo della derivata, si presenta sempre un massimo della funzione, quindi il percorso misto , per quel valore di k, non è minimo.
Solo nel caso in cui il rapporto K= H/R valesse 1,467 il valore minimo della funzione , pari a 2,362, si presenterebbe , oltre che per φ = 0 anche in corrispondenza dell'angolo massimo φ = π.
Sarebbe indifferente allora , come già spiegato nel quiz, seguire uno o l'altro dei due cammini.
Per rapporti K= H/R superiori a 1,467 non resta che seguire il cammino che porta direttamente dal punto A al punto B.
Adesso anche lo scarabeo non avrà più niente da dire.
Bellezza, Verità e Buon Senso
(divagazioni di Oreste Pautasso)
Si dice che Albert Einstein avesse dato poca importanza alla notizia che la sua teoria fosse stata verificata sperimentalmente.
Quando gli venne chiesto che cosa avrebbe pensato nel caso contrario, egli rispose: “Sarei rimasto dispiaciuto per Dio. La teoria è corretta”. Ciò che lo rese talmente sicuro nel dare il suo giudizio era l’estrema eleganza delle equazioni: come poteva essere sbagliato un sistema matematico così bello?
Eh sì, Quando si vede una formula un po' complicata la prima cosa che si pensa è di lavorarci sopra per renderla semplice, il più semplice possibile.
“Piccolo è bello”, era il titolo di un famoso libro di Economia dei primi anni 70, di Ernest Shumacher, con il sottotitolo: “uno studio di economia come se la gente contasse”, a cui fa da controaltare lo slogan “Grande è meglio” del mondo globalizzato.
Ma tornando alle formule... più sono eleganti e sintetiche, più promettono di funzionare.
Facciamo un esempio.
Una funzione di φ ha questa formula:
ove H e R sono due costanti > 0
ne vogliamo studiare la derivata y' = dy/d φ, rappresentandola graficamente e valutando i punti in cui si annulla, a cui corrisponderanno valori minimi o massimi della funzione y.
Questa è la formula della sua derivata:
Basta uno sguardo superficiale per capire che per φ = 0 si avrà y'=0 ( vediamo di ricordarlo.)
A questo punto scatta l'ansia per la bellezza. Pettiniamo e acconciamo il meglio possibile la formula cosicché da renderla presentabile in società, snella ed elegante.
Il percorso della bellezza è sempre un po' tortuoso e sofferto “ per apparire bisogna soffrire” o se preferite, in inglese... “no pain, no gain”. Insomma, lo dicono tutti che è così.
Allora soffriamo un po' e manipoliamo la nostra formula fino all'estremo raggiungibile...
lo pongo = 0 e separo i due termini, così:
divido ambo i membri per R e li moltiplico per
)
elevo tutto al quadrato
sostituisco
con
divido ambo i membri per R2
sviluppo e riorganizzo
sostituisco al rapporto H/R il simbolo K e semplifico
porto a sinistra K2
raccolgo sui quadrati di K e φ
moltiplico tutto per -1 e ricavo K2
Al termine di questa gimkana, siamo un po' stremati ma molto felici di vedere un risultato con una simmetria che riluce di bellezza, una luciferina bellezza che ci garantisce anche la Verità.
Però... però se mettiamo φ=0...
Prima di fare i grafici dobbiamo capire meglio se in tanta bellezza si cela altrettanta verità. E' a questo punto che entra in gioco il Buonsenso.
Ahi ahi, signora Longari … Se φ=0 abbiamo uno Zero al denominatore !
Una tragedia..
Dividere per zero... non si può, non si deve. E’ lo spregevole trucco con cui si arriva a dimostrare che 1=2 e altre nefandezze del genere. Lo vedete QUI (andate a fidarvi dei Professori...)
Avemmo dovuto fermarci prima.
Insomma, cerchiamo di migliorare la bellezza senza perdere di vista il buon senso.
Per le formule , come per le persone, bellezza e sincerità sono variabili indipendenti, non necessariamente correlate, Einstein permettendo.
Zero e misfatti
(incursioni non autorizzate di Maurizio Bernardi)
Quando mio figlio Andrea aveva pochi anni, uno dei quesiti più destabilizzanti che poneva, ad ogni lancio di dadi, riguardava il conteggio delle caselle di cui avanzare sul tabellone del Gioco dell'Oca: “Papà, se devo fare 3 passi, la casella in cui si trova l'omino la devo contare come 1?”

E' così che ho dovuto presentargli lo zero, spiegando che il primo passo è quello che lo porta nella casella UNO e, non avendo fatto passi in precedenza, il numero da associare alla casella in cui si trova inizialmente è ZERO (insomma, il primo assioma di Peano: “zero è un numero naturale” e il terzo: “zero non è preceduto da alcun numero”).
Credo che, ancora oggi, ogni tanto ci ripensi, però non mi chiede più niente.
Solo pochi giorni fa ho sentito per caso mio nipote Marco che gli faceva esattamente la stessa domanda. Il DNA non perdona, è lo strumento più affilato della Nemesi.
Molto tempo prima, un paio di millenni fa, i Maya utilizzavano lo zero nel loro sistema vigesimale (contavano con le dita delle mani e anche dei piedi). Se lo erano dovuto inventare per poter rappresentare una posizione separatrice, uno spazio vuoto nei loro calendari.
La rappresentazione simbolica era piuttosto varia: una conchiglia, una spirale, un occhio, insomma c'era già una certa libertà di scrittura, come quella che vediamo oggi con twitter e facebook.
Anche i babilonesi, tre secoli prima di Cristo, rappresentavano uno spazio vuoto con un particolare simbolo (due cunei inclinati), che però esprimeva solo l'idea della assenza, ma non era coinvolto nelle operazioni numeriche.
Solo dopo il 600 gli Indù, che erano entrati in contatto con i Greci fin dai tempi di Alessandro Magno, iniziarono a considerare questo simbolo come un numero e ad utilizzarlo nel sistema di rappresentazione posizionale. Dagli Indiani, attraverso gli Arabi, attorno all'ottavo secolo, il sistema di numerazione posizionale è arrivato anche a noi. Fino ad allora il gioco dell'oca non si poteva utilizzare.
Se aggiungo zero a un numero non cambia nulla. Un matematico preferisce dire che “lo zero è l'elemento neutro per l'addizione”. E va bene, si sa che sono fatti così...
Se moltiplico per zero un numero lo annullo, cioè il risultato è zero.
Mettendo assieme le due cose, il matematico riesce a dimostrare che di zeri ce n'è uno solo (meno male, altrimenti sarebbe una tragedia).
A questo punto ci nasce la curiosità di sapere cosa succede quando un numero viene diviso per zero.
Ai tempi dei primi matematici indiani, le idee in proposito erano piuttosto variegate.
Secondo Brahmagupta, eminente astronomo vissuto nel 600 dopo Cristo, dividere 0 per se stesso darebbe come risultato 0. Inoltre, dividendo 1 per 0 si ottiene infinito.
Di parere diverso è, un paio di secoli dopo, Mahavira, un altro matematico indiano che, nel suo manuale di Matematica, spiega che un numero non viene modificato, quando è diviso per zero.
Quindi, secondo lui, 1 diviso 0 resta 1. Filosoficamente parlando: se non c'è nessuno a dividersi la torta, la torta rimane tale e quale, una visione molto materialista, per un indiano.
Di parere opposto, nel XII secolo, Bhaskara un altro astronomo e matematico che oltre ad affermare che “dividendo infinito per un numero, resta infinito” ( cosa non così incredibile), ribadì il fatto che un numero diviso per zero è infinito (in questo caso la torta indivisa diventa enorme).
E i Nostri? Cosa ne pensano?
Con una certa astuzia assegnano allo zero un risultato “indefinito”. Meglio astenersene...
Uno dei primi a dirlo, a metà del '700 fu un vescovo irlandese, Berkeley, (da cui prese il nome la famosa università californiana). Berkeley, uno dei tre empiristi britannici, assieme a Locke e Hume, nella sua opera The Analist, esprimendo la sua critica al calcolo infinitesimale, dichiarò l'impossibilità di assegnare un risultato alla divisione per zero.
Sul piano pratico è evidente che, dato che la divisione è l'operazione inversa della moltiplicazione, 17: 0 non può fare 17, perché 17x0 non fa 17.
Analogamente 17:0 non può fare 0, perché 0x0 non fa 17.
Ora è chiaro perché, in Excel, se eseguite una divisione per 0 salta fuori #DIV/0! Dove il punto esclamativo non significa “fattoriale” ma rappresenta una espressione di sdegnata meraviglia per la vostra incompetenza.
Detto tutto questo, venendo alla funzione descritta da Oreste nella sua divagazione più sopra, è chiaro che il passaggio in cui si divide per l'espressione (1-cos(φ )) è un passo fatale.
Ne vediamo le catastrofiche conseguenze in questo grafico che (per R=1, H=2 ,φ=x ) riporta la funzione iniziale, il passaggio intermedio che precede il momento della divisione per zero e il risultato dopo la divisione.
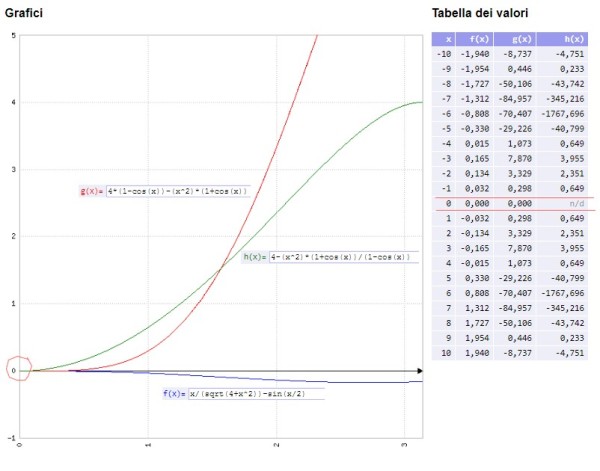
La funzione originale f(x) (curva blu in basso) taglia l'asse delle x proprio nell'origine, come vedete nella tabella in cui appare, alla riga x=0, il valore f(x) = 0,000.
Rielaborando la formula si ottiene la funzione G(x) (curva in rosso) che in corrispondenza di x=0 continua a presentare in tabella il valore g(x)=0, come deve essere.
A questo punto, eseguendo la divisione per (1-cos(x)) arriviamo alla funzione h(x) (curva verde) e alla ascissa x=0 nasce il problema: come si vede nella tabella dei valori, (n/d = non disponibile) non esiste alcun numero possibile per rappresentare l'ordinata della curva verde.
In conclusione la divisione per zero ci ha fatto perdere l'informazione che la funzione di partenza ha uno zero nell'origine degli assi.
Ecco perché l'amico Oreste si lamenta e fa appello al buon senso. Come dargli torto?